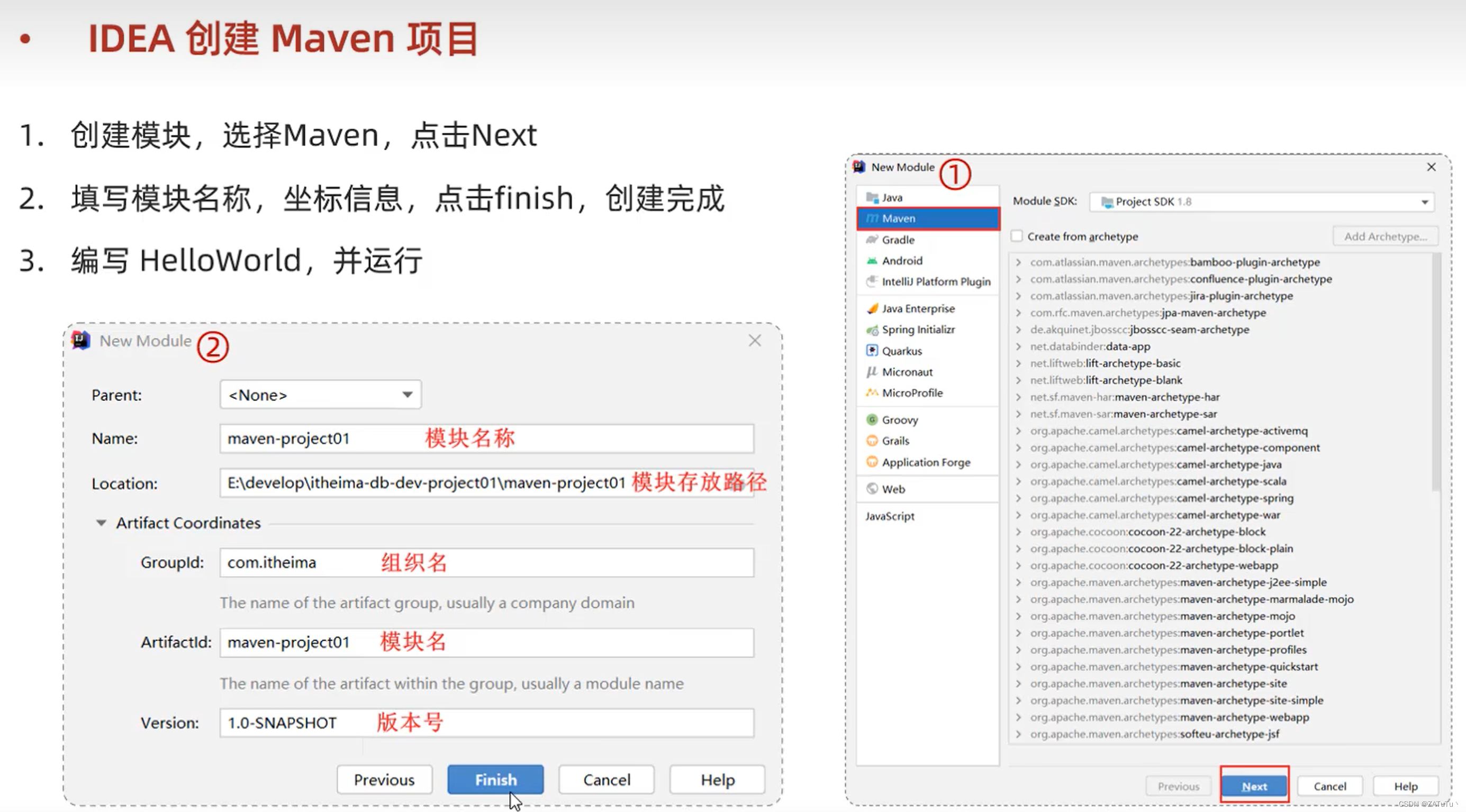
动态规划(基础)
一,背包问题
老规矩,上链接(http://t.csdn.cn/hEwvu)
(1)01背包问题
给定一个承重量为C的背包,n个重量分别为w1,w2,...,wn的物品,物品i放入背包能产生pi(>0)的价值(i=1,2,...,n)。每个物品要么整个放入背包,要么不放。要求找出最大价值的装包方案。
输入格式:
输入的第一行包含两个正整数n和C(1≤n≤20),第二行含n个正整数分别表示n个物品的重量,第三行含n个正整数分别表示n个物品放入背包能产生的价值。
输出格式:
在一行内输出结果,包括最大价值装包方案的价值、具体装包方案,用空格隔开。具体装包方案是n个物品的一个子集,用长度为n的0、1串表示(1表示对应物品被选中,0表示没有被选中)。如果这样的0、1串不唯一,取字典序最大的那个串。
输入样例:
4 9
2 3 4 5
3 4 5 7
输出样例:
12 1110
(注:1110 和0011都是价值最大的装包方案,取字典序最大的结果即为1110)
思想:最最经典的dp问题,画个图就明白了。
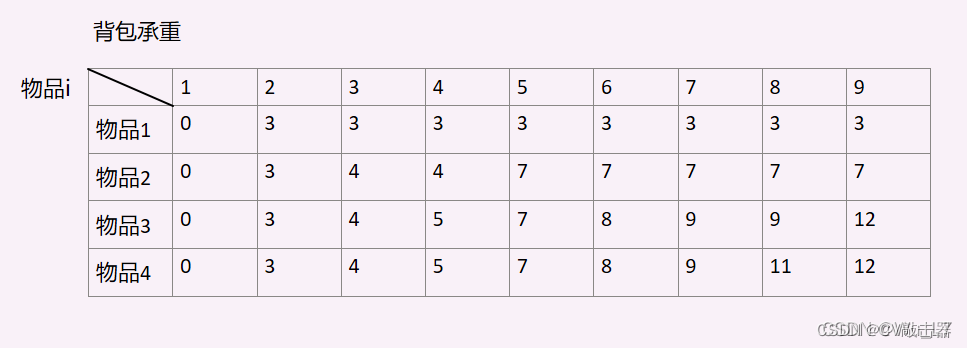
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N = 100;
int dp[N][N], w[N], val[N];int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i];//重量for (int i = 1; i <= n; i++) cin >> val[i];//价值//求最大价值for (int i = 1; i <= n; i++) {for (int j = 0; j <= m; j++) {if (j >= w[i]) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + val[i]);else dp[i][j] = dp[i - 1][j];}}cout << dp[n][m] << endl;//打印字典序for (int i = 1; i <= n; i++) {if (dp[i][m] - dp[i - 1][m] == 0) cout << "0";else cout << "1";}return 0;
}利用滚动数组优化,将二维数组降为一维数组
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int dp[N], t[N], val[N];int main()
{int time, n;cin >> time >> n;for (int i = 1; i <= n; i++) cin >> t[i] >> val[i];for (int i = 1; i <= n; i++) {//时间为j时的最大价值for (int j = time; j >= t[i]; j--) {//这里j倒序是为了防止重复拿同一件物品dp[j] = max(dp[j], dp[j - t[i]] + val[i]);}}cout << dp[time] << endl;return 0;
}(2)完全背包问题
有一个容积为 V 的背包,同时有 n 种物品,每种物品均有各自的体积 w 和价值 v,每种物品的数量均为无限个,求使用该背包最多能装的物品价值总和。
疯狂的采药 - 洛谷
思路:我们此时在多家一重循环表示同一种物品的数量就可以了,那么我们的递推式就变为
dp[i][j] = max( dp[i-1][j] , dp[i-1][ j - k*w[i] ] + k*v[i] )
AC代码
#include<iostream>
using namespace std;const int N=1005;
const int M=105;
int n,m,maxValue,temp;
int dp[M][N],t[M],v[M];int main()
{cin>>n>>m;for(int i=1;i<=m;i++) cin>>t[i]>>v[i];for(int i=1;i<=m;i++)for(int j=1;j<=n;j++){maxValue=0;for(int k=0;k*t[i]<=j;k++){temp=dp[i-1][j-k*t[i]]+k*v[i];if(temp>maxValue) maxValue=temp;}dp[i][j]=maxValue;}cout<<dp[m][n]<<endl;return 0;
}
这段代码是不能通过测试的,因为本题的数据比较大,而且我们用了三重循环,时间复杂度比较高,所以此方法不行。
同样的,我们使用滚动数组进行优化。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e7 + 5;
long long dp[N], t[N], val[N];//数据过大,开长整型int main()
{int time, n;cin >> time >> n;for (int i = 1; i <= n; i++) cin >> t[i] >> val[i];for (int i = 1; i <= n; i++) {for (int j = t[i]; j <=time; j++) {dp[j] = max(dp[j], dp[j - t[i]] + val[i]);}}cout << dp[time] << endl;return 0;
}(3)
相关文章:

动态规划(基础)
一,背包问题 老规矩,上链接(http://t.csdn.cn/hEwvu) (1)01背包问题 给定一个承重量为C的背包,n个重量分别为w1,w2,...,wn的物品,物品i放入背包能产生pi(>0)的价值(i1,…...

【Pytorch:nn.Embedding】简介以及使用方法:用于生成固定数量的具有指定维度的嵌入向量embedding vector
文章目录 1、nn.Embedding2、使用场景 1、nn.Embedding 首先我们讲解一下关于嵌入向量embedding vector的概念 1)在自然语言处理NLP领域,是将单词、短语或其他文本单位映射到一个固定长度的实数向量空间中。嵌入向量具有较低的维度,通常在几…...

动态库的命名规则
1、动态库的命名规则:libname.so.x.y.z 名字含义lib这是共享库的前缀name共享库名字x主版本号y次版本号z发布版本号 2、每个版本号的含义 版本号含义主版本号表示库的重大升级,不同主版本号的库之间是不兼容的。依赖旧的主版本号的程序需要改动相应的…...

【Linux】网络---->网络理论
网络理论 网络协议分层模型网络数据的封装于分用地址管理 网络协议分层模型 OSI五层模型:应用层,传输层,网络层,数据链路层,物理层 应用层:主要负责应用程序间的沟通,代表协议有HTML协议&#x…...
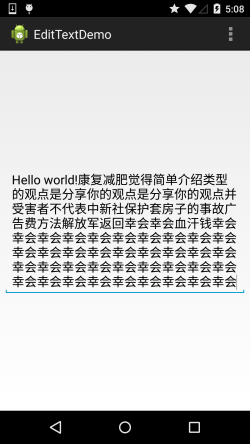
Android学习之路(4) UI控件之输入框
本节引言: 在本节中,我们来学习第二个很常用的控件EditText(输入框); 和TextView非常类似,最大的区别是:EditText可以接受用户输入! 1.设置默认提示文本 如下图,相信你对于这种用户登录的界面并…...

1.初识Web
文章目录 1. 什么是Web?2.初始Web前端2.1.Web标准 1. 什么是Web? web:全球广域网,也称万维网(www World Wide Web),能够通过浏览器访问的网站。 2.初始Web前端 网页有哪些部分组成? 文字、图片、音频、视频、超链接… 我们看到的网页&am…...
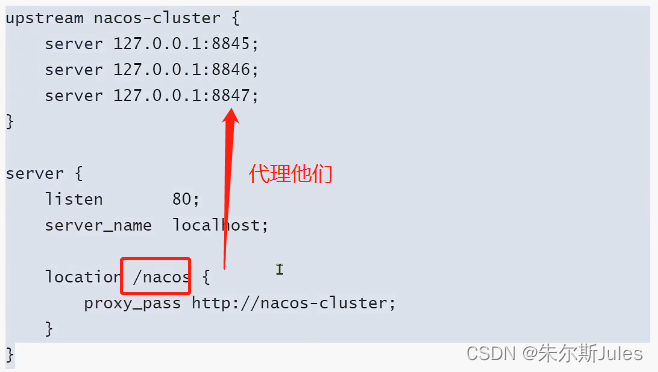
【微服务技术一】Eureka、Nacos、Ribbon(配置管理、注册中心、负载均衡)
微服务技术一 技术栈图一、注册中心Eureka概念:搭建EurekaServer服务注册服务发现(消费者对提供者的远程调用) 二、Ribbon负载均衡负载均衡的原理:LoadBalanced负载均衡的策略:IRule懒加载 三、Nacos注册中心Nacos的安…...
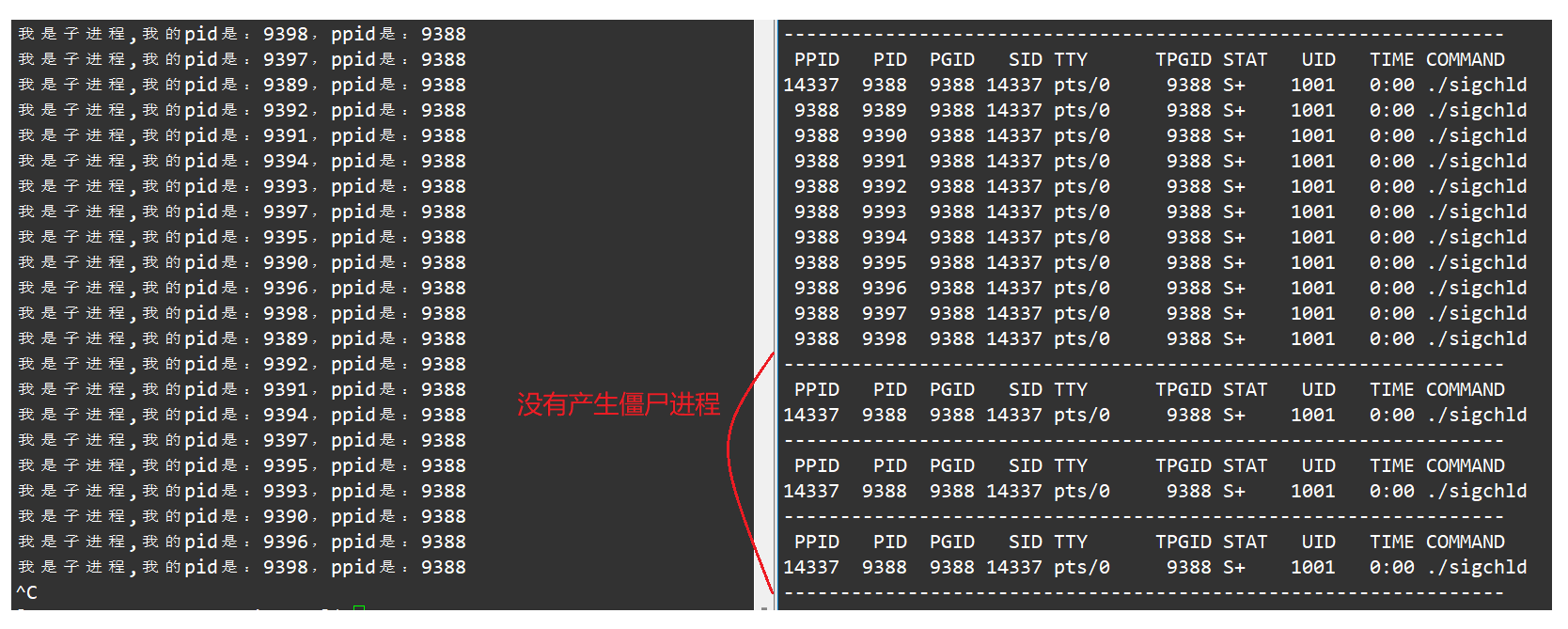
【Linux】可重入函数 volatile关键字 以及SIGCHLD信号
可重入函数 volatile关键字 以及SIGCHLD信号 一、可重入函数1、引入2、可重入函数的判断 二、volatile关键字1、引入2、关于编译器的优化的简单讨论 三、SIGCHLD信号 一、可重入函数 1、引入 我们来先看一个例子来帮助我们理解什么是可重入函数: 假设我们现在要对…...
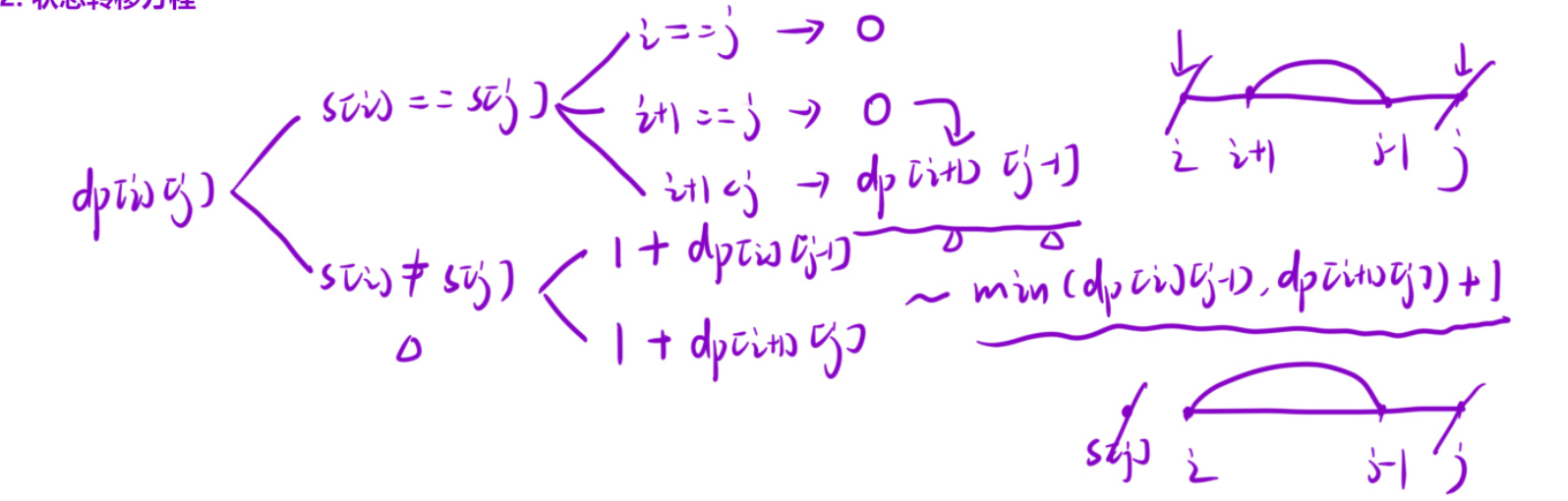
【动态规划】回文串问题
文章目录 动态规划(回文串问题)1. 回文子串2. 最长回文子串3. 回文串分割 IV4. 分割回文串 ||5. 最长回文子序列6. 让字符串成为回文串的最小插入次数 动态规划(回文串问题) 1. 回文子串 题目链接 状态表示 f[i][j]表示 i 到 j …...

Laravel Swift Mail发送带附件的邮件报错 “Swift_IoException The path cannot be empty“处理
先说下情况,就是我要做一个发送附件的邮件发送功能,结果,报错:The path cannot be empty。给我整的有点迷糊,网上也没有类似的问题。后来,我检查了一下代码,发现有个地方,是需要给附…...

Linux下常见的代理服务器软件介绍
在Linux系统中,代理服务器是我们搭建网络环境和处理网络请求的常用工具。但是,你知道Linux下常见的代理服务器软件有哪些吗?本文将为你带来对几款常见的Linux代理服务器软件的介绍,帮助你选择适合的代理服务器。 一、Squid&#…...
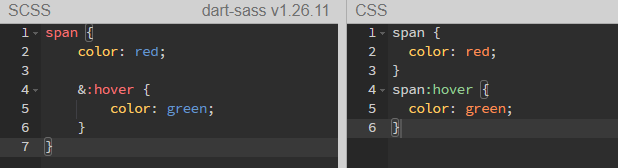
SCSS的基本用法
1、声明变量 $ 声明变量的符号 $ 下面这张图左半部分是scss的语法,右半部分是编译后的css。(整篇文章皆是如此) 2、默认变量 !default sass 的默认变量仅需要在值后面加上 !default 即可。 如果分配给变量的值后面添加了 !default 标志…...
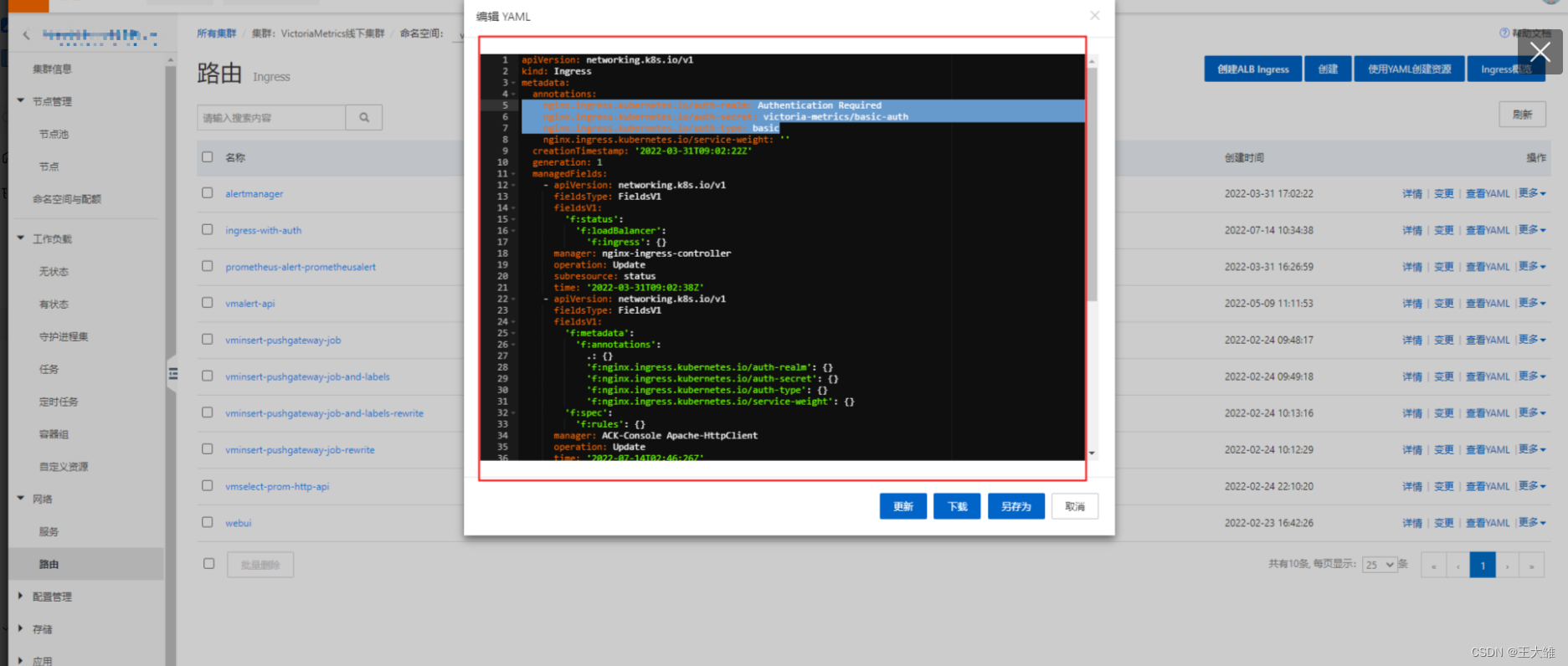
alertmanager创建nginx-ingress basic auth鉴权
步骤 生成密码 printf "admin:$(openssl passwd -crypt xxxxxx)\n" >> auth 创建新的 Kubernetes 密钥 kubectl create secret generic basic-auth --from-file auth -n victoria-metrics 修改 ingress 以使用 secret 中的凭证来实现基本身份验证 编辑 P…...
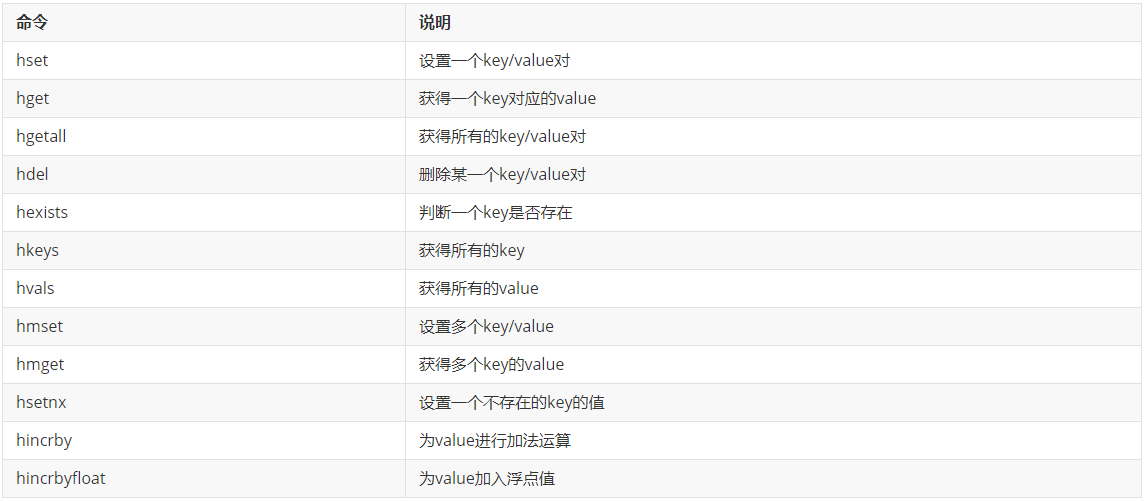
系列六、Redis中的五大数据类型及相关操作
一、五大数据类型 String类型、List类型、Set类型、ZSet类型、hash类型。 二、String类型 2.1、内存储存模型 2.2、常用操作命令 三、List类型 3.1、概述 list列表,相当于Java中的list集合。特点:元素有序 且 可以重复。 3.2、内存存储模型 3.3、常用…...
四大运营商的大流量卡测评,看完您会选哪个运营商?
很多朋友都说网上的流量卡资费是真的便宜,但是小编认为资费便宜归便宜,但是运营商的小心思也有不少。 今天小编就带大家看一看三大运营商推出的正规流量卡都有哪些小心思? 首先,移动推出的线上大流量卡数量是最少的ÿ…...
Apache-Maven
安装Maven 解压apache-maven到目录下 Maven目录如下 bin:目录中存放的是可执行文件,JAVA项目中的编译执行打包都要使用bin. conf:存放的是Maven的配置文件,本地配置、私服配置都需要在conf下的settings.xml进行配置。 lib下存放的是Maven所…...

什么是原子交换?
安全地在各个区块链网络之间传输资产对于释放被困流动性并吸引更多用户进入这一领域至关重要,同时也保持 Web3 的信任最小化核心价值。原子交换是一种让两个人在不依赖于中介来促成交易的情况下,在不同的区块链网络之间交换通证资产的方式。这为 DeFi 用…...

java springboot word文档转pdf
java springboot word文档转pdf 1、环境2、依赖3、代码 1、环境 1、java、springboot 2、maven或者gradle 3、办公软件(自己电脑上的wps或者office等,如果部署到服务器上也要安装,linux、Mac 都有,自己安装) 可能会遇…...

【Leetcode Sheet】Weekly Practice 2
Leetcode Test 1281 整数的各位积和之差(8.9) 给你一个整数 n,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。 提示: 1 < n < 10^5 【原始代码】: int subtractProductAndSum(int n){//1 < n < 10^5//…...
【BERTopic应用 03/3】:微调参数
一、说明 一般来说,BERTopic 在开箱即用的模型中工作得很好。但是,当您有数百万个数据要处理时,使用基本模型处理数据可能需要一些时间。在这篇文章中,我将向您展示如何微调BERTopic中的一些参数并比较它们的结果。让我们潜入。 二…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
