机器学习笔记值优化算法(十四)梯度下降法在凸函数上的收敛性
机器学习笔记之优化算法——梯度下降法在凸函数上的收敛性
- 引言
- 回顾:
- 收敛速度:次线性收敛
- 二次上界引理
- 梯度下降法在凸函数上的收敛性
- 收敛性定理介绍
- 证明过程
引言
本节将介绍梯度下降法在凸函数上的收敛性。
回顾:
收敛速度:次线性收敛
关于次线性收敛,分为两种判别类型: R \mathcal R R-次线性收敛与 Q \mathcal Q Q-次线性收敛。而次线性收敛的特点是:随着迭代次数的增加,相邻迭代步骤产生的目标函数结果 f ( x k ) , f ( x k + 1 ) f(x_k),f(x_{k+1}) f(xk),f(xk+1),其差异性几乎完全相同:
lim k ⇒ ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ = 1 \mathop{\lim}\limits_{k \Rightarrow \infty}\frac{||x_{k+1} - x^*||}{||x_k - x^*||} = 1 k⇒∞lim∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=1
例如:如果数值解 x k x_k xk的目标函数结果 f ( x k ) f(x_k) f(xk)与目标函数最优解 f ∗ f^* f∗之间的差异性 ∣ ∣ f ( x k ) − f ∗ ∣ ∣ ||f(x_k) - f^*|| ∣∣f(xk)−f∗∣∣与迭代次数 k k k存在如下函数关系 G ( k ) \mathcal G(k) G(k):
∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ G ( k ) = 1 k ||f(x_k) - f^*|| \leq \mathcal G(k) = \frac{1}{k} ∣∣f(xk)−f∗∣∣≤G(k)=k1
当 k k k充分大时, f ( x k ) , f ( x k + 1 ) f(x_k),f(x_{k+1}) f(xk),f(xk+1)与 f ∗ f^* f∗之间差异性的比值表示如下:
lim k ⇒ ∞ ∣ ∣ f ( x k + 1 ) − f ∗ ∣ ∣ ∣ ∣ f ( x k ) − f ∗ ∣ ∣ = lim k ⇒ ∞ k k + 1 = 1 \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{||f(x_{k+1}) - f^*||}{||f(x_k) - f^*||} = \mathop{\lim}\limits_{k \Rightarrow \infty} \frac{k}{k+1} = 1 k⇒∞lim∣∣f(xk)−f∗∣∣∣∣f(xk+1)−f∗∣∣=k⇒∞limk+1k=1
也就是说:虽然随着 k k k的增加, f ( x k ) f(x_k) f(xk)在减小;但相邻迭代结果 f ( x k ) , f ( x k + 1 ) f(x_k),f(x_{k+1}) f(xk),f(xk+1)之间的差异性几乎可以忽略不计。那么称这种收敛速度为次线性收敛。
准确的说,是 ⇒ 0 \Rightarrow 0 ⇒0的次线性收敛:
lim k ⇒ ∞ { f ( x k ) } ⇒ lim k ⇒ ∞ G ( k ) = 0 \mathop{\lim}\limits_{k \Rightarrow \infty} \{f(x_k)\} \Rightarrow \mathop{\lim}\limits_{k \Rightarrow \infty} \mathcal G(k) = 0 k⇒∞lim{f(xk)}⇒k⇒∞limG(k)=0
二次上界引理
关于二次上界引理的描述表示如下:如果函数 f ( ⋅ ) f(\cdot) f(⋅)可微,并对应梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足利普希兹连续,则函数 f ( ⋅ ) f(\cdot) f(⋅)存在二次上界。即:
∀ x , y ∈ R n ⇒ f ( y ) ≤ f ( x ) + [ ∇ f ( x ) ] T ( y − x ) + L 2 ∣ ∣ y − x ∣ ∣ 2 \forall x,y \in \mathbb R^n \Rightarrow f(y) \leq f(x) + [\nabla f(x)]^T (y - x) + \frac{\mathcal L}{2}||y - x||^2 ∀x,y∈Rn⇒f(y)≤f(x)+[∇f(x)]T(y−x)+2L∣∣y−x∣∣2
而二次上界引理的作用是:可以通过该引理,得到最优步长上界的最小值:
- 假设 x x x固定,令 ϕ ( y ) = f ( x ) + [ ∇ f ( x ) ] T ( y − x ) + L 2 ∣ ∣ y − x ∣ ∣ 2 \begin{aligned}\phi(y) = f(x) + [\nabla f(x)]^T (y - x) + \frac{\mathcal L}{2}||y - x||^2 \end{aligned} ϕ(y)=f(x)+[∇f(x)]T(y−x)+2L∣∣y−x∣∣2,通过选择合适的 y m i n y_{min} ymin,使 ϕ ( y ) \phi(y) ϕ(y)达到最小值:
y m i n = arg min y ∈ R n ϕ ( y ) y_{min} = \mathop{\arg\min}\limits_{y \in \mathbb R^n} \phi(y) ymin=y∈Rnargminϕ(y) - 令 ∇ ϕ ( y ) ≜ 0 \nabla \phi(y) \triangleq 0 ∇ϕ(y)≜0,有:
y m i n = x + 1 L ⋅ [ − ∇ f ( x ) ] y_{min} = x + \frac{1}{\mathcal L} \cdot [- \nabla f(x)] ymin=x+L1⋅[−∇f(x)] - 其中 − ∇ f ( x ) - \nabla f(x) −∇f(x)即 P k \mathcal P_k Pk,也就是最速下降方向;而 1 L \begin{aligned}\frac{1}{\mathcal L}\end{aligned} L1则是最优步长的上确界:
f ( y ) ≤ ϕ ( y m i n ) = min y ∈ R n ϕ ( y ) f(y) \leq \phi(y_{min}) = \mathop{\min}\limits_{y \in \mathbb R^n} \phi(y) f(y)≤ϕ(ymin)=y∈Rnminϕ(y)
也就是说:- 在没有二次上界引理的约束下,步长 α k \alpha_k αk的选择在其定义域内没有约束: ( 0 , + ∞ ) (0, +\infty) (0,+∞);
- 经过二次上界引理的约束后,步长 α k \alpha_k αk的选择从原始的 ( 0 , + ∞ ) (0,+\infty) (0,+∞)约束至 ( 0 , 1 L ] \begin{aligned}\left(0,\frac{1}{\mathcal L}\right]\end{aligned} (0,L1]。
延伸:关于区间 ( 0 , 1 L ] \begin{aligned}\left(0,\frac{1}{\mathcal L}\right]\end{aligned} (0,L1]可以模糊地认为满足 Armijo \text{Armijo} Armijo准则。关于步长变量 α \alpha α的函数 ϕ ( α ) = f ( x k + 1 ) \phi(\alpha) = f(x_{k+1}) ϕ(α)=f(xk+1)中,当 α ∈ ( 0 , 1 L ] \alpha \in \begin{aligned}\left(0,\frac{1}{\mathcal L}\right]\end{aligned} α∈(0,L1]时,等价于:存在一条直线 L ( α ) \mathcal L(\alpha) L(α),以该直线作为划分边界对应 α \alpha α的范围正好是 ( 0 , 1 L ] \begin{aligned}\left(0,\frac{1}{\mathcal L}\right]\end{aligned} (0,L1]:
吐槽:实际上用这张图是不太合理的,因为下面的图对应的 f ( ⋅ ) f(\cdot) f(⋅)更加复杂,二次上界约束的范围仅仅在下面 α \alpha α轴的绿色实线部分,但很明显,在该函数中,存在更优质的 α \alpha α结果。

梯度下降法在凸函数上的收敛性
收敛性定理介绍
梯度下降法在凸函数上的收敛性定理表示如下:
- 条件:
- 函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,在定义域内可微,并且 f ( ⋅ ) f(\cdot) f(⋅)是凸函数;
- 关于 f ( ⋅ ) f(\cdot) f(⋅)的梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足利普希兹连续;
- 梯度下降法迭代过程中步长 α k ( k = 1 , 2 , 3 , ⋯ ) \alpha_k(k=1,2,3,\cdots) αk(k=1,2,3,⋯)有明确的约束范围: α k ∈ ( 0 , 1 L ] \begin{aligned}\alpha_k \in \left(0,\frac{1}{\mathcal L} \right]\end{aligned} αk∈(0,L1];
- 结论:数值解序列 { x k } k = 0 ∞ \{x_{k}\}_{k=0}^{\infty} {xk}k=0∞对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞以 O ( 1 k ) \begin{aligned}\mathcal O \left(\frac{1}{k}\right)\end{aligned} O(k1)收敛于目标函数最优解 f ∗ f^* f∗。
其中O ( 1 k ) \begin{aligned}\mathcal O \left(\frac{1}{k}\right)\end{aligned} O(k1)表示以G ( k ) = C ⋅ 1 k \begin{aligned}\mathcal G(k) = \mathcal C \cdot \frac{1}{k}\end{aligned} G(k)=C⋅k1的次线性收敛级别的收敛速度(C \mathcal C C为常数)。
证明过程
根据二次上界引理,依然将 x x x设为上一次迭代的数值解 x i − 1 x_{i-1} xi−1,对应的 y y y为当前迭代步骤的数值解 x i x_i xi。由于是梯度下降法,因而在线搜索方法的基础上,将方向 P i \mathcal P_i Pi表示为最速下降方向 ∇ f ( x i − 1 ) \nabla f(x_{i-1}) ∇f(xi−1)步长依然使用步长变量 α \alpha α进行表示:
y − x = x i − x i − 1 = − ∇ f ( x i − 1 ) ⋅ α y - x = x_i - x_{i - 1} = -\nabla f(x_{i-1}) \cdot \alpha y−x=xi−xi−1=−∇f(xi−1)⋅α
将二次上界不等式进行相应替换:
将上式代入~
f ( x i ) ≤ f ( x i − 1 ) + [ ∇ f ( x i − 1 ) ] T [ − ∇ f ( x i − 1 ) ⋅ α ] + L 2 ∣ ∣ − ∇ f ( x i − 1 ) ⋅ α ∣ ∣ 2 f(x_i) \leq f(x_{i-1}) + [\nabla f(x_{i-1})]^T [-\nabla f(x_{i-1}) \cdot \alpha] + \frac{\mathcal L}{2} ||-\nabla f(x_{i-1}) \cdot \alpha||^2 f(xi)≤f(xi−1)+[∇f(xi−1)]T[−∇f(xi−1)⋅α]+2L∣∣−∇f(xi−1)⋅α∣∣2
观察不等式右侧,可以继续化简:
将内积写作∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||^2 ∣∣⋅∣∣2的形式。- ∣ ∣ − ∇ f ( x i − 1 ) ⋅ α ∣ ∣ 2 = ∣ ∣ ∇ f ( x i − 1 ) ⋅ α ∣ ∣ 2 ||- \nabla f(x_{i-1}) \cdot \alpha||^2 = ||\nabla f(x_{i-1}) \cdot \alpha||^2 ∣∣−∇f(xi−1)⋅α∣∣2=∣∣∇f(xi−1)⋅α∣∣2
,这里消掉一个负号; 由于α ∈ ( 0 , 1 L ] \begin{aligned}\alpha \in \left(0,\frac{1}{\mathcal L}\right]\end{aligned} α∈(0,L1],是一个标量,直接将其提到范数外侧。
I r i g h t = f ( x i − 1 ) − α ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 + L 2 ⋅ α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 \mathcal I_{right} = f(x_{i-1}) - \alpha \cdot ||\nabla f(x_{i-1})||^2 + \frac{\mathcal L}{2} \cdot \alpha^2 \cdot ||\nabla f(x_{i-1})||^2 Iright=f(xi−1)−α⋅∣∣∇f(xi−1)∣∣2+2L⋅α2⋅∣∣∇f(xi−1)∣∣2
由 α ≤ 1 L \begin{aligned}\alpha \leq \frac{1}{\mathcal L}\end{aligned} α≤L1可知: L ≤ 1 α \begin{aligned}\mathcal L \leq \frac{1}{\alpha} \end{aligned} L≤α1。将该式代入到上式中:
消掉分母中的 α \alpha α,并于前面的项结合。
I r i g h t ≤ f ( x i − 1 ) − α ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 + 1 2 α ⋅ α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 = f ( x i − 1 ) − α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 \begin{aligned} \mathcal I_{right} & \leq f(x_{i-1}) - \alpha \cdot ||\nabla f(x_{i-1})||^2 + \frac{1}{2 \alpha} \cdot \alpha^2 \cdot ||\nabla f(x_{i-1})||^2 \\ & = f(x_{i-1}) - \frac{\alpha}{2} \cdot ||\nabla f(x_{i-1})||^2 \end{aligned} Iright≤f(xi−1)−α⋅∣∣∇f(xi−1)∣∣2+2α1⋅α2⋅∣∣∇f(xi−1)∣∣2=f(xi−1)−2α⋅∣∣∇f(xi−1)∣∣2
基于梯度下降法,使用二次上界引理,可以得到 f ( x i − 1 ) f(x_{i-1}) f(xi−1)与 f ( x i ) f(x_i) f(xi)之间存在如下关联关系:
f ( x i ) ≤ f ( x i − 1 ) − α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 i = 1 , 2 , 3 , ⋯ f(x_i) \leq f(x_{i-1}) - \frac{\alpha}{2} \cdot ||\nabla f(x_{i-1})||^2\quad i=1,2,3,\cdots f(xi)≤f(xi−1)−2α⋅∣∣∇f(xi−1)∣∣2i=1,2,3,⋯
根据凸函数的性质,必然有:函数 f ( ⋅ ) f(\cdot) f(⋅)任一位置的切线, f ( ⋅ ) f(\cdot) f(⋅)均在该切线上方。见下图:
由于条件: f ( ⋅ ) f(\cdot) f(⋅)向下有界,因此,该函数必然’开口向上‘。
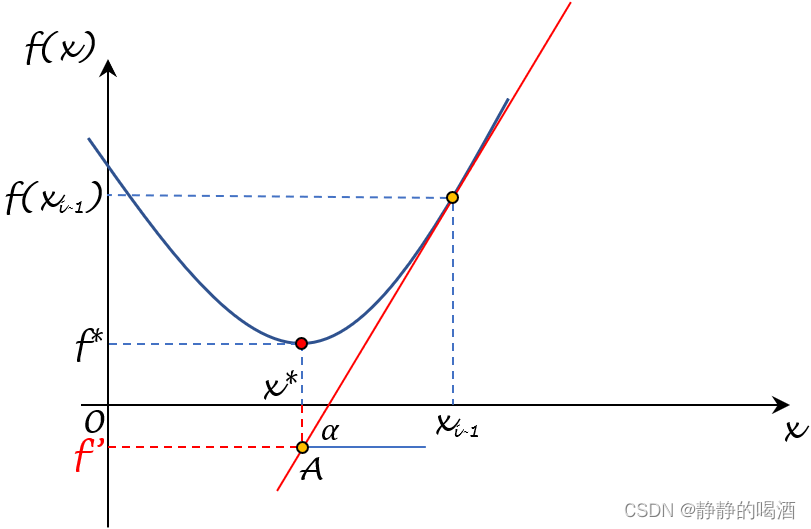
其中红色点 ( x ∗ , f ∗ ) (x^*,f^*) (x∗,f∗)表示最优点,以上一次迭代产生的 x i − 1 x_{i-1} xi−1为切点做一条切线,必然有 x ∗ x^* x∗在该切线函数上的函数值 f ′ ≤ f ∗ f' \leq f^* f′≤f∗。 f ′ f' f′表示如下:
f ′ = f ( x i − 1 ) − [ ∇ f ( x i − 1 ) ] T ( x i − 1 − x ∗ ) ≤ f ∗ f' = f(x_{i-1}) - [\nabla f(x_{i-1})]^T (x_{i-1} - x^*) \leq f^* f′=f(xi−1)−[∇f(xi−1)]T(xi−1−x∗)≤f∗
移项,从而有:
f ( x i − 1 ) ≤ f ∗ + [ ∇ f ( x i − 1 ) ] T ( x i − 1 − x ∗ ) f(x_{i-1}) \leq f^* + [\nabla f(x_{i-1})]^T (x_{i-1} - x^*) f(xi−1)≤f∗+[∇f(xi−1)]T(xi−1−x∗)
将上式代入,有:
I r i g h t ≤ f ∗ + [ ∇ f ( x i − 1 ) ] T ( x i − 1 − x ∗ ) ⏟ 替换 f ( x i − 1 ) − α 2 ⋅ ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 \mathcal I_{right} \leq \underbrace{f^* + [\nabla f(x_{i-1})]^T (x_{i-1} - x^*)}_{替换f(x_{i-1})}- \frac{\alpha}{2} \cdot ||\nabla f(x_{i-1})||^2 Iright≤替换f(xi−1) f∗+[∇f(xi−1)]T(xi−1−x∗)−2α⋅∣∣∇f(xi−1)∣∣2
为了凑平方项,将上式调整至如下形式:
将 − α 2 \begin{aligned}-\frac{\alpha}{2}\end{aligned} −2α凑出 α 2 \alpha^2 α2,其他项跟随变化。
I r i g h t ≤ − 1 2 α { α 2 ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 − 2 α ⋅ [ ∇ f ( x i − 1 ) ] T ( x i − 1 − x ∗ ) } \mathcal I_{right} \leq -\frac{1}{2 \alpha} \left\{\alpha^2 ||\nabla f(x_{i-1})||^2 - 2\alpha \cdot [\nabla f(x_{i-1})]^T(x_{i-1} - x^*)\right\} Iright≤−2α1{α2∣∣∇f(xi−1)∣∣2−2α⋅[∇f(xi−1)]T(xi−1−x∗)}
对大括号内的项进行配方:
I r i g h t ≤ f ∗ − 1 2 α { α 2 ∣ ∣ ∇ f ( x i − 1 ) ∣ ∣ 2 − 2 α ⋅ [ ∇ f ( x i − 1 ) ] T ( x i − 1 − x ∗ ) + ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 ⏟ 平方项 − ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 } = f ∗ − 1 2 α [ ∣ ∣ α ⋅ ∇ f ( x i − 1 ) − ( x i − 1 − x ∗ ) ∣ ∣ 2 − ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 ] \begin{aligned} \mathcal I_{right} & \leq f^* - \frac{1}{2 \alpha} \left\{\underbrace{\alpha^2 ||\nabla f(x_{i-1})||^2 - 2\alpha \cdot [\nabla f(x_{i-1})]^T(x_{i-1} - x^*) + ||x_{i-1} - x^*||^2 }_{平方项}- ||x_{i-1} - x^*||^2\right\} \\ & = f^* - \frac{1}{2\alpha} \left [||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2 - ||x_{i-1} - x^*||^2\right] \end{aligned} Iright≤f∗−2α1⎩ ⎨ ⎧平方项 α2∣∣∇f(xi−1)∣∣2−2α⋅[∇f(xi−1)]T(xi−1−x∗)+∣∣xi−1−x∗∣∣2−∣∣xi−1−x∗∣∣2⎭ ⎬ ⎫=f∗−2α1[∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2−∣∣xi−1−x∗∣∣2]
观察中括号内第一项: ∣ ∣ α ⋅ ∇ f ( x i − 1 ) − ( x i − 1 − x ∗ ) ∣ ∣ 2 ||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2 ∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2,由于是范数的平方项,因而在范数内部添加一个负号不会影响其值的变化:
∣ ∣ α ⋅ ∇ f ( x i − 1 ) − ( x i − 1 − x ∗ ) ∣ ∣ 2 = ∣ ∣ x i − 1 − α ⋅ ∇ f ( x i − 1 ) − x ∗ ∣ ∣ 2 ||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2 = ||x_{i-1} - \alpha \cdot \nabla f(x_{i-1}) - x^*||^2 ∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2=∣∣xi−1−α⋅∇f(xi−1)−x∗∣∣2
从迭代角度观察: x i − 1 − α ⋅ ∇ f ( x i − 1 ) = x i x_{i-1} - \alpha \cdot \nabla f(x_{i-1}) = x_{i} xi−1−α⋅∇f(xi−1)=xi,从而上式可继续化简为:
提一个负号,调换一下位置。
{ ∣ ∣ α ⋅ ∇ f ( x i − 1 ) − ( x i − 1 − x ∗ ) ∣ ∣ 2 = ∣ ∣ x i − x ∗ ∣ ∣ 2 I r i g h t ≤ f ∗ − 1 2 α [ ∣ ∣ x i − x ∗ ∣ ∣ 2 − ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 ] = f ∗ + 1 2 α [ ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 − ∣ ∣ x i − x ∗ ∣ ∣ 2 ] \begin{cases} ||\alpha \cdot \nabla f(x_{i-1}) - (x_{i-1} - x^*)||^2 = ||x_i - x^*||^2 \\ \quad \\ \begin{aligned} \mathcal I_{right} & \leq f^* - \frac{1}{2\alpha} \left[||x_i - x^*||^2 - ||x_{i-1} - x^*||^2\right] \\ & = f^* + \frac{1}{2\alpha} \left[||x_{i-1} - x^*||^2 - ||x_i - x^*||^2\right] \end{aligned} \end{cases} ⎩ ⎨ ⎧∣∣α⋅∇f(xi−1)−(xi−1−x∗)∣∣2=∣∣xi−x∗∣∣2Iright≤f∗−2α1[∣∣xi−x∗∣∣2−∣∣xi−1−x∗∣∣2]=f∗+2α1[∣∣xi−1−x∗∣∣2−∣∣xi−x∗∣∣2]
至此,可以得到如下不等式结果:
f ( x i ) − f ∗ ≤ 1 2 α ( ∣ ∣ x i − 1 − x ∗ ∣ ∣ 2 − ∣ ∣ x i − x ∗ ∣ ∣ 2 ) f(x_i) - f^* \leq \frac{1}{2\alpha}(||x_{i-1} - x^*||^2 - ||x_i - x^*||^2) f(xi)−f∗≤2α1(∣∣xi−1−x∗∣∣2−∣∣xi−x∗∣∣2)
观察:不等式左侧描述的意义是:当前迭代步骤的目标函数结果 f ( x i ) f(x_i) f(xi)与最优解 f ∗ f^* f∗之间的偏差。从初始化数值解 x 0 x_0 x0开始,我们会得到一系列的不等式结果:
{ f ( x 1 ) − f ∗ ≤ 1 2 α ( ∣ ∣ x 0 − x ∗ ∣ ∣ 2 − ∣ ∣ x 1 − x ∗ ∣ ∣ 2 ) f ( x 2 ) − f ∗ ≤ 1 2 α ( ∣ ∣ x 1 − x ∗ ∣ ∣ 2 − ∣ ∣ x 2 − x ∗ ∣ ∣ 2 ) ⋮ f ( x k ) − f ∗ ≤ 1 2 α ( ∣ ∣ x k − 1 − x ∗ ∣ ∣ 2 − ∣ ∣ x k − x ∗ ∣ ∣ 2 ) \begin{cases} \begin{aligned} f(x_1) - f^* & \leq \frac{1}{2\alpha} (||x_0 - x^*||^2 - ||x_1 - x^*||^2) \\ f(x_2) - f^* & \leq \frac{1}{2\alpha} (||x_1 - x^*||^2 - ||x_2 - x^*||^2) \\ & \vdots \\ f(x_k) - f^* & \leq \frac{1}{2\alpha} (||x_{k-1} - x^*||^2 - ||x_k - x^*||^2) \end{aligned} \end{cases} ⎩ ⎨ ⎧f(x1)−f∗f(x2)−f∗f(xk)−f∗≤2α1(∣∣x0−x∗∣∣2−∣∣x1−x∗∣∣2)≤2α1(∣∣x1−x∗∣∣2−∣∣x2−x∗∣∣2)⋮≤2α1(∣∣xk−1−x∗∣∣2−∣∣xk−x∗∣∣2)
将这些不等式对应位置相加,有:
等式右侧的中间项都被消掉了~因为∣ ∣ x k − x ∗ ∣ ∣ 2 ≥ 0 ||x_k - x^*||^2 \geq 0 ∣∣xk−x∗∣∣2≥0恒成立,从而消掉含变量的项。
∑ i = 1 k [ f ( x i ) − f ∗ ] ≤ 1 2 α ( ∣ ∣ ∣ x 0 − x ∗ ∣ ∣ 2 − ∣ ∣ x k − x ∗ ∣ ∣ 2 ) ≤ 1 2 α ∣ ∣ x 0 − x ∗ ∣ ∣ 2 \sum_{i=1}^k [f(x_i) - f^*] \leq \frac{1}{2\alpha}(|||x_0 - x^*||^2 - ||x_k - x^*||^2) \leq \frac{1}{2 \alpha} ||x_0 - x^*||^2 i=1∑k[f(xi)−f∗]≤2α1(∣∣∣x0−x∗∣∣2−∣∣xk−x∗∣∣2)≤2α1∣∣x0−x∗∣∣2
关于我们要证的 ∣ ∣ f ( x k ) − f ∗ ∣ ∣ ||f(x_k) - f^*|| ∣∣f(xk)−f∗∣∣,可以表示为如下形式:
由于优化问题的收敛性,必然有: f ( x k ) ≤ f ( x k − 1 ) ≤ ⋯ ≤ f ( x 1 ) f(x_{k}) \leq f(x_{k-1})\leq \cdots\leq f(x_1) f(xk)≤f(xk−1)≤⋯≤f(x1),从而每一项:∣ ∣ f ( x k ) − f ∗ ∣ ∣ ≤ ∣ ∣ f ( x k − 1 ) − f ∗ ∣ ∣ ≤ ⋯ ≤ ∣ ∣ f ( x 1 ) − f ∗ ∣ ∣ ||f(x_k) - f^*|| \leq ||f(x_{k-1}) - f^*|| \leq \cdots \leq ||f(x_1) - f^*|| ∣∣f(xk)−f∗∣∣≤∣∣f(xk−1)−f∗∣∣≤⋯≤∣∣f(x1)−f∗∣∣,从而有:∑ i = 1 k [ f ( x k ) − f ∗ ] ≤ ∑ i = 1 k [ f ( x i ) − f ∗ ] \begin{aligned}\sum_{i=1}^k[f(x_k) - f^*] \leq \sum_{i=1}^{k} [f(x_i) - f^*]\end{aligned} i=1∑k[f(xk)−f∗]≤i=1∑k[f(xi)−f∗]。将上式结果带入~
f ( x k ) − f ∗ = 1 k ∑ i = 1 k [ f ( x k ) − f ∗ ] ≤ 1 k ∑ i = 1 k [ f ( x i ) − f ∗ ] ≤ 1 k [ 1 2 α ∣ ∣ x 0 − x ∗ ∣ ∣ 2 ] f(x_k) - f^* = \frac{1}{k} \sum_{i=1}^{k}[f(x_k) - f^*] \leq \frac{1}{k} \sum_{i=1}^{k}[f(x_i) - f^*] \leq \frac{1}{k} \left[\frac{1}{2\alpha}||x_0 - x^*||^2\right] f(xk)−f∗=k1i=1∑k[f(xk)−f∗]≤k1i=1∑k[f(xi)−f∗]≤k1[2α1∣∣x0−x∗∣∣2]
观察: [ 1 2 α ∣ ∣ x 0 − x ∗ ∣ ∣ 2 ] \begin{aligned}\left[\frac{1}{2\alpha}||x_0 - x^*||^2\right]\end{aligned} [2α1∣∣x0−x∗∣∣2]中 α ∈ ( 0 , 1 L ] \begin{aligned}\alpha \in \left(0,\frac{1}{\mathcal L} \right] \end{aligned} α∈(0,L1], x 0 , x ∗ x_0,x^* x0,x∗都是确定的常数,因而该项可视作常数 C \mathcal C C。最终有:
f ( x k ) − f ∗ ≤ 1 k ⋅ C f(x_k) - f^* \leq \frac{1}{k} \cdot \mathcal C f(xk)−f∗≤k1⋅C
我们可以令 G ( k ) = 1 k ⋅ C \begin{aligned}\mathcal G(k) = \frac{1}{k} \cdot \mathcal C\end{aligned} G(k)=k1⋅C,可以看出:它就是一个级别为 1 k \begin{aligned}\frac{1}{k}\end{aligned} k1的次线性收敛。
相关参考:
【优化算法】梯度下降法-凸函数的收敛性
相关文章:

机器学习笔记值优化算法(十四)梯度下降法在凸函数上的收敛性
机器学习笔记之优化算法——梯度下降法在凸函数上的收敛性 引言回顾:收敛速度:次线性收敛二次上界引理 梯度下降法在凸函数上的收敛性收敛性定理介绍证明过程 引言 本节将介绍梯度下降法在凸函数上的收敛性。 回顾: 收敛速度:次…...
iphone拷贝照片中间带E自动去重软件,以及java程序如何打包成jar和exe
文章目录 一、前提二、问题描述三、原始处理方式四、程序处理4.1 java程序如何打包exe4.1.1 首先打包jar4.1.2 开始生成exe4.1.3 软件使用方式 4.2 更换图标4.2.1 更换swing的打包jar图标4.2.2 更换exe图标 4.3 如何使生成的exe在没有java环境的电脑上运行4.3.1 Inno Setup打包…...

不同分类器对数据的处理
"""基于鸢尾花的不同分类器的效果比对:step1:准备数据;提取数据的特征向量X,Y将Y数据采用LabelEncoder转化为数值型数据;step2:将提取的特征向量X,Y进行拆分(训练集与测试集)step3:构建不同分类器并设置参数,例如:…...

十面骰子、
十面骰子(一): v 有一个十面的骰子,每一面分别为1-10,不断投掷骰子,投10000次,统计每一面1-10出现的次数或概率. v 提示:可用rand()产生1-10之间的随机数,再统计1-10出现的机会,存放于数组里,…...
IDE的下载和使用
IDE 文章目录 IDEJETBRAIN JETBRAIN 官网下载对应的ide 激活方式 dxm的电脑已经把这个脚本下载下来了,脚本是macjihuo 以后就不用买了...

华为OD机试真题【字母组合】
1、题目描述 【字母组合】 数字0、1、2、3、4、5、6、7、8、9分别关联 a~z 26个英文字母。 0 关联 “a”,”b”,”c” 1 关联 “d”,”e”,”f” 2 关联 “g”,”h”,”i” 3 关联 “j”,”k”,”l” 4 关联 “m”,”n”,”o” 5 关联 “p”,”q”,”r” 6 关联 “s”,”t” 7…...
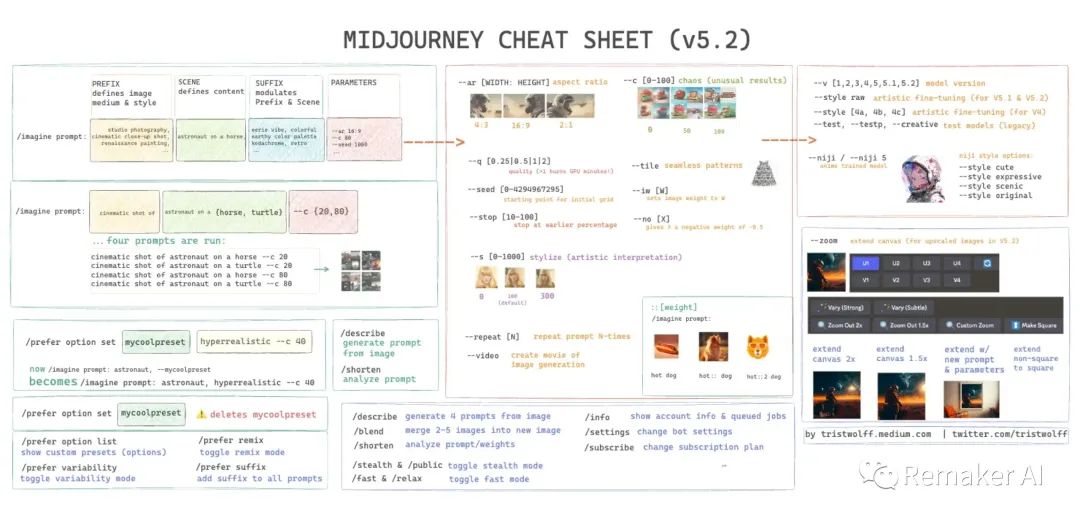
Midjourney Prompt 提示词速查表 v5.2
Midjourney 最新的版本更新正不断推出令人兴奋的新功能。这虽然不断扩展了我们的AI绘图工具箱,但有时也会让我们难以掌握所有实际可以使用的功能和参数。 针对此问题, 小编整理了 "Midjourney Prompt 提示词速查表",这是一个非常方便的 Midjo…...

自动驾驶——驶向未来的革命性技术
自动驾驶——驶向未来的革命性技术 自动驾驶的组件自动驾驶的优势自动驾驶的应用自动驾驶的未来中国的自动驾驶 自动驾驶是一种技术,它允许车辆在没有人类驾驶员的情况下自主地进行行驶。它利用各种传感器、计算机视觉、人工智能和机器学习算法来感知和理解周围环境…...
 甲级 1004 Counting Leaves)
PAT (Advanced Level) 甲级 1004 Counting Leaves
点此查看所有题目集 A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child. Input Specification: Each input file contains one test case. Each case starts with a line containing 0<N<100, …...
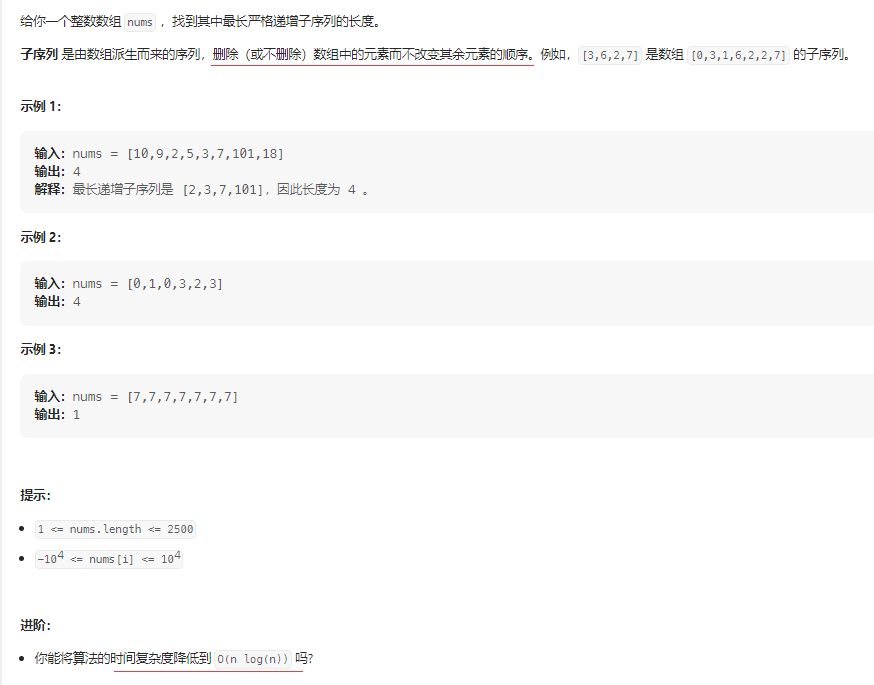
最长递增子序列——力扣300
int lengthOfLIS(vector<int>& nums) {int len=1, n=nums.size();if...

邮递员送信 单源最短路+反向建边
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n−1 n−1样东西,其目的地分别是节点 2 2 2到节点 n n n。所有的道路都是单行的,共有 m m m条道路。邮递员每次只能带一样东西,运送每件物品过后必须返回邮局。求送完东…...

git的常用操作
1. git查看dev分支与master分支的情况 要查看特定分支(如dev和master)的情况,您可以使用以下命令: git log --oneline master..dev 这将显示在dev分支上存在但不在master分支上的提交记录的简要信息。每条记录都包括提交的哈希…...
vscode搭建java开发环境
一、配置extensions环境变量VSCODE_EXTENSIONS, 该环境变量路径下的存放安装组件: 二、setting配置文件 {"java.jdt.ls.java.home": "e:\\software\\jdk\\jdk17",// java运行环境"java.configuration.runtimes": [{"…...

01 qt快速入门
一 qt介绍 1.基本概念 1991年由Qt Company(奇趣)开发的跨平台C++图形用户界面应用程序开发框架,GUI程序和非GUI程序。优点:一套源码在不同的平台通过不同的编译器进行编译,就可以运行到该平台上目标机。面向对象的封装机制来对其接口封装。 GUI —图形用户界面(Graphic…...

嵌入式开发中常用且杂散的命令
1、mount命令 # 挂载linux系统 mkdir /tmp/share mount -t nfs 10.77.66.88:/share/ /tmp/share -o nolock,tcp cd /tmp/share# 挂载Windows系统 mkdir /tmp/windows mount -t nfs 10.66.77.88:/c/public /tmp/windows -o nolock,tcp cd /tmp/windows# 挂载vfat格式的U盘 mkdi…...

JS导出复杂多级表头的Excel
使用方式 1、安装依赖 npm install xlsx-js-style2、复制代码文件exportExcel.js至工程 https://github.com/EnthuDai/export-excel-in-one-line 3、在引入excel.js后调用 Excel.export(columns, dataSource, 导出文件名)4、代码demo 5、效果 页面excel 适用范围 对于使…...

2023国赛数学建模E题思路分析
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...

【JavaScript 12】二进制位运算符 或 与 非 异或 左移 右移 头部补零右移
二进制位运算符 概述 概述 7个用于直接对二进制位进行运算 二进制或 or | 若两个二进制位都为0则为0,否则为1二进制与 and & 若两个二进制位都为1则为1,否则为0二进制非 not ~ 对一个二进制位取反异或 xor ^ 若两个二进制位不同则为1,否…...

Kafka 入门到起飞 - Kafka是怎么保证可靠性的呢
在这里插入图片描述 我们已经了解到,复习一下 创建topic时,可以指定副本因子 repilication-factor 3 表示分区的副本数,包括Leader分区副本和follower分区副本不要超过broker的数量,尽量保证一个分区的副本均匀分散不同的broker…...

数学建模(三)整数规划
视频推荐:B站_数学建模老哥 一、整数规划基本原理 数学规划中的变量(部分或全部)限制为整数时,称为整数规划。若在线性规划模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法&am…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
