C++ 动态规划经典案例解析之最长公共子序列(LCS)_窥探递归和动态规划的一致性
1. 前言
动态规划处理字符相关案例中,求最长公共子序列以及求最短编辑距离,算是经典中的经典案例。
讲解此类问题的算法在网上一抓应用一大把,即便如此,还是忍不住有写此文的想法。毕竟理解、看懂都不算是真正掌握,唯有瞧出其中玄机,能有自己独有的见解和不一样的感悟方算是把知识学到灵魂深入。
好了!闲话少说,进入正题。
2. 最长公共子序列(LCS)
2.1 问题描述
最长公共子序列,指找出 2 个或多个字符串中的最长公共子序列。
如字符串 s1=kabc和s2=taijc,其最长公共子序列是ac。
Tips: 子序列只要求其中字符保持和原字符串中一样的顺序,而不一定连续。
2.2 递归思想
这是一道求最值的题目,只要是求最值,必然会存在多个选择,原理很简单,如果没有多个选择,还有必要纠结谁是最大谁是最小吗?
Tips: 在你面前有苹果、桔子、香蕉……你只能选择一个,这时候方有纠结。如果面前只有苹果,还会纠结吗?
面对此问题,可以采用化整为零的思想,从宏观层面转移到微观层面,缩小问题的规模的递归思想。
如为字符串s1设置位置指针 i,为字符串s2设置位置指针j,则问题可以抽象为如下函数。函数的语义:i和j作为起始位置时字符串s1,s2的最长公共子序列。
int lcs(string s1,int i,string s2,int j);
//如果 s1、s2为全局变量,函数可以是
int lcs(int i,int j);
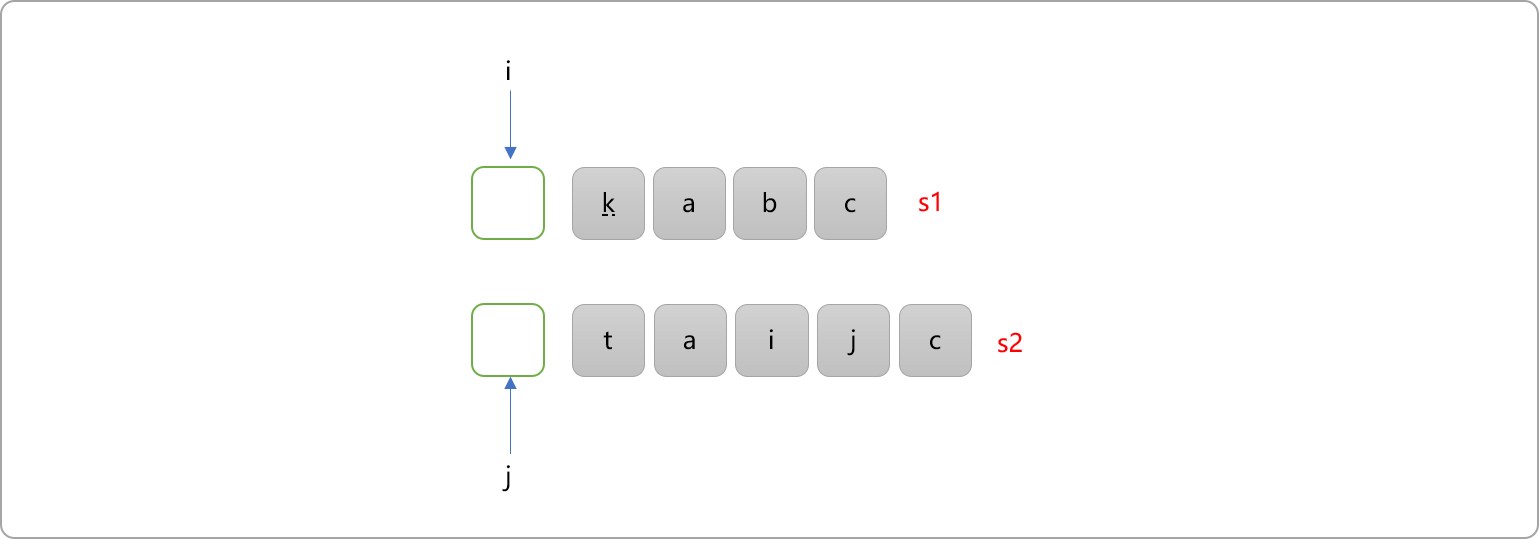
- 初始时,
i=0和j=0意味求解完整的s1和s2的最长公共子序列。此时规模最大,无法直接得到答案。如此,把问题延续到规模较小的子问题。
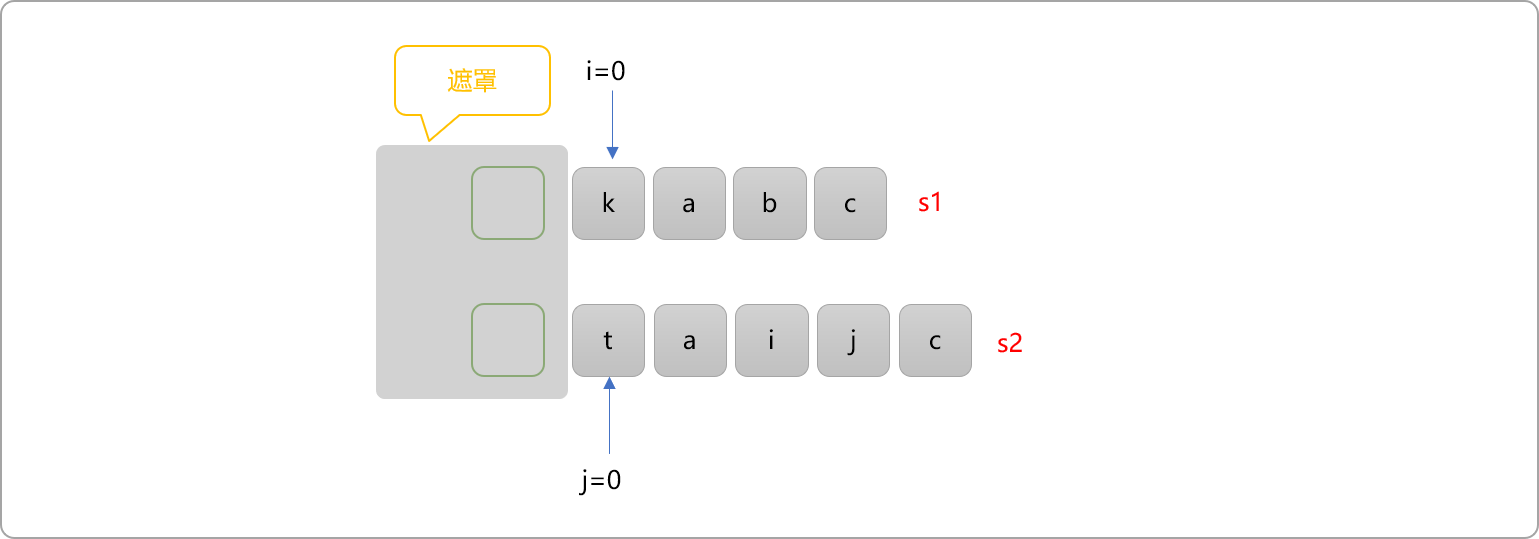
上文说过,求最值一定存在多个选择的,原始问题中的k!=t,则可存在如下 3 种选择:
A、i不动,j+1。即把i指向作为起始位置的s1字符串和j+1作为起始位置的s2字符串继续比较。可算为一个子问题。
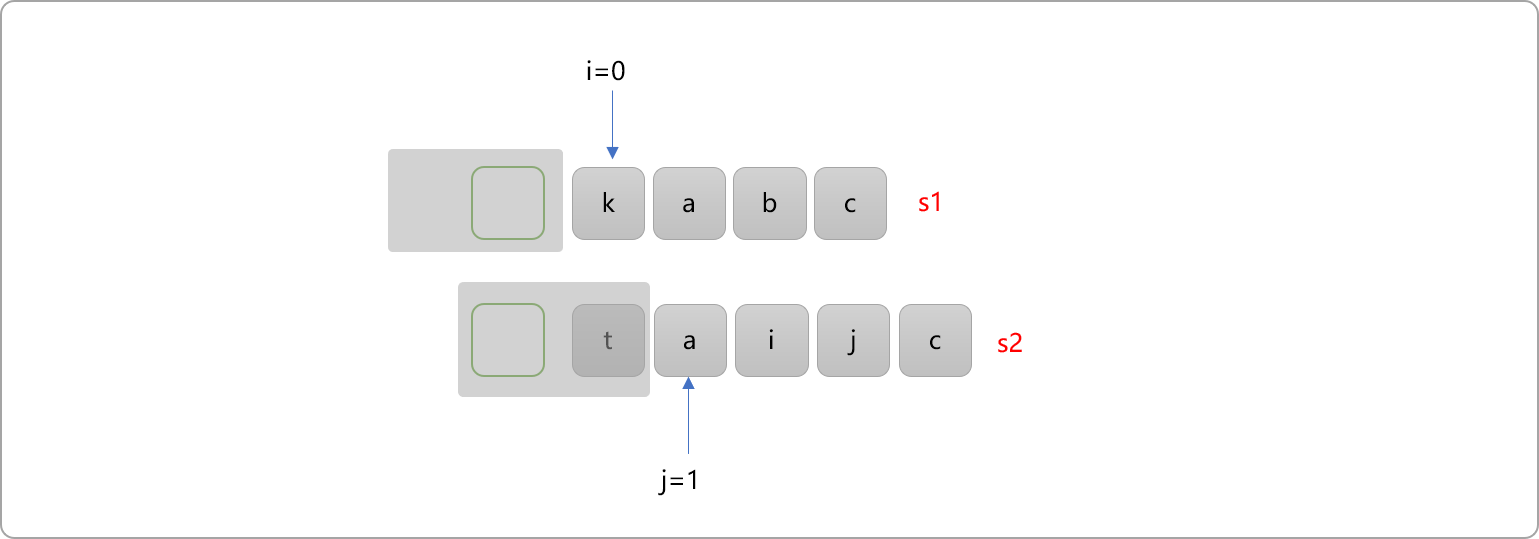
B、j不动,i+1。即把i+1指向作为起始位置的s1字符串和j作为起始位置的s2字符串继续比较。可算为另一个子问题。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cr2f8B0w-1691975983175)(D:\红泥巴\我的课程体系\数据结构与算法\动态规划系列\images\44.png)]
C、i和j同时移动到下一个位置。即把i+1指向作为起始位置的s1字符串和j+1作为起始位置的s2字符串继续比较。也算为一个子问题。

也就是说,当原始问题中i和j指向位置字符不相同时,存在 3 个选择。至于子问题如何求解,这个归功于递归思想。
Tips: 递归最大的好处就是只需要确定基础函数的功能,然后确定子问题,则子问题的内部如何求解站在宏观角度可以不管。反之它可以一步一步继续缩小问题规模,直到有答案为止。
然后在3 种选择中,返回值最大的那一个作为当前的问题的结果。
int lcs(string s1,int i,string s2,int j){if(s1[i]!=s2[j]){//有 3 种选择int sel_1=lcs(s1,i,s2,j+1);int sel_2=lcs(s1,i+1,s2,j);int sel_3=lcs(s1,i+1,s2,j+1);return max(sel_1,sel_2,sel_3);}
}
-
如下图所示,当
i和j所指向位置的值相同时,必然在当前子问题中就找到了一个公共字符,则最终结果就是后续子问题的结果基础上加 1 ,则为最长公共子序列为原来的值加1。Tips: 在海滩上捡贝壳时,当前拾到了一个,回家时最终能拾到的贝壳一定是当前拾到的这一个加上后续所拾到的贝壳。
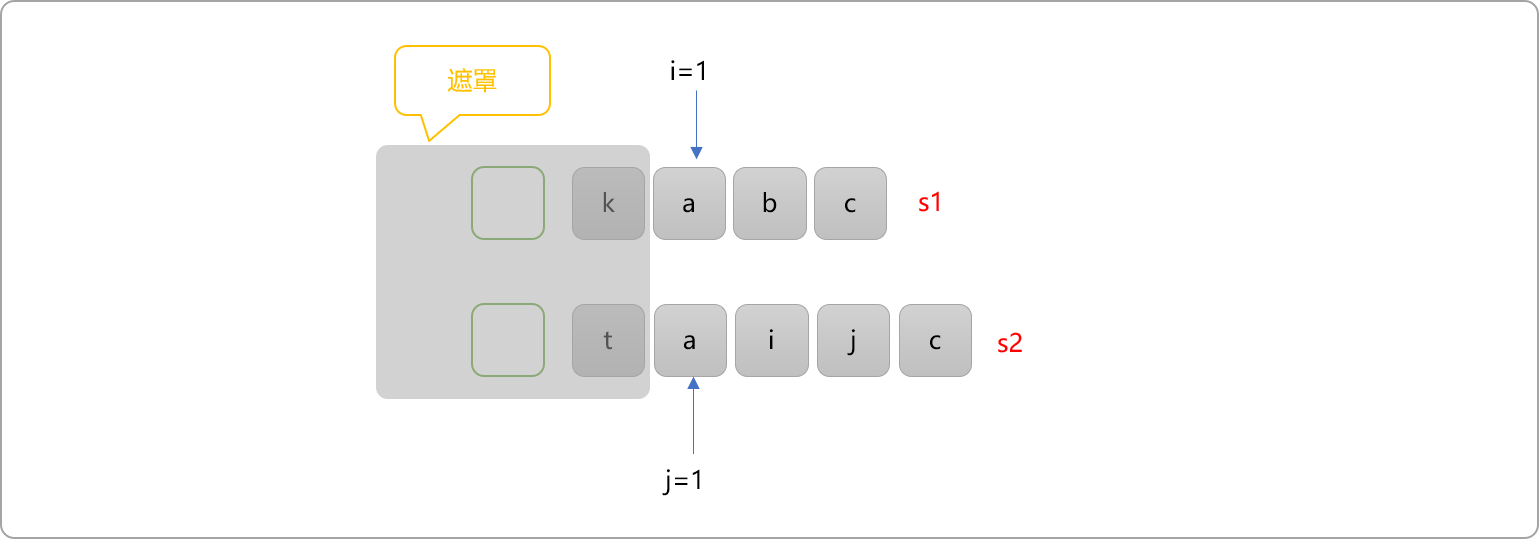
同时移动 i和j,进入规模较小的子问题。如下图所示。
此时可总结一下,使用递归求最长公共子序列,类似于玩消消乐,相同,则消掉,直接进入剩下的内容。不相同,选择会多些。

int lcs(string s1,int i,string s2,int j){if(s1[i]!=s2[j]){//有 3 种选择int sel_1=lcs(s1,i,s2,j+1);int sel_2=lcs(s1,i+1,s2,j);int sel_3=lcs(s1,i+1,s2,j+1);//三者之中选择最大返回值}else{//只有一个选择return lcs(s1,i+1,s2,j+1)+1;}
}
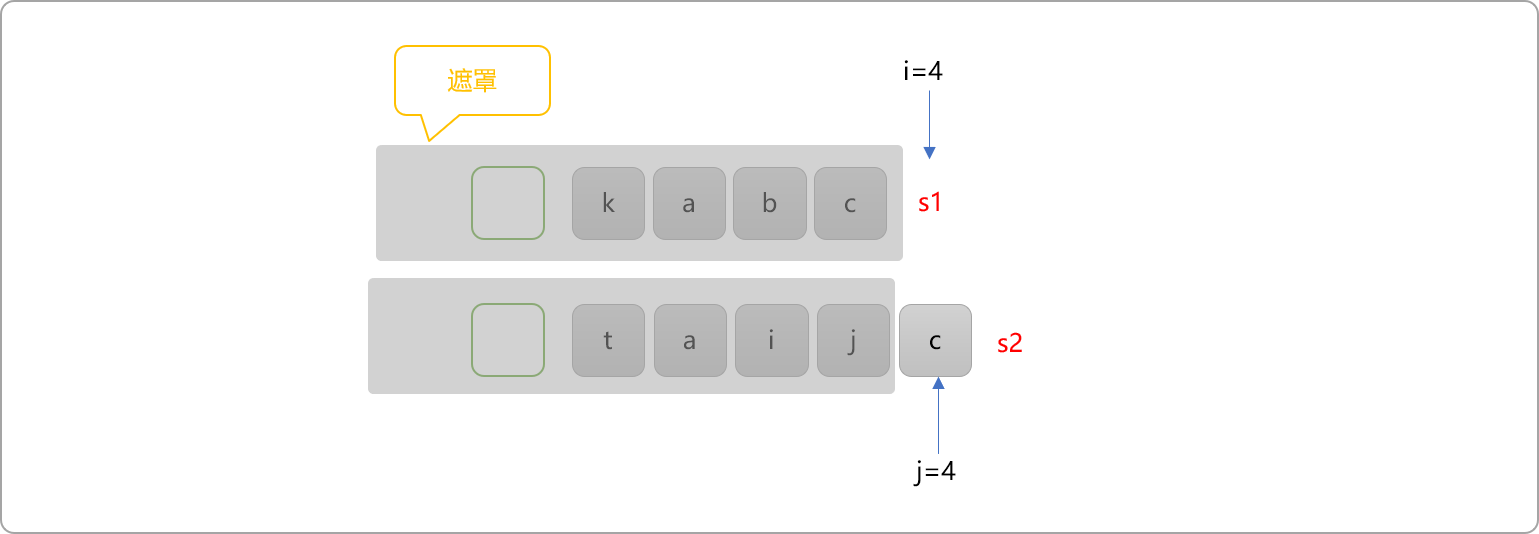
- 递归边界。当
i==s1.size() 或 j==s2.size()时,说明已经扫描到了子符串的最后。如下图所示,无论哪一个指针先到达字符串的末尾,则都不再存在任何公共子序列。
int lcs(string s1,int i,string s2,int j){if(i==s1.size() || j==s2.size())return 0;if(s1[i]!=s2[j]){//有 3 种选择int sel_1=lcs(s1,i,s2,j+1);int sel_2=lcs(s1,i+1,s2,j);int sel_3=lcs(s1,i+1,s2,j+1);//三者之中选择最大返回值}else{//只有一个选择return lcs(s1,i+1,s2,j+1)+1;}
}
上述是基于递归的角度分析问题,完整的代码如下:
#include <iostream>
using namespace std;
int lcs(string s1,int i,string s2,int j) {if(i==s1.size() || j==s2.size())return 0;if(s1[i]!=s2[j]) {//有 3 种选择int sel_1=lcs(s1,i,s2,j+1);int sel_2=lcs(s1,i+1,s2,j);int sel_3=lcs(s1,i+1,s2,j+1);int maxVal=max(sel_1,sel_2);maxVal=max(maxVal,sel_3);return maxVal;} else {//只有一个选择return lcs(s1,i+1,s2,j+1)+1;}
}
int main() {string s1,s2;cin>>s1>>s2;int res= lcs(s1,0,s2,0);cout<<res;return 0;
}
当字符串的长度较大时,基于递归的运算量会较大,问题在于递归算法中存在大量的重叠子问题。
2.3 重叠子问题
绘制递归树,可清晰看到重叠子问题的存在。
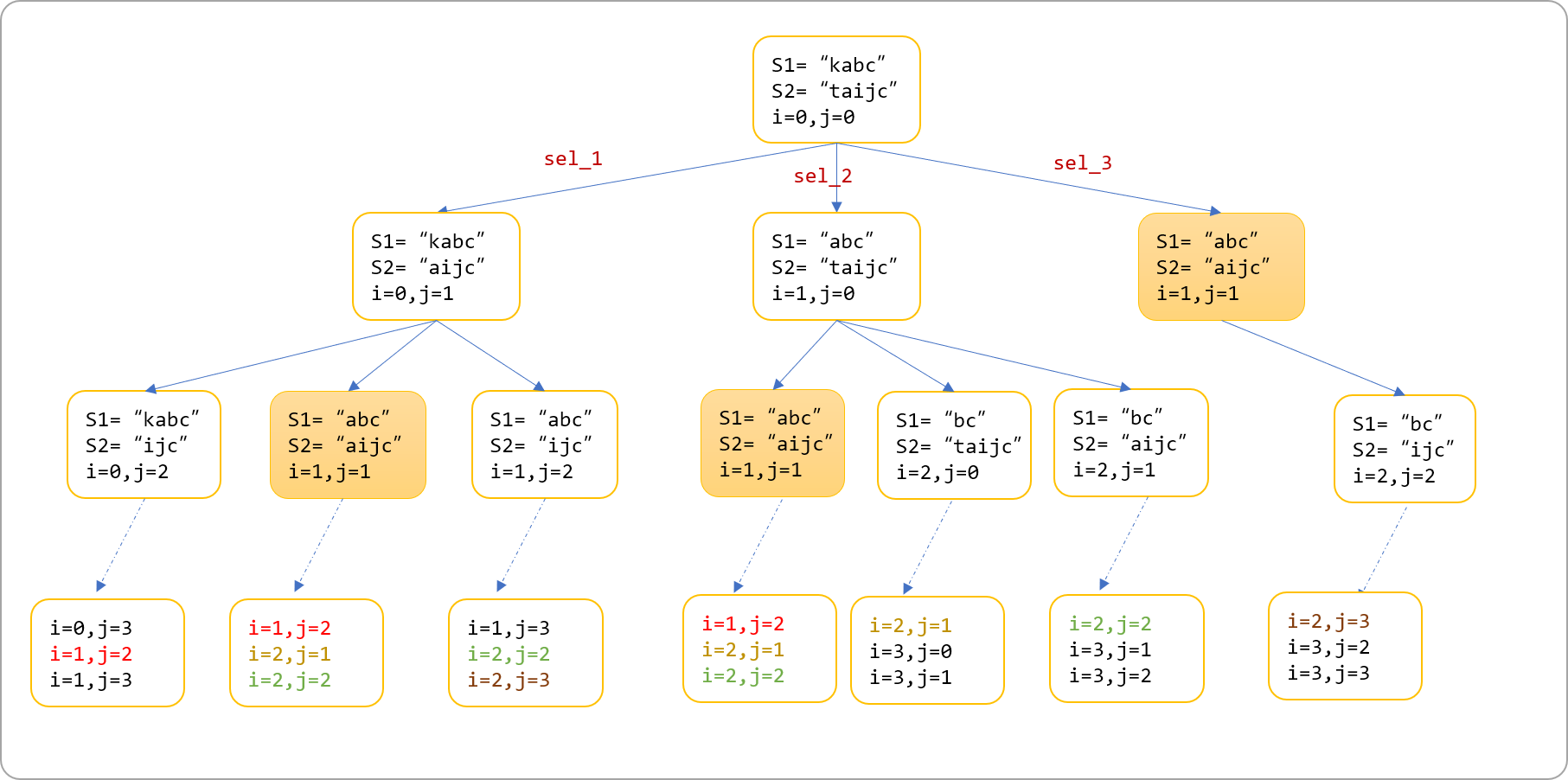
并且可以看到 sel_1和sel_2分支包括sel_3分支,可以使用缓存方案解决递归中的重叠子问题,让重叠子问题只被计算一次。完整代码如下 :
#include <iostream>
#include <map>
using namespace std;
//缓存
map<pair<int,int>,int> cache;
int lcs(string s1,int i,string s2,int j) {if(i==s1.size() || j==s2.size())return 0;pair<int,int> p= {i,j};if (cache[p] ) {return cache[p];}if(s1[i]!=s2[j]) {//有 3 种选择int sel_1=lcs(s1,i,s2,j+1);int sel_2=lcs(s1,i+1,s2,j);cache[p]=max(sel_1,sel_2);;} else {//只有一个选择cache[p]=lcs(s1,i+1,s2,j+1)+1;}return cache[p];
}
int main() {string s1,s2;cin>>s1>>s2;int res= lcs(s1,0,s2,0);cout<<res;return 0;
}
递归实现性能不可观,代码层面也稍显繁琐。类似于这样求最值的问题,可以试着使用动态规划来实现。
2.4 动态规划
递归解决问题的思想是由上向下,所谓由上向下,指先搁置规模较大的问题,等规模较小的子问题解决后再回溯出大问题的解。通过上文贴的递归树可以清晰看到求解流程。
动态规划的思想是由下向上,是基于枚举思想。记录每一个子问题的解,最终推导出比之更大问题的解。当然,要求小问题具有独立性和最优性。
无论由上向下,还是由下向上,其本质都是知道子问题答案后,再求解出大问题的答案。动态规划算法是直接了当,递归是迂回求解。
现以求字符串的最长公共子序列为例,讲解动态规划的求解过程。
构建dp数组,用来记录所有子问题的解,类似于递归实现的缓存器。 于本问题而言,dp是一个二维数组,理论上讲,从A推导出B,再从B推导出C……问题域关心的是最后的推导结论C,之前使用过的历史推导结论其实是可以不用存储。有点类似于"忘恩负义",所以可以对于dp数组进行压缩。
-
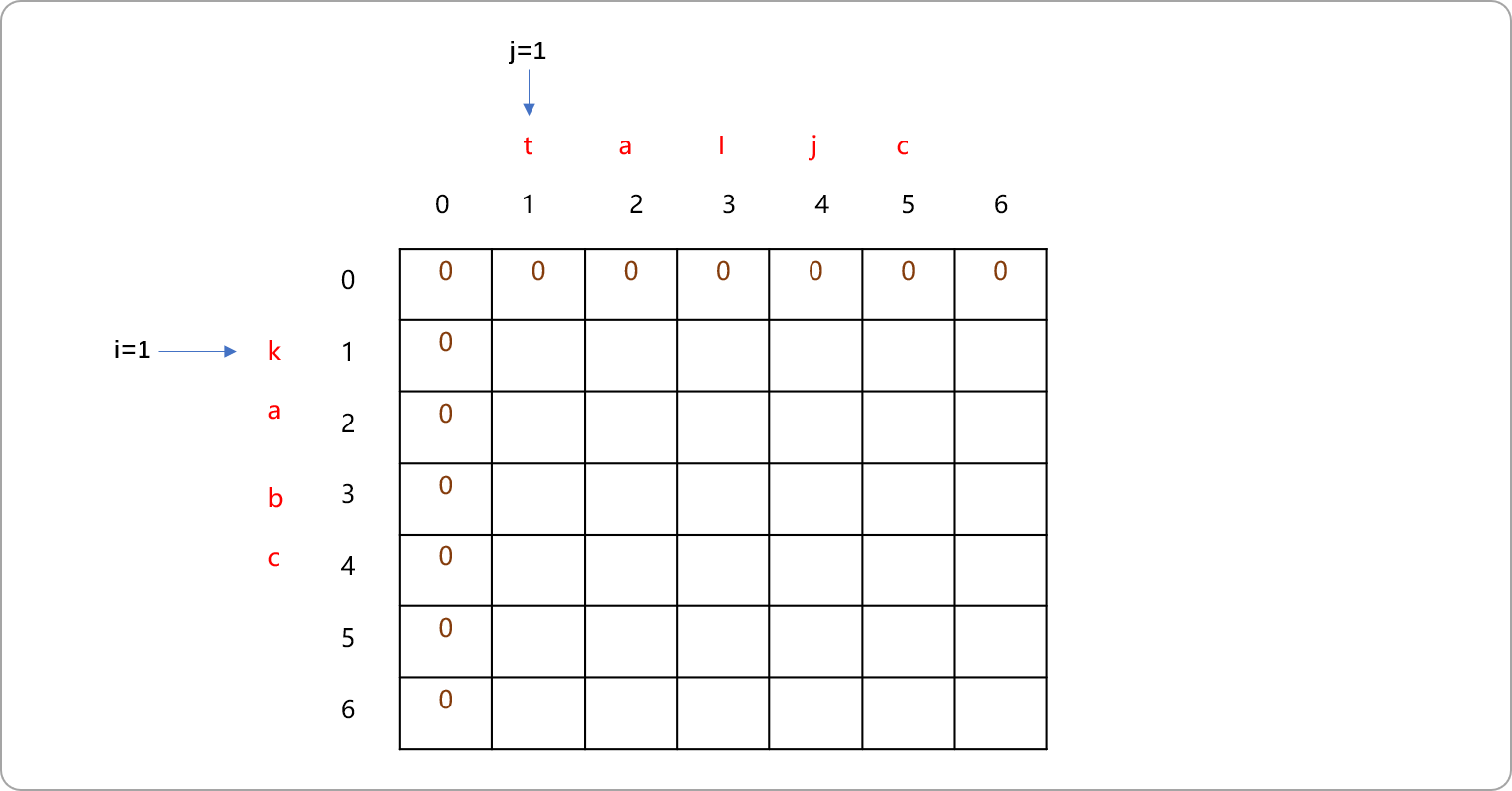
构建
dp二维数组。先初始化数组的第一行和第一列的值为0。推导必须有一个源头,这里的0就是源头。当
s1=""、s2="a……"或当s1="a……"、s2=""或当s1=""、s2=""时可认为最长公共子序列的值为0。
-
如图,让
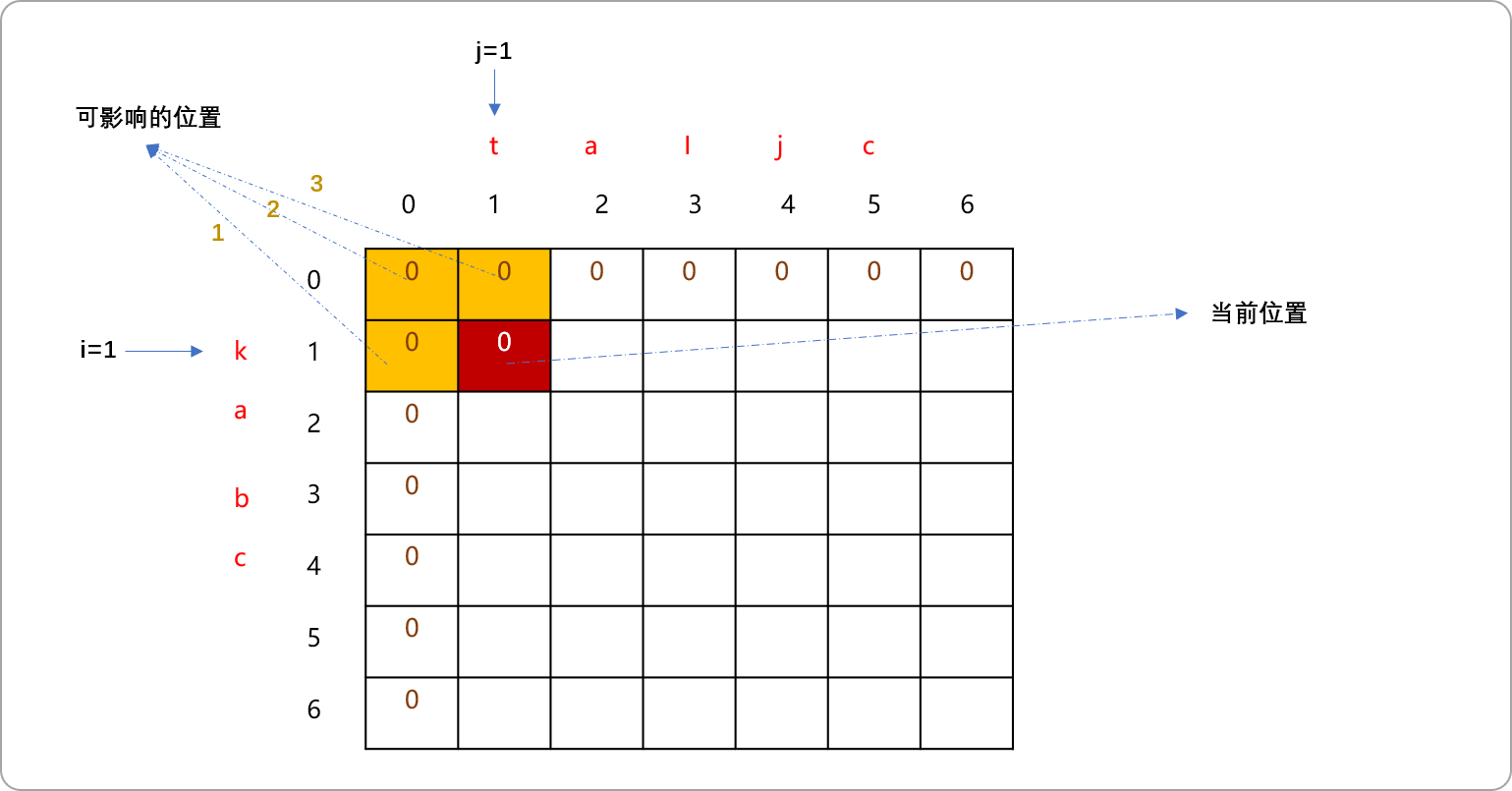
i=1、j=1,比较s1[i]和s2[j]位置的字符,显然k与t是不相等的。递归是看后面(还没求解)有多少个子问题可以选择,动态规划是看前面(已经求解)有多个子问题会影响当前子问题。对于当前位置而言,对之有影响的位置有3个。如下图标记为黄色区域位置。1位置坐标为(i,j-1)。表示s1中有k且s2中无t时最长公共子序列的值。2位置坐标为(i-1,j-1)。表示s1中无k且s2中无t时最长公共子序列的值。3位置坐标为(i-1,j)。表示s1中无k且s2中有t时最长公共子序列的值。
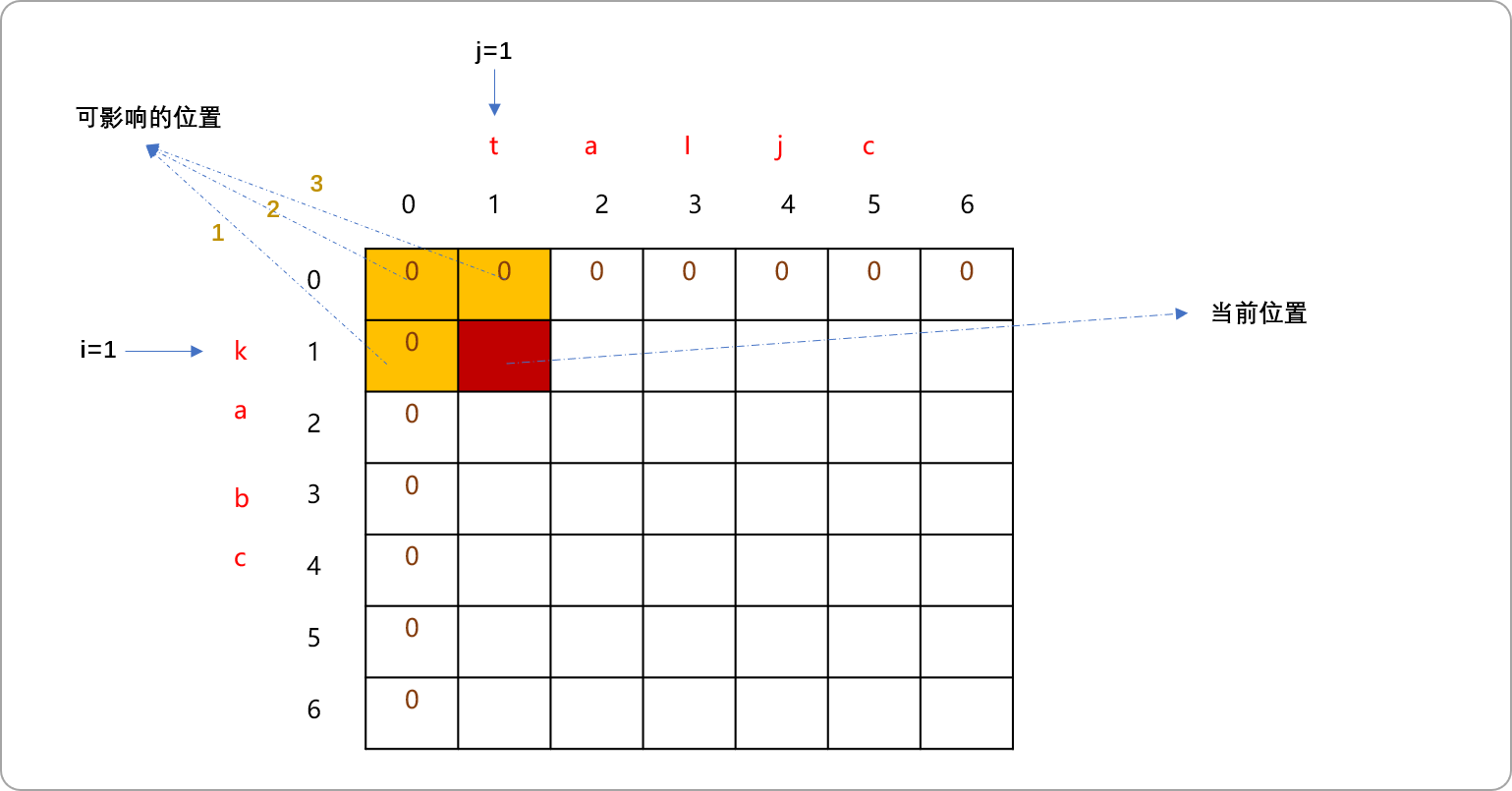
可以舍弃位置3,然后在位置1和位置2中求最大值。
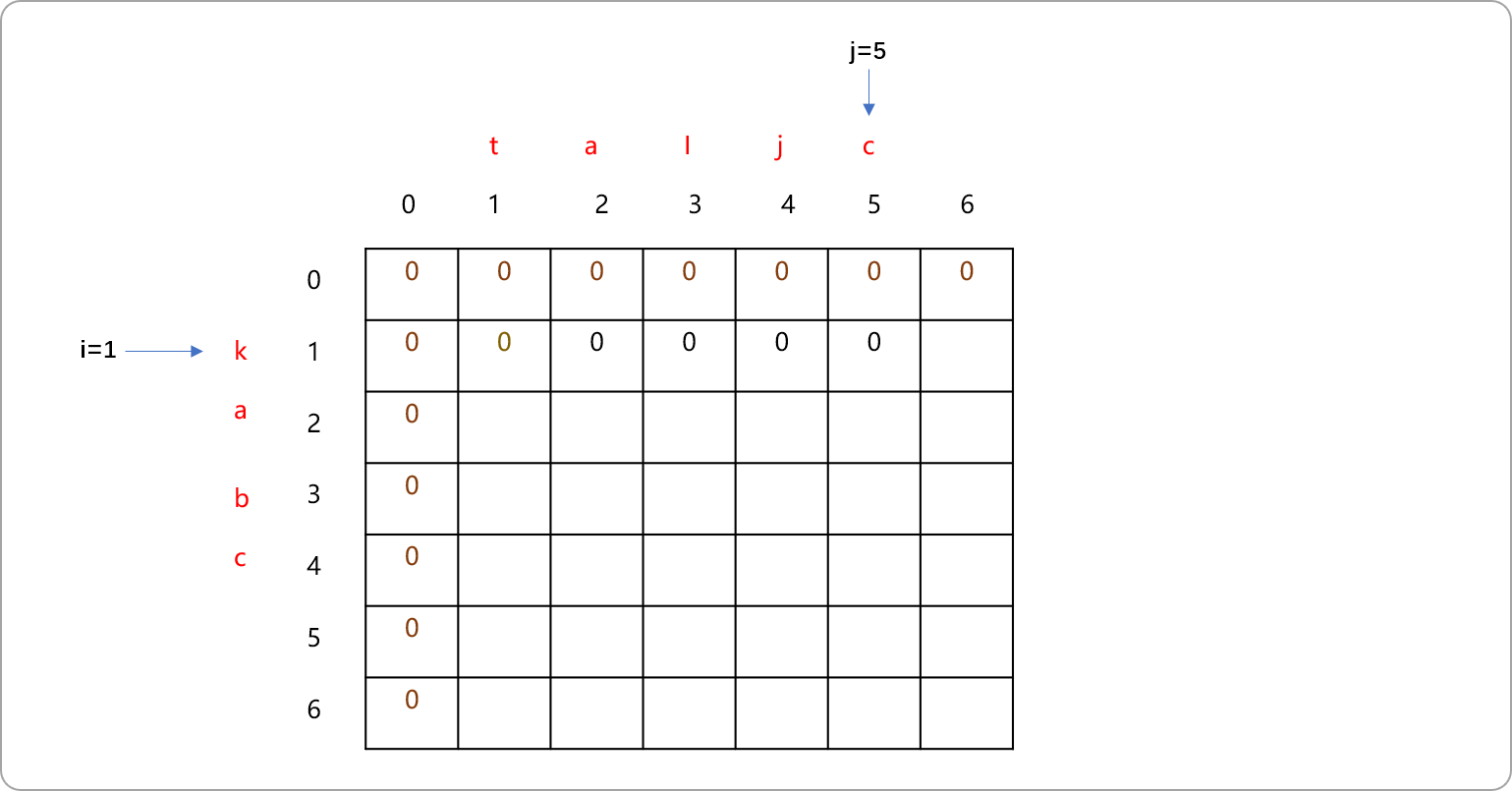
i=1不变,改成j的值。一路比较s1[i]和s2[j]中值,因都不相等,根据前面的分析,很容易填写出dp值。
-
移动
i=2,重置j=1且移动j。i和j所在位置的字符不相等时的问题已经分析。如下图,当
i=2,j=2时,s[i]和s[j]的值相等,则影响此位置值的前置位置应该是哪个?
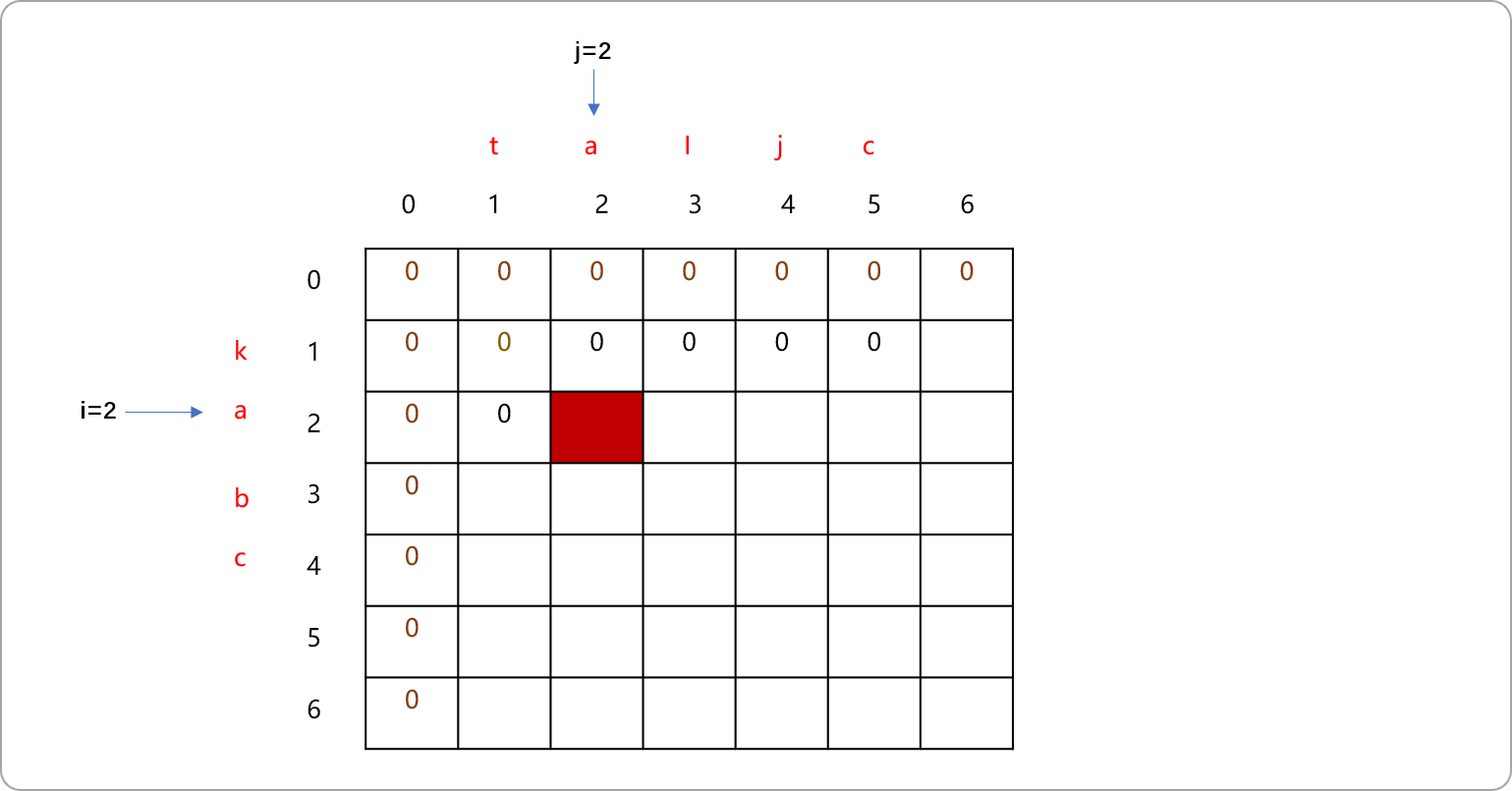
相等,显然最长公共子序列会增加1,问题是在哪一个前置子问题的值上加 1?
其实,只需要在如下黄色区域位置的值上加上1,此位置表示当s1和s2中都没有a的时候。
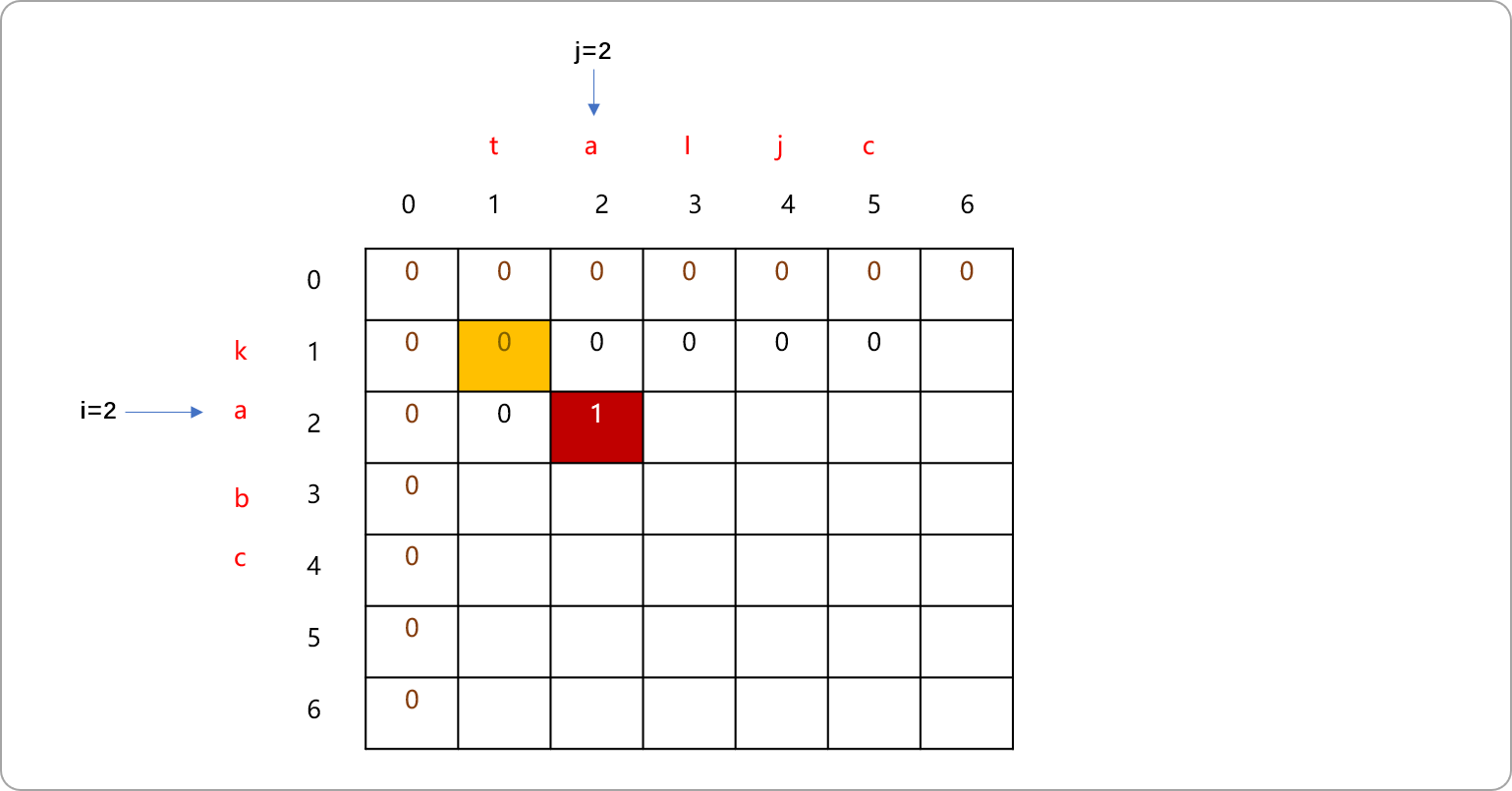
- 按如上分析原理,可以把整个
dp表填写完成。
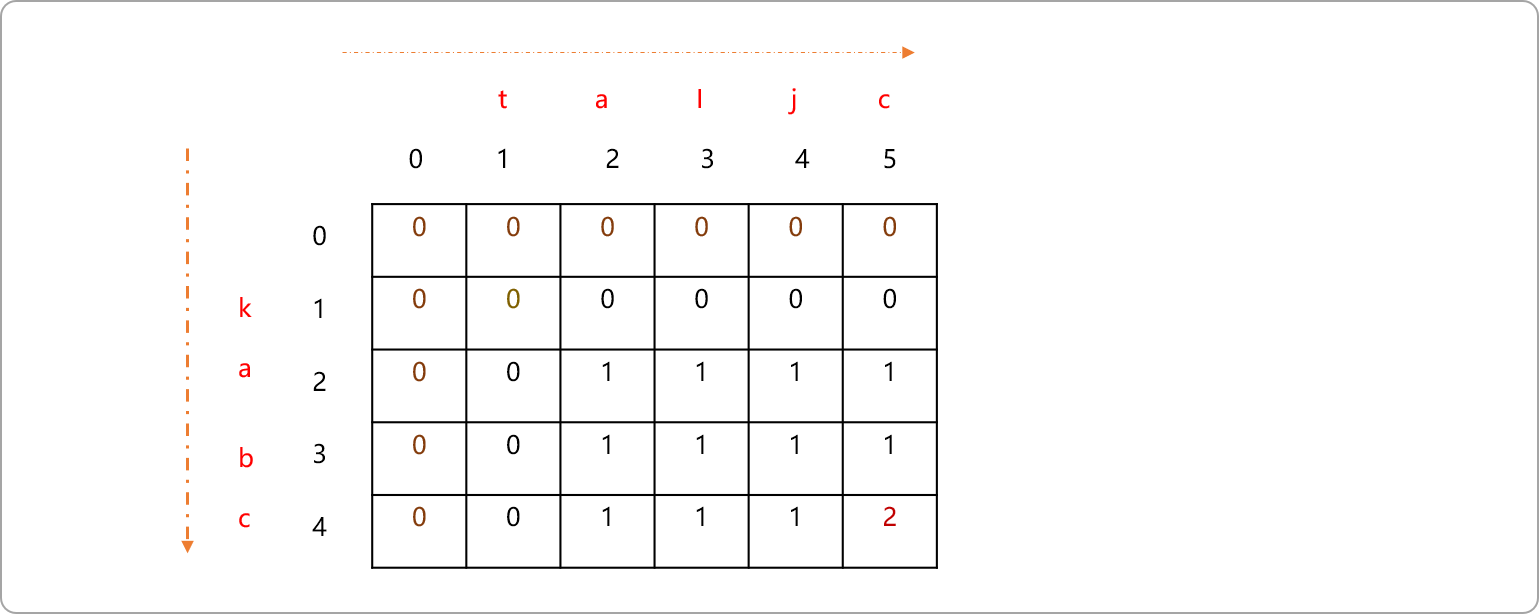
编码实现:
#include <iostream>
#include <map>
using namespace std;
int dp[100][100]= {0};
void lcs(string s1,string s2) {//初始化动态规划表for(int i=0; i<s2.size(); i++)dp[0][i]=0;for(int i=0; i<s1.size(); i++)dp[i][0]=0;for(int i=1; i<=s1.size(); i++) {for(int j=1; j<=s2.size(); j++)if(s1[i-1]==s2[j-1]) {//相等dp[i][j]=dp[i-1][j-1]+1;} else {dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}
}
int main() {string s1,s2;cin>>s1>>s2;lcs(s1,s2);for(int i=0; i<=s1.size(); i++) {for(int j=0; j<=s2.size(); j++) {cout<<dp[i][j]<<"\t";}cout<<endl;}cout<<"最长公共子序列:"<<endl;int res=dp[s1.size()][s2.size()];cout<<res<<endl;return 0;
}
测试结果:
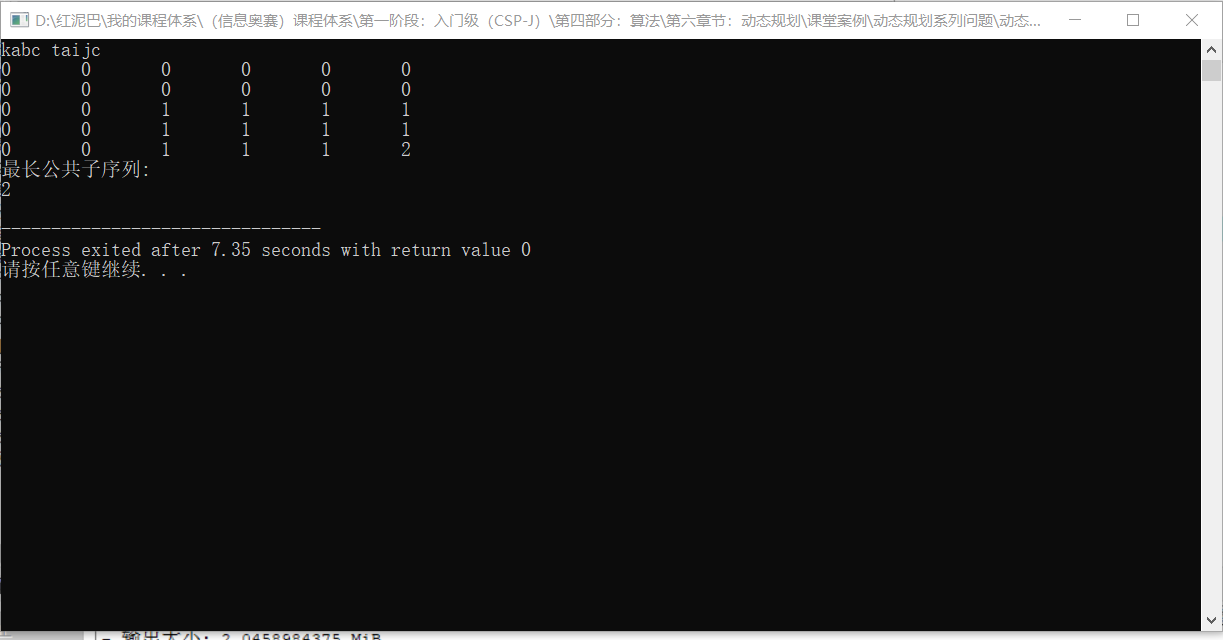
4. 总结
最长公共子序列很有代表性,分析基于递归和动态规划的实现过程,可以帮助我们理解此类问题,且解决此类问题。
相关文章:

C++ 动态规划经典案例解析之最长公共子序列(LCS)_窥探递归和动态规划的一致性
1. 前言 动态规划处理字符相关案例中,求最长公共子序列以及求最短编辑距离,算是经典中的经典案例。 讲解此类问题的算法在网上一抓应用一大把,即便如此,还是忍不住有写此文的想法。毕竟理解、看懂都不算是真正掌握,唯…...

接口测试自动化:简化测试流程,提升效率
接口测试自动化:简化测试流程,提升效率 什么是接口测试自动化? 接口测试自动化是指使用特定的工具和技术来自动化执行接口测试的过程。通过编写脚本,自动化工具可以模拟用户与软件系统的交互,验证接口的功能和性能。…...
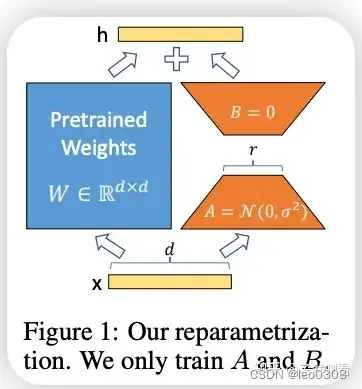
LoRA微调方法详解
本文要介绍的是大模型的微调训练方法之一----LoRA。 0 背景 现在大模型非常火爆,大家都在想方设法应用大模型。 当前很多大模型虽说可以zero-shot直接使用, 但是在具体应用上一般还是微调一下效果更好, 也就是常说的finetune。 在小模型时代…...
redis-数据类型及样例
一.string 类型数据的基本操作 1.添加/修改数据 set key value2.获取数据 get key3.删除数据 del key4.添加/修改多个数据 mset key1 value1 key2 value25.获取多个数据 mget key1 key2二.list类型的基本操作 数据存储需求:存储多个数据,并对数据…...

公司电脑三维图纸加密、机械图挡加密软件
机械图纸加密软件的问世,让很多的网络公司都大受其带来的工作中的便利。在安装了机械图纸加密软件后,不仅可以很好的管理员工在工作时的上网娱乐,在对整个公司员工的工作效率上也有着明显的提高,那么对于机械图纸加密软件的具体特…...
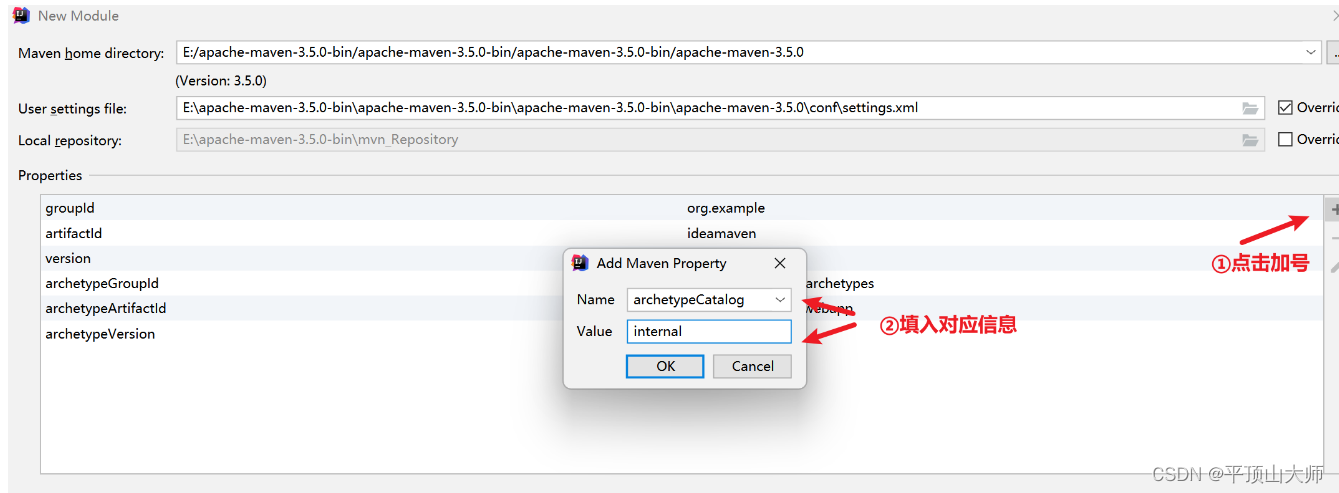
安装使用IDEA,修改样式,配置服务,构建Maven项目(超级详细版)
目录 前言: 一,安装 1.1打开官网JetBrains: Essential tools for software developers and teams点击 Developer Tools,再点击 Intellij IDEA 2.点击下载编辑 3.选择对应的版本,左边的 Ultimate 版本为旗舰版,需要…...
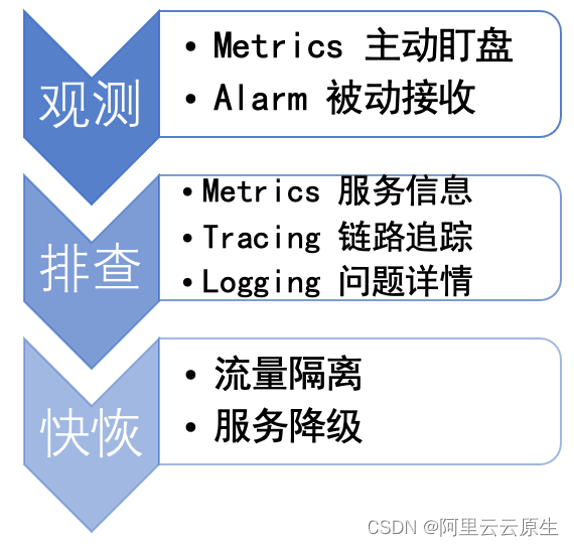
Apache Dubbo 云原生可观测性的探索与实践
作者:宋小生 - 平安壹钱包中间件资深工程师 Dubbo3 可观测能力速览 Apache Dubbo3 在云原生可观测性方面完成重磅升级,使用 Dubbo3 最新版本,你只需要引入 dubbo-spring-boot-observability-starter 依赖,微服务集群即原生具备以…...
DaVinci Resolve Studio 18 for Mac 达芬奇调色
DaVinci Resolve Studio 18是一款专业的视频编辑和调色软件,适用于电影、电视节目、广告等各种视觉媒体的制作。它具有完整的后期制作功能,包括剪辑、调色、特效、音频处理等。 以下是DaVinci Resolve Studio 18的主要特点: - 提供了全面的视…...

Excelize Go语言操作 Office Excel文档基础库
Excelize 是 Go 语言编写的用于操作 Office Excel 文档基础库,基于 ECMA-376,ISO/IEC 29500 国际标准。可以使用它来读取、写入由 Microsoft Excel™ 2007 及以上版本创建的电子表格文档。支持 XLAM / XLSM / XLSX / XLTM / XLTX 等多种文档格式…...

SpringBoot、Java 使用 Jsoup 解析 HTML 页面
使用 Jsoup 解析 HTML 页面 什么是 Jsoup? Jsoup 是一个用于处理 HTML 页面的 Java 库,它提供了简单的 API,使得从 HTML 中提取数据变得非常容易。无论是获取特定标签的内容还是遍历整个页面的元素,Jsoup 都能轻松胜任。 如何使…...

C# 随心记
#region 批量保存到数据库 public bool InsertDB(DataTable dt) { bool bResult true; LogInfo.WriteTextToFile("使用Bulk插入的实现方式"); Stopwatch sw new Stopwatch(); using (SqlConnecti…...

华为OD机试-字符串分割
题目描述 给定一个非空字符串S,其被N个‘-’分隔成N1的子串,给定正整数K,要求除第一个子串外,其余的子串每K个字符组成新的子串,并用‘-’分隔。对于新组成的每一个子串,如果它含有的小写字母比大写字母多…...

element-ui的el-dialog,简单的封装。
el-dialog是使用率很高的组件 使用el-dialog很多都是按照文档的例子,用一个变量控制是否显示,再来一个变量控制标题。 如果我这个对话框多个地方使用的话还要创建多个变量,甚至关闭之后还要清空一些变量,应该可以简化一点。我写…...
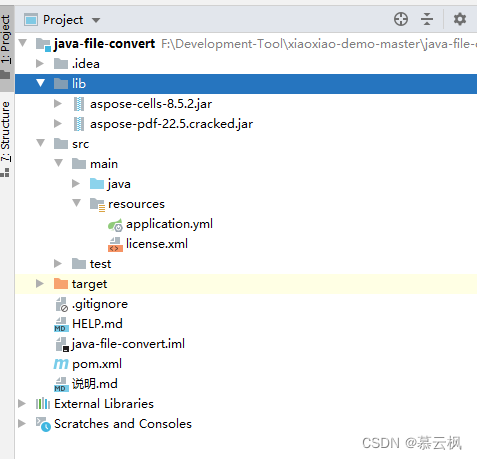
SpringBoot引入外部jar打包失败解决,SpringBoot手动引入jar打包war后报错问题
前言 使用外部手动添加的jar到项目,打包时出现jar找不到问题解决 处理 例如项目结构如下 引入方式换成这种 <!-- 除了一下这两种引入外部jar,还是可以将外部jar包添加到maven中(百度查)--><!-- pdf转word --><…...

HTTP基础:学习HTTP协议的基本知识,了解请求和响应的过程
HTTP(Hypertext Transfer Protocol,超文本传输协议)是一种用于传输超媒体文档(如HTML)的应用层协议,它是Web中最基本的协议。 HTTP请求和响应都是由客户端和服务器之间进行的。 一个完整的HTTP请求由以下几…...

Spark基础-任务提交相关参数
整理一下用过的spark相关的参数 spark应用提交命令spark-submit的常用参数(使用spark-submit --help可以查看所有参数, 有一些参数在下面的spark配置属性定义了,也没有额外列出) 参数默认值含义--master local[*]spark集群的mast…...
ROS-PyQt小案例
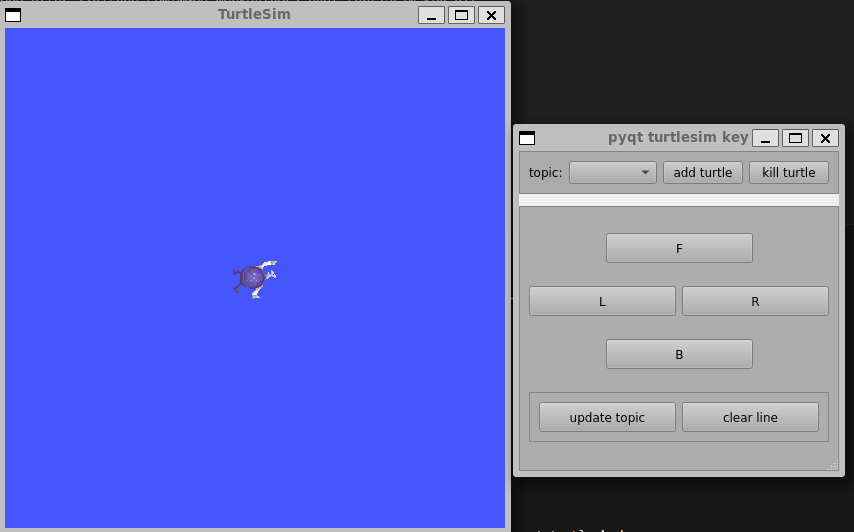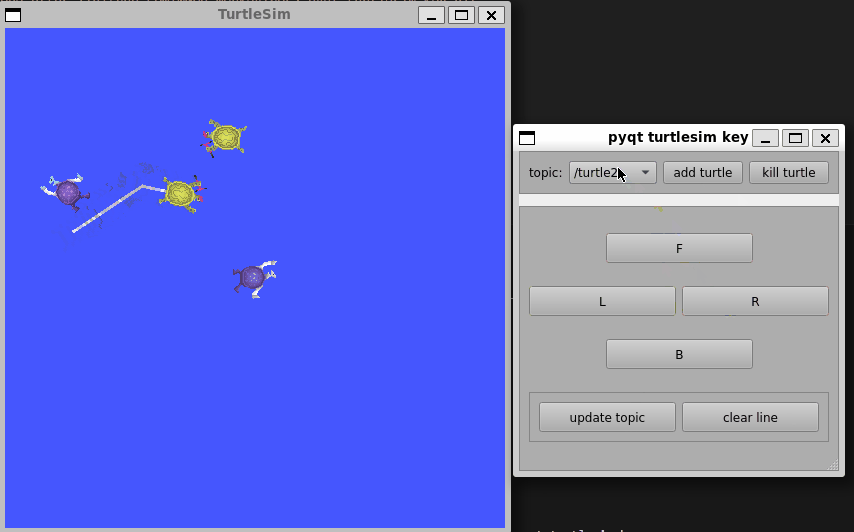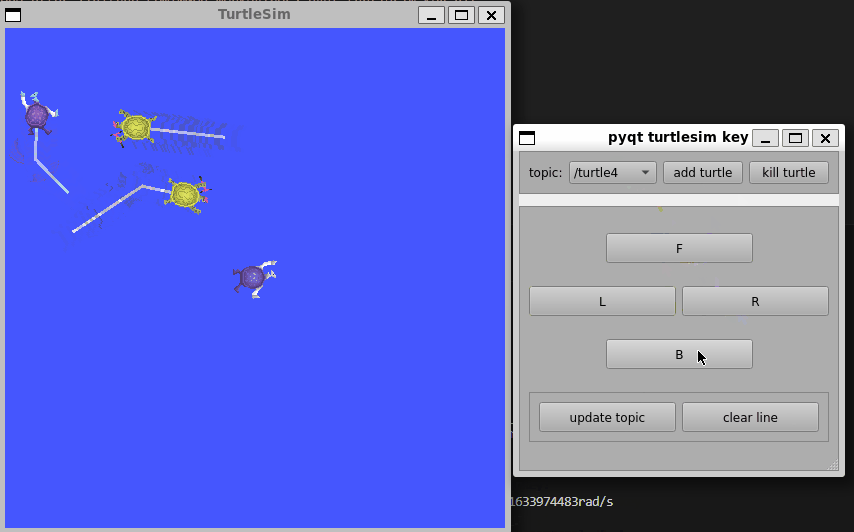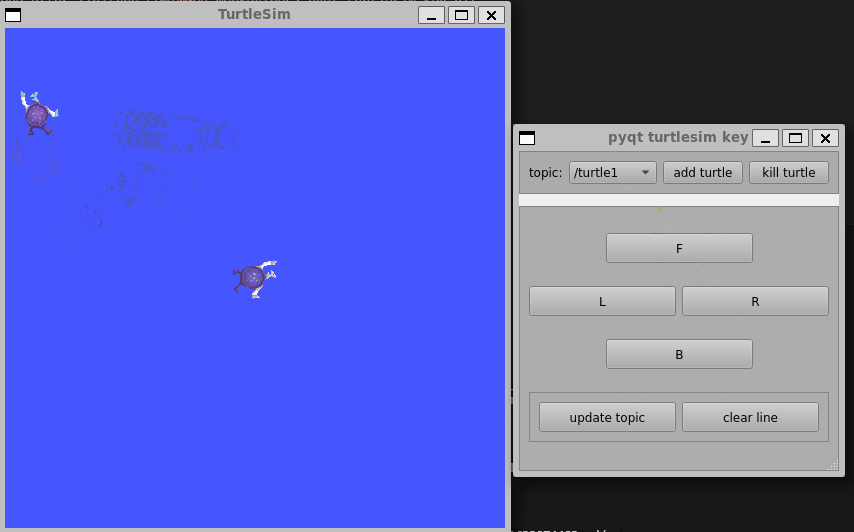
前言:目前还在学习ROS无人机框架中,,, 更多更新文章详见我的个人博客主页【前往】 ROS与PyQt5结合的小demo,用于学习如何设计一个界面,并与ROS中的Service和Topic结合,从而控制多个小乌龟的运动…...
【算法】双指针——leetcode盛最多水的容器、剑指Offer57和为s的两个数字
盛水最多的容器 (1)暴力解法 算法思路:我们枚举出所有的容器大小,取最大值即可。 容器容积的计算方式: 设两指针 i , j ,分别指向水槽板的最左端以及最右端,此时容器的宽度为 j - i 。由于容器…...
idea 使用debug 启动项目的时候 出现 Method breakpoints may dramatically slow down debugging
问题: 1. 写了一段时间的代码,在debug启动项目后提示:Method breakpoints may dramatically slow down debugging 但是正常启动是可以的,debug不行。 2. idea 里面的项目,很多地方都有断点,现在想要取消全部的断点…...
Tomcat的一些配置问题(server.xml/catalina.sh)
在同一机器中运行多个Tomcat时,如果不修改server.xml的端口参数,会出现端口冲突使得Tomcat异常;Tomcat默认配置中,JAVA_OPTS不会设置太大,一般需要在catalina.sh中增加一行配置来加大该参数值。 目录 1.Server.xml配置…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
