多层感知机
多层感知机理论部分
本文系统的讲解多层感知机的pytorch复现,以及详细的代码解释。
部分文字和代码来自《动手学深度学习》!!
目录
- 多层感知机理论部分
- 隐藏层
- 多层感知机数学逻辑
- 激活函数
- 1. ReLU函数
- 2. sigmoid函数
- 3. tanh函数
- 多层感知机的从零开始实现
- 数据集
- 初始化参数模型
- 激活函数
- 模型定义
- 损失函数
- 训练
- 多层感知机的pytorch实现(pytorch实现神经网络的流程)
- 1. 数据集
- 模型定义及参数初始化
- 损失函数,优化器和超参数的定义
- tensorboard的初始化
- 训练
- 预测
- 模型的保存与获取
隐藏层
上两节我们使用的网络都是线性的,即只有输入层和输出层两层,但生活中线性模型有很大的限制。例如,如何对猫和狗的图像进行分类呢? 增加位置处像素的强度是否总是增加(或降低)图像描绘狗的似然? 对线性模型的依赖对应于一个隐含的假设, 即区分猫和狗的唯一要求是评估单个像素的强度。 在一个倒置图像后依然保留类别的世界里,这种方法注定会失败。
所以我们在网络中加入隐藏层来克服线性模型的限制,使其能更普遍的处理函数关系模型。
要做到这一点,最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出。 我们可以把前层看作表示,把最后一层看作线性预测器。 这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP。像下面的图示:
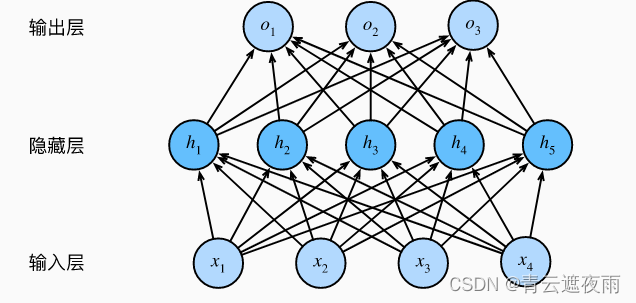
这个多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元。 输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算。 因此,这个多层感知机中的层数为2。 注意,这两个层都是全连接的。 每个输入都会影响隐藏层中的每个神经元, 而隐藏层中的每个神经元又会影响输出层中的每个神经元。
多层感知机数学逻辑
多层感知机(Multilayer Perceptron, MLP)是一种基于多个全连接层的前馈神经网络,其公式如下:
假设输入为 x∈Rd\boldsymbol{x} \in \mathbb{R}^dx∈Rd,第 iii 个全连接层的权重和偏差参数为 Wi∈Rhi−1×hi\boldsymbol{W}i \in \mathbb{R}^{h{i-1}\times h_i}Wi∈Rhi−1×hi 和 bi∈R1×hi\boldsymbol{b}_i \in \mathbb{R}^{1\times h_i}bi∈R1×hi,激活函数为 ϕi(⋅)\phi_i(\cdot)ϕi(⋅)。输出为 o∈Rq\boldsymbol{o} \in \mathbb{R}^{q}o∈Rq,则有:
h0=xhi=ϕi(hi−1Wi+bi),i=1,2,…,n−1o=hn−1Wn+bn\begin{aligned} \boldsymbol{h}_0 &= \boldsymbol{x} \\ \boldsymbol{h}i &= \phi_i(\boldsymbol{h}_{i-1} \boldsymbol{W}_i + \boldsymbol{b}i), \quad i=1,2,\ldots,n-1\\ \boldsymbol{o} &= \boldsymbol{h}_{n-1} \boldsymbol{W}_n + \boldsymbol{b}_n \end{aligned} h0hio=x=ϕi(hi−1Wi+bi),i=1,2,…,n−1=hn−1Wn+bn
其中 nnn 表示全连接层数,hi\boldsymbol{h}_ihi 表示第 iii 层的输出,h0\boldsymbol{h}_0h0 为输入,Wn∈Rhn−1×q\boldsymbol{W}n \in \mathbb{R}^{h{n-1}\times q}Wn∈Rhn−1×q 和 bn∈R1×q\boldsymbol{b}_n \in \mathbb{R}^{1\times q}bn∈R1×q 是输出层的权重和偏差参数。hih_ihi 表示第 iii 层的输出维度,也就是该层的神经元个数。最后一层的激活函数一般不加,也可以视为 ϕn(⋅)=identity(⋅)\phi_n(\cdot) = \mathrm{identity}(\cdot)ϕn(⋅)=identity(⋅)。
激活函数
激活函数将非线性特性引入到神经网络中。在下图中,输入的 inputs 通过加权,求和后,还被作用了一个函数f,这个函数f就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
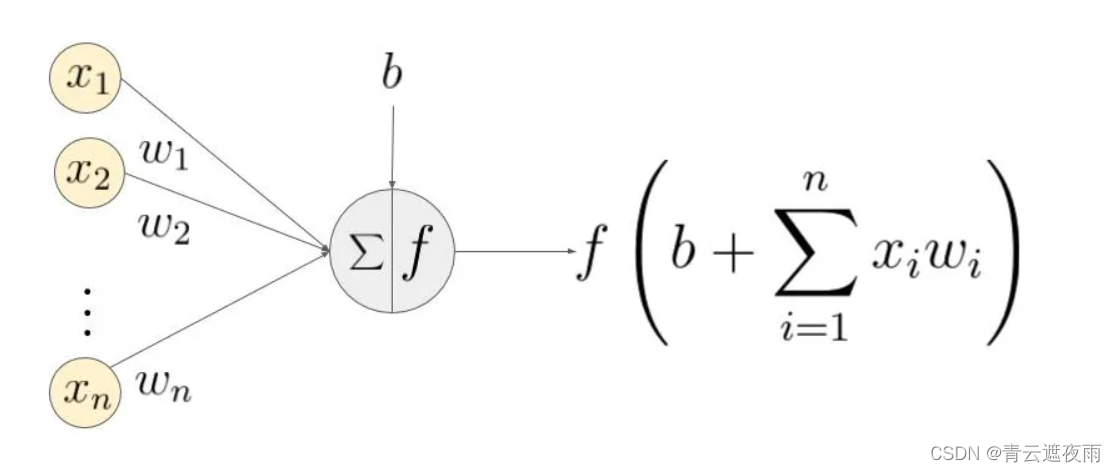
为什么使用激活函数
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
1. ReLU函数
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU), 因为它实现简单,同时在各种预测任务中表现良好。 ReLU提供了一种非常简单的非线性变换。 给定元素x,ReLU函数被定义为该元素与的0最大值:
ReLU(x)=max(x,0)ReLU(x) = max(x, 0)ReLU(x)=max(x,0)
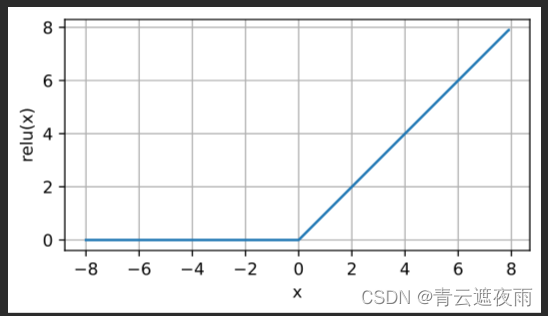
通俗地说,ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。 为了直观感受一下,我们可以画出函数的曲线图。 正如从图中所看到,激活函数是分段线性的。
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
 、
、
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。 注意,当输入值精确等于0时,ReLU函数不可导。 在此时,我们默认使用左侧的导数,即当输入为0时导数为0。 我们可以忽略这种情况,因为输入可能永远都不会是0。
观察其求导图像
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
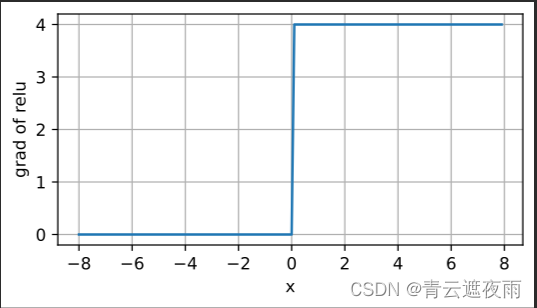
观察图像可知,它求导表现得特别好:要么让参数消失,要么让参数通过。 这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题
2. sigmoid函数
sigmoid函数是一种常用的激活函数,是早期深度学习和神经网络研究比较常用的激活函数,但在现在使用较少,其常用于神经网络的输出层,将输入的值映射到[0, 1]区间内,公式如下:
sigmoid(x)=11+exp(−x)sigmoid(x)=\frac{1}{1+exp(-x)}sigmoid(x)=1+exp(−x)1
图像为:
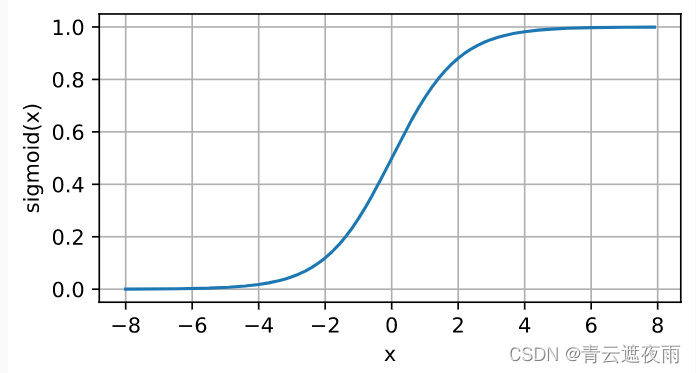
其中,x为输入值。sigmoid函数的输出值范围在(0, 1)之间,当x为0时,sigmoid函数的值为0.5。sigmoid函数的导数可以用其自身表示:
σ(x)=11+e−xddxσ(x)=e−x(1+e−x)2&=11+e−x⋅e−x1+e−x=σ(x)(1−σ(x))\begin{aligned}\sigma(x) & =\frac{1}{1+e^{-x}} \ \frac{d}{dx} \sigma(x) &= \frac{e^{-x}}{(1+e^{-x})^2}\&=\frac{1}{1+e^{-x}}\cdot \frac{e^{-x}}{1+e^{-x}} \ &=\sigma(x)(1-\sigma(x))\end{aligned}σ(x)=1+e−x1 dxdσ(x)=(1+e−x)2e−x&=1+e−x1⋅1+e−xe−x =σ(x)(1−σ(x))
sigmoid函数具有连续可导、单调递增、输出值在(0, 1)之间等特点,但其缺点也比较明显,如当输入值过大或过小时,其导数趋于0,容易出现梯度消失的问题。
感兴趣的同学可以参照上面的代码自行绘制sigmoid函数导数的图像
3. tanh函数
tanh函数是双曲正切函数(hyperbolic tangent function)的缩写,数学表达式为:tanh(x)=1−e−2x1+e−2x\text{tanh}(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}}tanh(x)=1+e−2x1−e−2x
图像为:
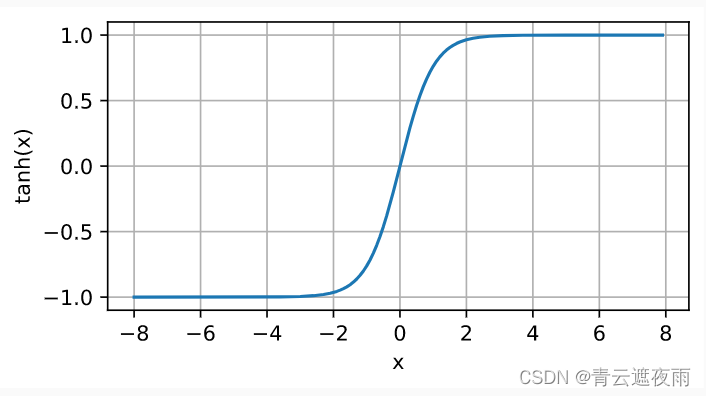
与sigmoid函数类似,tanh函数也是一种常用的激活函数。它的取值范围为 (−1,1)(-1, 1)(−1,1),且在原点处取值为0。相比于sigmoid函数,在输入接近0的时候,tanh函数的函数值变化更为明显,可以使得模型更快地学习到特征。同时,tanh函数在原点两侧的函数值的变化也更加平缓,避免了在输入较大或较小的时候出现梯度消失的问题。
其导数为:
ddxtanh(x)=1−tanh2(x)\frac{d}{dx}\operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x) dxdtanh(x)=1−tanh2(x)
多层感知机的从零开始实现
数据集
我们同样使用fashion-MNIST数据集,为了与上一节softmax回归做对比,理解线性和非线性之间的差别。
import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
注:load_data_fashion_mnist函数在上一节实现过,这里我们直接调用李沐大佬做的d2l包中的函数,源码在上一节。
初始化参数模型
回想一下,Fashion-MNIST中的每个图像由784个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构, 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 首先,我们将实现一个具有单隐藏层的多层感知机, 它包含256个隐藏单元。 注意,我们可以将这两个变量都视为超参数。 通常,我们选择2的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式,这么做往往可以在计算上更高效。
为了简化代码,我们实现三层的感知机,故参数为输入层到隐藏层的W1,b1和隐藏层到输出层的W2,b2
num_inputs, num_outputs, num_hiddens = 784, 10, 256W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))params = [W1, b1, W2, b2]
Parameter 是一个 Tensor 的子类,在定义神经网络时常用于将需要优化的参数包裹在其中。与普通的 Tensor 不同, Parameter 会被自动添加到模型的参数列表中,以便在反向传播过程中自动求导更新参数。当我们在使用优化算法训练模型时,我们只需要调用模型的 parameters() 方法即可获得所有需要优化的参数。
torch.randn(num_inputs, num_hiddens, requires_grad=True) 生成了一个大小为 (num_inputs, num_hiddens) 的张量,表示输入和隐藏层之间的权重。由于该张量是需要被优化的,因此 requires_grad=True 表示该张量的导数需要被计算和存储,以便在反向传播中计算梯度。
生成的随机数乘以 0.01 的目的是将其缩小,从而避免初始参数值过大,导致神经网络训练过程中出现梯度消失或爆炸的问题。
激活函数
def relu(X):a = torch.zeros_like(X)return torch.max(X, a)
模型定义
def net(X):X = X.reshape((-1, num_inputs))H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法return (H@W2 + b2)
损失函数
我们采用交叉熵作为损失函数
loss = nn.CrossEntropyLoss(reduction='none')
训练
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
其中train_ch3的实现部分在上一节
多层感知机的pytorch实现(pytorch实现神经网络的流程)
1. 数据集
import torch
from torch import nn
from d2l import torch as d2l
import torchvision
from torch.utils import data
from torchvision import transforms
def get_dataloader_workers(): #@save"""使用4个进程来读取数据"""return 4def load_data_fashion_mnist(batch_size, resize=None): #@save"""下载Fashion-MNIST数据集,然后将其加载到内存中"""trans = [transforms.ToTensor()]if resize:trans.insert(0, transforms.Resize(resize))trans = transforms.Compose(trans)mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)return (data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers()),data.DataLoader(mnist_test, batch_size, shuffle=False,num_workers=get_dataloader_workers()))
模型定义及参数初始化
net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),nn.Linear(256, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights);
损失函数,优化器和超参数的定义
loss = torch.nn.CrossEntropyLoss()#损失函数
lr = 0.01#学习率
optim = torch.optim.SGD(net.parameters(),lr=lr)#优化器
epoch = 10
batch_size=256
tensorboard的初始化
tensorboard用于存储和可视化损失函数和精确度等数据
from torch.utils.tensorboard import SummaryWriter
log_dir = ''
writer = SummaryWriter(log_dir)
训练
train_iter, test_iter = load_data_fashion_mnist(batch_size)
train_step = 0 #每轮训练的次数
net.train()#模型在训练状态
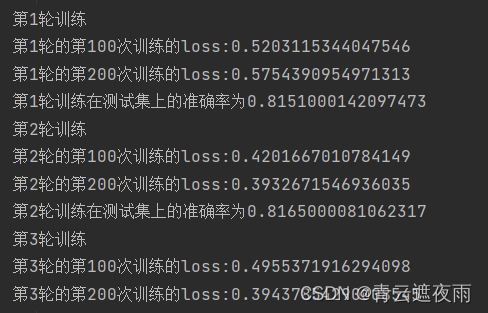
for i in range(epoch):print("第{}轮训练".format(i+1))train_step = 0total_loss = 0.0#总损失total_correct = 0#总正确数total_examples = 0#总训练数for X,y in train_iter:# 前向传播output=net(X)l=loss(output,y)# 反向传播和优化optim.zero_grad()l.backward()optim.step()#记录/输出损失和精确率total_loss += l.item()total_correct += (output.argmax(dim=1) == y).sum().item()total_examples += y.size(0)# 记录训练损失和准确率到 tensorboardwriter.add_scalar('train/loss', l.item(), epoch * len(train_iter) + i)writer.add_scalar('train/accuracy', total_correct/total_examples, epoch * len(train_iter) + i)train_step+=1if(train_step%100==0):#每训练一百组输出一次损失print("第{}轮的第{}次训练的loss:{}".format((i+1),train_step,l.item()))# 在测试集上面的效果net.eval() #在验证状态total_test_correct = 0total_test_examples = 0with torch.no_grad(): # 验证的部分,不是训练所以不要带入梯度for X,y in test_iter:outputs = net(X)test_result_loss=loss(outputs,y)total_test_correct += (outputs.argmax(1)==y).sum()total_test_examples += y.size(0)print("第{}轮训练在测试集上的准确率为{}".format((i+1),(total_test_correct/total_test_examples)))
这段代码是用于训练和测试深度学习模型的代码。首先使用 load_data_fashion_mnist(batch_size) 函数载入了Fashion-MNIST数据集并将训练数据和测试数据分别封装成 train_iter 和 test_iter 迭代器。
然后,将模型设置为训练状态:net.train()。接下来,开始训练模型。epoch 表示要迭代的轮数,外层循环控制训练轮数。内层循环遍历 train_iter 迭代器中的所有数据,并通过前向传播和反向传播更新模型参数。
在训练过程中,通过 total_loss、total_correct 和 total_examples 分别记录总的损失值、总的正确预测数量和总的样本数量,用于计算训练过程中的损失值和精确度。同时,将训练损失和准确率写入 tensorboard 中,以便后续可视化分析。
每训练一百次,将当前训练的损失值输出显示。
在训练完一轮后,使用 net.eval() 将模型转换为测试状态。在 with torch.no_grad() 的上下文管理器中,遍历 test_iter 迭代器中的所有测试数据,并通过模型进行预测,计算总的正确预测数量和总的样本数量,以计算测试准确率。最后,输出该轮训练在测试集上的准确率。
结果:
预测
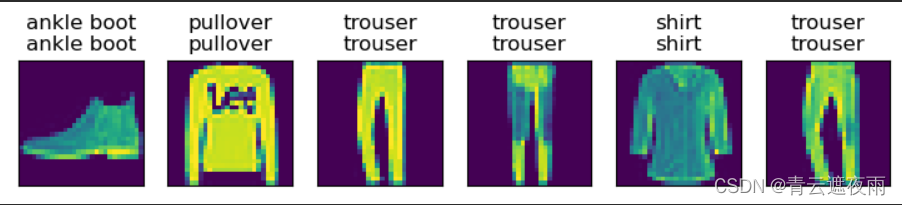
def predict(net, test_iter, n=6): #@savefor X, y in test_iter:breaktrues = d2l.get_fashion_mnist_labels(y)preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))titles = [true +'\n' + pred for true, pred in zip(trues, preds)]d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])predict(net, test_iter)
结果如下:
模型的保存与获取
torch.save(net,'这里填保存地址')
modlue = torch.load('这里填模型地址')
相关文章:

多层感知机
多层感知机理论部分 本文系统的讲解多层感知机的pytorch复现,以及详细的代码解释。 部分文字和代码来自《动手学深度学习》!! 目录多层感知机理论部分隐藏层多层感知机数学逻辑激活函数1. ReLU函数2. sigmoid函数3. tanh函数多层感知机的从零…...

python在windows调用svn-pysvn
作为EBS开发人员,开发工具用的多,部署代码类型多,管理程序麻烦,操作繁琐,一直是我最讨厌的事情。部署一次程序要使用好几个工具,改来改去,上传下载,实在难受。 扣了一下python&#…...
office365 word 另存为 pdf 的注意事项和典型设置
0. 操作环境介绍 Office 版本:Office 365 版本 不同版本的操作可能有所不同 1. 基本操作 – 另存为 pdf 【文件】 --> 【另存为】,选择适当的文件路径、文件名保存类型选择【PDF】点击【保存】 1. 导出的pdf包含目录标签 word中,可使用…...
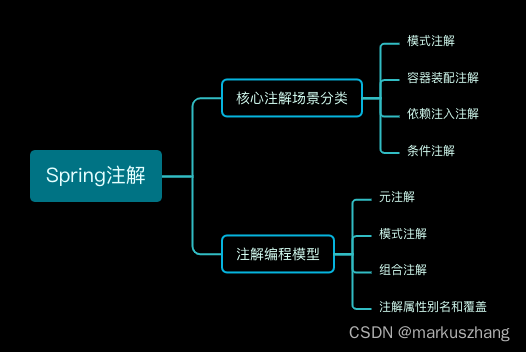
Spring IoC容器之常见常用注解以及注解编程模型简介
一、全文概览 本篇文章主要学习记录Spring中的核心注解,罗列常见常用的注解以及Spring中的注解编程模型介绍 二、核心注解 1、Spring模式注解 常用注解场景描述Spring起始支持版本Component通用组件模式注解,是所有组件类型注解的元注解Spring 2.5Repo…...
超详细讲解文件函数
超详细讲解文件函数!!!!字符输入/输出函数fgetcfputc文本行输入/输出函数fgetsfputs格式化输入/输出函数fscanffprintf二进制输入/输出函数freadfwrite打开/关闭文件函数fopenfclose字符输入/输出函数 fgetc fgetc函数可以从指定…...

【挣值分析】
名称解释 拼写解释PV计划费用,预估预算EV挣值,实际预估预算AC实际费用,实际花费CV成本偏差 (EV - AC)SV进度偏差(EV - PV)CPI成本绩效指数 (EV / AC)SPI进度绩效指数 &a…...

Python3-基础语法
Python3 基础语法 编码 默认情况下,Python 3 源码文件以 UTF-8 编码,所有字符串都是 unicode 字符串。 当然你也可以为源码文件指定不同的编码: # -*- coding: cp-1252 -*-上述定义允许在源文件中使用 Windows-1252 字符集中的字符编码&…...
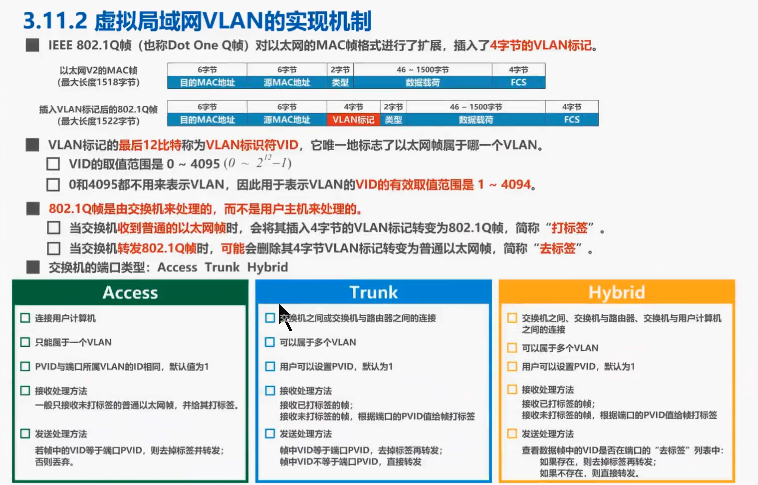
【计算机网络】数据链路层(下)
文章目录媒体接入控制媒体接入控制-静态划分信道随机接入 CSMACD协议随机接入 CSMACA协议MAC地址MAC地址作用MAC地址格式MAC地址种类MAC地址的发送顺序单播MAC地址广播MAC地址多播MAC地址随机MAC地址IP地址区分网络编号IP地址与MAC地址的封装位置转发过程中IP地址与MAC地址的变…...

系统分析师考试大纲
系统分析师考试大纲 1.考试目标 通过本考试的合格人员应熟悉应用领域的业务,能分析用户的需求和约束条件,写出信息系统需求规格说明书,制订项目开发计划,协调信息系统开发与运行所涉及的各类人员;能指导制…...

2023上半年软考报名时间已定,你准备好了吗?
港城软考公众号于2023年2月17日发布了2023年度计算机软考工作计划,从该计划内容得知,2023年计算机软考上半年报名3月13日开始,请相关报考人员提前做好报名准备工作。 其他各省市还暂未公布2023上半年软考报名时间,每年都有很多…...
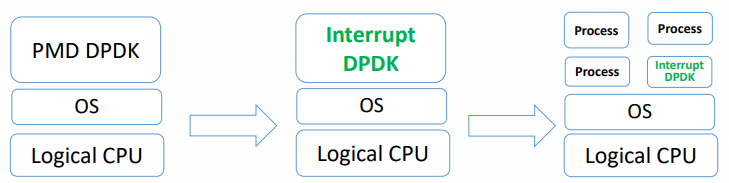
DPDK — Userspace PMD 源码分析
目录 文章目录目录PMD driver 通过 IGB_UIO 与 UIO 进行交互注册一个 UIO 设备PMD 的应用层实现PMD 同样支持中断处理方式PMD driver 通过 IGB_UIO 与 UIO 进行交互 IGB_UIO 内核模块的另一个主要功能就是让用于态的 PMD 网卡驱动程序得以与 UIO 进行交互。对于 PMD 的实现来说…...
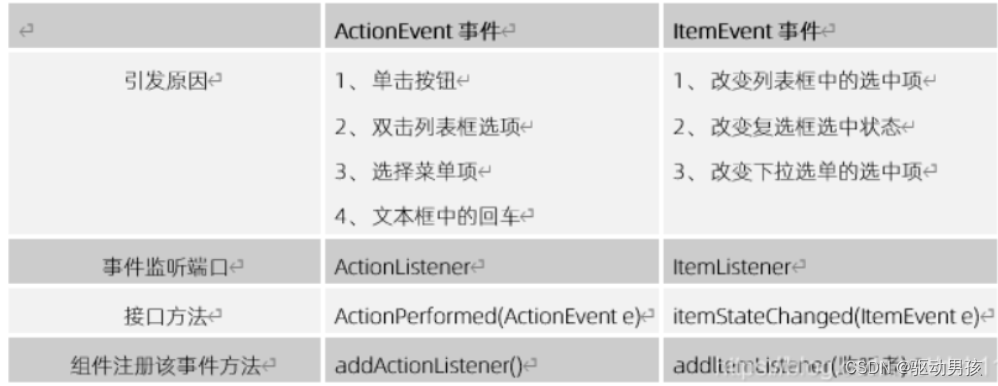
javase基础学习(终)
9、网络通信协议 /* InetAddress类的常用方法 1、getLocalHost()public static InetAddress getLocalHost() throws UnknownHostException返回本地主机的地址。 这是通过从系统检索主机的名称,然后将该名称解析为InetAddress 。2、getByName()public static InetAd…...

Scala
1、Scala语言有什么特点?什么是函数式编程?有什么优点? 1、scala语⾔集成⾯向对象和函数式编程 2、函数式编程是⼀种典范,将电脑的运算视作是函数的运算 3、与过程化编程相⽐,函数式编程⾥的函数计算可以随时调⽤&…...

《数据分析方法论和业务实战》读书笔记
《数据分析方法和业务实战》读书笔记 共9章:前两章入门,3-7章介绍基本方法,8章从项目实战介绍数据分析,9章答疑常见问题。 1 数据分析基础 数据分析的完整流程 数据-》信息-〉了解现状-》发现原因-〉获取洞察-》问题机会-〉驱动…...
)
华为OD机试 - 射击比赛(Python)
射击比赛 题目 给定一个射击比赛成绩单 包含多个选手若干次射击的成绩分数 请对每个选手按其最高三个分数之和进行降序排名 输出降序排名后的选手 ID 序列 条件如下: 一个选手可以有多个射击成绩的分数 且次序不固定如果一个选手成绩小于三个 则认为选手的所有成绩无效 排名忽…...

uniapp自定义验证码输入框,隐藏光标
一. 前言 先看下使用场景效果图: 点击输入框唤起键盘,蓝框就相当于input的光标,验证码输入错误或者不符合格式要求会将字体以及边框改成红色提示,持续1s,然后清空数据,恢复原边框样式;5位验证…...
基于SSM框架的生活论坛系统的设计与实现
基于SSM框架的生活论坛系统的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景…...

spring注解使用中常见的概念性问题
Spring注解使用中常见的概念性问题Configuration有什么用?Configuration和XML有什么区别?哪种好?Autowired 、 Inject、Resource 之间有什么区别?Value、PropertySource 和 Configuration?Spring如何处理带Configurati…...

Module理解及使用
ES6的模块化设计思想是静态化,也就是说,在编译的时候确定模块的依赖关系,以及输出输出入的变量。而CommonJS和AMD模块都是在运行时确定的。ES6的模块不是对象,而是通过export显示指定输出的代码,再通过import命令输入。…...

ngix 常用配置之 location 匹配规则
大家好,我是 17。 今天和大家详细聊聊 nginx 的 location 匹配规则 location 匹配规则 匹配规则在后面的 try_files 中有举例 location 按如下优先级匹配 绝对匹配,一个字符也不能差^~ 前缀匹配~(区分大小写), ~*(不…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
