2023年国赛数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录
- 算法介绍
- FP树表示法
- 构建FP树
- 实现代码
- 建模资料
## 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
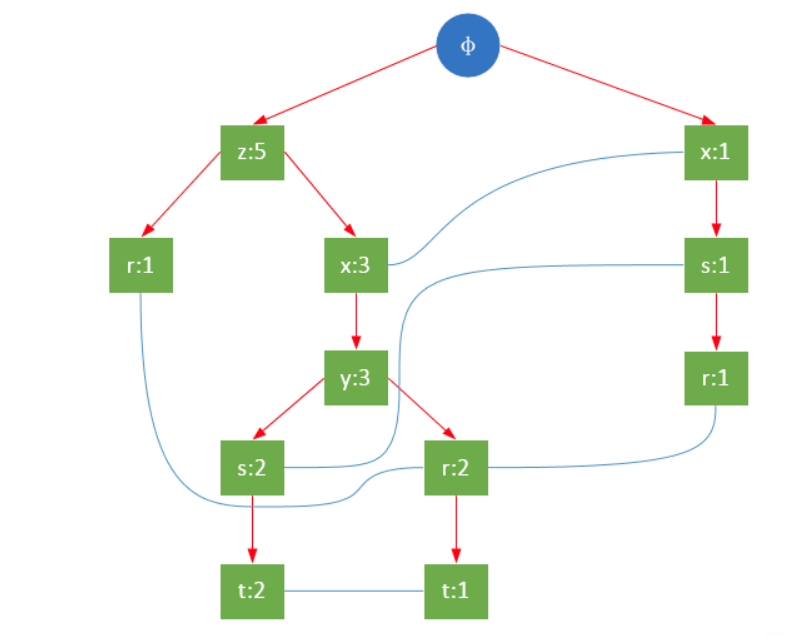
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
构建FP树
现在有如下数据:
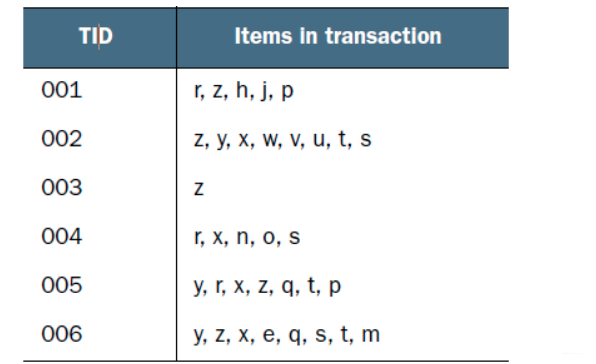
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
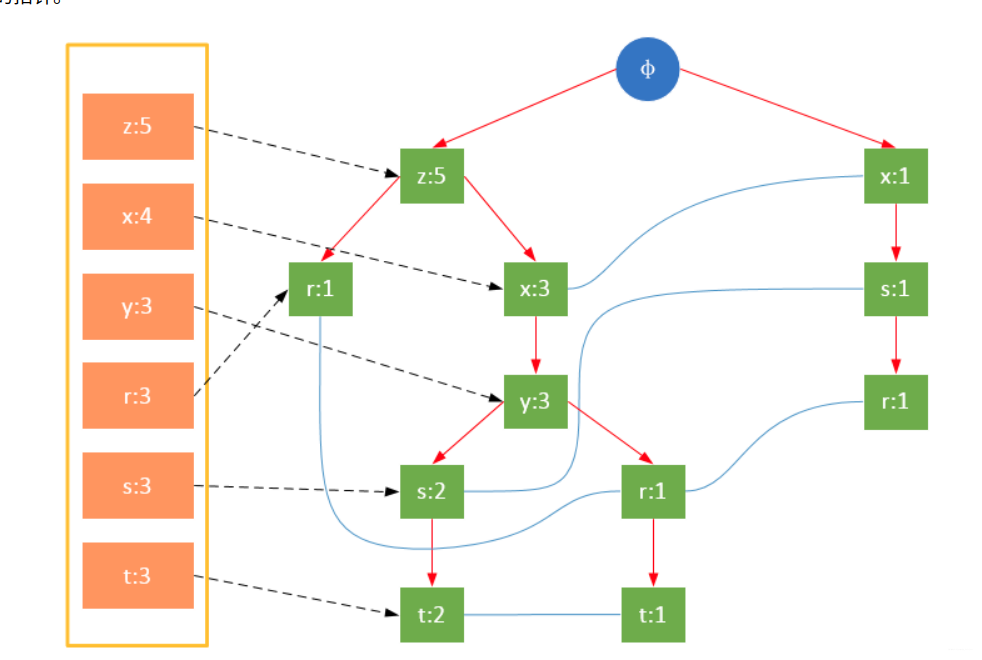
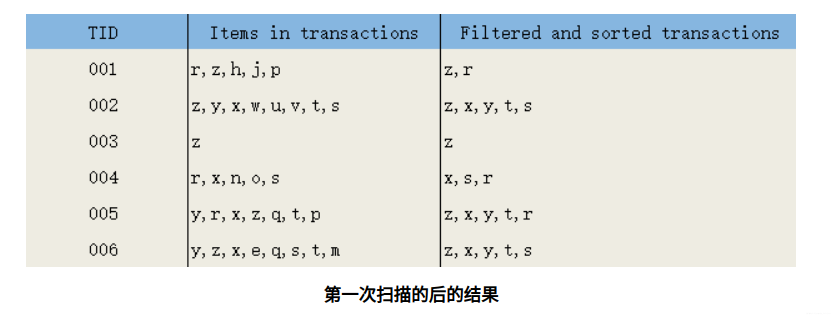
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
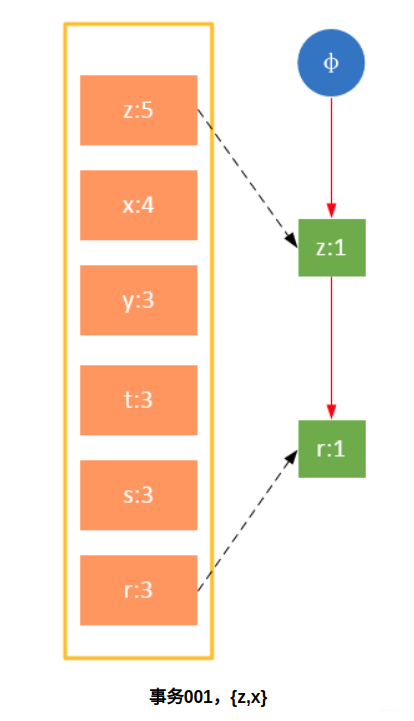
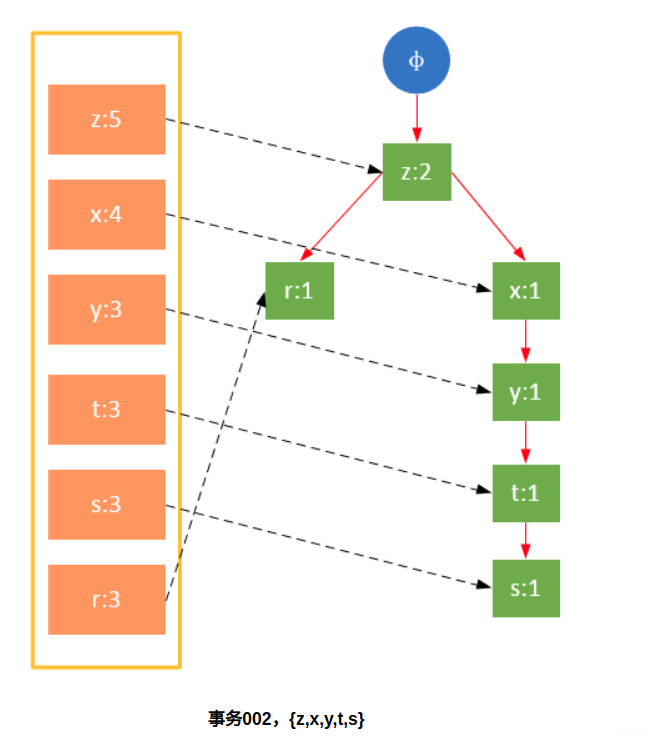
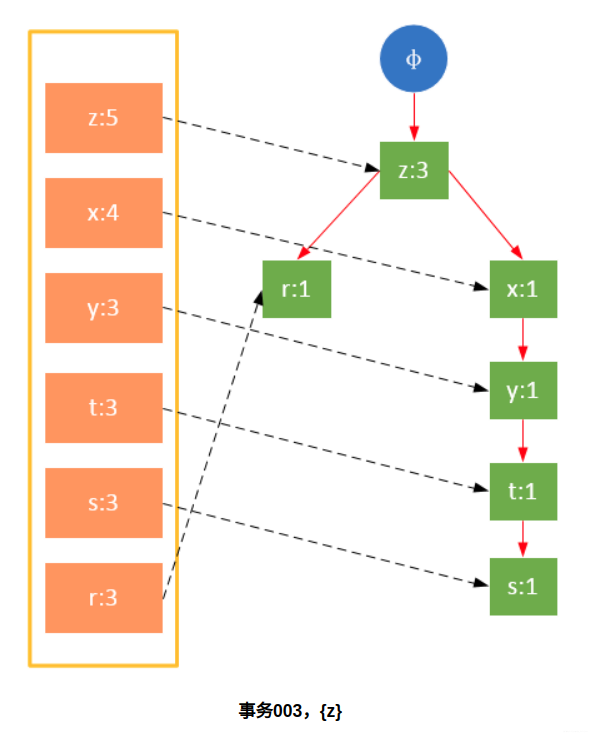
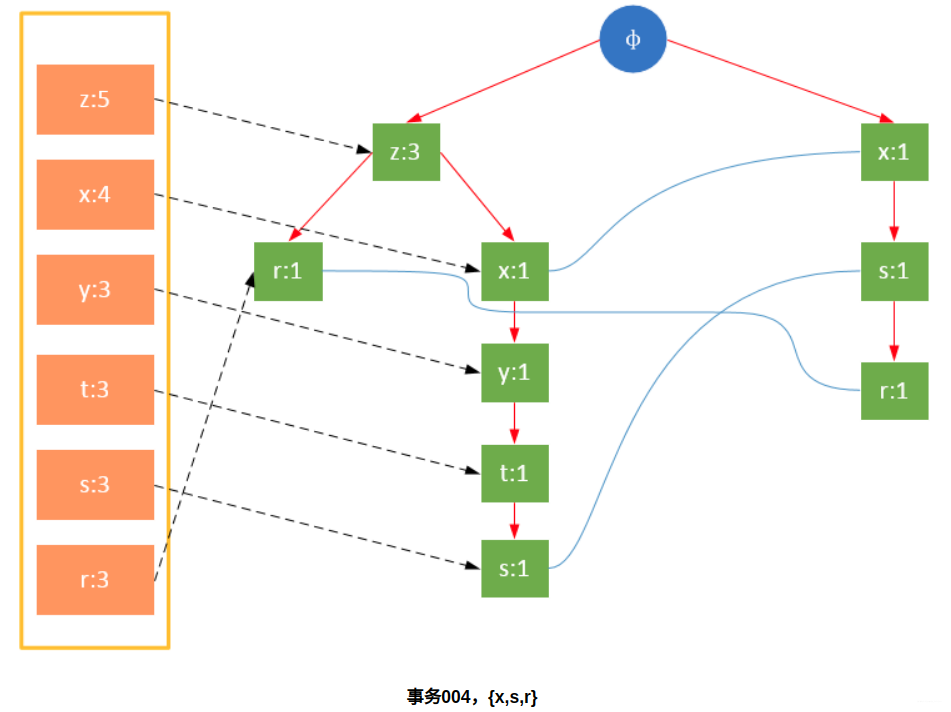
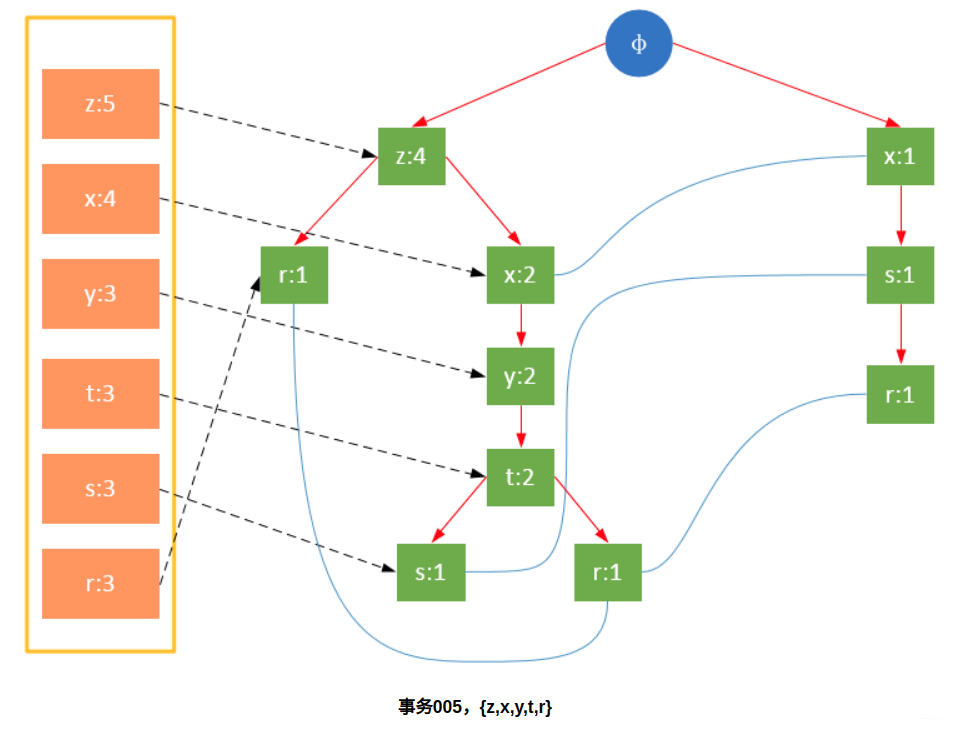
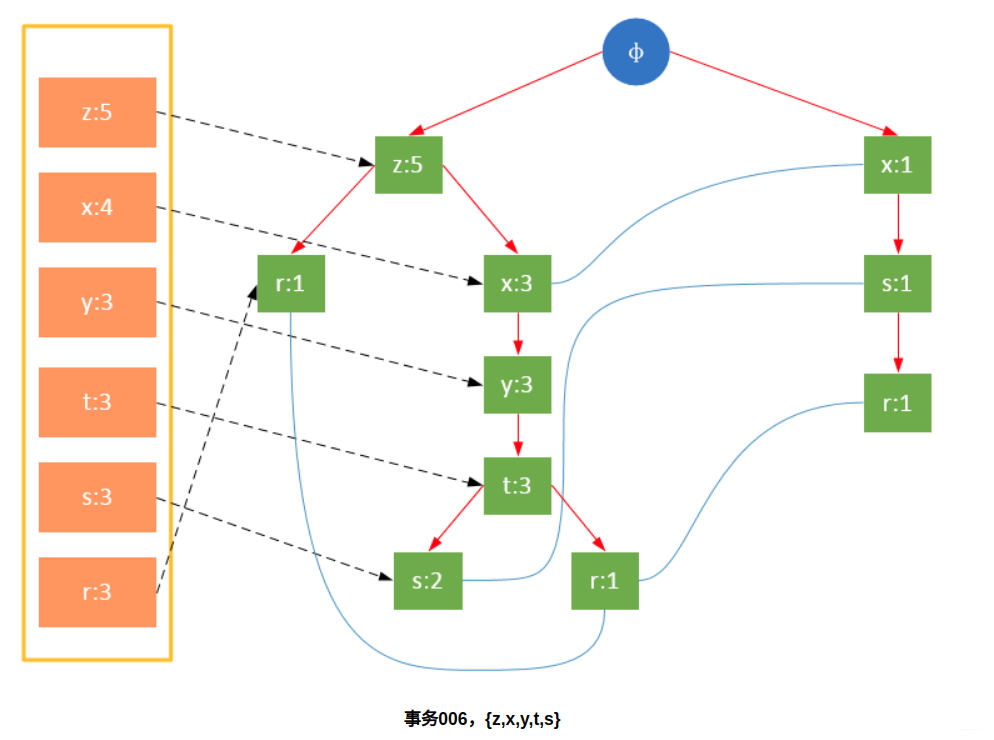
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023年国赛数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录 算法介绍FP树表示法构建FP树实现代码 建模资料 ## 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,…...

Positive Technologies:有针对性的攻击占非洲所有攻击的 68%
网络犯罪分子最常攻击的是非洲的金融公司和电信公司 Positive Technologies 分析了 2022–2023 年非洲遇到的各种网络安全威胁,并在圣彼得堡举行的第二届俄罗斯—非洲峰会上介绍了研究结果。根据我们的专家的介绍,非洲金融部门受到的网络攻击最多&#…...
Flink CDC系列之:TiDB CDC 导入 Elasticsearch
Flink CDC系列之:TiDB CDC 导入 Elasticsearch 一、通过docker 来启动 TiDB 集群二、下载 Flink 和所需要的依赖包三、在TiDB数据库中创建表和准备数据四、启动Flink 集群,再启动 SQL CLI五、在 Flink SQL CLI 中使用 Flink DDL 创建表六、Kibana查看Ela…...

未来混合动力汽车的发展:技术探索与前景展望
随着环境保护意识的增强和对能源消耗的关注,混合动力汽车成为了汽车行业的研发热点。混合动力汽车融合了传统燃油动力和电力动力系统,通过优化能源利用效率,既降低了燃油消耗和排放,又提供了更长的续航里程。本文将探讨混合动力汽…...

C进阶(2/7)前篇——指针进阶
前言:本文章讲解部分指针进阶内容。后续继续更新。 文章重点: 1. 字符指针 2. 数组指针 3. 指针数组 4. 数组传参和指针传参 目录 前言:本文章讲解部分指针进阶内容。后续继续更新。 指针初阶了解: 1.字符指针 1.1一道有关于字…...
C 内存分配器 mimalloc
有论文 … … https://www.microsoft.com/en-us/research/publication/mimalloc-free-list-sharding-in-action/ 可以减少内存碎片,微软研究院2019 年开源出的内存分配器 代码,适配linux...

leetcode做题笔记74搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。 思…...

深信服数据中心管理系统 XXE漏洞复现
0x01 产品简介 深信服数据中心管理系统DC为AC的外置数据中心,主要用于海量日志数据的异地扩展备份管理,多条件组合的高效查询,统计和趋势报表生成,设备运行状态监控等功能。 0x02 漏洞概述 深信服数据中心管理系统DC存在XML外部实…...

【Kubernetes】Kubernetes的Pod进阶
Pod进阶 一、资源限制和重启策略1. 资源限制2. 资源单位2.1 CPU 资源单位2.2 内存 资源单位 3. 重启策略(restartPolicy) 二、健康检查的概念1. 健康检查1.1 探针的三种规则1.2 Probe 支持三种检查方法 2. 示例2.1 exec 方式2.2 httpGet 方式2.3 tcpSock…...

都错了!机械硬盘远比SSD更省电 最多领先94%
相信在绝大多数人的认知中,SSD固态硬盘因为没有HDD机械硬盘那样的移动部件,不但更稳定,还更省电。 但是,存储服务商Scality的研究表明,恰恰相反,HDD更省电。 他们以美光6500 ION 30.72TB QLC SSD、希捷银河…...
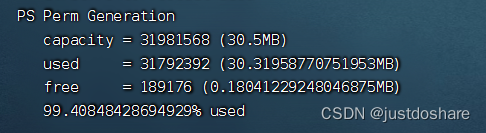
tomcat设置PermSize
最近tomcat老是报错,查看了日志出现PermGen 内存不够用,重启tomcat后查询使用情况 通过启动参数发现没有设置 PermGen,继续通过jmap查看 jmap -heap 21179 发现99%已使用,而且默认是30.5M,太小了,这里设置成256M 1. 创建setenv.sh文件 在/usr/local/tomcat/bin目录下创建一个…...
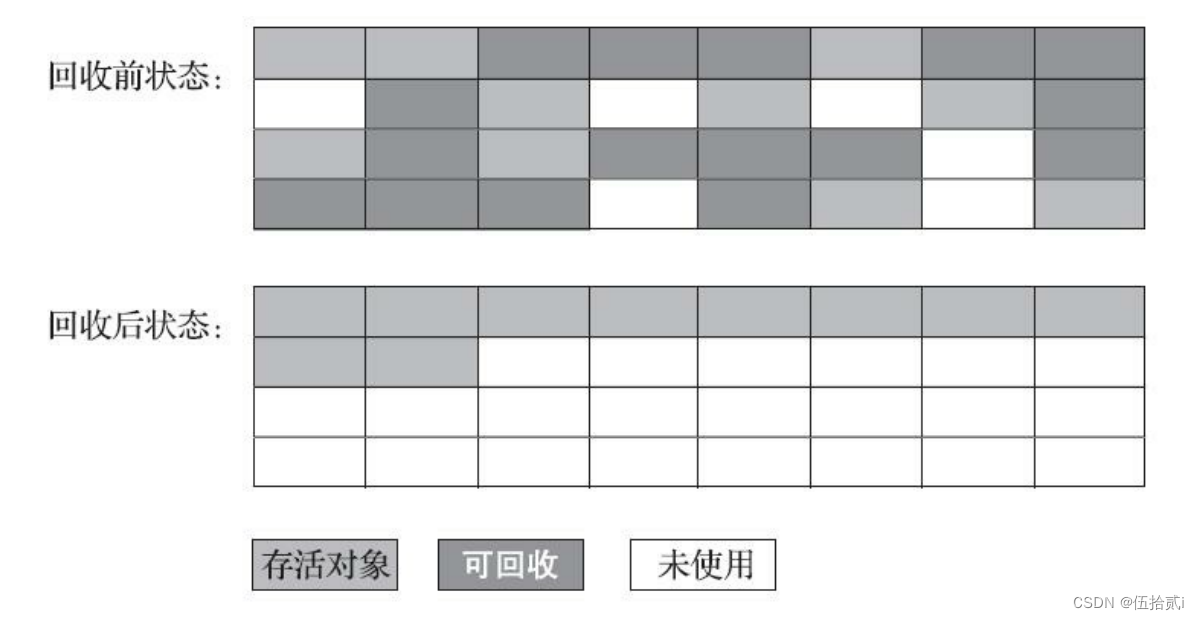
JVM——分代收集理论和垃圾回收算法
一、分代收集理论 1、三个假说 弱分代假说:绝大多数对象都是朝生夕灭的。 强分代假说:熬过越多次垃圾收集过程的对象越难以消亡。 这两个分代假说共同奠定了多款常用的垃圾收集器的一致的设计原则:收集器应该将Java堆划分出不同的区域&…...

jar包独立运行的几种方式
linux启动jar包的方式,直接运行与守护进程运行 通常我们开发好的程序需要打成war/jar包,在linux运行,war包好说直接丢在tomcat中即可,如果开发好的程序为jar包的话,方式比较多 直接启动(java-jar xxx.jar) java -jar shareniu.jar 特点:当前ssh窗口被锁定&#x…...

[python] 安装numpy+scipy+matlotlib+scikit-learn及问题解决
这篇文章主要讲述Python如何安装Numpy、Scipy、Matlotlib、Scikit-learn等库的过程及遇到的问题解决方法。最近安装这个真是一把泪啊,各种不兼容问题和报错,希望文章对你有所帮助吧!你可能遇到的问题包括: ImportError: N…...

uniapp使用命令创建页面
package.js下创建命令 "scripts": {"add": "node ./auto/addPage.ts" } package.js同级目录创建auto/addPage.ts addPage.ts代码如下 const fs require(fs) const path require(path) const targetPath process.argv[2];// 要创建的目录地…...

Linux(进程控制)
进程控制 进程创建fork函数初识fork函数返回值写时拷贝fork常规用法fork调用失败的原因 进程终止进程退出码进程常见退出方法 进程等待进程等待必要性获取子进程status进程等待的方法 阻塞等待与非阻塞等待阻塞等待非阻塞等待 进程替换替换原理替换函数函数解释命名理解 做一个…...
进制介绍)
Java学习笔记——(18)进制介绍
对于整数,有四种表示方式: 二进制:0,1 ,满 2 进 1.以 0b 或 0B 开头。(注:书写二进制时需要按四位数字一组的方式书写,缺的前面补0)十进制:0-9 ,满 10 进 1。…...
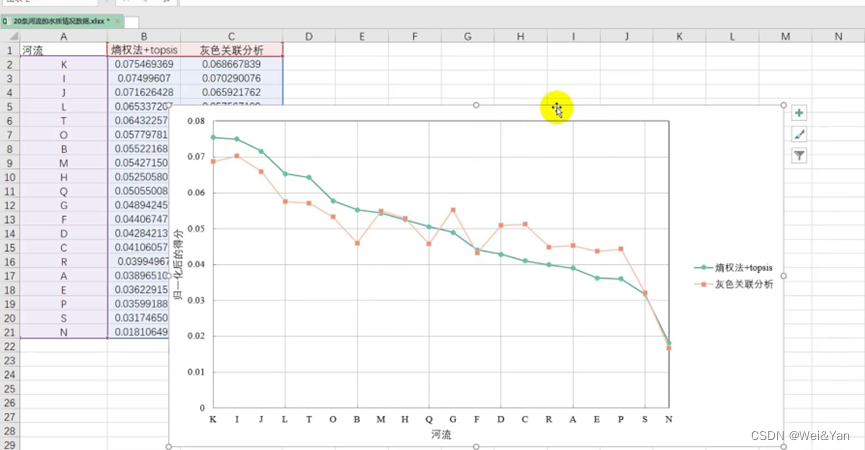
【数学建模】--灰色关联分析
系统分析: 一般的抽象系统,如社会系统,经济系统,农业系统,生态系统,教育系统等都包含有许多种因素,多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中,哪些是主要…...

图像像素梯度
梯度 在高数中,梯度是一个向量,是有方向有大小。假设一二元函数f(x,y),在某点的梯度有: 结果为: 即方向导数。梯度的方向是函数变化最快的方向,沿着梯度的方向容易找到最大值。 图像梯度 在一幅模糊图…...

[论文笔记]Batch Normalization
引言 本文是论文神作Batch Normalization的阅读笔记,这篇论文引用量现在快50K了。 由于上一层参数的变化,导致每层输入的分布会在训练期间发生变化,让训练深层神经网络很复杂。这会拖慢训练速度,因为需要更低的学习率并小心地进行参数初始化,使得很难训练这种具有非线性…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
