代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列
392.判断子序列
392.判断子序列
思路:
(这道题也可以用双指针的思路来实现,时间复杂度也是O(n))
这道题应该算是编辑距离的入门题目,因为从题意中我们也可以发现,只需要计算删除的情况,不用考虑增加和替换的情况。
所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。
动态规划五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
- 确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
- if (s[i - 1] == t[j - 1])
t中找到了一个字符在s中也出现了 - if (s[i - 1] != t[j - 1])
相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
- dp数组如何初始化
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
dp[i][0] 表示以下标i-1为结尾的字符串,与空字符串的相同子序列长度,所以为0. dp[0][j]同理。
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
- 确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右

- 举例推导dp数组
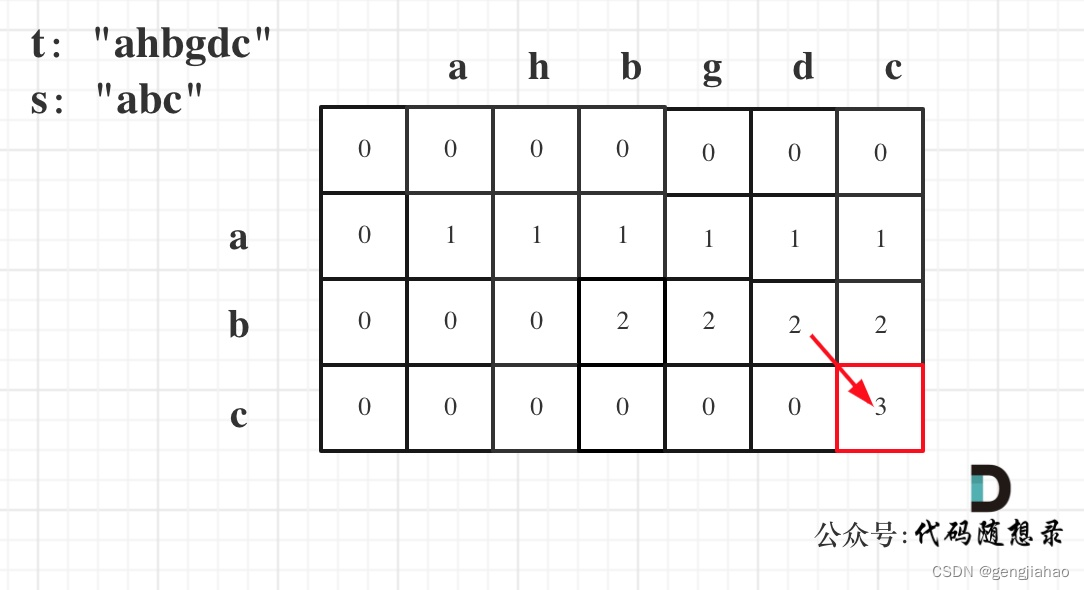
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
代码:
python
class Solution(object):def isSubsequence(self, s, t):""":type s: str:type t: str:rtype: bool"""dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = dp[i][j-1]return dp[-1][-1] == len(s)
115.不同的子序列
115.不同的子序列
思路:
动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
- 确定递推公式
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
这里可能有录友不明白了,为什么还要考虑 不用s[i - 1]来匹配,都相同了指定要匹配啊。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
- dp数组如何初始化
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。

每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起,但我为了凸显初始化的逻辑,所以还是加上了。
- 确定遍历顺序
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
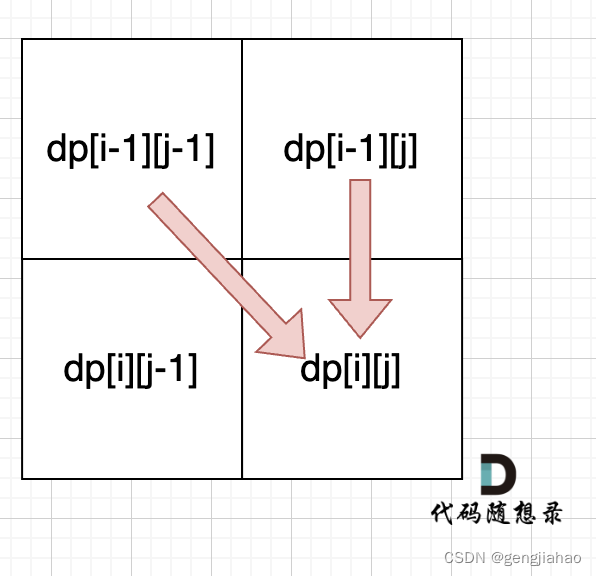
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}
}
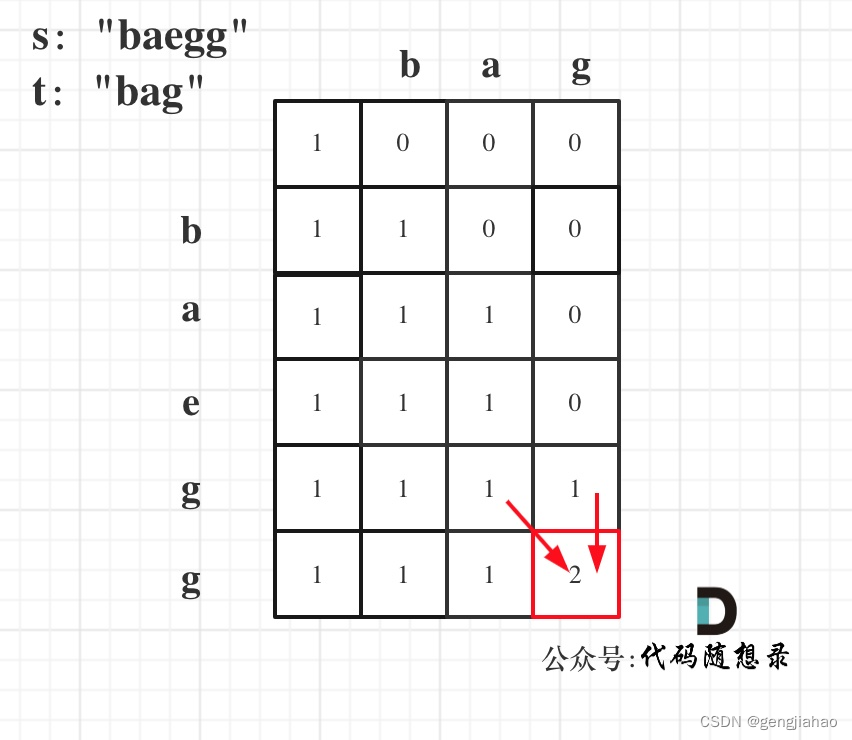
- 举例推导dp数组
以s:“baegg”,t:"bag"为例,推导dp数组状态如下:
代码:
python
class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(len(s)):dp[i][0] = 1for j in range(1, len(t)):dp[0][j] = 0for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]else:dp[i][j] = dp[i-1][j]return dp[-1][-1]
相关文章:

代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列 392.判断子序列 392.判断子序列 思路: (这道题也可以用双指针的思路来实现,时间复杂度也是O(n)) 这道题应该算是编辑距…...

日常BUG——普通页面跳转tabbar页面报错
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 微信小程序页面跳转的时候出现下面的问题: wx.redirectTo({url: /pages/index/i…...
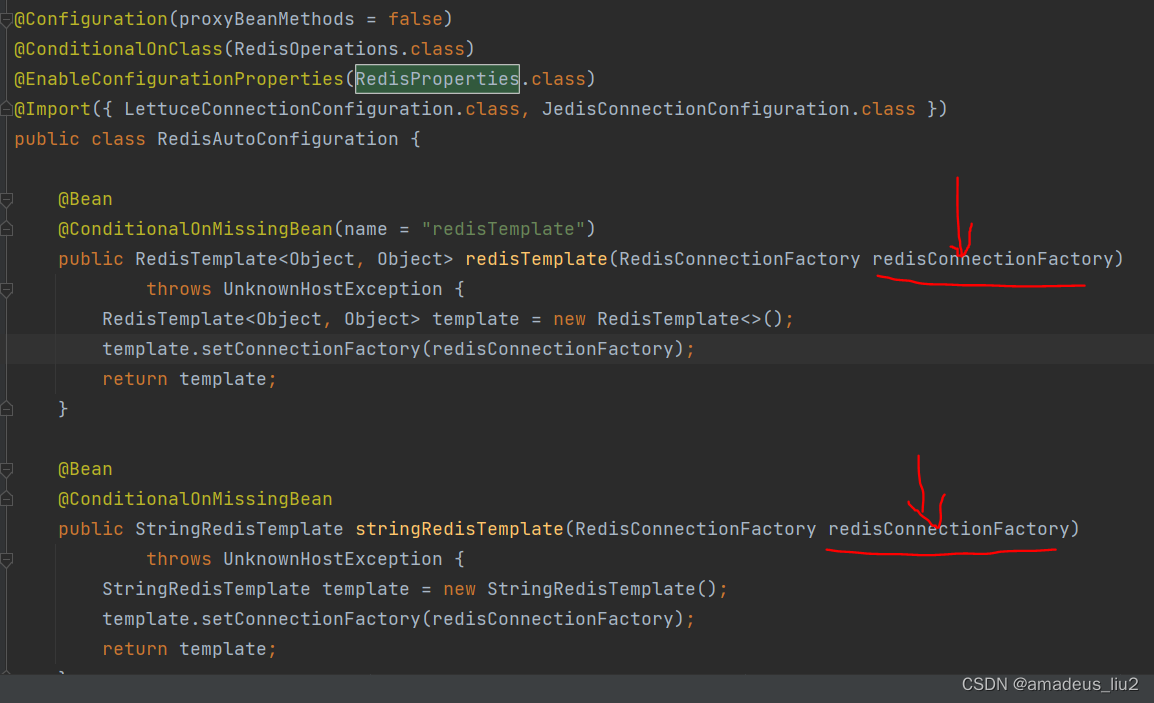
SpringBoot复习:(48)RedisAutoConfiguration自动配置类
RedisAutoConfiguration类代码如下: 可以看到在这个类中配置了2个bean: redisTemplate和stringRedisTemplate. 而它通过EnableConfigurationProperties(RedisProperties.class)注解,把配置文件中配置的Redis相关的信息引入进来了,RedisPrope…...

软硬件免费,服务收费:网络安全商业模式正在被颠覆
大数据产业创新服务媒体 ——聚焦数据 改变商业 从元宇宙到造汽车,重回国内A股市场五年的360一路苦追热点。一直到大模型横空出世,360才算真正找到感觉,经历一次战略上的回归。 在8月9日的互联网安全大会上,一袭红衣的红衣教主周…...
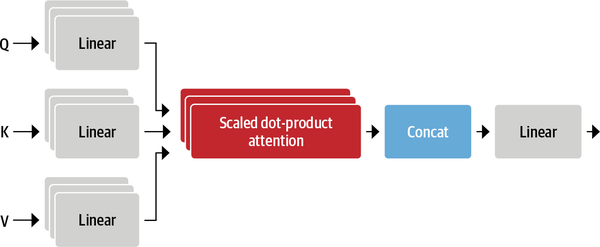
变形金刚:从零开始【01/2】
一、说明 在我们的日常生活中,无论你是否是数据科学家,你都在单向地使用变压器模型。例如。如果您使用的是 ChatGPT 或 GPT-4 或任何 GPT,那么在为您回答问题的框中是变压器的一部分。如果您是数据科学家或数据分析师,则可能正在使…...
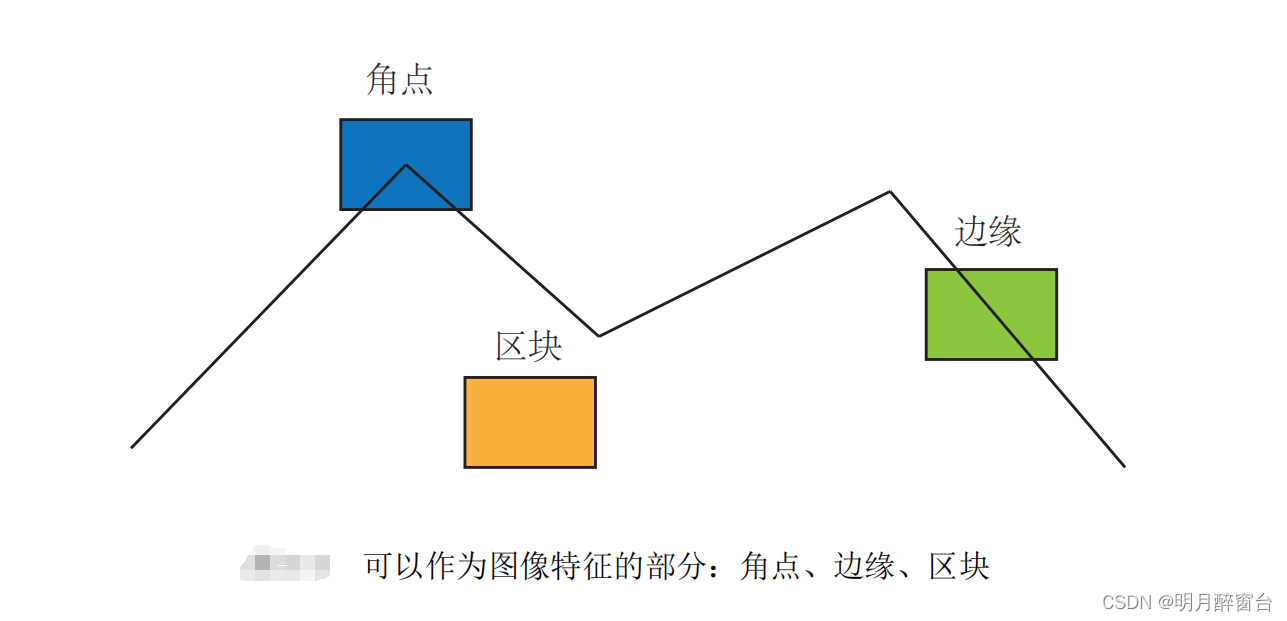
Opencv特征检测之ORB算法原理及应用详解
Opencv特征检测之ORB算法原理及应用详解 特征是图像信息的另一种数字表达形式。一组好的特征对于在指定 任务上的最终表现至关重要。视觉里程 (VO) 的主要问题是如何根据图像特征来估计相机运动。但是,整幅图像用来计算分析通常比较耗时,故而转换为分析图像中的特征点的运动…...

【es6】函数柯里化(Currying)
柯里化(Currying):把接受多个参数的函数变换成接受一个单一参数(最初函数的第一个参数)的函数,并且返回接受余下的参数且返回结果的新函数。 柯里化由 Christopher Strachey 以逻辑学家 Haskell Curry 命名的,它是 Mos…...

线上多域名实战
本文博主给大家分享线上多域名实战,当线上主域名不可用的情况下,启用备用域名完成网站高可用保障。 网站的高可用性一直是网站运维的重中之重。一旦网站宕机,不仅会造成巨大的经济损失,也会严重影响用户体验。备份域名就是一种实现…...

【C语言】上手实验
实验1 顺序、分支结构 程序填空 1. 题目描述:输入三个整数存放在变量a、b、c中,找出三个数中的最大值放于max中,并将其输出。以下是完成此项工作的程序,请将未完成的部分填入,实现其功能,并在计算机上…...

设计HTML5表单
HTML5基于Web Forms 2.0标准对HTML4表单进行全面升级,在保持简便、易用的基础上,新增了很多控件和属性,从而减轻了开发人员的负担。表单为访问者提供了与网站进行互动的途径,完整的表单一般由控件和脚本两部分组成。 1、认识HTML…...
使用Kaptcha生成验证码
说明:验证码,是登录流程中必不可少的一环,一般企业级的系统,使用都是专门制作验证码、审核校验的第三方SDK(如极验)。本文介绍,使用谷歌提供的Kaptcha技术,制作一个简单的验证码。 …...
【vue】vue中的插槽以及使用方法
插槽 普通插槽 1、在父组件中直接调用子组件的标签,是可以渲染出子组件的内容;如果在子组件标签中添加了内容,父组件就渲染不出来了; ParentComponent.vue: <template><div><h1>Parent Componen…...
javaScript:分支语句的理解与使用(附带案例)
目录 前言 补充 另一种说法 分支语句 1.if语句 a.单分支语句 注意 b.双分支语句 注意点 c.多分支语句(分支语句的联级语句) 补充 2.三元运算符 三元运算符 ? : 使用场景 3.switch语句 解释 释义:…...
事务的并发问题和隔离级别)
MySQL高阶知识点(一)事务的并发问题和隔离级别
简单来说,事务就是要保证一组数据库操作,要么全部成功,要么全部失败。 在 MySQL 中,事务支持是在引擎层实现的。 MySQL 是一个支持多引擎的系统,但并不是所有的引擎都支持事务。 如 MySQL 原生的 MyISAM 引擎就不支持…...
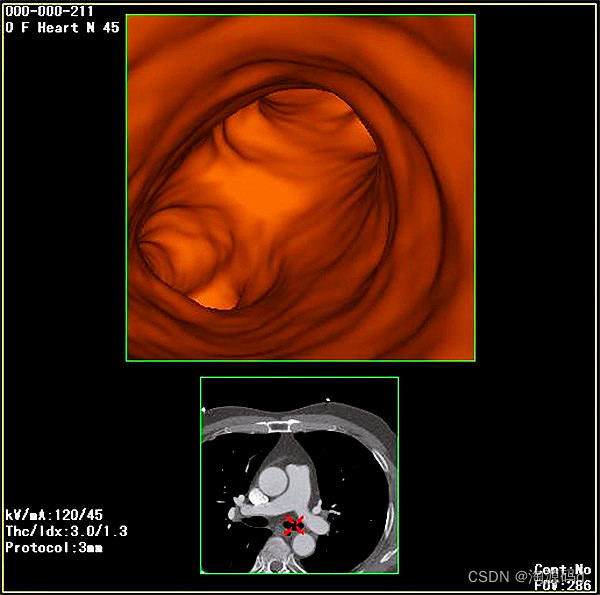
医疗PACS源码,支持三维多平面重建、三维容积重建、三维表面重建、三维虚拟内窥镜
C/S架构的PACS系统源码,PACS主要进行病人信息和影像的获取、处理、存储、调阅、检索、管理,并通过网络向全院提供病人检查影像及诊断报告;各影像科室之间共享不同设备的病人检查影像及诊断报告;在诊断工作站上,调阅HIS中病人的其它…...
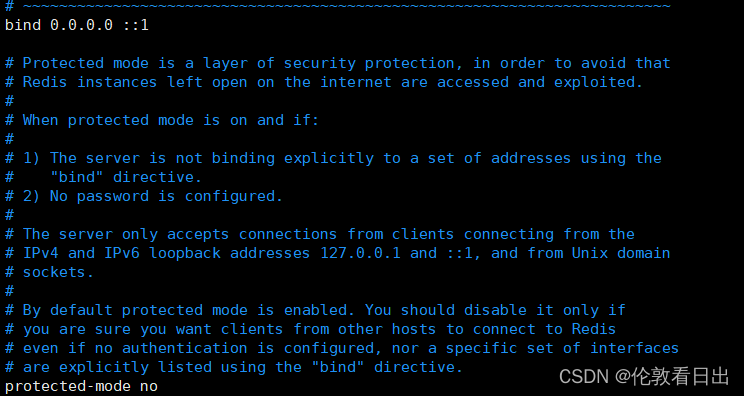
Ubuntu安装Redis
首先要切换到root用户 1.apt安装 apt install redis 2.⽀持远程连接 修改 /etc/redis/redis.conf • 修改 bind 127.0.0.1 为 bind 0.0.0.0 • 修改 protected-mode yes 为 protected-mode no 3.控制 Redis 启动 1.启动 Redis 服务 service redis-server start 2.停⽌ Redis …...

“深入解析JVM内部机制:探索Java虚拟机的奥秘“
标题:深入解析JVM内部机制:探索Java虚拟机的奥秘 JVM(Java虚拟机)是Java程序的核心执行环境,它负责将Java字节码转换为机器码并执行。了解JVM的内部机制对于理解Java程序的执行过程和性能优化至关重要。本文将深入解析…...

vim打开文件中文是乱码
vim打开文件中文是乱码 问题:在Linux系统下,使用cat查看含有中文的文本文件正常,但是使用vim打开却是乱码 解决方法: 方法一: 在文件中设定 在vim的退出模式下 :set encodingutf8 方法二: 直接写入/etc/…...

【正点原子STM32连载】 第七章 Geehy标准库版本MDK工程创建 摘自【正点原子】APM32F407最小系统板使用指南
1)实验平台:正点原子stm32f103战舰开发板V4 2)平台购买地址:https://detail.tmall.com/item.htm?id609294757420 3)全套实验源码手册视频下载地址: http://www.openedv.com/thread-340252-1-1.html# 第七…...
的不同用法)
SQL中count()的不同用法
1.count(*):统计所有列的行数,包括均为null值的行; 2.count(1):统计所有列的行数,包括均为null值的行; 3.count(列名):统计指定列的行数,不包括null值; 实例:…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
