OpenCV-Python中的图像处理-霍夫变换
OpenCV-Python中的图像处理-霍夫变换
- 霍夫变换
- 霍夫直线变换
- 霍夫圆环变换
霍夫变换
- 霍夫(Hough)变换在检测各种形状的技术中非常流行,如果要检测的形状可以用数学表达式描述,就可以是使用霍夫变换检测它。即使要检测的形状存在一点破坏或者扭曲也是可以使用。
霍夫直线变换
- Hough直线变换,可以检测一张图像中的直线
- cv2.HoughLines(image, rho, theta, threshold)
- return:返回值就是( ρ, θ)。 ρ 的单位是像素, θ 的单位是弧度。
- image:是一个二值化图像,所以在进行霍夫变换之前要首先进行二值化,或者进行Canny 边缘检测。
- rho:代表 ρ 的精确度。
- theta:代表θ 的精确度。
- threshold:阈值,只有累加其中的值高于阈值时才被认为是一条直线,也可以把它看成能检测到的直线的最短长度(以像素点为单位)。
- cv2.HoughLinesP(image: Mat, rho, theta, threshold, lines=…, minLineLength=…, maxLineGap=…)
- return :返回值就是直线的起点和终点(x1,y1,x2,y2)。
- rho:代表 ρ 的精确度。
- theta:代表θ 的精确度。
- threshold:阈值,只有累加其中的值高于阈值时才被认为是一条直线,也可以把它看成能检测到的直线的最短长度(以像素点为单位)。
- minLineLength:直线的最短长度。比这个短的线都会被忽略。
- maxLineGap- 两条线段之间的最大间隔,如果小于此值,这两条直线就被看成是一条直线。
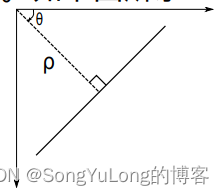
- 一条直线可以用数学表达式 y = mx + c 或者 ρ = x cos θ + y sin θ 表示。ρ 是从原点到直线的垂直距离, θ 是直线的垂线与横轴顺时针方向的夹角(如果使用的坐标系不同,方向也可能不同,这里是按 OpenCV 使用的坐标系描述的)。如下图所示:
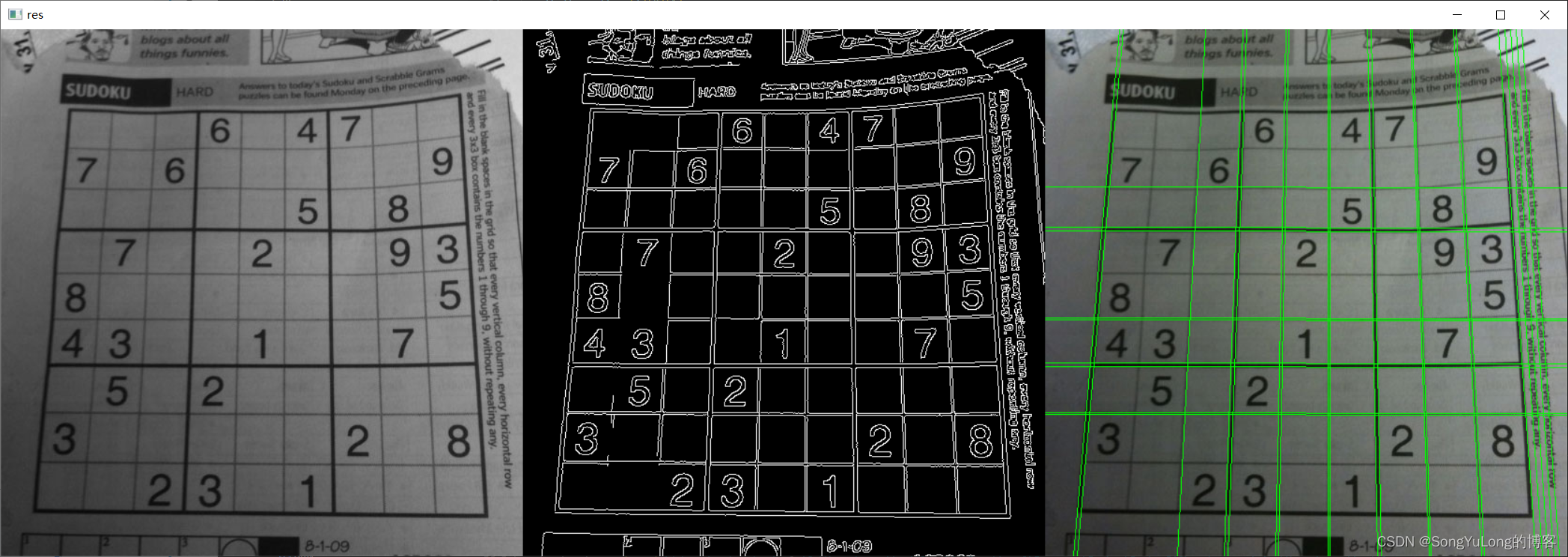
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/sudoku.png', cv2.IMREAD_COLOR)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray, 50, 150, apertureSize=3)lines = cv2.HoughLines(edges, 1, np.pi/180, 200)for i in range(len(lines)):
# for rho, thetha in lines[10]:rho = lines[i][0][0]thetha = lines[i][0][1]a = np.cos(thetha)b = np.sin(thetha)x0 = a*rhoy0 = b*rholine_length = 1000 # 线长x1 = int(x0 + line_length*(-b))y1 = int(y0 + line_length*(a))x2 = int(x0 - line_length*(-b))y2 = int(y0 - line_length*(a))cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 1)# 因为gray和edges都是单通道的,为了可以和原图拼接合并,需要merge成3通道图像数据
gray = cv2.merge((gray, gray, gray))
edges = cv2.merge((edges,edges,edges))# 图像拼接
res = np.hstack((gray,edges,img))cv2.imshow('res', res)
cv2.waitKey(0)
cv2.destroyAllWindows()
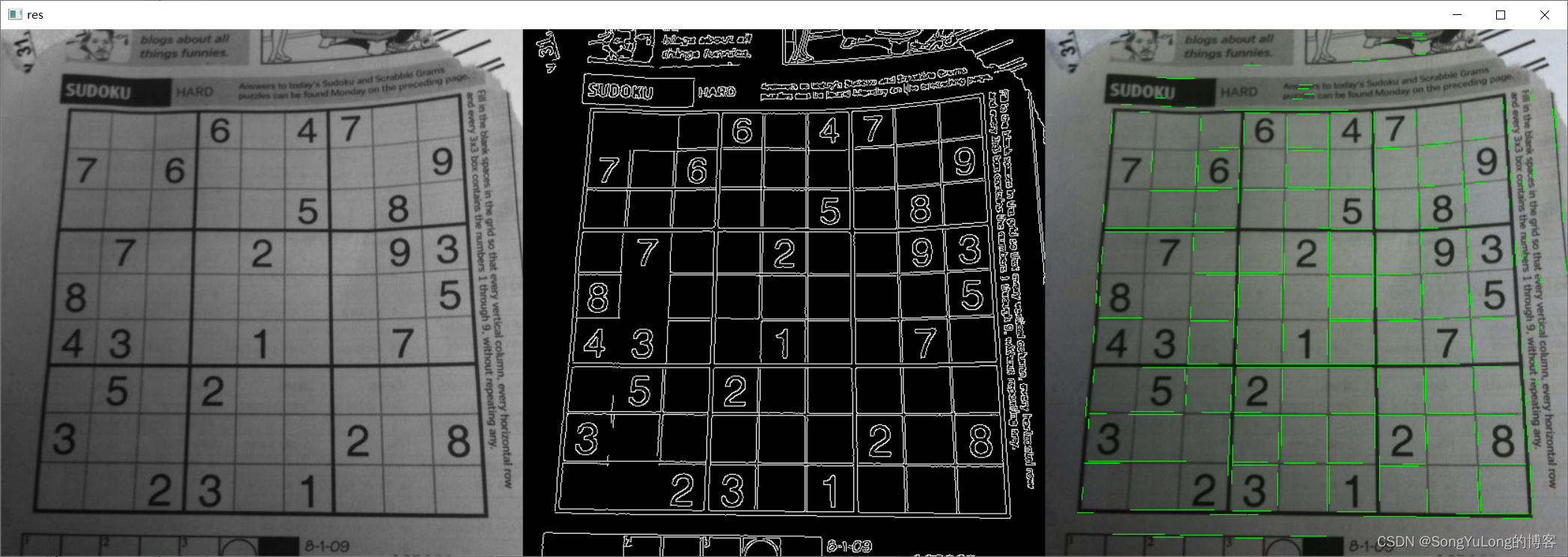
渐进概率式霍夫变换
cv2.HoughLinesP(image: Mat, rho, theta, threshold, lines=…, minLineLength=…, maxLineGap=…)
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/sudoku.png', cv2.IMREAD_COLOR)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 50, 150, apertureSize=3)minLineLength = 100
maxLineGap = 10
# HoughLinesP(image: Mat, rho, theta, threshold, lines=..., minLineLength=..., maxLineGap=...)
lines = cv2.HoughLinesP(canny, 1, np.pi/180, 100, minLineLength, maxLineGap)print(lines.shape)
print(lines[0])for i in range(len(lines)):for x1,y1,x2,y2 in lines[i]:cv2.line(img, (x1, y1), (x2, y2), (0, 255, 0), 1)gray = cv2.merge((gray, gray, gray))
canny = cv2.merge((canny,canny,canny))res = np.hstack((gray, canny, img))
cv2.imshow('res', res)
cv2.waitKey(0)
cv2.destroyAllWindows()
在含有坐标点集合中寻找是否存在直线:
cv2.HoughLinesPointSet(_point, lines_max, threshold, min_rho, max_rho, rho_step, min_theta, max_theta, theta_step, _lines=…)
- _point:输入点的集合,必须是平面内的2D坐标,数据类型必须是CV_32FC2或CV_32SC2。
- lines_max:检测直线的最大数目。
- threshold:累加器的阈值,即参数空间中离散化后每个方格被通过的累计次数大于阈值时则被识别为直线,否则不被识别为直线。
- min_rho:检测直线长度的最小距离,以像素为单位。
- max_rho:检测直线长度的最大距离,以像素为单位。
- rho_step::以像素为单位的距离分辨率,即距离 离散化时的单位长度。
- min_theta:检测直线的最小角度值,以弧度为单位。
- max_theta:检测直线的最大角度值,以弧度为单位。
- theta_step:以弧度为单位的角度分辨率,即夹角 离散化时的单位角度。
- _lines:在输入点集合中可能存在的直线,每一条直线都具有三个参数,分别是权重、直线距离坐标原点的距离 和坐标原点到直线的垂线与x轴的夹角 。
霍夫圆环变换
- 圆形的数学表达式为 (x − xcenter)2+(y − ycenter)2 = r2,其中( xcenter,ycenter)为圆心的坐标, r 为圆的直径。从这个等式中我们可以看出:一个圆环需要 3个参数来确定。所以进行圆环霍夫变换的累加器必须是 3 维的,这样的话效率就会很低。所以 OpenCV 用来一个比较巧妙的办法,霍夫梯度法,它可以使用边界的梯度信息。
- cv2.HoughCircles(image, method, dp, minDist, circles=…, param1=…, param2=…, minRadius=…, maxRadius=…)
- return:存储检测到的圆的输出矢量。
- image:输入图像,数据类型一般用Mat型即可,需要是8位单通道灰度图像
- method:使用的检测方法,cv2.HOUGH_GRADIENT,cv2.HOUGH_GRADIENT_ALT。
- dp:double类型的dp,用来检测圆心的累加器图像的分辨率于输入图像之比的倒数,且此参数允许创建一个比输入图像分辨率低的累加器。上述文字不好理解的话,来看例子吧。例如,如果dp= 1时,累加器和输入图像具有相同的分辨率。如果dp=2,累加器便有输入图像一半那么大的宽度和高度。
- minDist:为霍夫变换检测到的圆的圆心之间的最小距离。
- circles:可以忽略,存储检测到的圆的输出矢量。
- param1:它是第三个参数method设置的检测方法的对应的参数。它表示传递给canny边缘检测算子的高阈值,而低阈值为高阈值的一半。
- param2:也是第三个参数method设置的检测方法的对应的参数,它表示在检测阶段圆心的累加器阈值。它越小的话,就可以检测到更多根本不存在的圆,而它越大的话,能通过检测的圆就更加接近完美的圆形了。
- minRadius:表示圆半径的最小值。
- maxRadius:表示圆半径的最大值。
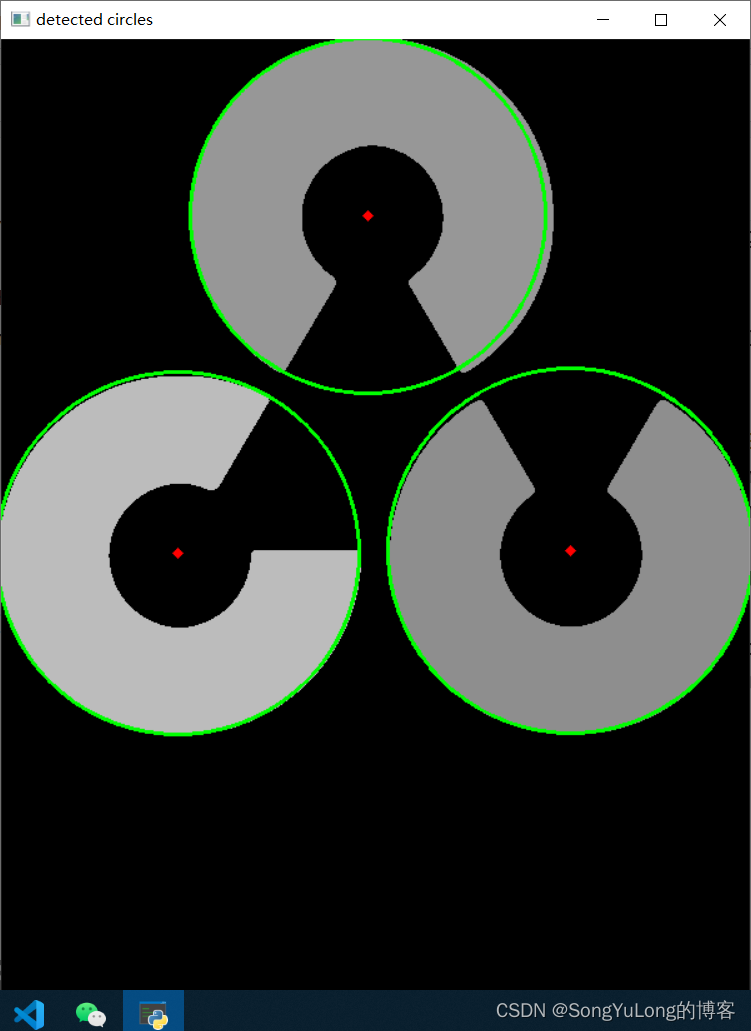
import numpy as np
import cv2img = cv2.imread('./resource/opencv/image/logo/opencv-logo2.png', cv2.IMREAD_GRAYSCALE)
img = cv2.medianBlur(img, 5)
cimg = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)circles = cv2.HoughCircles(img, cv2.HOUGH_GRADIENT, 1, 20, param1=50, param2=30, minRadius=30, maxRadius=0)print(circles)
circles = np.uint16(circles)
print(circles)for i in circles[0, :]:cv2.circle(cimg, (i[0], i[1]), i[2], (0, 255, 0), 2)cv2.circle(cimg, (i[0], i[1]), 2, (0, 0, 255), 3)cv2.imshow('detected circles', cimg)
cv2.waitKey(0)
cv2.destroyAllWindows()
相关文章:

OpenCV-Python中的图像处理-霍夫变换
OpenCV-Python中的图像处理-霍夫变换 霍夫变换霍夫直线变换霍夫圆环变换 霍夫变换 霍夫(Hough)变换在检测各种形状的技术中非常流行,如果要检测的形状可以用数学表达式描述,就可以是使用霍夫变换检测它。即使要检测的形状存在一点破坏或者扭曲也是可以使…...
W5500-EVB-PICO做UDP Client进行数据回环测试(八)
前言 上一章我们用开发板作为UDP Server进行数据回环测试,本章我们让我们的开发板作为UDP Client进行数据回环测试。 连接方式 使开发板和我们的电脑处于同一网段: 开发板通过交叉线直连主机开发板和主机都接在路由器LAN口 测试工具 网路调试工具&a…...
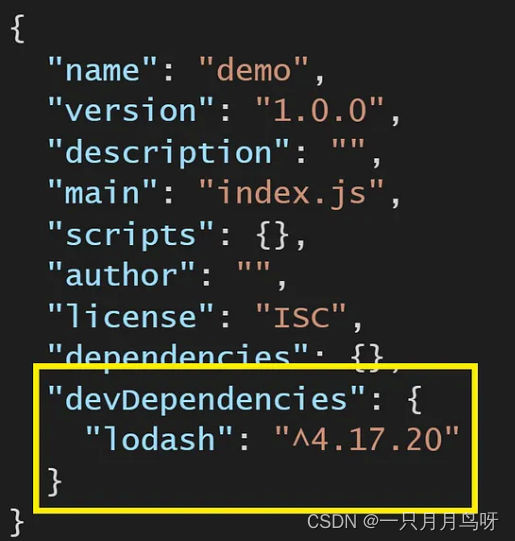
npm install 中 --save 和 --save-dev 是什么?
npm,全名 Node Package Manager,套件管理工具,package.json 会记下你在项目中安装的所有套件。 假设在项目中安装 lodash npm i --save lodash这样在 dependencies 中会出现: 如果修改了导入方式: npm i --save-dev …...

【Nginx17】Nginx学习:目录索引、字符集与浏览器判断模块
Nginx学习:目录索引、字符集与浏览器判断模块 今天要学习的内容有几个还是大家比较常见的,所以学习起来也不会特别费劲。对于目录的默认页设置大家都不会陌生,字符集的设置也比较常见,而浏览器的判断这一块,可能有同学…...

CA/TA开发编程实战-视频课程
Hello大家好,上架一门新的视频课程,课程主要包含两大部分,第一部分搭建环境,第二部分从无到有的编写代码。带领大家"手把手"编写。 具体大纲如下: qemu v8环境搭建 搭建一个qemu_v8的环境,用于…...

(7)(7.1) 使用航点和事件规划任务
文章目录 前言 7.1.1 设置Home位置 7.1.2 视频:制作并保存多路点任务 7.1.3 视频:加载已保存的多航点任务 7.1.4 使用说明 7.1.5 提示 7.1.6 自动网格 7.1.7 任务指令 7.1.8 任务结束 7.1.9 任务重置 7.1.10 MIS_OPTIONS 7.1.11 任务再出发 …...

OCR相关模块——版面分析技术、表格文本识别
OCR相关模块——版面分析技术、表格文本识别 版面分析技术表格识别技术 版面分析技术 版面分析模型:飞桨用到了yolov2检测模型,对文档图片中的文本、表格、图片、标题与列表区域进行检测。当前主流是用分割做。 表格识别技术 参考博文...
mov转mp4格式怎么转?
mov转mp4格式怎么转?众所周知,MOV视频格式是由苹果公司推出的常用的视频格式,能够在苹果软件及设备上使用。但是,如果将其应用于其他软件和设备上的话,可能会遇到文件无法正常播放的情况。在这个时候,我们需…...
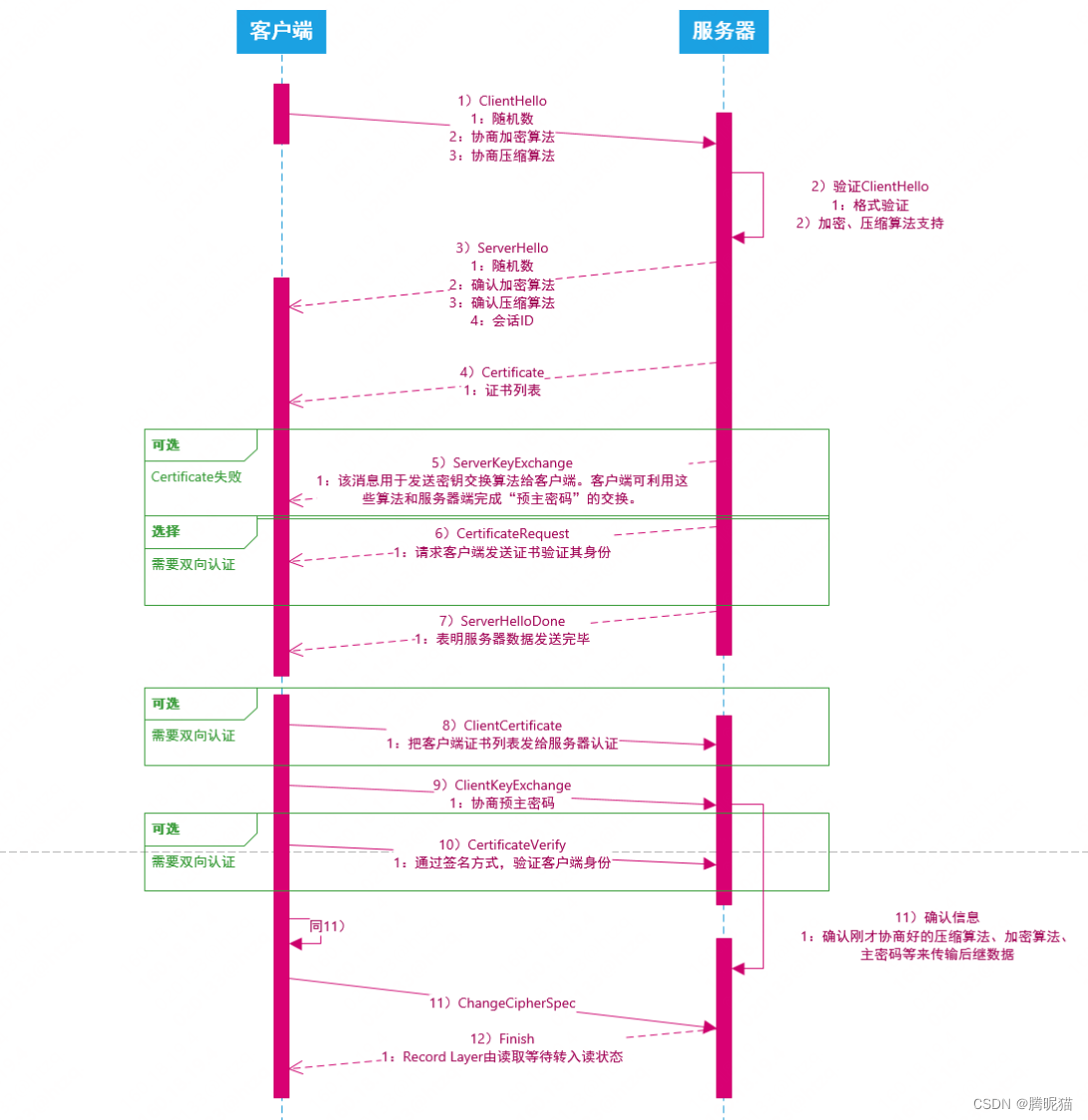
SSL握手协议相关概念
下图为握手协议的流程图,具体的解释参考博客: 【下】安全HTTPS-全面详解对称加密,非对称加密,数字签名,数字证书和HTTPS_tenfyguo的博客-CSDN博客 下面梳理一下SSL协议中的一些细节。首先是相关名词:证书、…...

idea 打开java项目后新建的模块中,java文件夹需要变成蓝色,以及resources文件夹变成三条杠的
idea 打开java项目后新建的模块中,java文件夹需要变成蓝色,以及resources文件夹变成三条杠的方法 再选择modules,找到需要变蓝的文件夹,点击sources即可 同理resources文件夹变成三条杠也只需要找到对应文件夹,点击re…...

【Docker】Docker network之bridge、host、none、container以及自定义网络的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...
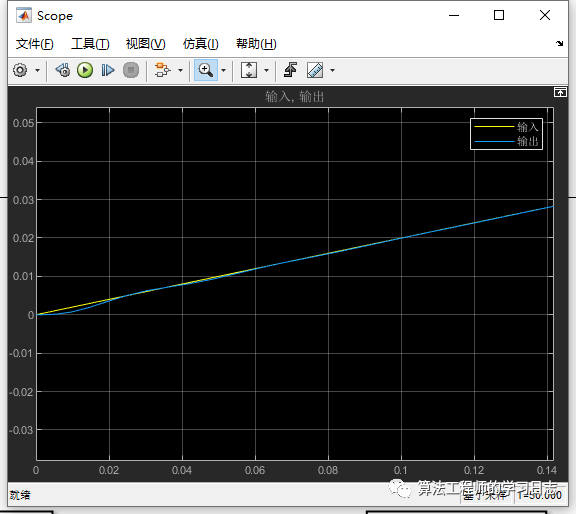
滑模控制器理论推导和matlab/simulink实例分享
滑模控制的运动轨迹主要分为两个方面:(1)系统的任意初始状态向滑模面运动阶段;(2)系统到达滑模面后并且慢慢趋于稳定的阶段。所以,对于滑模变结构控制器的设计,对应于系统运动的两个阶段,可以分为两个部分:…...

git 操作
git切换ssh和http协议 切换协议: 查看当前remote git remote -v 切换到http: git remote set-url https://github.com/username/repository.git 切换到ssh: git remote set-url gitgithub.com:username/repository.git 某些文件不想提交…...
自建hexo博客并将原有的文章发布其上
1、保存粘贴到memo9中的博客文章,并将txt转换成word文档 varPowerShellPath, CommandLine: string; // , ScriptPath begin//save to txtMemo9.Lines.SaveToFile(test.txt);memo10.Lines.SaveToFile(txt2word.ps1);//save as docxPowerShellPath : powershell.exe…...

【双指针_和为 s 的两个数_C++】
和为s的两个数字 class Solution { public:vector<int> twoSum(vector<int>& nums, int target) {int n nums.size();int left 0;int right n-1;while(left<right){if(nums[left]nums[right]>target) right--;else if(nums[left]nums[right]<tar…...
HTML5的介绍和基本框架
目录 HTML5 HTML5介绍 HTML5的DOCTYPE声明 HTML5基本骨架 html标签 head标签 body标签 title标签 meta标签 在vscode中写出第一个小框架 HTML5 HTML5介绍 HTML5是用来描述网页的一种语言,被称为超文本标记语言。用HTML5编写的文件,后缀以.ht…...
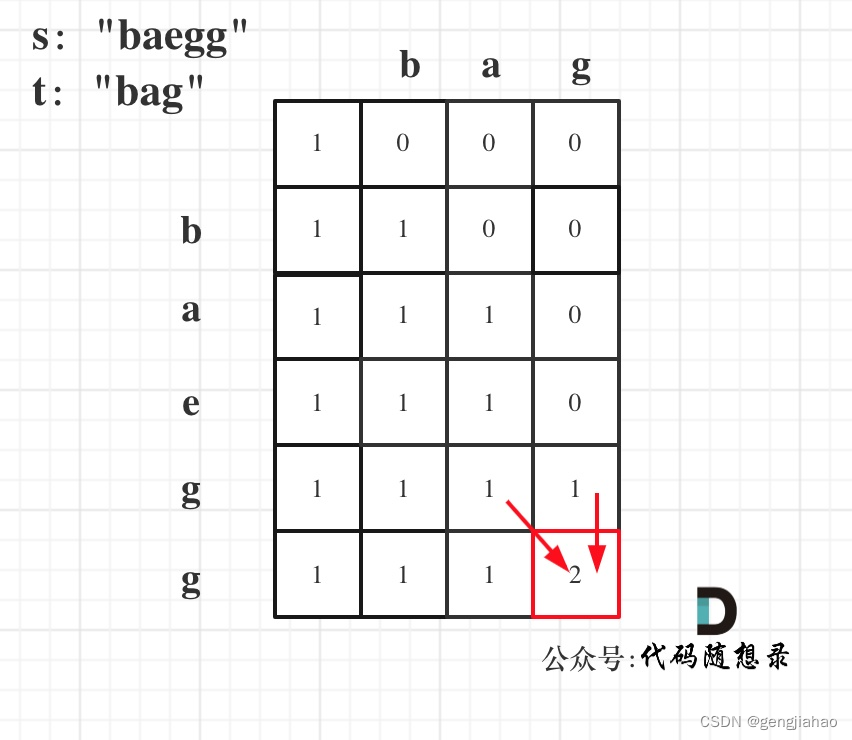
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列
代码随想录算法训练营第58天|动态规划part15|392.判断子序列、115.不同的子序列 392.判断子序列 392.判断子序列 思路: (这道题也可以用双指针的思路来实现,时间复杂度也是O(n)) 这道题应该算是编辑距…...

日常BUG——普通页面跳转tabbar页面报错
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 微信小程序页面跳转的时候出现下面的问题: wx.redirectTo({url: /pages/index/i…...
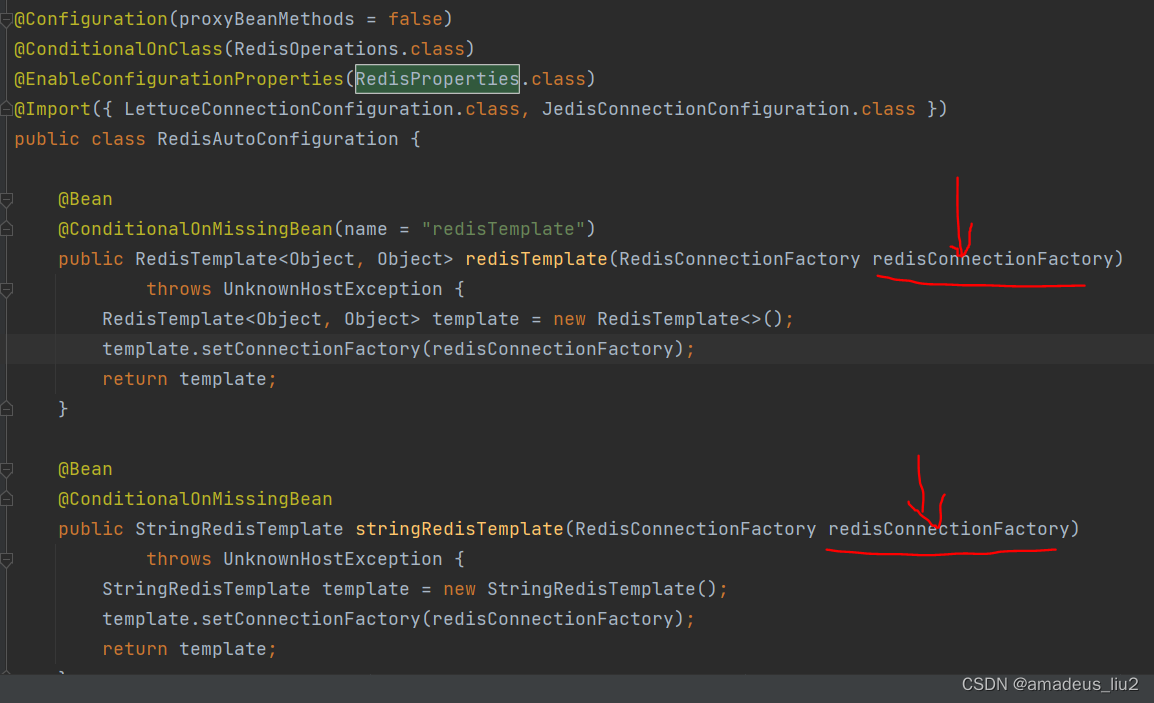
SpringBoot复习:(48)RedisAutoConfiguration自动配置类
RedisAutoConfiguration类代码如下: 可以看到在这个类中配置了2个bean: redisTemplate和stringRedisTemplate. 而它通过EnableConfigurationProperties(RedisProperties.class)注解,把配置文件中配置的Redis相关的信息引入进来了,RedisPrope…...

软硬件免费,服务收费:网络安全商业模式正在被颠覆
大数据产业创新服务媒体 ——聚焦数据 改变商业 从元宇宙到造汽车,重回国内A股市场五年的360一路苦追热点。一直到大模型横空出世,360才算真正找到感觉,经历一次战略上的回归。 在8月9日的互联网安全大会上,一袭红衣的红衣教主周…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...
