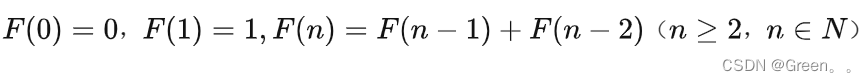函数递归专题(案例超详解一篇讲通透)
函数递归
- 前言
- 1.递归案例:
- 案例一:取球问题
- 案例二:求斐波那契额数列
- 案例三:函数实现n的k次方
- 案例四:输入一个非负整数,返回组成它的数字之和
- 案例五:元素逆置
- 案例六:实现strlen
- 案例七:爬楼梯1.0
- 案例八:爬楼梯2.0
- 案例九:求阶乘
- 案例十:求阶乘和
- 案例十一:杨辉三角
- 案例十二:最大公约数
- 案例十四:汉偌塔
- 2.递归与迭代
- 3.何时使用递归
前言
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。
一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
递归策略
只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小
递归的两个必要条件
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件
1.递归案例:
案例一:取球问题
在 n 个球中,任意取 m 个(不放回),求有多少种不同取法。
分析:
假设有一个特殊球,此球的状态只有两种:被取到和没有被取到。
若被取到,那么只需在n-1个球中取m-1个球。
若没有被取到,需在n-1个球中取m个球。
代码演示:
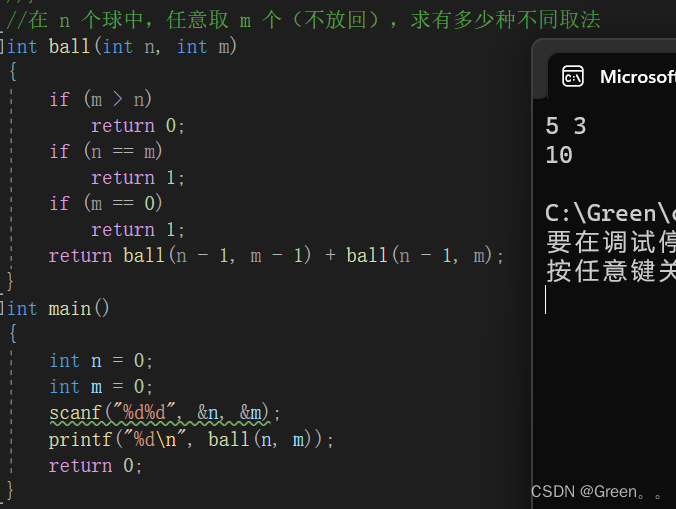
int ball(int n, int m)
{if (m > n)return 0;if (n == m)return 1;if (m == 0)return 1;return ball(n - 1, m - 1) + ball(n - 1, m);
}
int main()
{int n = 0;int m = 0;scanf("%d%d", &n, &m);printf("%d\n", ball(n, m));return 0;
}
运行结果:
案例二:求斐波那契额数列
这个数列从第3项开始,每一项都等于前两项之和。
分析:
在数学上,斐波那契数列以如下被以递推的方法定义:
代码演示:
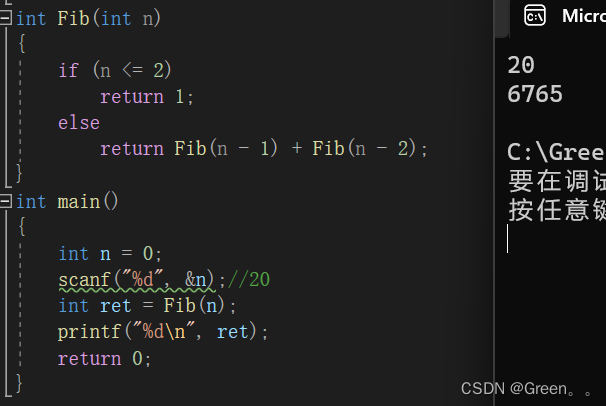
int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);//20int ret = Fib(n);printf("%d\n", ret);return 0;
}
运行结果:
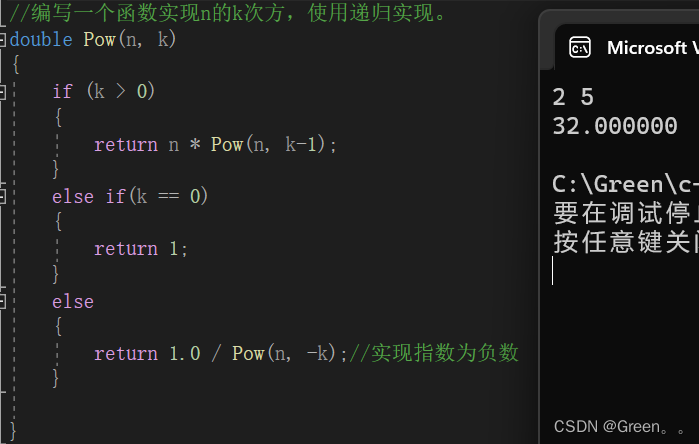
案例三:函数实现n的k次方
分析
指数为负数用double(%lf打印)
代码演示:
double Pow(n, k)
{if (k > 0){return n * Pow(n, k-1);}else if(k == 0){return 1;}else{return 1.0 / Pow(n, -k);//实现指数为负数}}
int main()
{int n = 0;int k = 0;scanf("%d %d", &n, &k);double ret = Pow(n, k);printf("%lf\n", ret);//double打印用lfreturn 0;
}
运行结果:
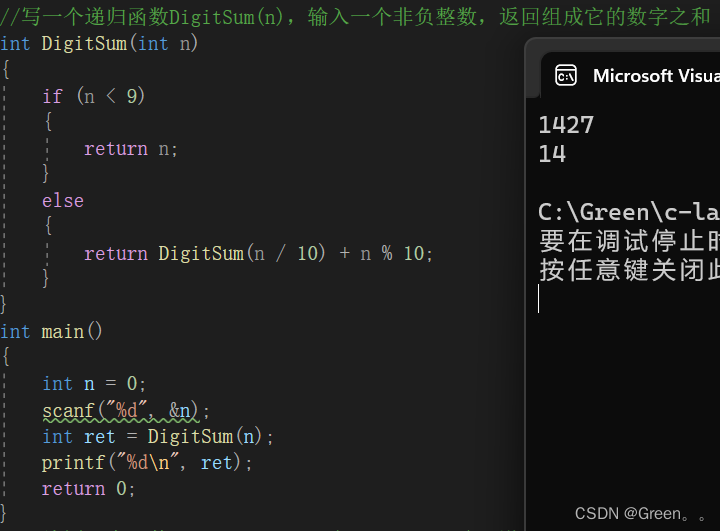
案例四:输入一个非负整数,返回组成它的数字之和
分析:
当一个数是大于0 的数时,要得结果等于这个数模(%)10得到最低位的数字,然后再加它的次低位…一直加到最高位的数字,这些数字用给这个数除以(10)得到,递归调用这个函数,即可。
代码演示:
int DigitSum(int n)
{if (n < 9){return n;}else{return DigitSum(n / 10) + n % 10;}
}
int main()
{int n = 0;scanf("%d", &n);int ret = DigitSum(n);printf("%d\n", ret);return 0;
}
运行结果:
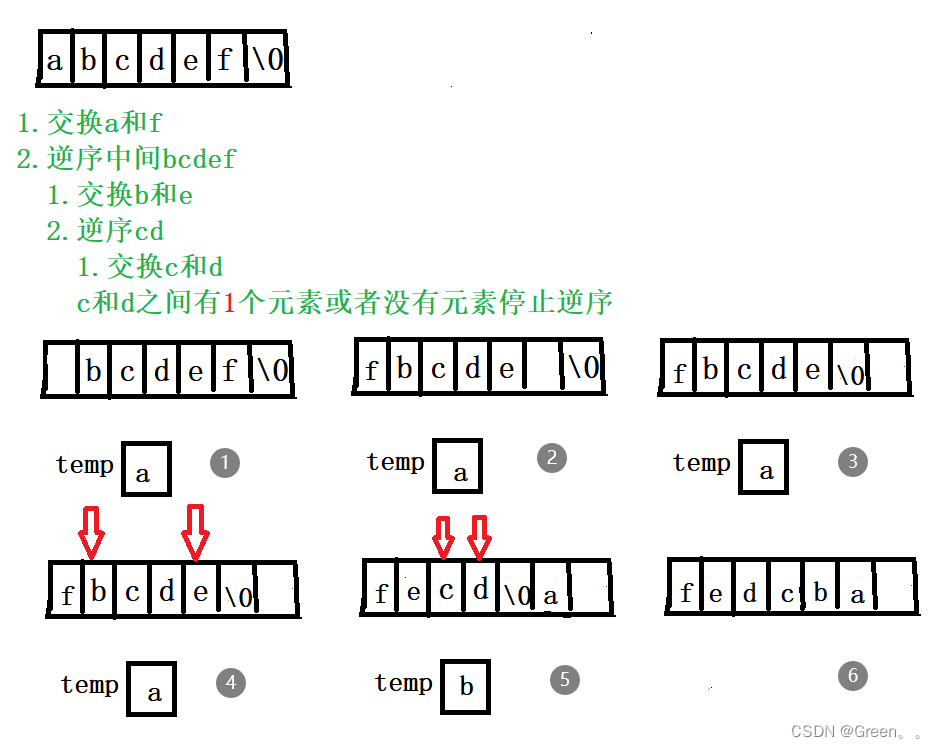
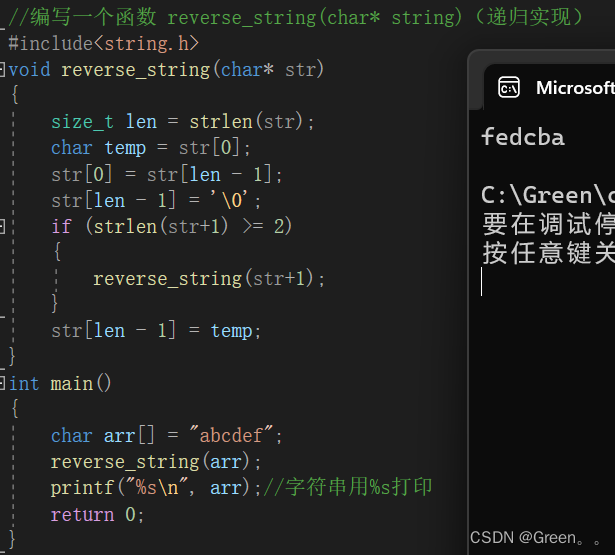
案例五:元素逆置
分析:
代码演示:
#include<string.h>
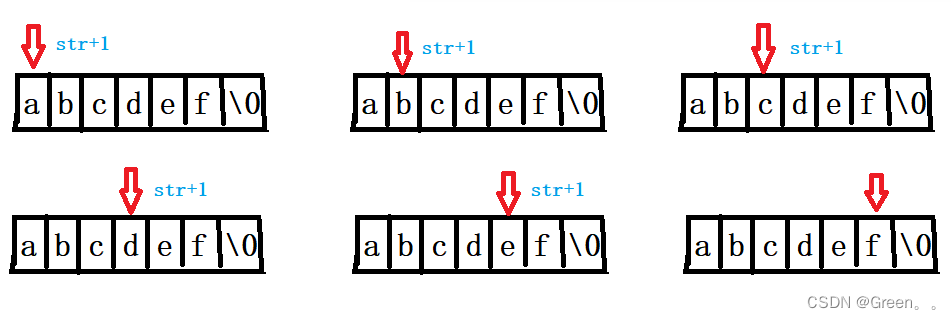
void reverse_string(char* str)
{size_t len = strlen(str);char temp = str[0];str[0] = str[len - 1];str[len - 1] = '\0';if (strlen(str+1) >= 2){reverse_string(str+1);}str[len - 1] = temp;
}
int main()
{char arr[] = "abcdef";reverse_string(arr);printf("%s\n", arr);//字符串用%s打印return 0;
}
运行结果:
案例六:实现strlen
分析:
代码演示:
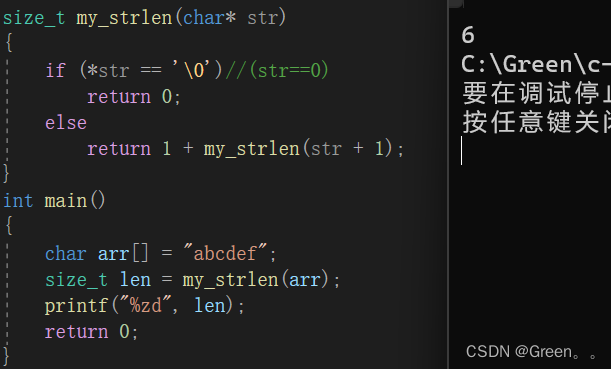
size_t my_strlen(char* str)
{if (*str == '\0')//(str==0)return 0;elsereturn 1 + my_strlen(str + 1);
}
int main()
{char arr[] = "abcdef";size_t len = my_strlen(arr);printf("%zd", len);return 0;
}
运行结果:
案例七:爬楼梯1.0
树老师爬楼梯,他可以每次走 1 级或者 2 级,输入楼梯的级数,求不同的走法数。
分析:
如果从第0级台阶爬到第1级台阶:有1种方法(爬1个台阶)
如果从第0级台阶爬到第2级台阶:有2种方法(爬1个台阶 或 爬2个台阶)
如果从第0级台阶爬到第3级台阶:有3种方法
先从第0级台阶爬到第1级台阶,再从第1级台阶爬到2级台阶,再从第2级台阶爬到第3级台阶,即1,1,1
先从第0级爬1个台阶到第1级台阶,再从第1级爬2个台阶到第3级,即1,2
先从第0级爬2个台阶到第2级台阶,再从第2级爬1个台阶到第3级,即2,1
如果从第0台阶爬到第4级台阶:有5种方法
1,1,1,1
1,1,2
1,2,1
2,1,1
2,2
归纳发现原理同:斐波那契数列
代码演示:
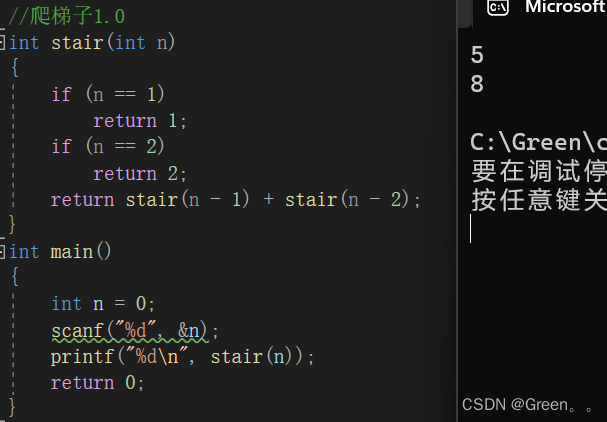
int stair(int n)
{if (n == 1)return 1;if (n == 2)return 2;return stair(n - 1) + stair(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);printf("%d\n", stair(n));return 0;
}
运行结果:
案例八:爬楼梯2.0
树老师爬楼梯,他可以每次走 1 级、2 级或者 3 级,输入楼梯的级数,求不同的走法数。
原理同上
代码演示:
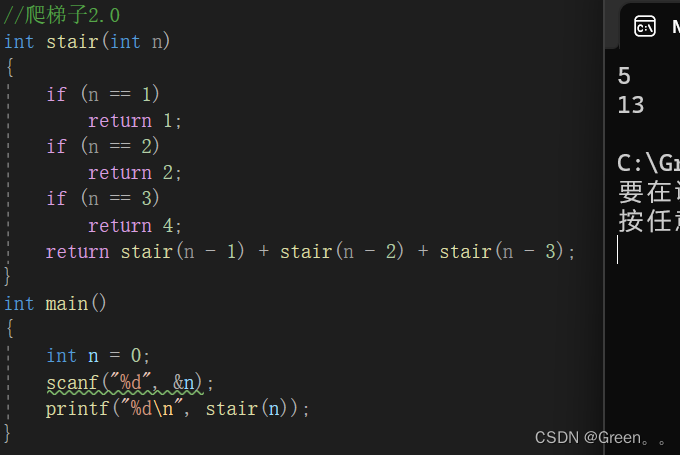
int stair(int n)
{if (n == 1)return 1;if (n == 2)return 2;if (n == 3)return 4;return stair(n - 1) + stair(n - 2) + stair(n - 3);
}
int main()
{int n = 0;scanf("%d", &n);printf("%d\n", stair(n));
}
运行结果:
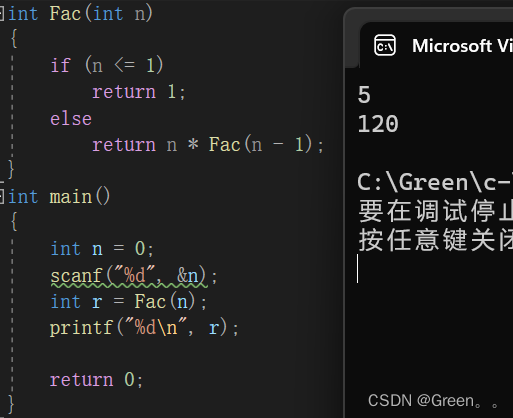
案例九:求阶乘
代码演示:
int Fac(int n)
{if (n <= 1)return 1;elsereturn n* Fac(n - 1);
}
int main()
{int n = 0;scanf("%d", &n);int r = Fac(n);printf("%d\n", r);return 0;
}
运行结果:
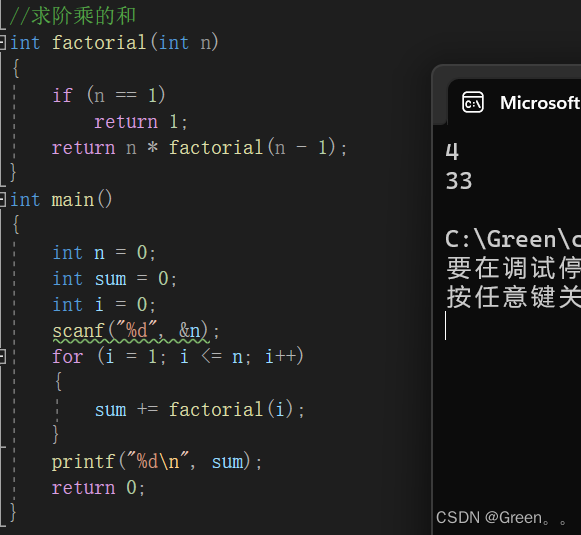
案例十:求阶乘和
求 1!+2!+3!+4!+5!+6!+7!+…+n!的和。
代码演示:
int factorial(int n)
{if (n == 1)return 1;return n * factorial(n - 1);
}
int main()
{int n = 0;int sum = 0;int i = 0;scanf("%d", &n);for (i = 1; i <= n; i++){sum += factorial(i);}printf("%d\n", sum);return 0;
}
运行结果:
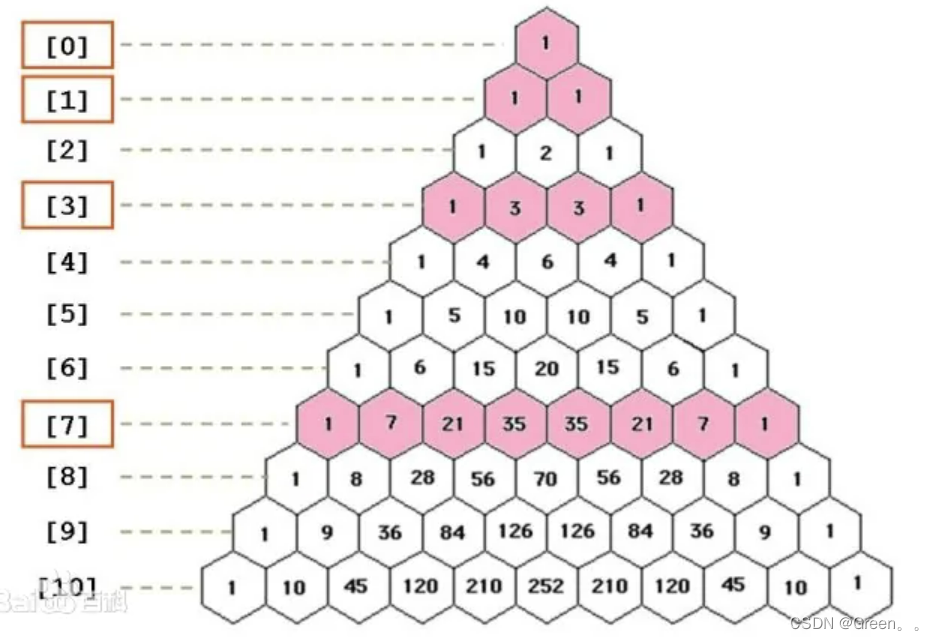
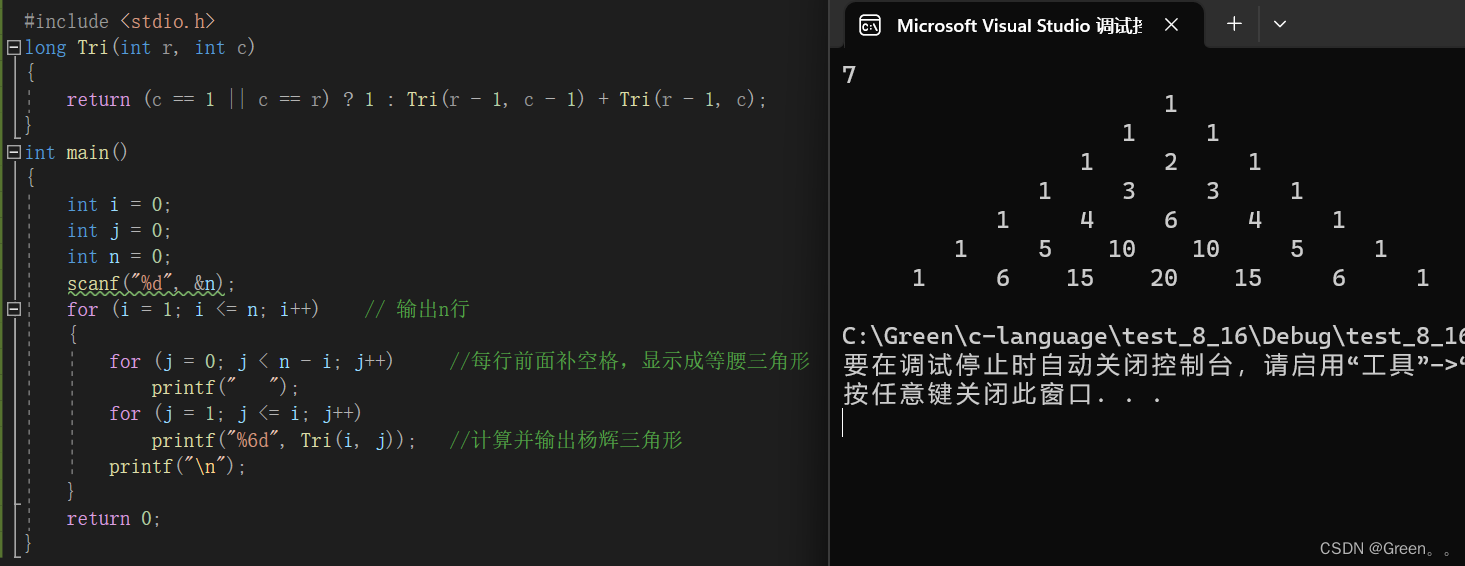
案例十一:杨辉三角
输入要打印的层数,打印杨辉三角
分析
根据观察第一列和对角线上的元素之外,其余元素的值均为前一行上的同列元素和前一列元素之和。(我们可以依靠递归相加就行实现)
#include <stdio.h>
long Tri(int r, int c)
{return (c == 1 || c == r) ? 1 : Tri(r - 1, c - 1) + Tri(r - 1, c);
}
int main()
{int i = 0;int j = 0;int n = 0;scanf("%d", &n);for (i = 1; i <= n; i++) // 输出n行{for (j = 0; j < n - i; j++) //每行前面补空格,显示成等腰三角形 printf(" ");for (j = 1; j <= i; j++)printf("%6d", Tri(i, j)); //计算并输出杨辉三角形 printf("\n");}return 0;
}
运行结果:
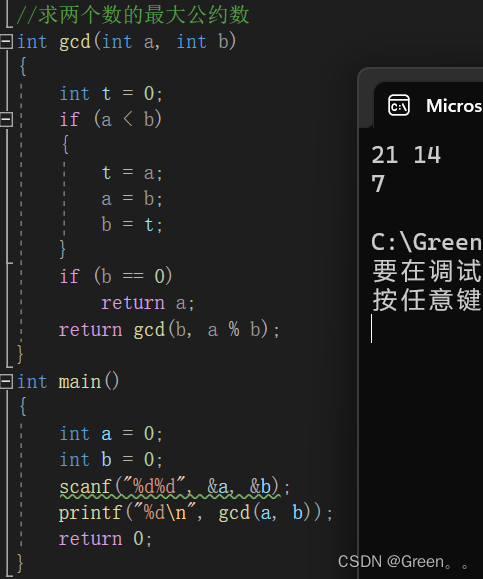
案例十二:最大公约数
//代码演示:
int gcd(int a, int b)
{int t = 0;if (a < b){t = a;a = b;b = t;}if (b == 0)return a;return gcd(b, a % b);
}
int main()
{int a = 0;int b = 0;scanf("%d%d", &a, &b);printf("%d\n", gcd(a, b));return 0;
}
运行结果:
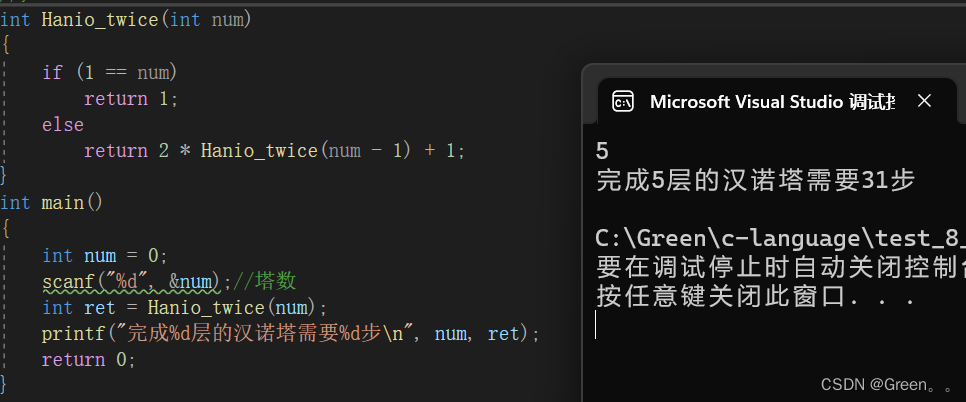
案例十四:汉偌塔
汉诺塔问题就是将A柱上n个圆全部移动到C上,过程中可以借助B柱,但要始终保持小圆在大圆上面
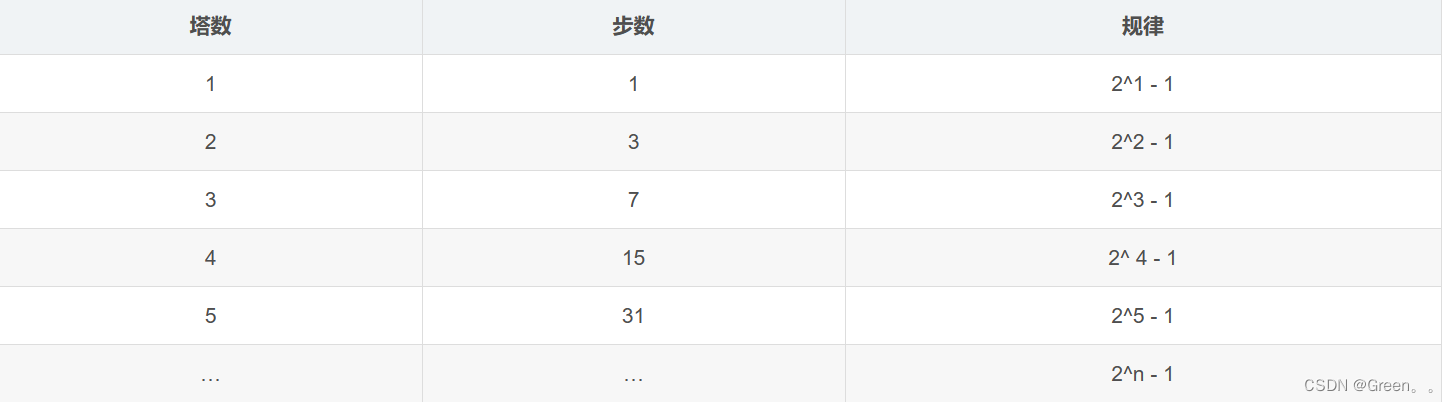
对于n阶汉诺塔的移动次数:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
int main()
{int num = 0;scanf("%d", &num);//塔数printf("完成%d层的汉诺塔需要%d步\n", num, (int)pow(2,num) - 1);return 0;
}
运行结果:
分析:
步骤1所含步数就是n-1个圆盘移动所需的次数,我们可以将其步数看做f(n-1)。
步骤2所含步数为1。
步骤3所含步数与步骤1相似,我们也将其步数看做f(n-1)。
再观察表格中汉诺塔的移动次数,对于一阶汉诺塔移动次数就为1,对于其他的阶数则为前一阶汉诺塔移动次数 + 1 + 前一阶汉诺塔移动次数。
不难得出递推表达式:f(n-1) + 1 + f(n-1) = 2 * f(n - 1) + 1
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int Hanio_twice(int num)
{if(1 == num)return 1;elsereturn 2 * Hanio_twice(num - 1) + 1;
}
int main()
{int num = 0; scanf("%d", &num);//塔数int ret = Hanio_twice(num);printf("完成%d层的汉诺塔需要%d步\n", num, ret);return 0;}
运行结果:
分析:
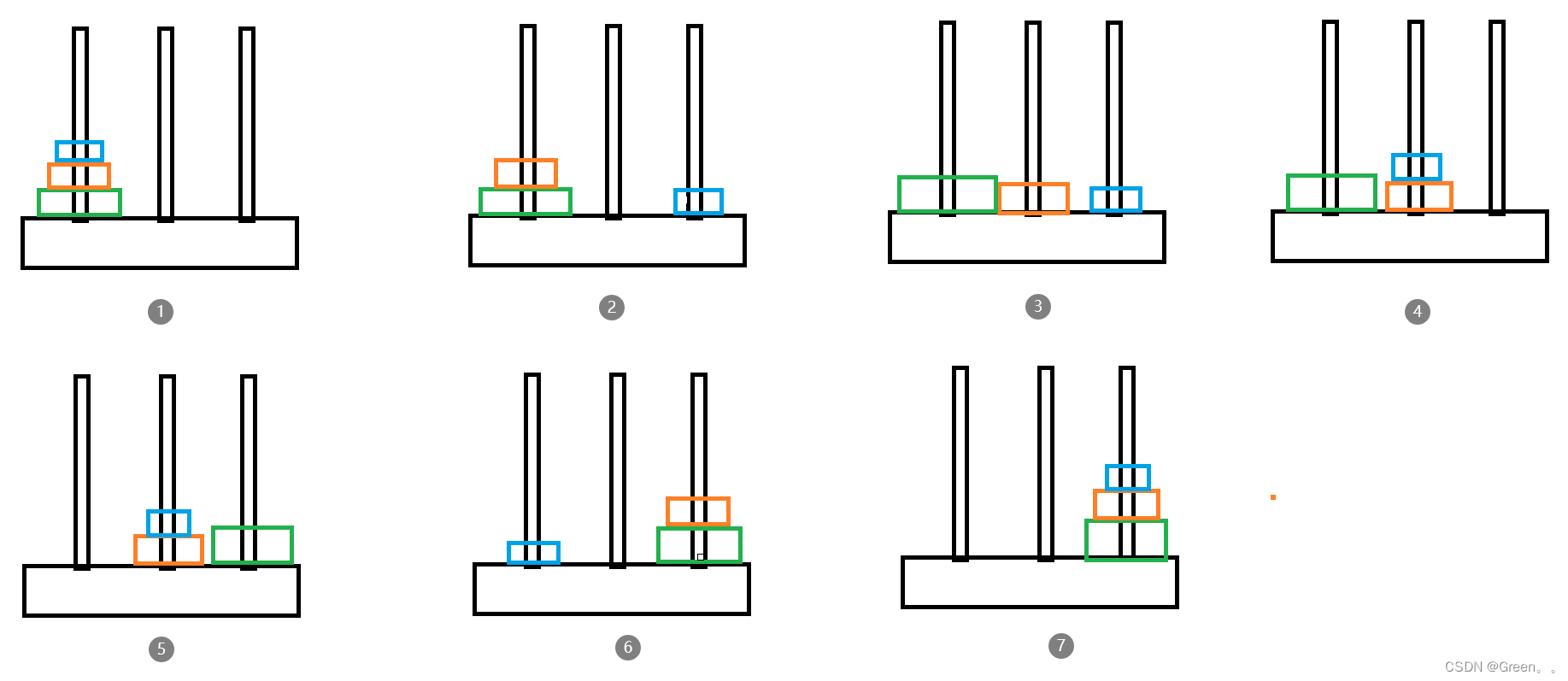
我们观察移动步骤,发现只有一个圆盘时移动步骤为A->C;两个圆盘时,为A->B,A->C,B->C。
那么对于n阶汉诺塔呢,我们对其进行推演:
1.把n-1个圆盘从A移动到B
2.把第n个圆盘从A移动到C
3.把n-1个圆盘从B移动到C
那n-1个圆盘如何从A移动到B呢?
1.把n-2个圆盘从A移动到C
2.把第n-1个圆盘从A移动到B
3.把n-2个圆盘从C移动到B
同样的,对于把n-1个圆盘从B移动到C,也可以推测出来:
1.把n-2个圆盘从B移动到A
2.把第n-1个圆盘从B移动到C
3.把n-2个圆盘从A移动到C
通过这些推演我们发现,汉诺塔的移动可以通过递归展开,那么以上推演步骤,我们可以将其作为递归的步骤。
思路:定义A,B,C三个字符,表示A,B,C三柱,定义n为阶数,那么n-1也就是移动步骤中,需要移动的圆盘数。
对于一阶汉诺塔,直接移动即可,对于其他的阶数,则需要通过递归展开,为n阶汉诺塔的移动步骤。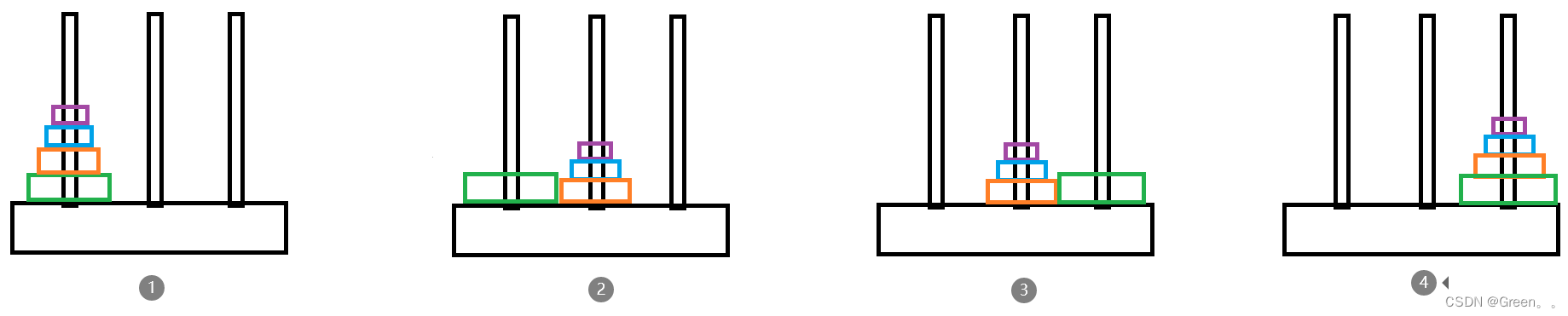
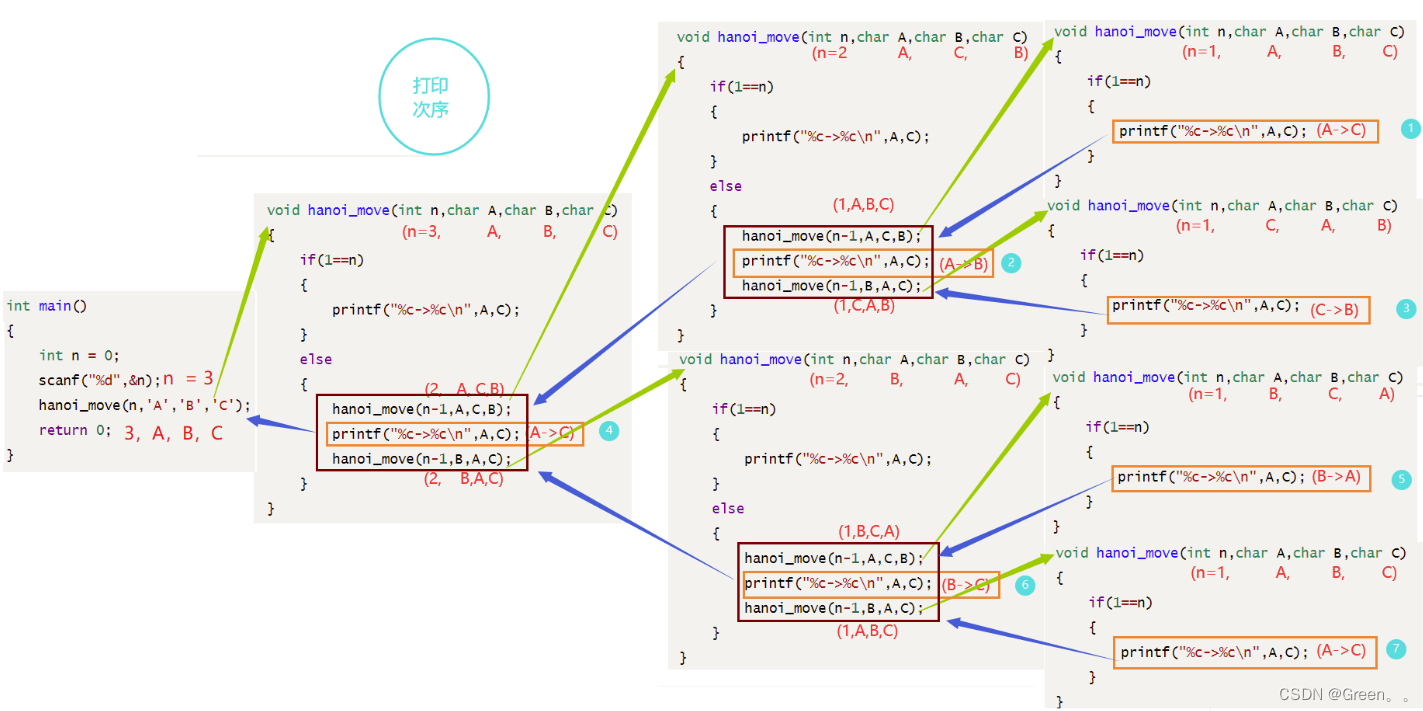
//代码演示:
void move(char pos1, char pos2)
{printf(" %c -> %c \n", pos1, pos2);
}
//pos1起始位置
//pos2中转位置
//pos3目标位置
void Hannoi(int n, char pos1, char pos2, char pos3)
{if (n == 1){move(pos1, pos3);}else{Hannoi(n - 1, pos1, pos3, pos2);move(pos1, pos3);Hannoi(n - 1, pos2, pos1, pos3);}
}
int main()
{/*Hannoi(1, 'A', 'B', 'C');*///Hannoi(2, 'A', 'B', 'C');Hannoi(3, 'A', 'B', 'C');return 0;
}
运行结果:
2.递归与迭代
听过上面函数递归案例发现有问题,如下:
在使用 Fib 这个函数的时候如果我们要计算第50个斐波那契数字的时候特别耗费时间。
使用 Fac 函数求10000的阶乘(不考虑结果的正确性),程序会崩溃。
为什么呢?
我们发现 Fib 函数在调用的过程中很多计算其实在一直重复。
那我们如何改进呢?
在调试 Fac 函数的时候,如果你的参数比较大,那就会报错: **stack overflow(栈溢出)**这样的信息。
系统分配给程序的栈空间是有限的,但是如果出现了死循环,或者(死递归),这样有可能导致一直开辟栈空间,最终产生栈空间耗尽的情况,这样的现象我们称为栈溢出。
那如何解决上述的问题:
将递归改写成非递归。
使用static对象替代 nonstatic 局部对象。在递归函数设计中,可以使用 static 对象替代nonstatic 局部对象(即栈对象),这不仅可以减少每次递归调用和返回时产生和释放 nonstatic 对象的开销,而且 static 对象还可以保存递归调用的中间状态,并且可为各个调用层所访问。
比如,下面代码就采用了,非递归的方式来实现:
n的阶乘
int Fac(int n)
{int i = 0;int r = 1;for (i = 1; i <= n; i++){r = r * i;}return r;
}
int main()
{int n = 0;scanf("%d", &n);int r = Fac(n);printf("%d\n", r);return 0;
}
求第n个斐波那契数
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;scanf("%d", &n);//20int ret = Fib(n);printf("%d\n", ret);return 0;
3.何时使用递归
如果使用递归很容易想到,写出的代码没有明显的缺陷,那我们就可以使用递归
但如果写出的递归代码,有明显问题,比如:栈溢出,效率低下等,那我们还是使用迭代的方式来解决.
💘本次专题已结束,不久将来会有更多专题与大家见面!!!
相关文章:
函数递归专题(案例超详解一篇讲通透)
函数递归 前言1.递归案例:案例一:取球问题案例二:求斐波那契额数列案例三:函数实现n的k次方案例四:输入一个非负整数,返回组成它的数字之和案例五:元素逆置案例六:实现strlen案例七:…...

leetcode-413. 等差数列划分(java)
等差数列划分 leetcode-413. 等差数列划分题目描述双指针 上期经典算法 leetcode-413. 等差数列划分 难度 - 中等 原题链接 - 等差数列划分 题目描述 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如࿰…...
从零开始学习 Java:简单易懂的入门指南之MAth、System(十二)
常见API,MAth、System 1 Math类1.1 概述1.2 常见方法1.3 算法小题(质数)1.4 算法小题(自幂数) 2 System类2.1 概述2.2 常见方法 1 Math类 1.1 概述 tips:了解内容 查看API文档,我们可以看到API文档中关于Math类的定义如下: Math类…...
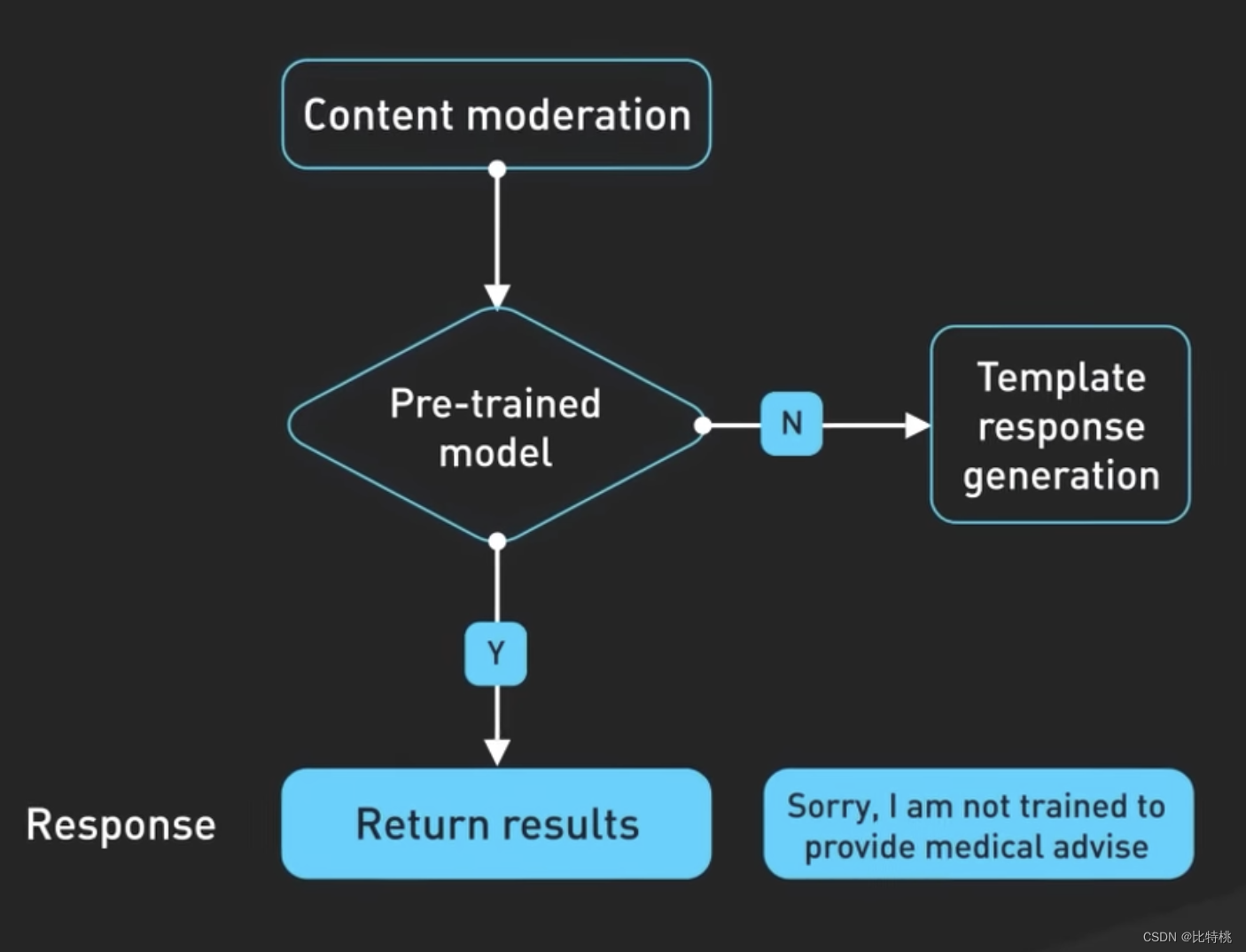
人工智能原理概述 - ChatGPT 背后的故事
大家好,我是比特桃。如果说 2023 年最火的事情是什么,毫无疑问就是由 ChatGPT 所引领的AI浪潮。今年无论是平日的各种媒体、工作中接触到的项目还是生活中大家讨论的热点,都离不开AI。其实对于互联网行业来说,自从深度学习出来后就…...
【Linux】以太网协议——数据链路层
链路层解决的问题 IP拥有将数据跨网络从一台主机送到另一台主机的能力,但IP并不能保证每次都能够将数据可靠的送到对端主机,因此IP需要上层TCP为其提供可靠性保证,比如数据丢包后TCP可以让IP重新发送数据,最终在TCP提供的可靠性机…...

Neo4j之MATCH基础
1】基本匹配和返回:查找所有节点和关系,返回节点的标签和属性。 MATCH (n) RETURN n;2】条件筛选:查找所有名为 "Alice" 的人物节点。 MATCH (person:Person {name: Alice}) RETURN person;3】关系查询:查找所有和 &q…...
Python实验代码合集
NumPy实验(1) NumPy实验(2) NumPy实验(3) SciPy实验(1) 请结合最小二乘法的原理,利用以前学的Numpy和Python知识,实现最小乘法直线拟合的算法,并测试。 请结合梯度下降的原理,利用以前学的Numpy和Python知识,实现梯度下降法求函数最小值的…...

Less和Sass的原理和用法
一、原理 1.1 Less定义:是一种动态的样式语言,使CSS变成一种动态的语言特性,如变量、继承、运算、函数。Less既可以在客户端上面运行(支持IE6以上版本、Webkit、Firefox),也可以在服务端运行(Node.js) 1.2 SaSS定义:是一种动态样式语言&#…...

c# List<T>.Aggregate
List<T>.Aggregate 方法的定义: public TAccumulate Aggregate<TAccumulate>(TAccumulate seed, Func<TAccumulate, T, TAccumulate> func)参数解析如下: TAccumulate seed:初始累积值,也是累积的起始值(默认…...
软件测试常用工具总结(测试管理、单元测试、接口测试、自动化测试、性能测试、负载测试等)
前言 在软件测试的过程中,多多少少都是会接触到一些测试工具,作为辅助测试用的,以提高测试工作的效率,使用好了测试工具,能对测试起到一个很好的作用,同时,有些公司,也会要求掌握一…...

Hadoop组件
前言 Hadoop 是一个能够对大量数据进行分布式处理的软件框架。具有可靠、高效、可伸缩的特点。 HDFS(hadoop分布式文件系统) 是hadoop体系中数据存储管理的基础。他是一个高度容错的系统,能检测和应对硬件故障。 Mapreduce(分…...
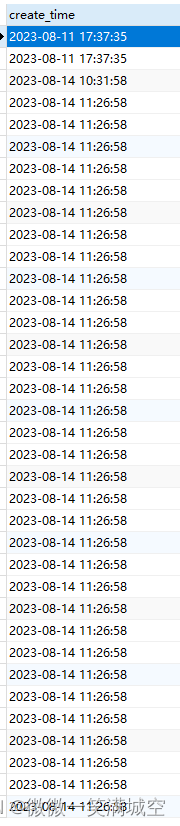
jeecg-boot批量导入问题注意事项
现象: 由于批量导入数据速度很快, 因为数据库中的create time字段的时间可能一样,并且jeecg框架自带的是根据生成时间排序, 因此在前端翻页查询的时候,数据每次排序可能会不一样, 会出现第一页已经出现过一…...

Django图书商城系统实战开发 - 实现会员管理
Django图书商城系统实战开发 - 实现会员管理 在Django图书商城系统中,会员管理是一个重要的功能模块。该模块包括会员信息的展示、编辑和删除等功能。以下是实现会员管理功能的详细步骤和代码示例。 步骤一:设计数据库模型 首先,我们需要设…...

Kafka如何解决消息丢失的问题
在 Kafka 的整个架构中可以总结出消息有三次传递的过程: Producer 端发送消息给 Broker 端Broker 将消息进行并持久化数据Consumer 端从 Broker 将消息拉取并进行消费 在以上这三步中每一步都可能会出现丢失数据的情况, 那么 Kafka 到底在什么情况下才…...

我只记得512天在CSDN的日子
机缘 不知不觉开始写博客已经512天了,在这期间有过因为懒惰想要放弃,也有过写不出优质文章没有阅读量的气馁,也有过学习蛮久却不知道从何开始写起的迷茫,但是最终好在还是坚持了下来,无论好坏坚持总没有错。 写博客的…...

pycharm,VSCode 几个好用的插件
pycharm Tabnine AI Code 可以在编写程序的时候为你提供一些快捷方式,增加编程速度 Chinese 对英文不好的程序员来说是个不错的选择,可以将英文状态下的pycharm变为中文版的 ChatGPT 可以跟ai聊天,ai可以解决你80%的问题 ,也可以帮…...

springboot 使用zookeeper实现分布式ID
添加ZooKeeper依赖:在pom.xml文件中添加ZooKeeper客户端的依赖项。例如,可以使用Apache Curator作为ZooKeeper客户端库: <dependency><groupId>org.apache.curator</groupId><artifactId>curator-framework</arti…...

git cherry-pick
cherry-pick命令的基本用法 对于多分支的代码库,将代码从一个分支转移到另一个分支是常见需求。这时分两种情况。一种情况是,你需要另一个分支的所有代码变动,那么就采用合并( git merge )。另一种情况是,…...
转行软件测试四个月学习,第一次面试经过分享
我是去年上半年从销售行业转行到测试的,从销售公司辞职之后选择去培训班培训软件测试,经历了四个月左右的培训,在培训班结课前两周就开始投简历了,在结课的时候顺利拿到了offer。在新的公司从事软件测试工作已经将近半年有余&…...

ECS服务器安装docker
为了安装并配置 Docker ,你的系统必须满足下列最低要求: 64 位 Linux 或 Windows 系统 如果使用 Linux ,内核版本必须不低于 3.10 能够使用 sudo 权限的用户 在你系统 BIOS 上启用了 VT(虚拟化技术)支持 on your s…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...