Python实验代码合集
NumPy实验(1)

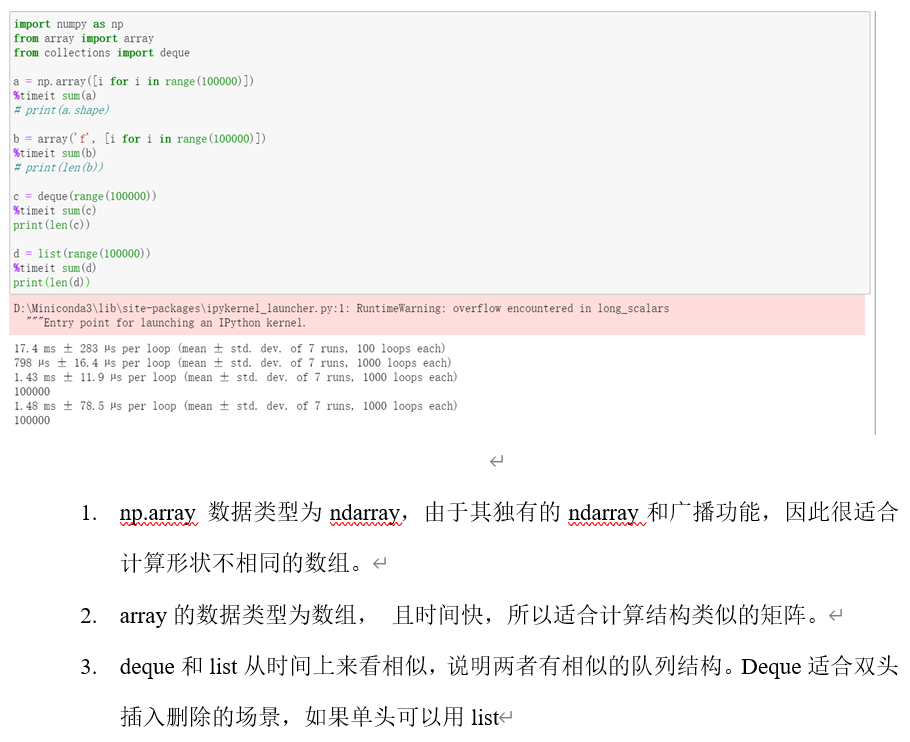
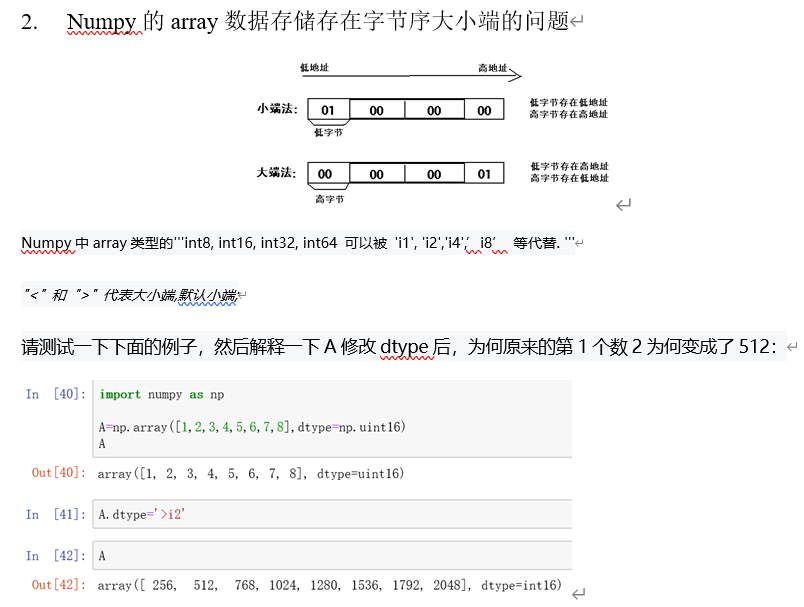



NumPy实验(2)
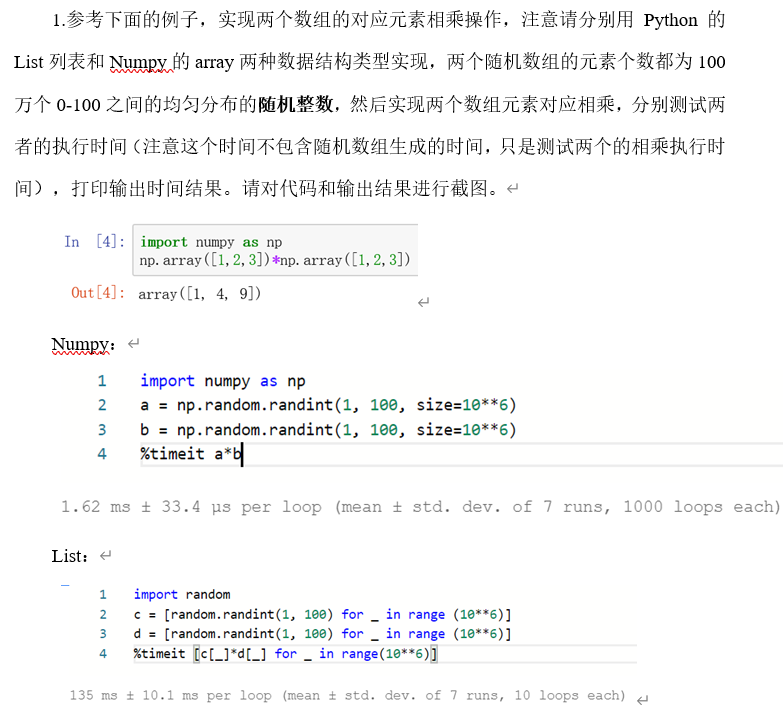


NumPy实验(3)
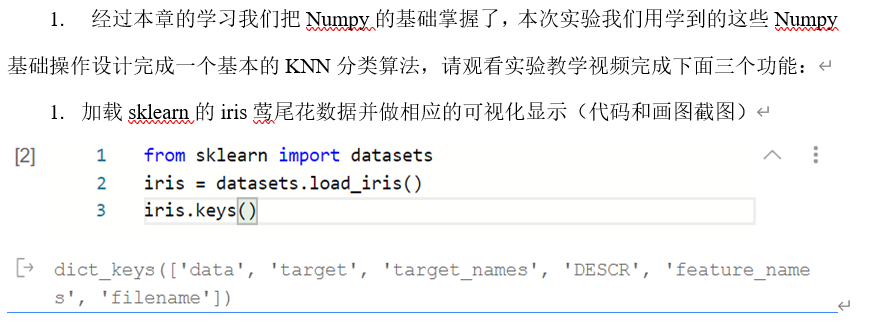

SciPy实验(1)
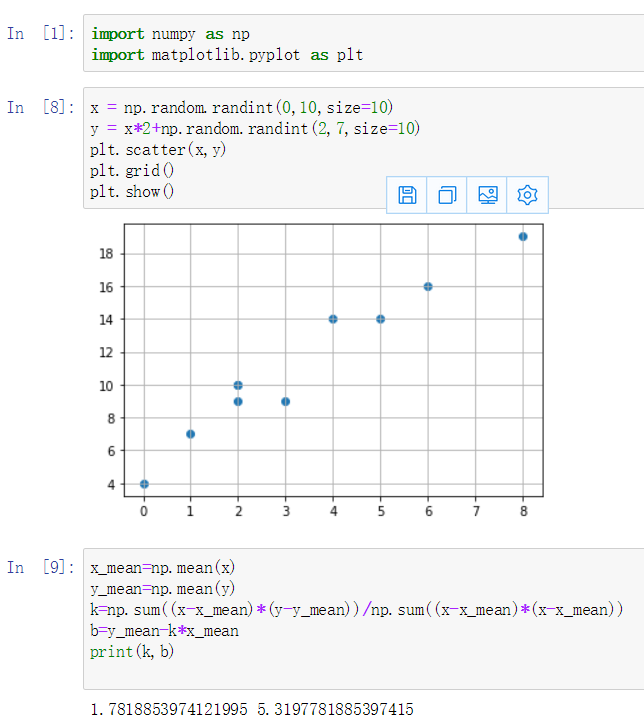
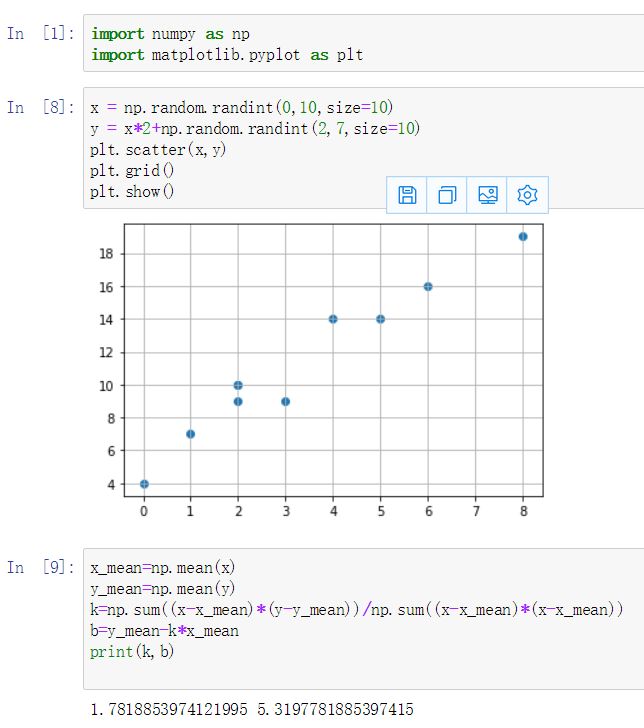
- 请结合最小二乘法的原理,利用以前学的Numpy和Python知识,实现最小乘法直线拟合的算法,并测试。
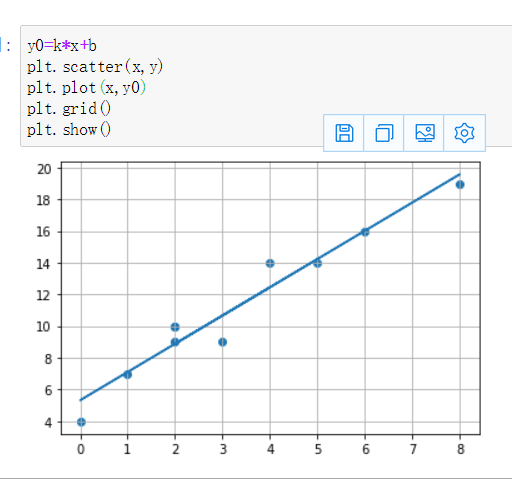
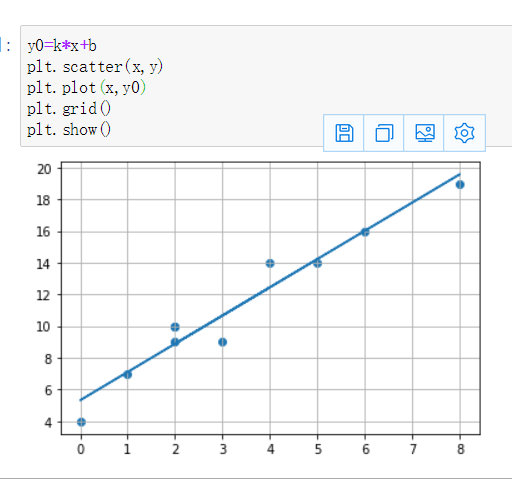
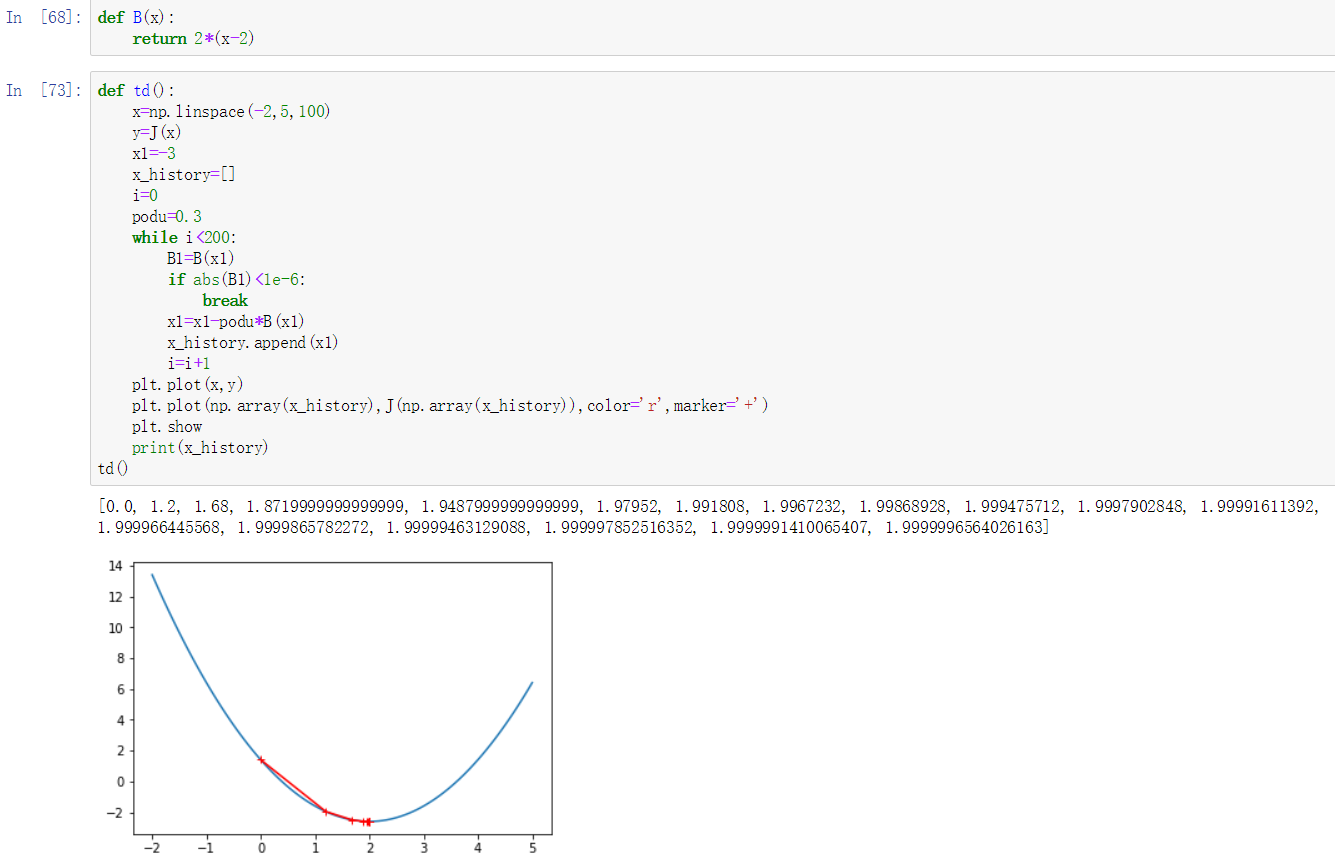
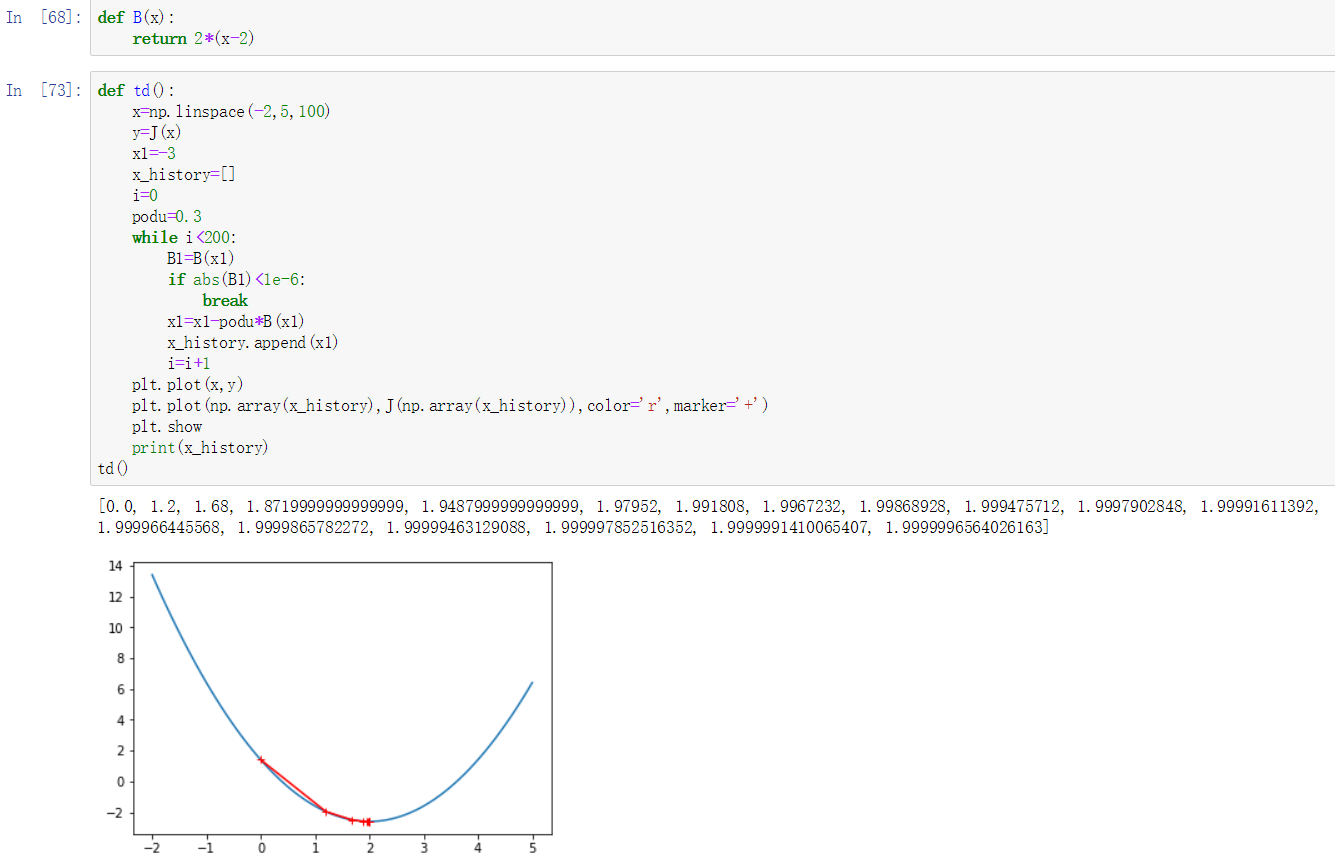
- 请结合梯度下降的原理,利用以前学的Numpy和Python知识,实现梯度下降法求函数最小值的算法,并测试。
- 梯度下降法:
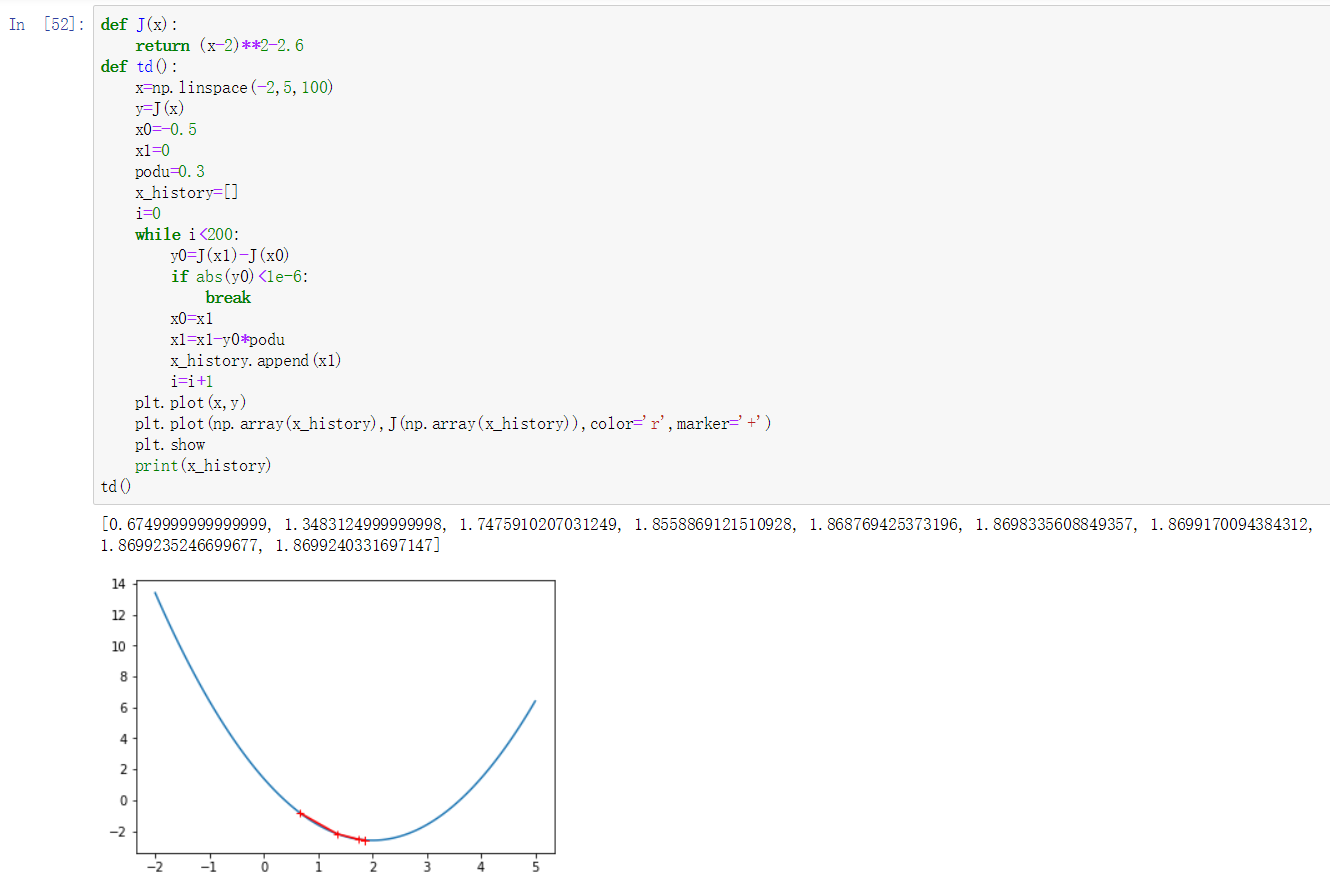
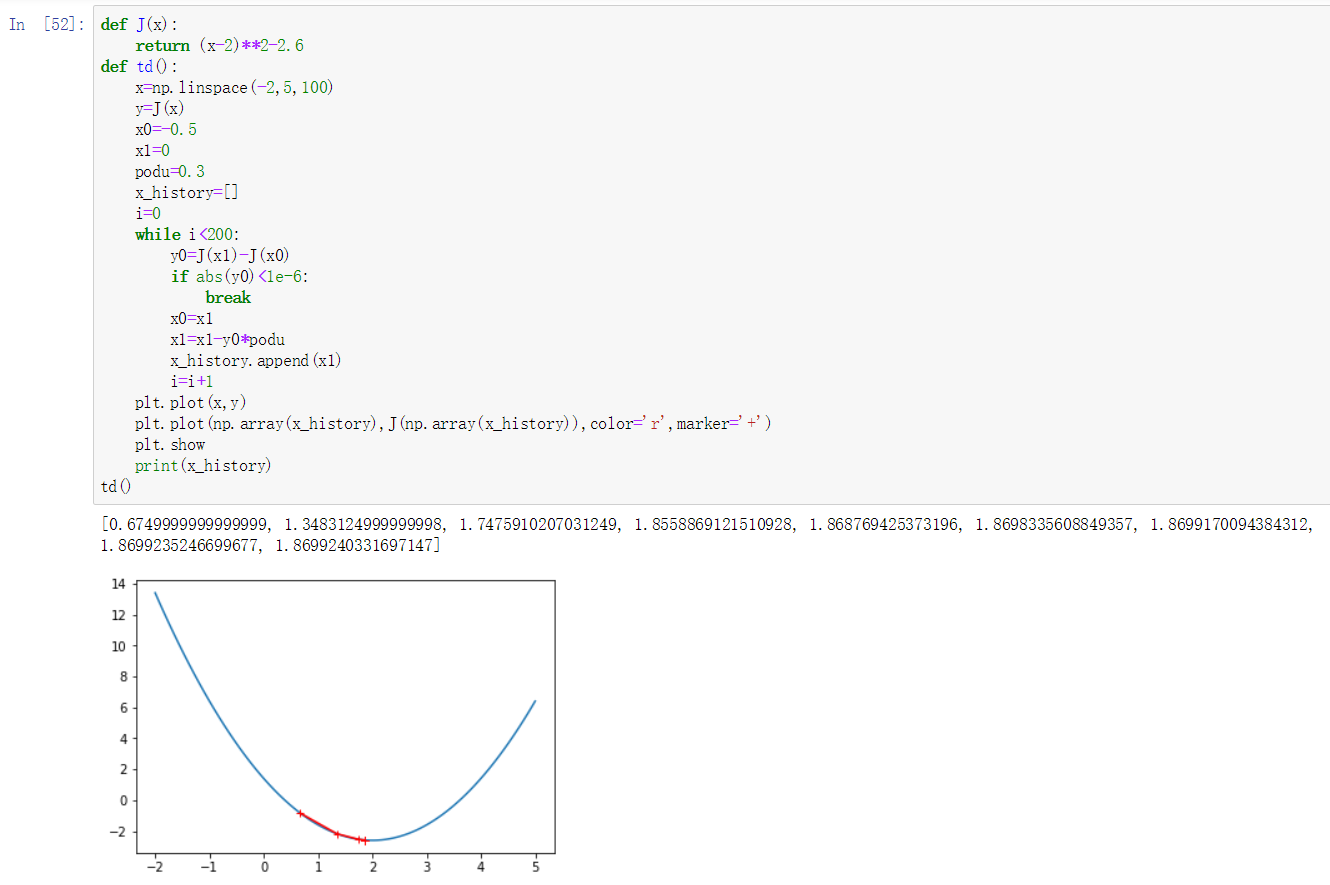
- 共轭梯度法:
SciPy实验(2)
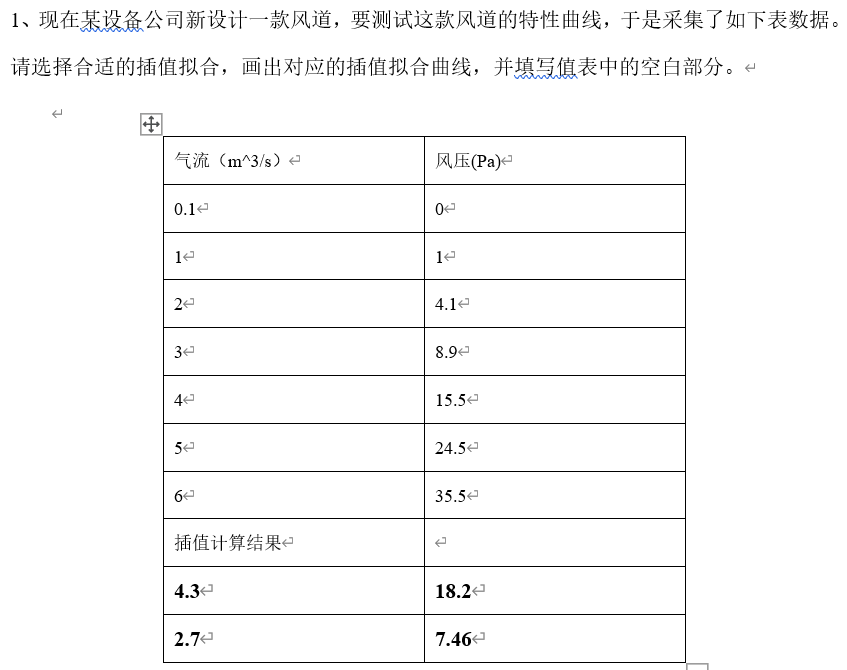
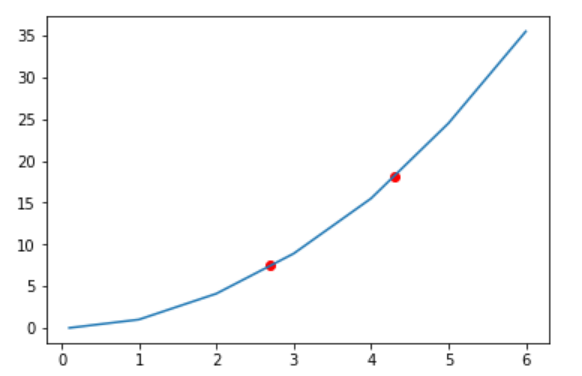
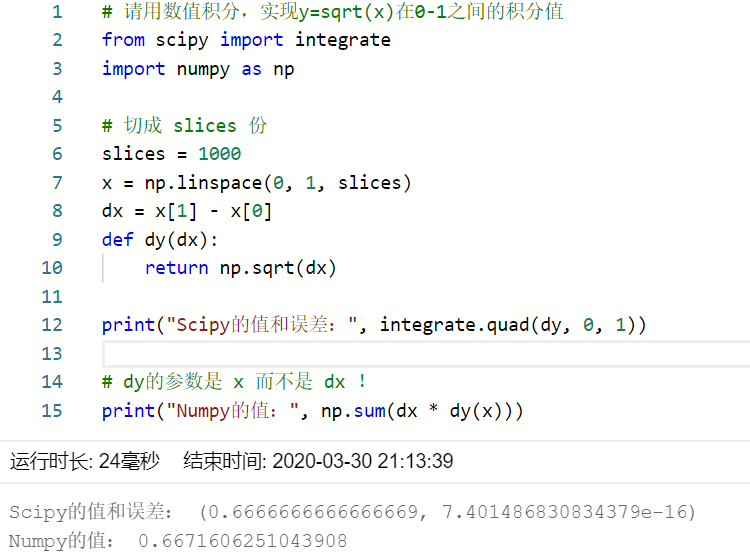
2.请用数值积分,实现y=sqrt(x)在0-1之间的积分值,写出代码和结果。
3.请结合scipy的矩阵svd分解,验证svd分解对图像压缩的实现效果。


SciPy实验(3)
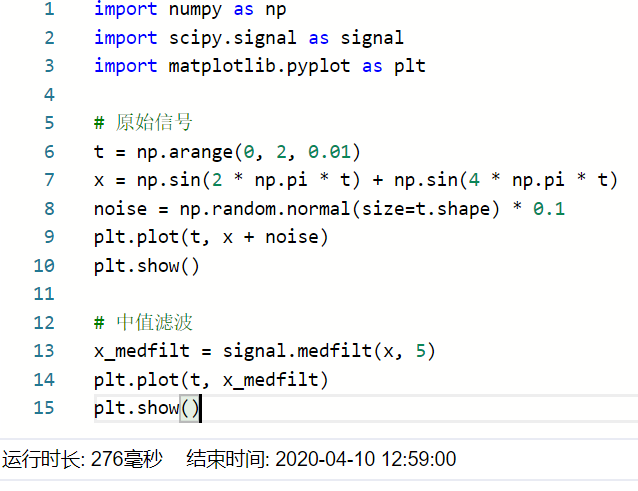
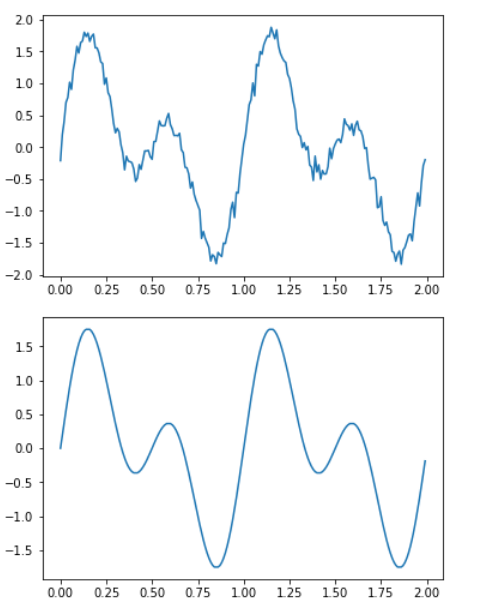
- 请生成y=sin(2*pi*t)+sin(4*pi*t)的时间信号,时间间隔10ms一个数据点,然后给这个信号注入0.1倍的标准正态分布噪声数据,然后设计滤波器将噪声滤除掉。列出代码和对比图。
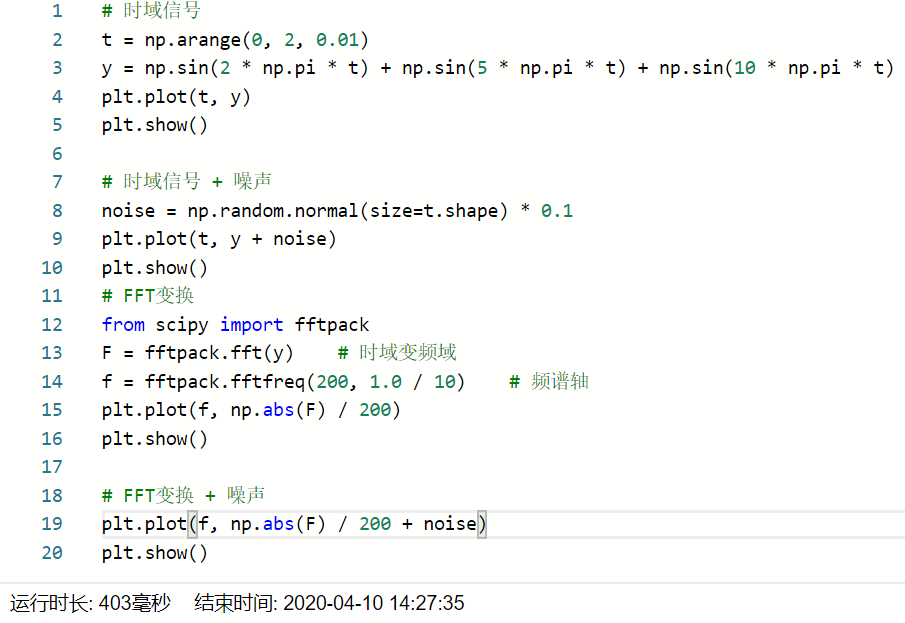
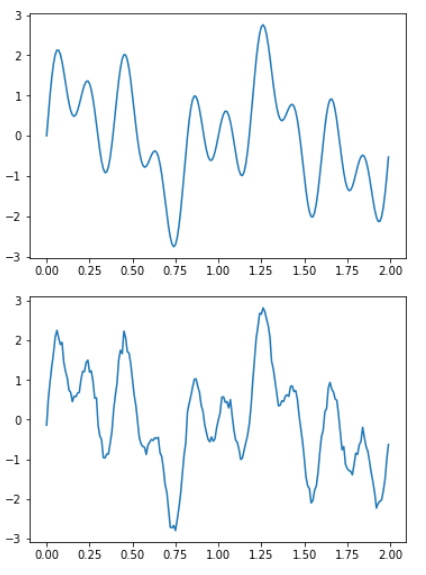
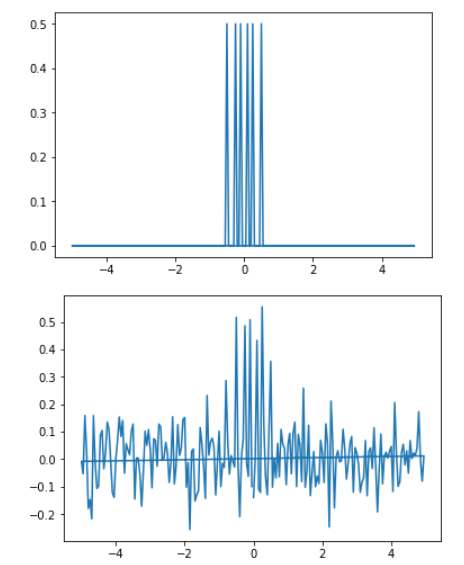
2.请生成y=sin(2pit)+sin(5pit)+sin(10pit)的时间信号,然后注入0.1倍的标准正态分布噪声数据,然后分别画出时间域的信号图,以及加入噪声前以及加入噪声后的FFT傅里叶变换后的频谱图。
Matplotlib实验(1)
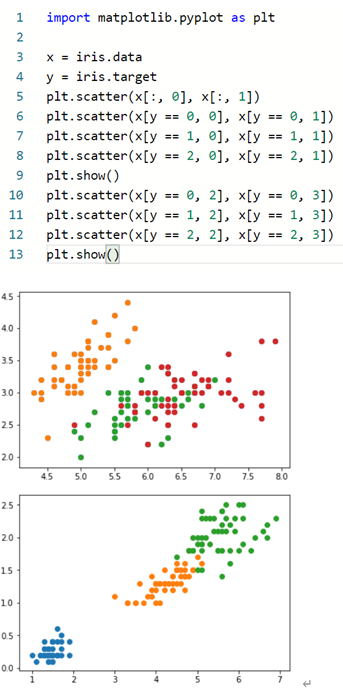
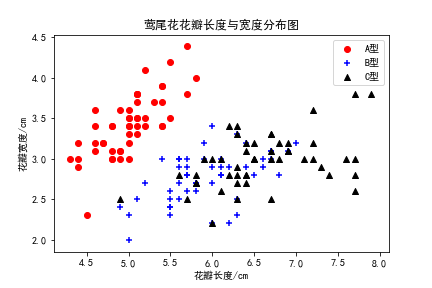
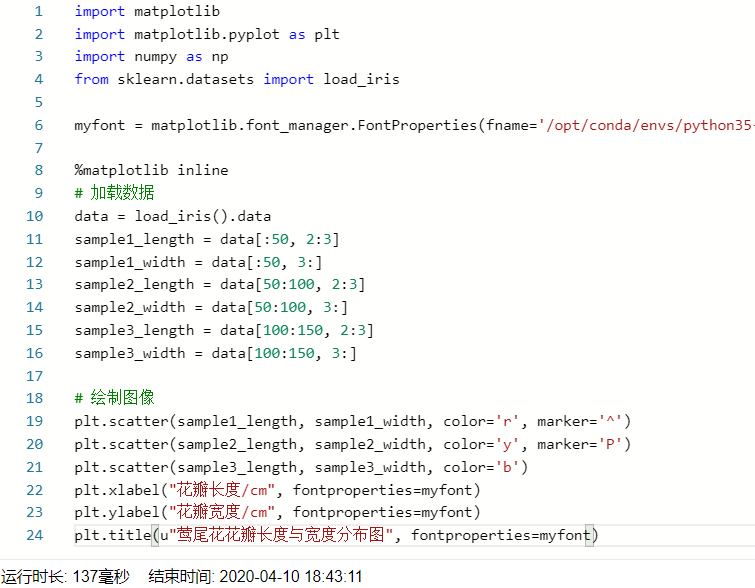
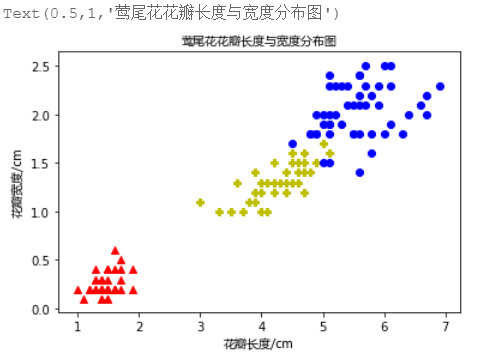
- 请加载sklearn的莺尾花数据,然后写代码画三种花瓣长和宽的散点分布图,绘制效果如下图所示。
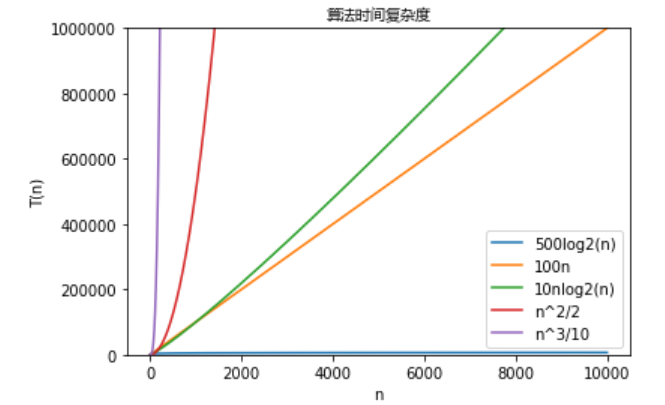
- 在数据结构中我们经常用到算法时间复杂度的概念,其中常用的几个算法时间复杂度如下所示:
O(1)<O(log2(n))<O(n)<O(nlog2(n))<O(n2)<O(n3)O(1)<O(log2(n))<O(n)<O(nlog2(n))<O(n^2)<O(n^3)O(1)<O(log2(n))<O(n)<O(nlog2(n))<O(n2)<O(n3)
现在有如下几个算法时间复杂度的函数,请绘制图像:n从1到1000
F(n)=500log2(n)F(n)=500log2(n)F(n)=500log2(n)
F(n)=100nF(n)=100nF(n)=100n
F(n)=10nlog2(n)F(n)=10nlog2(n)F(n)=10nlog2(n)
F(n)=n2/2F(n)=n^2/2F(n)=n2/2
F(n)=n3/10F(n)=n^3/10F(n)=n3/10
- 绘制折线图,将这些图绘制在一张图里面,注意要标注好每个线代表哪个复杂度函数,如果n不合适,可以继续增加或者减少,最好是能够体现时间复杂度的变化趋势来。

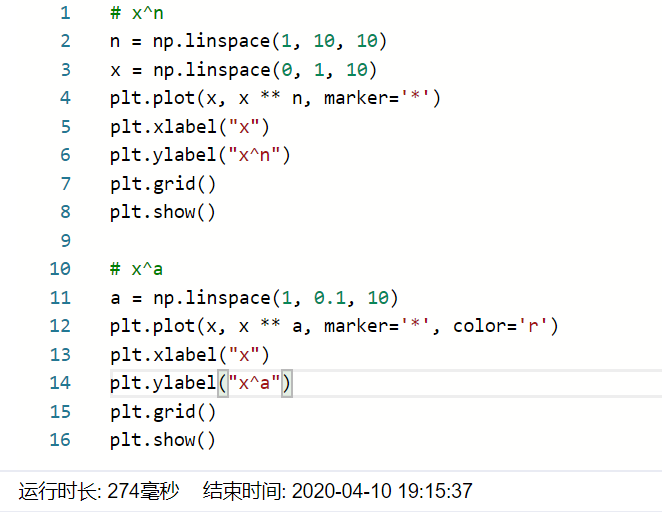
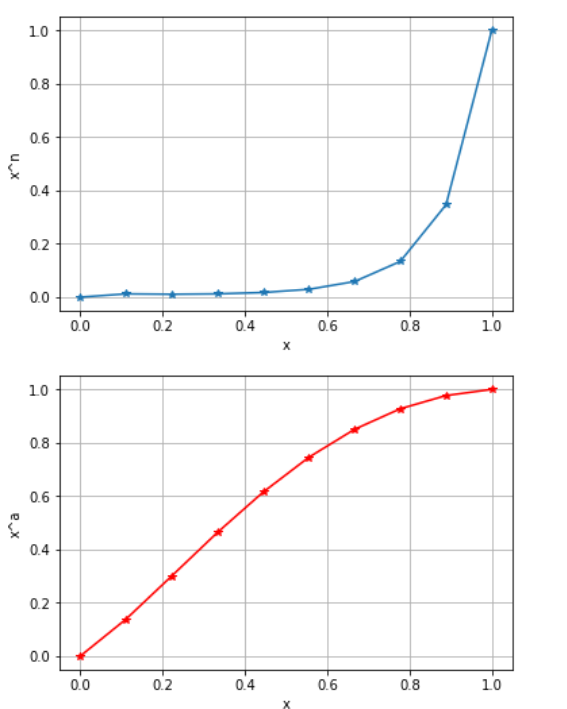
- 请绘制2张子图,第一张图上绘制xnx^nxn,n从1到10,x范围为0-1,第二张图上绘制xax^axa,a从1.0到0.1,x的范围还是0-1.
Matplotlib实验(2)
- 请加载sklearn的莺尾花数据,然后画柱状图、饼图和直方图
In [ ]
import numpy as np
import matplo相关文章:

Python实验代码合集
NumPy实验(1) NumPy实验(2) NumPy实验(3) SciPy实验(1) 请结合最小二乘法的原理,利用以前学的Numpy和Python知识,实现最小乘法直线拟合的算法,并测试。 请结合梯度下降的原理,利用以前学的Numpy和Python知识,实现梯度下降法求函数最小值的…...

Less和Sass的原理和用法
一、原理 1.1 Less定义:是一种动态的样式语言,使CSS变成一种动态的语言特性,如变量、继承、运算、函数。Less既可以在客户端上面运行(支持IE6以上版本、Webkit、Firefox),也可以在服务端运行(Node.js) 1.2 SaSS定义:是一种动态样式语言&#…...

c# List<T>.Aggregate
List<T>.Aggregate 方法的定义: public TAccumulate Aggregate<TAccumulate>(TAccumulate seed, Func<TAccumulate, T, TAccumulate> func)参数解析如下: TAccumulate seed:初始累积值,也是累积的起始值(默认…...
软件测试常用工具总结(测试管理、单元测试、接口测试、自动化测试、性能测试、负载测试等)
前言 在软件测试的过程中,多多少少都是会接触到一些测试工具,作为辅助测试用的,以提高测试工作的效率,使用好了测试工具,能对测试起到一个很好的作用,同时,有些公司,也会要求掌握一…...

Hadoop组件
前言 Hadoop 是一个能够对大量数据进行分布式处理的软件框架。具有可靠、高效、可伸缩的特点。 HDFS(hadoop分布式文件系统) 是hadoop体系中数据存储管理的基础。他是一个高度容错的系统,能检测和应对硬件故障。 Mapreduce(分…...
jeecg-boot批量导入问题注意事项
现象: 由于批量导入数据速度很快, 因为数据库中的create time字段的时间可能一样,并且jeecg框架自带的是根据生成时间排序, 因此在前端翻页查询的时候,数据每次排序可能会不一样, 会出现第一页已经出现过一…...

Django图书商城系统实战开发 - 实现会员管理
Django图书商城系统实战开发 - 实现会员管理 在Django图书商城系统中,会员管理是一个重要的功能模块。该模块包括会员信息的展示、编辑和删除等功能。以下是实现会员管理功能的详细步骤和代码示例。 步骤一:设计数据库模型 首先,我们需要设…...

Kafka如何解决消息丢失的问题
在 Kafka 的整个架构中可以总结出消息有三次传递的过程: Producer 端发送消息给 Broker 端Broker 将消息进行并持久化数据Consumer 端从 Broker 将消息拉取并进行消费 在以上这三步中每一步都可能会出现丢失数据的情况, 那么 Kafka 到底在什么情况下才…...

我只记得512天在CSDN的日子
机缘 不知不觉开始写博客已经512天了,在这期间有过因为懒惰想要放弃,也有过写不出优质文章没有阅读量的气馁,也有过学习蛮久却不知道从何开始写起的迷茫,但是最终好在还是坚持了下来,无论好坏坚持总没有错。 写博客的…...

pycharm,VSCode 几个好用的插件
pycharm Tabnine AI Code 可以在编写程序的时候为你提供一些快捷方式,增加编程速度 Chinese 对英文不好的程序员来说是个不错的选择,可以将英文状态下的pycharm变为中文版的 ChatGPT 可以跟ai聊天,ai可以解决你80%的问题 ,也可以帮…...

springboot 使用zookeeper实现分布式ID
添加ZooKeeper依赖:在pom.xml文件中添加ZooKeeper客户端的依赖项。例如,可以使用Apache Curator作为ZooKeeper客户端库: <dependency><groupId>org.apache.curator</groupId><artifactId>curator-framework</arti…...

git cherry-pick
cherry-pick命令的基本用法 对于多分支的代码库,将代码从一个分支转移到另一个分支是常见需求。这时分两种情况。一种情况是,你需要另一个分支的所有代码变动,那么就采用合并( git merge )。另一种情况是,…...
转行软件测试四个月学习,第一次面试经过分享
我是去年上半年从销售行业转行到测试的,从销售公司辞职之后选择去培训班培训软件测试,经历了四个月左右的培训,在培训班结课前两周就开始投简历了,在结课的时候顺利拿到了offer。在新的公司从事软件测试工作已经将近半年有余&…...

ECS服务器安装docker
为了安装并配置 Docker ,你的系统必须满足下列最低要求: 64 位 Linux 或 Windows 系统 如果使用 Linux ,内核版本必须不低于 3.10 能够使用 sudo 权限的用户 在你系统 BIOS 上启用了 VT(虚拟化技术)支持 on your s…...

高等数学教材啃书汇总重难点(三)微分中值定理与导数的应用
本章节包含多个知识点,一些列微分中值定理是考研证明题的重头戏,而洛必达和泰勒展开则是方法论的天花板难度,虽然对于小题的考察难度较低,整体上仍需重点复习 1.费马引理 2.罗尔定理 3.拉格朗日定理 4.柯西中值定理 5.洛必达法则 …...

域名列表是什么?
域名列表指的是一个网站上所使用的所有域名地址。在互联网发展的今天,拥有一个有效的域名列表对于一个企业或组织来说是非常重要的。本文将围绕着域名列表这一主题展开,并从以下几个方面进行分析。 一、为什么需要域名列表? 首先࿰…...

数据库操作不再困难,MyBatis动态Sql标签解析
系列文章目录 MyBatis缓存原理 Mybatis的CachingExecutor与二级缓存 Mybatis plugin 的使用及原理 MyBatis四大组件Executor、StatementHandler、ParameterHandler、ResultSetHandler 详解 MyBatisSpringboot 启动到SQL执行全流程 数据库操作不再困难,MyBatis动态S…...

Android 网络编程-网络请求
Android 网络编程-网络请求 文章目录 Android 网络编程-网络请求一、主要内容二、开发网络请求前的基本准备1、查看需要请求的网址是否有效(1)通过网页在线验证(2)使用专用window网咯请求工具(3)编写app代码…...

Mac下全选,使用pynput,怎样调用command键?
Key.command 不行,用Key.cmd 。 win或linux下: with keyboard.pressed(Key.ctrl):keyboard.press(a)time.sleep(1)keyboard.release(a) 那么在mac下就是: with keyboard.pressed(Key.cmd):keyboard.press(a)time.sleep(1)keyboard.rel…...
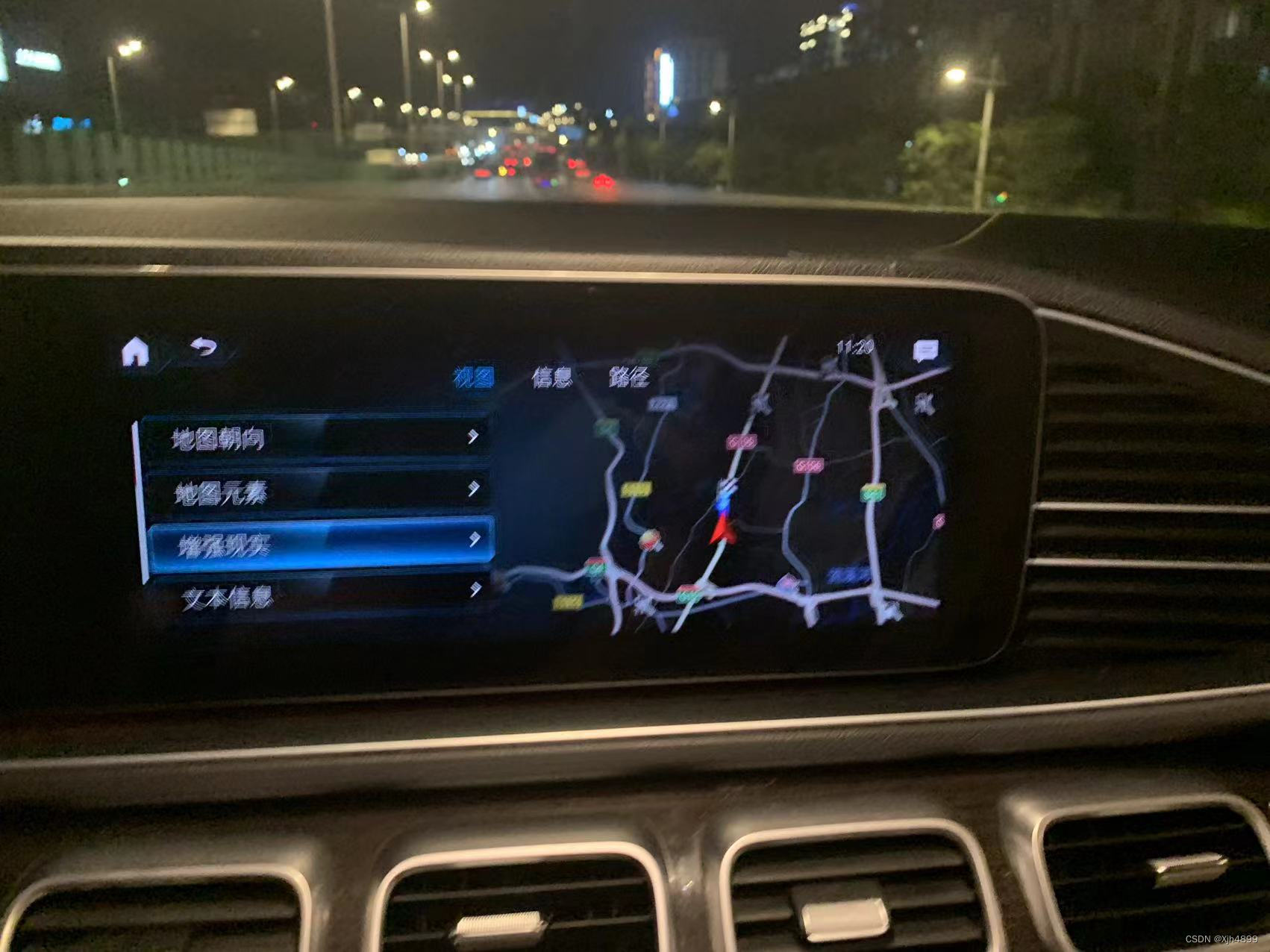
21款美规奔驰GLS450更换中规高配主机,汉化操作更简单
很多平行进口的奔驰GLS都有这么一个问题,原车的地图在国内定位不了,语音交互功能也识别不了中文,原厂记录仪也减少了,使用起来也是很不方便的。 可以实现以下功能: ①中国地图 ②语音小助手(你好…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
