数据结构——堆
数据结构——堆
- 堆
- 堆简介
- 堆的分类
- 二叉堆
- 过程
- 插入操作
- 删除操作
- 向下调整:
- 增加某个点的权值
- 实现
- 参考代码:
- 建堆
- 方法一:使用 decreasekey(即,向上调整)
- 方法二:使用向下调整
- 应用
- 对顶堆
- 其他:
- 配对堆:
- 左偏树:
堆
堆简介
堆是一棵树,其每个节点都有一个键值,且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆,否则叫做大根堆。STL 中的 priority_queue 其实就是一个大根堆。
(小根)堆主要支持的操作有:插入一个数、查询最小值、删除最小值、合并两个堆、减小一个元素的值。
一些功能强大的堆(可并堆)还能(高效地)支持 merge 等操作。
一些功能更强大的堆还支持可持久化,也就是对任意历史版本进行查询或者操作,产生新的版本。
堆的分类

习惯上,不加限定提到「堆」时往往都指二叉堆。
二叉堆
结构
从二叉堆的结构说起,它是一棵二叉树,并且是完全二叉树,每个结点中存有一个元素(或者说,有个权值)。
堆性质:父亲的权值不小于儿子的权值(大根堆)。同样的,我们可以定义小根堆。本文以大根堆为例。
由堆性质,树根存的是最大值(getmax 操作就解决了)。
过程
插入操作
插入操作是指向二叉堆中插入一个元素,要保证插入后也是一棵完全二叉树。
最简单的方法就是,最下一层最右边的叶子之后插入。
如果最下一层已满,就新增一层。
插入之后可能会不满足堆性质?
向上调整:如果这个结点的权值大于它父亲的权值,就交换,重复此过程直到不满足或者到根。
可以证明,插入之后向上调整后,没有其他结点会不满足堆性质。
向上调整的时间复杂度是 O ( l o g n ) O(log n) O(logn)的。
删除操作
删除操作指删除堆中最大的元素,即删除根结点。
但是如果直接删除,则变成了两个堆,难以处理。
所以不妨考虑插入操作的逆过程,设法将根结点移到最后一个结点,然后直接删掉。
然而实际上不好做,我们通常采用的方法是,把根结点和最后一个结点直接交换。
于是直接删掉(在最后一个结点处的)根结点,但是新的根结点可能不满足堆性质……
向下调整:
在该结点的儿子中,找一个最大的,与该结点交换,重复此过程直到底层。
可以证明,删除并向下调整后,没有其他结点不满足堆性质。
时间复杂度 O ( l o g n ) O(log n) O(logn)。
增加某个点的权值
很显然,直接修改后,向上调整一次即可,时间复杂度为 O ( l o g n ) O(log n) O(logn)。
实现
我们发现,上面介绍的几种操作主要依赖于两个核心:向上调整和向下调整。
考虑使用一个序列 h h h 来表示堆。 h i h_i hi 的两个儿子分别是 h 2 h_2 h2 i _i i 和 h 2 h_2 h2 i _i i + _+ + 1 _1 1, 1 1 1 是根结点:
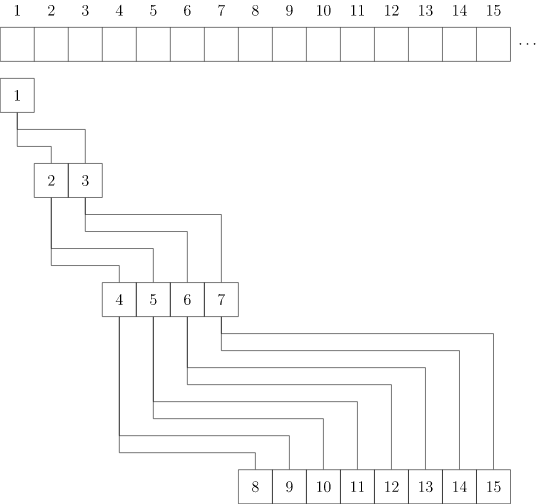
参考代码:
void up(int x) {while (x > 1 && h[x] > h[x / 2]) {swap(h[x], h[x / 2]);x /= 2;}
}void down(int x) {while (x * 2 <= n) {t = x * 2;if (t + 1 <= n && h[t + 1] > h[t]) t++;if (h[t] <= h[x]) break;std::swap(h[x], h[t]);x = t;}
}
建堆
考虑这么一个问题,从一个空的堆开始,插入 n 个元素,不在乎顺序。
直接一个一个插入需要 O ( n l o g n ) O(n log n) O(nlogn) 的时间,有没有更好的方法?
方法一:使用 decreasekey(即,向上调整)
从根开始,按 BFS 序进行。
void build_heap_1() {for (i = 1; i <= n; i++) up(i);
}
为啥这么做:对于第 k 层的结点,向上调整的复杂度为 O ( k ) O(k) O(k) 而不是 O ( l o g n ) O(log n) O(logn)。
总复杂度: l o g 1 log 1 log1 + l o g 2 log 2 log2 + … + l o g n log n logn = O ( n l o g n ) O(n log n) O(nlogn)。
(在「基于比较的排序」中证明过)
方法二:使用向下调整
这时换一种思路,从叶子开始,逐个向下调整
void build_heap_2() {for (i = n; i >= 1; i--) down(i);
}
换一种理解方法,每次「合并」两个已经调整好的堆,这说明了正确性。
注意到向下调整的复杂度,为 O ( l o g n − k ) O(log n - k) O(logn−k),另外注意到叶节点无需调整,因此可从序列约 n/2 的位置开始调整,可减少部分常数但不影响复杂度。
之所以能 O ( n ) O(n) O(n) 建堆,是因为堆性质很弱,二叉堆并不是唯一的。
要是像排序那样的强条件就难说了。
应用
对顶堆
这个问题可以被进一步抽象成:动态维护一个序列上第 k k k 大的数, k k k 值可能会发生变化。
对于此类问题,我们可以使用对顶堆这一技巧予以解决(可以避免写权值线段树或 B S T BST BST带来的繁琐)。
对顶堆由一个大根堆与一个小根堆组成,小根堆维护大值即前 k k k 大的值(包含第 k k k 个),大根堆维护小值即比第 k k k 大数小的其他数。
这两个堆构成的数据结构支持以下操作:
1.维护:当小根堆的大小小于 k k k 时,不断将大根堆堆顶元素取出并插入小根堆,直到小根堆的大小等于 k k k;当小根堆的大小大于 k k k 时,不断将小根堆堆顶元素取出并插入大根堆,直到小根堆的大小等于 k k k;
2.插入元素:若插入的元素大于等于小根堆堆顶元素,则将其插入小根堆,否则将其插入大根堆,然后维护对顶堆;
3.查询第 k 大元素:小根堆堆顶元素即为所求;
4.删除第 k 大元素:删除小根堆堆顶元素,然后维护对顶堆;
显然,查询第 k k k 大元素的时间复杂度是 O ( 1 ) O(1) O(1) 的。由于插入、删除或调整 k k k 值后,小根堆的大小与期望的 k k k 值最多相差 1 1 1,故每次维护最多只需对大根堆与小根堆中的元素进行一次调整,因此,这些操作的时间复杂度都是 O ( l o g n ) O(log n) O(logn) 的。
其他:
配对堆:
详见:链接: 数据结构——配对堆
左偏树:
详见后文。
相关文章:

数据结构——堆
数据结构——堆 堆堆简介堆的分类 二叉堆过程插入操作 删除操作向下调整: 增加某个点的权值实现参考代码:建堆方法一:使用 decreasekey(即,向上调整)方法二:使用向下调整 应用对顶堆 其他&#…...

重复学习1:NLP
目录 1. 自然语言处理与知识图谱1.1 RNN 循环神经网络初探 2. 吴恩达深度学习 1. 自然语言处理与知识图谱 1.1 RNN 循环神经网络初探 1.1.2 回顾数据维度与神经网络(1) 2. 吴恩达深度学习 P151 1.1 为什么选择序列模型(1,2) P152 1.2 数学符号(1,)...
做海外游戏推广有哪些条件?
做海外游戏推广需要充分准备和一系列条件的支持。以下是一些关键条件: 市场调研和策略制定:了解目标市场的文化、玩家偏好、竞争格局等是必要的。根据调研结果制定适合的推广策略。 本地化:将游戏内容、界面、语言、货币等进行本地化&#…...
JavaFx基础学习【五】:FXML布局文件使用
目录 前言 一、介绍 二、简单体验 三、FXML标签元素 四、fx属性介绍 五、重写initialize(名字需要保持一致)方法 六、Scene Builder快速布局 前言 如果你还没有看过前面的文章,可以通过以下链接快速前往学习: JavaFx基础学…...

通过Python爬虫提升网站搜索排名
目录 怎么使用Python爬虫提升排名 1. 抓取竞争对手数据: 2. 关键词研究: 3. 网页内容优化: 4. 内部链接建设: 5. 外部链接建设: 6. 监测和调整: 需要注意哪些方面 1. 合法性和道德性: …...

【博客698】为什么当linux作为router使用时,安装docker后流量转发失败
为什么当linux作为router使用时,安装docker后流量转发失败 场景 当一台linux机器作为其它服务器的router,负责转发流量的时候,让你在linux上安装docker之后,就会出现流量都被drop掉了 原因 没装docker之前: [root~]…...
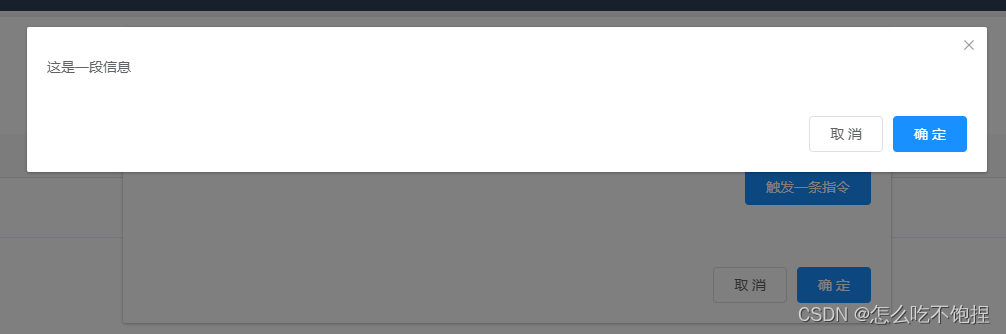
el-dialog嵌套,修改内层el-dialog样式(自定义样式)
el-dialog嵌套使用时,内层的el-dialog要添加append-to-body属性 给内层的el-dialog添加custom-class属性,添加自定义类名 <el-dialog:visible.sync"dialogVisible"append-to-bodycustom-class"tree-cesium-container"><span>这是一段信息<…...
B树和B+树区别
B树和B树的区别 B树 B树被称为平衡树,在B树中,一个节点可以有两个以上的子节点。B树的高度为log M N。在B树中,数据按照特定的顺序排序,最小值在左侧,最大值在右侧。 B树是一种平衡的多分树,通常我们说m阶…...
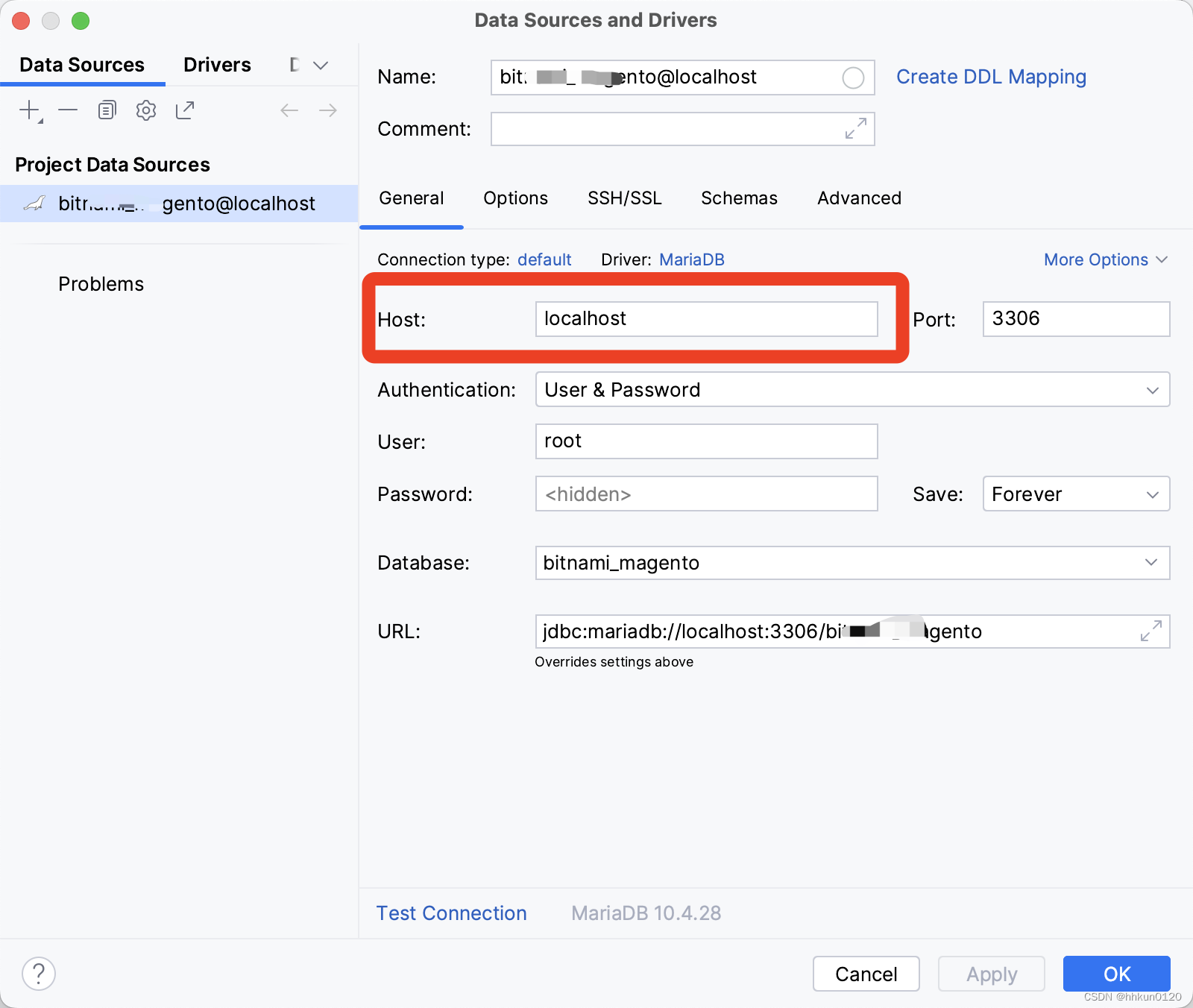
intelJ IDEA\PHPStorm \WebStorm\PyCharm 通过ssh连接远程Mysql\Postgresql等数据库
最容易出错的地方是在general面板下的host,不应该填真实的host地址,而应该填localhost或者127.0.0.1 具体操作步骤见下图...

vfuhyuuy
Sublime Text is an awesome text editor. If you’ve never heard of it, you shouldcheck it out right now. I’ve made this tutorial because there’s no installer for the Linux versions of Sublime Text. While that’s not a real problem, I feel there is a clean…...

CSS自学框架之表单
首先我们看一下表单样式,下面共有5张截图 一、CSS代码 /*表单*/fieldset{border: none;margin-bottom: 2em;}fieldset > *{ margin-bottom: 1em }fieldset:last-child{ margin-bottom: 0 }fieldset legend{ margin: 0 0 1em }/* legend标签是CSS中用于定义…...

使用Spring Boot和Redis实现用户IP接口限流的详细指南
系列文章目录 文章目录 系列文章目录前言一、准备工作二、编写限流过滤器三、配置Redis四、测试接口限流总结 前言 在高并发场景下,为了保护系统免受恶意请求的影响,接口限流是一项重要的安全措施。本文将介绍如何使用Spring Boot和Redis来实现用户IP的…...
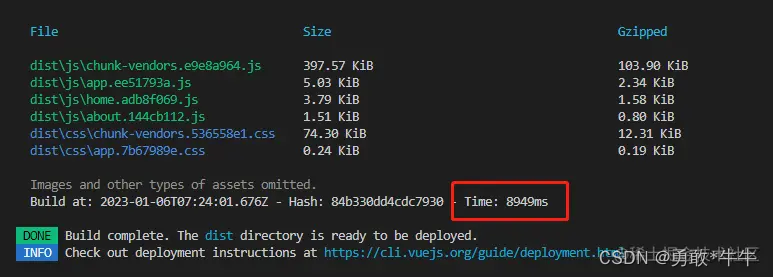
前端性能优化——包体积压缩插件,打包速度提升插件,提升浏览器响应的速率模式
前端代码优化 –其他的优化可以具体在网上搜索 压缩项目打包后的体积大小、提升打包速度,是前端性能优化中非常重要的环节,结合工作中的实践总结,梳理出一些 常规且有效 的性能优化建议 ue 项目可以通过添加–report命令: "…...
配置vscode
配置vscode 设置相关 网址:https://code.visualstudio.com/ 搜索不要用百度用这个:cn.bing.com 1.安装中文包 Chinese (Simplified) (简体中文) 2.安装 open in browser 3.安装主题 Atom One Dark Theme 4. 安装图标样式 VSCode Great Icons 5.安装 L…...
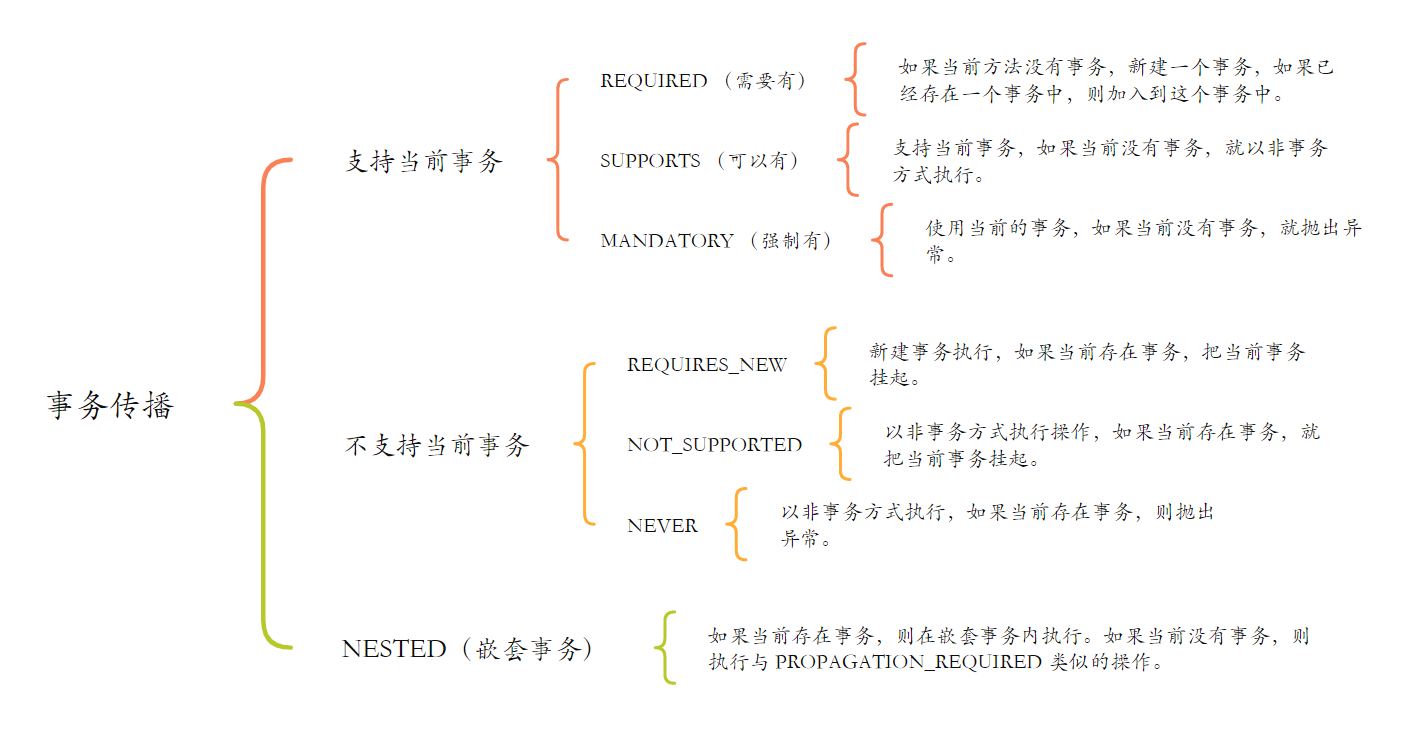
【Spring】深入理解 Spring 事务及其传播机制
文章目录 一、Spring 事务是什么二、Spring 中事务的实现方法2.1 Spring 编程式事务(手动)2.1.1 编程式事务的使用演示2.1.2 编程式事务存在的问题 2.2 Spring 声明式事务(自动)2.2.1 Transactional 作用范围2.2.2 Transactional …...

eclipse常用设置
1、调整编辑页面字体大小 窗口 (Window)- 首选项(Preferences)- 常规(General)- 外观 (Appearence)- 颜色与字体 (Colors And Fonts),在右边的对话框里选择 Java - Java Editor Text Font,点击出现的修改&…...

ajax解析
Ajax(Asynchronous JavaScript and XML)是一种用于在不重新加载整个页面的情况下与服务器交换数据的技术。它通过异步的方式发送请求和接收响应,能够实现在后台与服务器进行数据交互,然后更新页面的部分内容,从而提升用…...

CSS3:图片边框
简介 图片也可以作为边框,以下是实例演示 注意 实现该效果必须添加border样式,且必须位于border-image-socure之前否则不会生效 实例 <html lang"en"><head><style>p {width: 600px;margin: 200px auto;border: 30px soli…...
(七)Unity VR项目升级至Vision Pro需要做的工作
Vision Pro 概述 定位为混合现实眼镜,对AR支持更友好 无手柄,支持手(手势)、眼(注视)、语音交互 支持空间音频,相比立体声、环绕声更有沉浸感和空间感 支持VR/AR应用,支持多种应用模…...
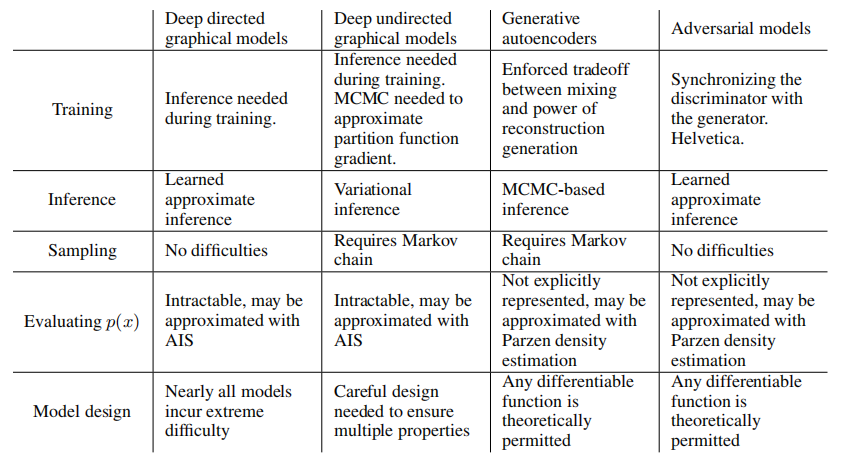
【计算机视觉|生成对抗】生成对抗网络(GAN)
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Generative Adversarial Nets 链接:Generative Adversarial Nets (nips.cc) 摘要 我们提出了一个通过**对抗(adversarial)**过程估计生成模型的新框架…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用
Linux 内存管理调试分析:ftrace、perf、crash 的系统化使用 Linux 内核内存管理是构成整个内核性能和系统稳定性的基础,但这一子系统结构复杂,常常有设置失败、性能展示不良、OOM 杀进程等问题。要分析这些问题,需要一套工具化、…...
