周期 角频率 频率 振幅 初相角
周期 角频率 频率 振幅 初相角
当我们谈论傅里叶级数或波形分析时,以下术语经常出现:
-
周期 T T T: 函数在其图形上重复的时间或空间的长度。周期的倒数是频率。
-
频率 f f f: 周期的倒数,即一秒内波形重复的次数。单位通常为赫兹(Hz)。
f = 1 T f = \frac{1}{T} f=T1 -
角频率 ω \omega ω: 角频率是频率的 2 π 2\pi 2π倍,通常用于正弦和余弦函数中。
ω = 2 π f = 2 π T \omega = 2\pi f = \frac{2\pi}{T} ω=2πf=T2π -
振幅: 振幅是波形的最大幅度或强度。在傅里叶级数中,振幅由正弦和余弦项的系数确定,可以反映波形的大小。
-
初相角 ϕ \phi ϕ: 初始相位或相位偏移表示波形在时间 t = 0 t = 0 t=0时的位置。在正弦和余弦波中,相位偏移可以将波形沿时间轴移动。
将这些概念结合起来,可以得到一个周期函数的一般形式:
f ( t ) = A cos ( ω t + ϕ ) f(t) = A \cos(\omega t + \phi) f(t)=Acos(ωt+ϕ)
其中:
- A A A 是振幅
- ω \omega ω 是角频率
- t t t 是时间
- ϕ \phi ϕ 是初相角
这些参数共同决定了波形的外观和特性。在傅里叶分析中,它们帮助我们将复杂的波形分解为简单的正弦和余弦波的组合。
当然!让我们通过一个具体的例子来解释这些概念。
假设我们有一个信号,其表达式为:
f ( t ) = 3 cos ( 2 π ⋅ 2 t + π 3 ) f(t) = 3 \cos(2\pi \cdot 2t + \frac{\pi}{3}) f(t)=3cos(2π⋅2t+3π)
我们可以从这个公式中识别以下参数:
-
振幅 A = 3 A = 3 A=3: 这告诉我们该信号的最大幅度为3。
-
角频率 ω = 2 π ⋅ 2 \omega = 2\pi \cdot 2 ω=2π⋅2: 这告诉我们该信号每秒会完成 2 ⋅ 2 π 2 \cdot 2\pi 2⋅2π 弧度的振动。
-
频率 f = 2 f = 2 f=2: 由角频率除以 2 π 2\pi 2π 得到,这告诉我们该信号每秒振动2次,即周期为0.5秒。
-
周期 f = 1 T f = \frac{1}{T} f=T1: 给定频率 f = 2 f = 2 f=2,我们可以解得: T = 1 2 秒 T = \frac{1}{2} \text{ 秒} T=21 秒,所以这个信号的周期是0.5秒,意味着每0.5秒信号的波形会重复一次。
-
初相角 ϕ = π 3 \phi = \frac{\pi}{3} ϕ=3π: 这反映了波形在 t = 0 t = 0 t=0时的位置,或者说该波形相对于标准余弦波的偏移。
这个特定的信号可以描述许多不同的物理系统,从简单的弹簧振荡器到交流电流。振幅、频率和相位的这些参数提供了描述波形特性的完整信息。
在傅里叶分析中,这样的波形可以被看作是一个更复杂信号的构成部分。通过将复杂信号分解为这样的简单正弦和余弦波,我们可以更容易地理解和分析它。
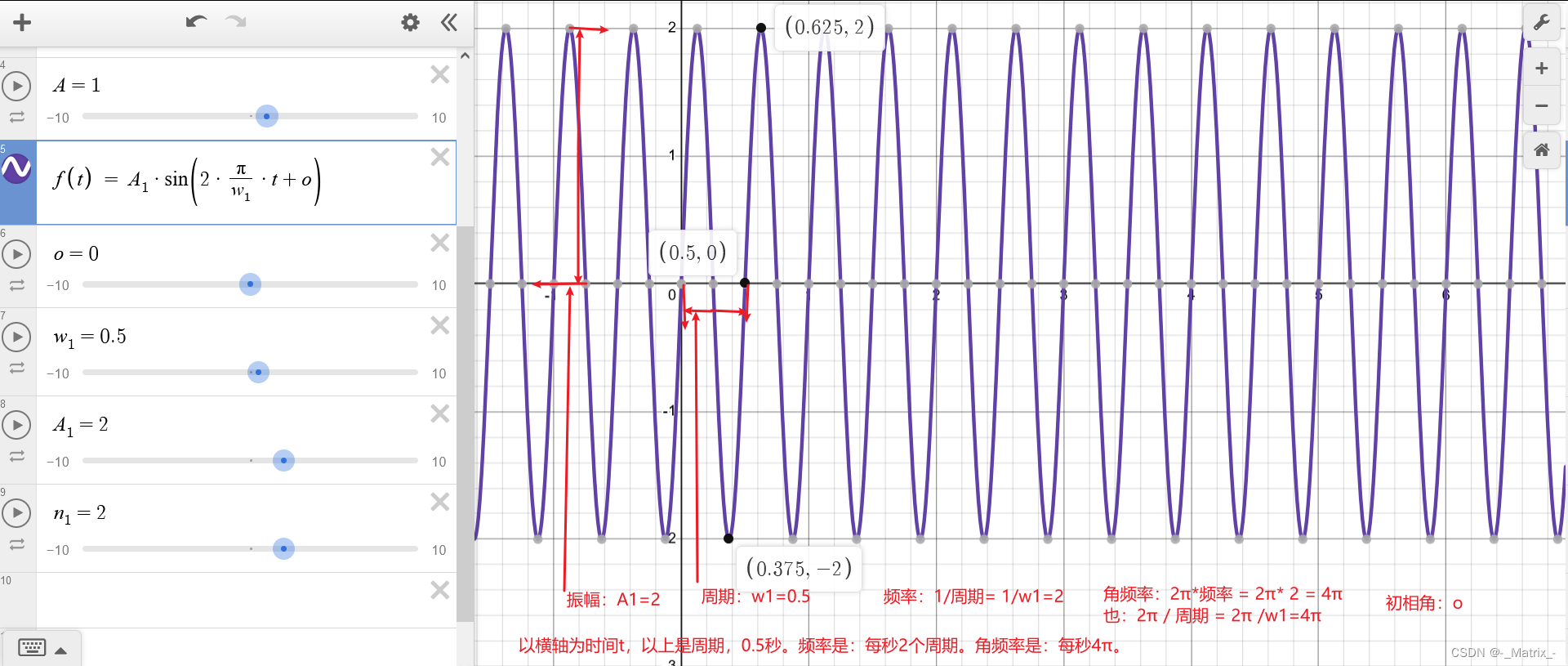
相位差
相位差是描述两个或多个周期信号之间相对时间偏移的量度。对于两个相同频率的正弦波信号,相位差可以表达为它们的峰值在时间上的偏移量。
用数学表示,假设有两个正弦波信号:
A 1 sin ( 2 π f t + ϕ 1 ) A_1 \sin(2\pi f t + \phi_1) A1sin(2πft+ϕ1)
A 2 sin ( 2 π f t + ϕ 2 ) A_2 \sin(2\pi f t + \phi_2) A2sin(2πft+ϕ2)
其中, A 1 A_1 A1 和 A 2 A_2 A2 是振幅, f f f是频率, t t t 是时间,而 ϕ 1 \phi_1 ϕ1 和 ϕ 2 \phi_2 ϕ2是初始相位。
这两个信号的相位差就是 ϕ 2 − ϕ 1 \phi_2 - \phi_1 ϕ2−ϕ1,可以用弧度或度来表示。
相位差对于许多工程和物理应用都很重要,例如在通信、声学和电力系统中。不同的相位差可能会导致系统行为的显著不同。例如,在交流电路中,电流和电压之间的相位差与电路中的功率因素有关;在通信系统中,相位差可以用于编码信息等。
相关文章:

周期 角频率 频率 振幅 初相角
周期 角频率 频率 振幅 初相角 当我们谈论傅里叶级数或波形分析时,以下术语经常出现: 周期 T T T: 函数在其图形上重复的时间或空间的长度。周期的倒数是频率。 频率 f f f: 周期的倒数,即一秒内波形重复的次数。单位通常为赫兹ÿ…...

根据一棵树的两种遍历构造二叉树
题目 给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 示例 1: 输入: preorder [3,9,20,15,7], inorder [9,3,15,20,7] 输出: [3,9,20,null,null,…...
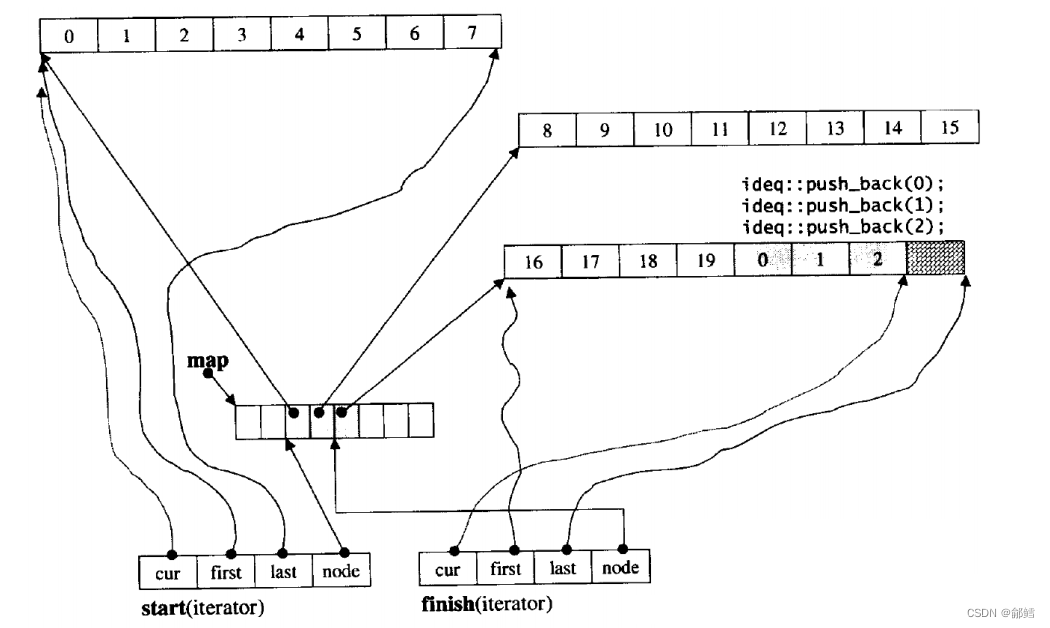
stack 、 queue的语法使用及底层实现以及deque的介绍【C++】
文章目录 stack的使用queue的使用适配器queue的模拟实现stack的模拟实现deque stack的使用 stack是一种容器适配器,具有后进先出,只能从容器的一端进行元素的插入与提取操作 #include <iostream> #include <vector> #include <stack&g…...

没学C++,如何从C语言丝滑过度到python【python基础万字详解】
大家好,我是纪宁。 文章将从C语言出发,深入介绍python的基础知识,也包括很多python的新增知识点详解。 文章目录 1.python的输入输出,重新认识 hello world,重回那个激情燃烧的岁月1.1 输出函数print的规则1.2 输入函…...

haproxy负载均衡
1、配置环境 作用环境windows测试 192.168.33.158 172.25.0.11 haproxy负载均衡haproxy:2.8.1,centos7172.25.0.31web服务器1--rs1Apache:2.4,redhat9172.25.0.32web服务器2--rs2Apache:2.4 , redhat9 2、…...
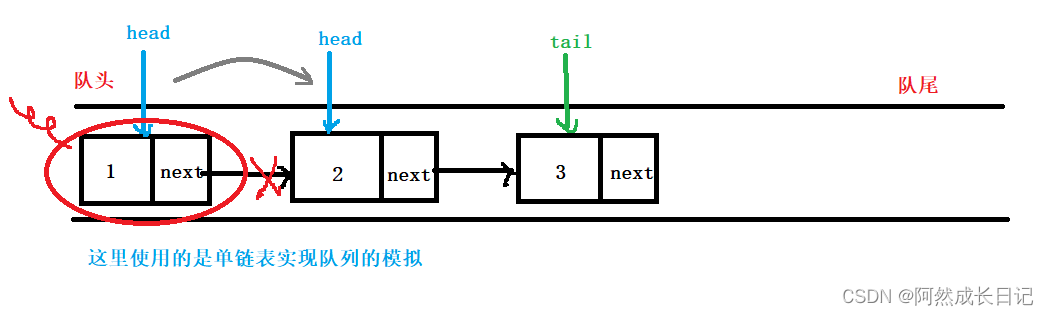
【数据结构】顺序队列模拟实现
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
TiDB数据库从入门到精通系列之六:使用 TiCDC 将 TiDB 的数据同步到 Apache Kafka
TiDB数据库从入门到精通系列之六:使用 TiCDC 将 TiDB 的数据同步到 Apache Kafka 一、技术流程二、搭建环境三、创建Kafka changefeed四、写入数据以产生变更日志五、配置 Flink 消费 Kafka 数据 一、技术流程 快速搭建 TiCDC 集群、Kafka 集群和 Flink 集群创建 c…...
Spring对象装配
在spring中,Bean的执行流程为启动spring容器,实例化bean,将bean注册到spring容器中,将bean装配到需要的类中。 既然我们需要将bea装配到需要的类中,那么如何实现呢?这篇文章,将来阐述一下如何实…...
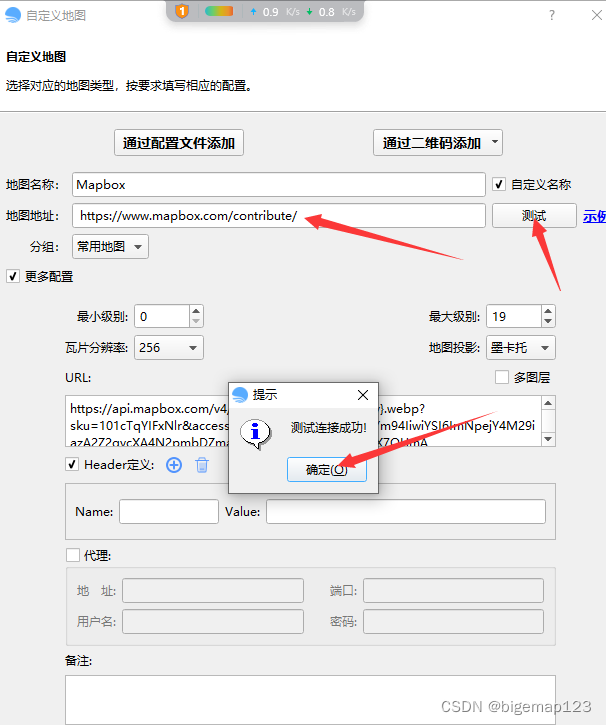
bigemap如何添加mapbox地图?
第一步 打开浏览器,找到你要访问的地图的URL地址,并且确认可以正常在浏览器中访问;浏览器中不能访问,同样也不能在软件中访问。 以下为常用地图源地址: 天地图: http://map.tianditu.gov.cn 包含&…...

python爬虫6:lxml库
python爬虫6:lxml库 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生不好…...

Linux查找命令
find find /dir -name filename 按名字查找 find . -name “*.c” 将当前目录及其子目录下所有文件后缀为 .c 的文件列出来 find . -type f 将当前目录及其子目录中的所有文件列出 find . -ctime 20 将当前目录及其子目录下所有最近 20 天内更新过的文件列出 find / -type f -…...
在 IntelliJ IDEA 中使用 Docker 开发指南
目录 一、IDEA安装Docker插件 二、IDEA连接Docker 1、Docker for Windows 连接 2、SSH 连接 3、Connection successful 连接成功 三、查看Docker面板 四、使用插件生成镜像 一、IDEA安装Docker插件 打开 IntelliJ IDEA,点击菜单栏中的 "File" -&g…...

【并发编程】自研数据同步工具的优化:创建线程池多线程异步去分页调用其他服务接口获取海量数据
文章目录 场景:解决方案 场景: 前段时间在做一个数据同步工具,其中一个服务的任务是调用A服务的接口,将数据库中指定数据请求过来,交给kafka去判断哪些数据是需要新增,哪些数据是需要修改的。 刚开始的设…...
)
python函数、运算符等简单介绍3(无顺序)
set(集合) 集合(set) -> 负责存储【不重复的数据】,并且是【无序存储】 的容器,主要用来去重和逻辑比较 set1 {1,2,3,4,58,7,4,1,2,3,5} print(set1) print(type(set1)) # 输出结果: {1, 2, 3, 4, 5, 7, 58} <…...
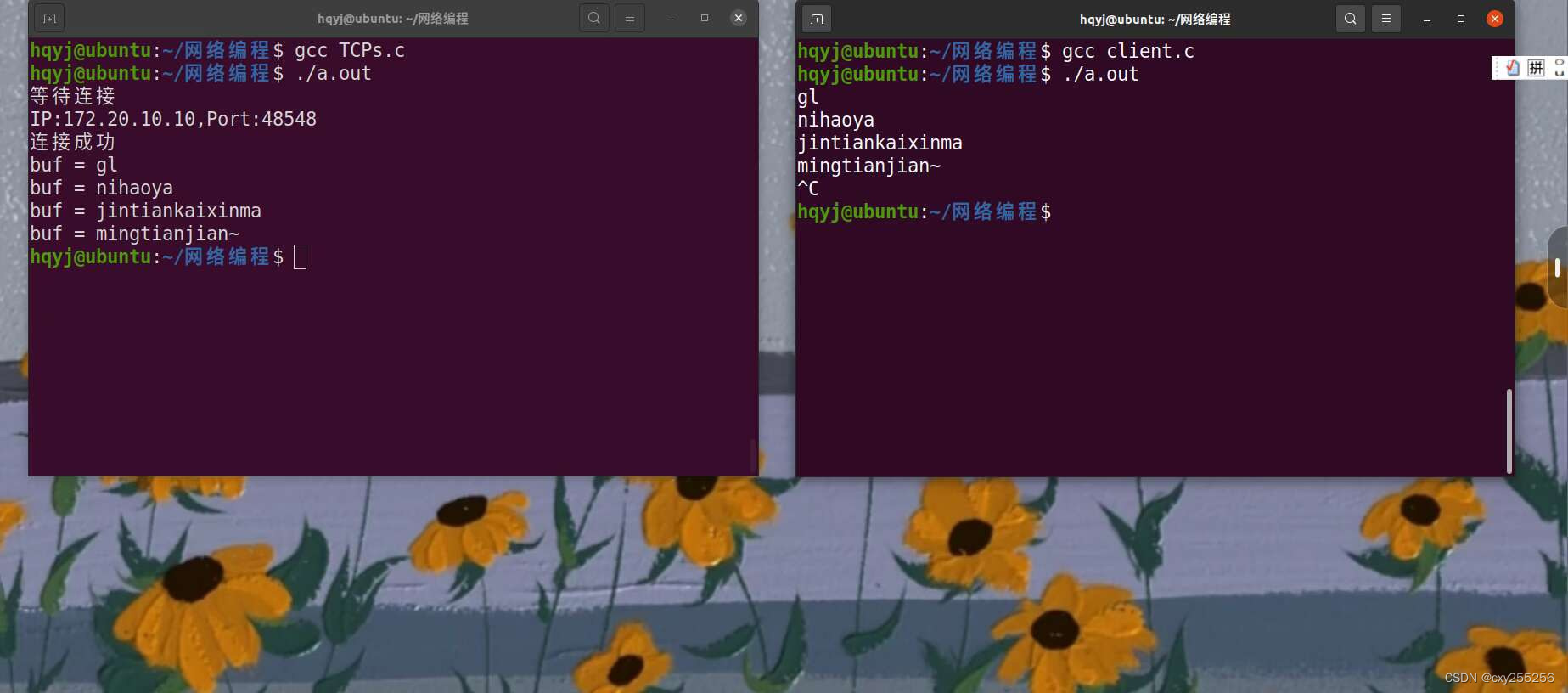
TCP服务器(套接字通信)
服务器 客户端 结果...
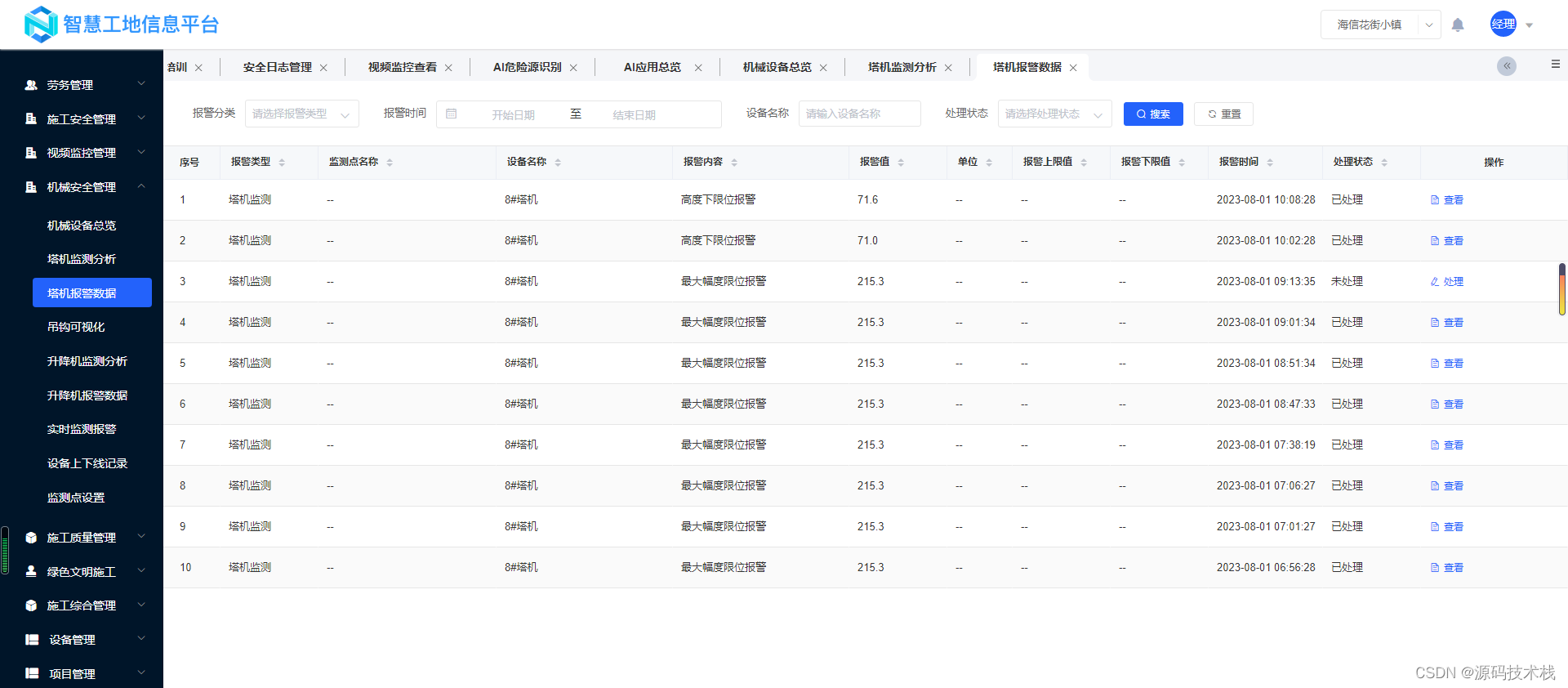
【智慧工地源码】:人工智能、BIM技术、机器学习在智慧工地的应用
智慧工地云平台是专为建筑施工领域所打造的一体化信息管理平台。通过大数据、云计算、人工智能、BIM、物联网和移动互联网等高科技技术手段,将施工区域各系统数据汇总,建立可视化数字工地。同时,围绕人、机、料、法、环等各方面关键因素&…...
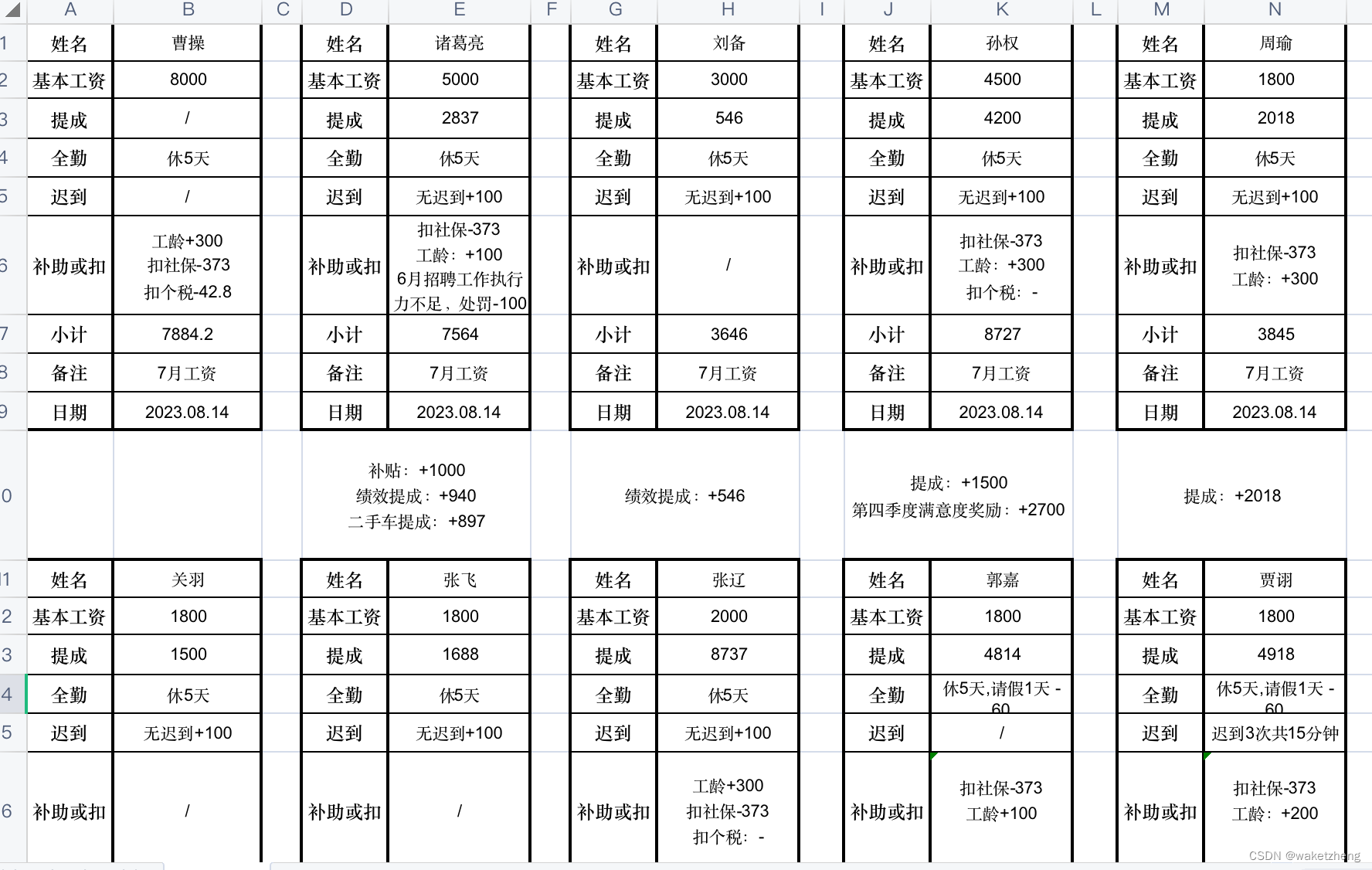
使用python读Excel文件并写入另一个xls模版
效果如下: 原文件内容 转化后的内容 大致代码如下: 1. load_it.py #!/usr/bin/env python import re from datetime import datetime from io import BytesIO from pathlib import Path from typing import List, Unionfrom fastapi import HTTPExcep…...

债务人去世,债权人要求其妻女承担还款责任,法院支持吗
债务人去世,债权人要求其妻女承担还款责任,法院支持吗 2019年9月20日,老张以公司资金周转为由向好友任某先后借款合计40万。2022年8月27日老张出具还款承诺书,承诺2022年11月30日前归还本息(本息90万元)到…...
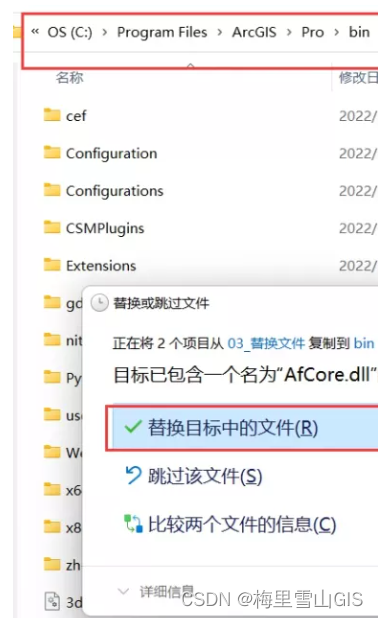
arcgis pro3.0-3.0.1-3.0.2安装教程大全及安装包下载
一. 产品介绍: ArcGIS Pro 这一功能强大的单桌面 GIS 应用程序是一款功能丰富的软件,采用 ArcGIS Pro 用户社区提供的增强功能和创意进行开发。 ArcGIS Pro 支持 2D、3D 和 4D 模式下的数据可视化、高级分析和权威数据维护。 支持通过 Web GIS 在一系列 …...
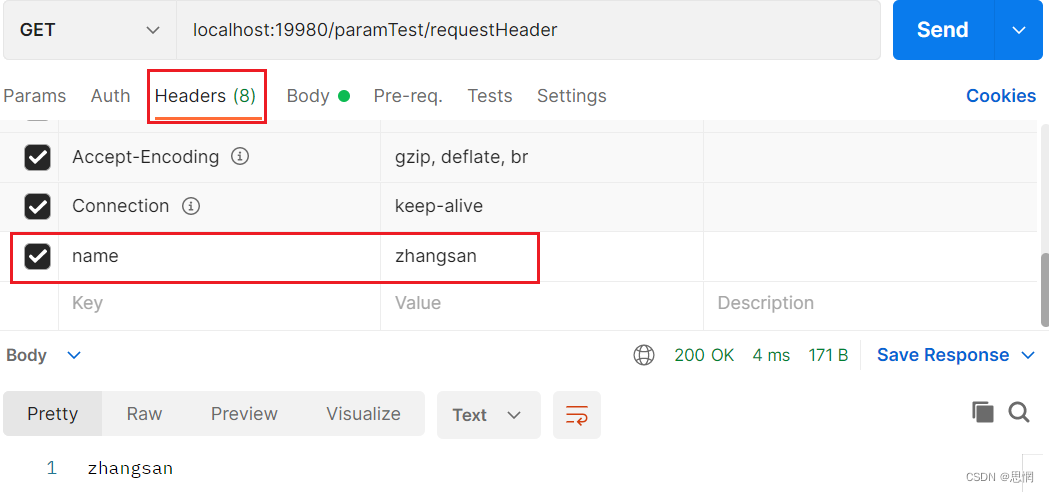
@RequestHeader使用
RequestHeader 请求头参数的设置 GetMapping("paramTest/requestHeader")public String requestHeaderTest(RequestHeader("name") String name){return name;} 在Postman的Headers中添加请求头参数,不过貌似不能加中文...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
