当前位置： 首页 > news >正文

数学建模-多元线性回归笔记

news 文章来源：https://blog.csdn.net/qq_61735602/article/details/132332346 2025/5/23 17:15:05

数学建模笔记

1.学模型✅
2.看专题论文并复习算法

  • 多元线性回归

    • 无偏性：预测值与真实值非常接近
    • 一致性：样本量无限增大，收敛于待估计参数的真值
    • 如何做：控制核心解释变量和u不相关

  • 四类模型回归系数的解释

    • 截距项不用考虑
    • 一元线性回归：y = a + bx + u
      • x每增加1个单位，y平均变化b个单位
    • 双对数模型：lny = a + blnx + u
      • x每增加1%，y平均变化b%
    • 半对数模型：y = a + blnx
      • x每增加1%，y平均变化b/100个单位
    • 半对数模型：lny = a + bx
      • x每增加1个单位，y平均变化(100b)%

  • 算回归系数要避免多重共线性

  • 客户对产品的关注度可以利用爬虫爬取评价量来表示

  • 多元线性回归 软件：STATA

    • 导入数据
    • 描述性统计：
      • 定量数据：summarize 评价量
        • 右键，复制表格
      • 定性数据：tabulate 变量名,<gen(A)>
        • 数据编辑器
    • 打开do文件，运行一部分
    • 回归数据说明
      • [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-weXrLv8R-1692215418652)(media/16921742285760/16921799343967.jpg)]

  • STATA回归

    • regress y x1 x2 … xk(默认用OLS：普通最小二乘法）
    • 加入虚拟变量(定类变量)
      • regress y x1 G1 G2 G3 G4

  • 结果分析

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JvvgaXYh-1692215418654)(media/16921742285760/16921809215912.jpg)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1r8mMi44-1692215418654)(media/16921742285760/16921818296992.jpg)]
P值小于0.05， 说明模型在95%的水平下拒绝原假设，通过了联合显著性检验，说明模型是合理的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OraqDFUn-1692215418655)(media/16921742285760/16921809359312.jpg)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0iMtwXmo-1692215418656)(media/16921742285760/16921818370769.jpg)]
先看哪些值是显著的，选择置信水平，然后选择变量，开始分析。
选择置信水平为90%，这里有两个变量是显著的，团购价在其他变量不变的情况下，每增加一元，评价量减小-29.77。控制其他变量不变的情况下，分类为羊奶粉的变量比分类为牛奶粉的评价量高14894.

  • 把回归结果保存到word中

    • est store m1
    • reg2docx m1 using m1.docx, replace
    • // *** p<0.01 ** p<0.05 * p<0.1
      [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tyVdON0T-1692215418656)(media/16921742285760/16921824817070.jpg)]
    • 加上右下角的标记

  • excel数据透视图会了，数据处理能超过大部分人

  • 回归分为解释型回归和预测型回归。

    • 预测型回归一般才会更看重R^2。
    • 解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著性即可。

  • 为了更为精准的研究影响评价量的重要因素（去除量纲的影响），我们可考虑使用标准化回归系数。

  • 对数据进行标准化，就是将原始数据减去它的均数后，再除以该变量的标准差，计算得到新的变量值，新变量构成的回归方程称为标准化回归方程，回归后相应可得到标准化回归系数。

  • 标准化系数的绝对值越大，说明对因变量的影响就越大（只关注显著的回归系数哦）

  • 回归标准化后得到的系数得到影响程度，不标准化得到的系数才能拿来预测。

  • 标准化回归的命令

    • regress y x1 x2 … xk, beta
    • 系数是最后一列
      [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-S1WGFZYK-1692215418656)(media/16921742285760/16921833650579.jpg)]

  • 结果阅读：在显著的前提下，绝对值要大

  • 归一化后算得的系数会不好解释

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gQBRMqSe-1692215443131)(https://cdn.jsdelivr.net/gh/jixiuy/clouding/image-20230817034835596.png)]

这篇文章还没有配置图层利用 PicGo+Typora+Github

相关文章：

数学建模-多元线性回归笔记

数学建模笔记 1.学模型✅ 2.看专题论文并复习算法 多元线性回归 无偏性&#xff1a;预测值与真实值非常接近一致性&#xff1a;样本量无限增大&#xff0c;收敛于待估计参数的真值如何做&#xff1a;控制核心解释变量和u不相关 四类模型回归系数的解释 截距项不用考虑一元线性…...

编程日记 2023/8/17 5:59:58

云安全攻防（十二）之 手动搭建 K8S 环境搭建

手动搭建 K8S 环境搭建 首先前期我们准备好三台 Centos7 机器&#xff0c;配置如下&#xff1a; 主机名IP系统版本k8s-master192.168.41.141Centos7k8s-node1192.168.41.142Centos7k8s-node2192.168.41.143Centos7 前期准备 首先在三台机器上都执行如下的命令 # 关闭防火墙…...

编程日记 2023/8/17 5:58:57

Python学习笔记_基础篇(八)_正则表达式

1. 正则表达式基础 1.1. 简单介绍 正则表达式并不是Python的一部分。正则表达式是用于处理字符串的强大工具&#xff0c;拥有自己独特的语法以及一个独立的处理引擎&#xff0c;效率上可能不如str自带的方法&#xff0c;但功能十分强大。得益于这一点&#xff0c;在提供了正则…...

编程日记 2023/8/17 5:57:56

【洛谷 P5736】【深基7.例2】质数筛 题解（判断质数）

【深基7.例2】质数筛 题目描述 输入 n n n 个不大于 1 0 5 10^5 105 的正整数。要求全部储存在数组中&#xff0c;去除掉不是质数的数字&#xff0c;依次输出剩余的质数。 输入格式 第一行输入一个正整数 n n n&#xff0c;表示整数个数。 第二行输入 n n n 个正整数 …...

编程日记 2023/8/17 5:56:54

C语言好题解析（一）

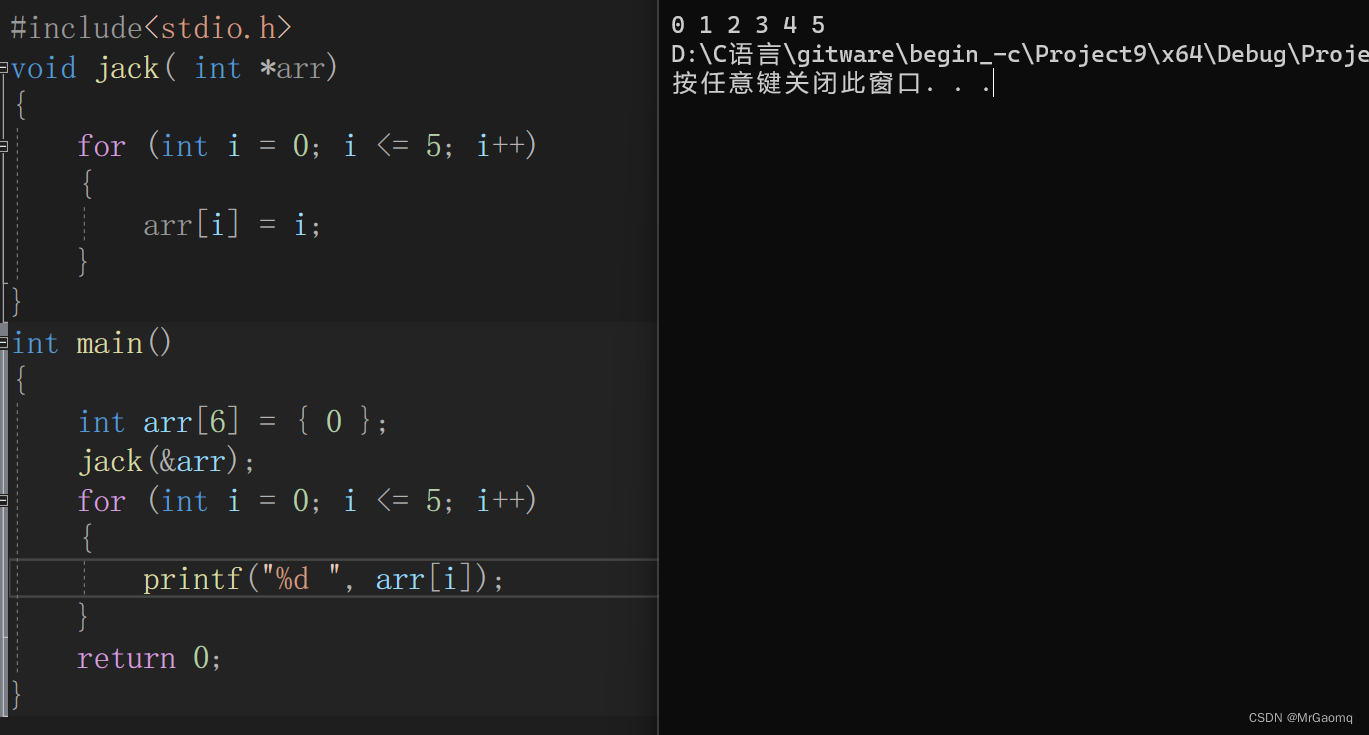
目录 选择题1选择题2选择题3选择题4编程题一 选择题1 执行下面程序&#xff0c;正确的输出是&#xff08; &#xff09;int x 5, y 7; void swap() {int z;z x;x y;y z; } int main() {int x 3, y 8;swap();printf("%d,%d\n",x, y);return 0; }A: 5,7 B: …...

编程日记 2023/8/17 5:55:52

uniapp微信小程序区分正式版，开发版，体验版

小程序代码区分是正式版&#xff0c;开发版&#xff0c;还是体验版 通常正式和开发环境需要调用不同域名接口&#xff0c;发布时需要手动更换 或者有些东西不想在正式版显示&#xff0c;只在开发版体验版中显示&#xff0c;也需要去手动隐藏 官方没有明确给出判断环境的方法&a…...

编程日记 2023/8/17 5:54:50

更多openEuler镜像加入AWS Marketplace！

自2023年7月openEuler 22.03 LTS SP1正式登陆AWS Marketplace后&#xff0c;openEuler社区一直持续于在AWS上提供更多版本。 目前&#xff0c;openEuler22.03 LTS SP1 ,SP2两个版本及 x86 arm64两种架构的四个镜像均可通过AWS对外提供&#xff0c;且在亚太及欧洲15个Region开放…...

编程日记 2023/8/17 5:53:48

【BASH】回顾与知识点梳理（二十四）

【BASH】回顾与知识点梳理 二十四 二十四. 权限规划和身份切换24.1 主机的细部权限规划&#xff1a;ACL 的使用什么是 ACL 与如何支持启动 ACL如何启动 ACL 24.2 ACL 的设定技巧&#xff1a; getfacl, setfaclsetfacl 指令用法介绍及最简单的『 u:账号:权限 』设定getfacl 指令…...

编程日记 2023/8/17 5:52:47

CSRF

CSRF CSRF&#xff0c;跨站域请求伪造&#xff0c;通常攻击者会伪造一个场景&#xff08;例如一条链接&#xff09;&#xff0c;来诱使用户点击&#xff0c;用户一旦点击&#xff0c;黑客的攻击目的也就达到了&#xff0c;他可以盗用你的身份&#xff0c;以你的名义发送恶意请…...

编程日记 2023/8/17 5:51:46

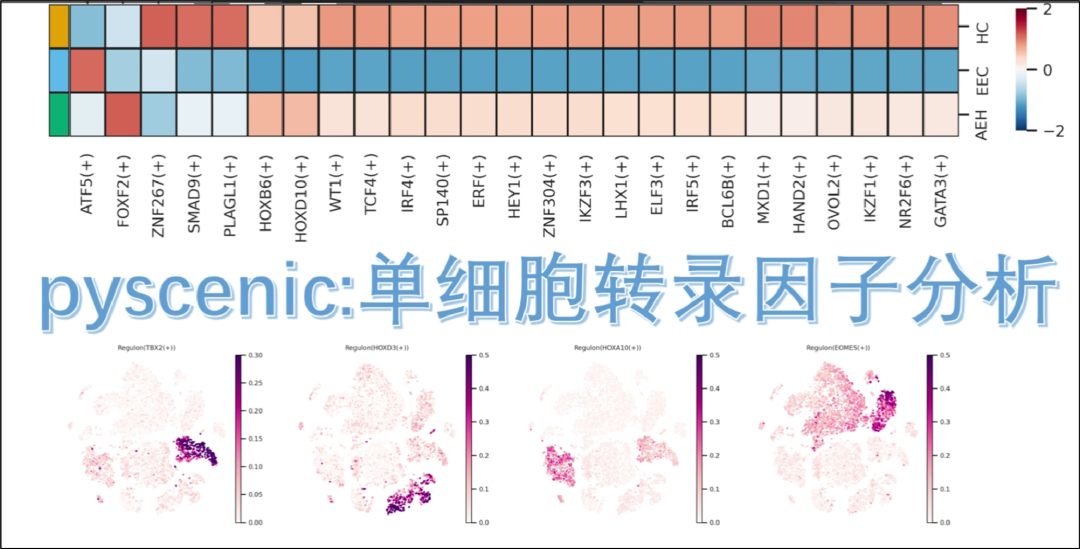
pyscenic分析：视频教程

我们之前更新过pyscenic的教程&#xff1a;pySCENIC单细胞转录因子分析更新&#xff1a;数据库、软件更新。我们也说过&#xff0c;我们号是放弃R语言版的SCENIC的分析了&#xff0c;因为它比较耗费计算资源和时间&#xff0c;所以我们的单细胞转录因子分析教程都是基于pysceni…...

编程日记 2023/8/17 5:50:45

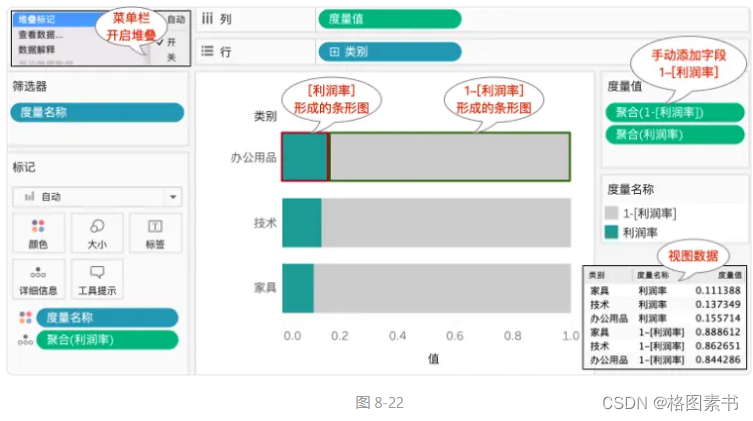
可视化绘图技巧100篇进阶篇（九）-三维百分比堆积条形图（3D Stacked Percentage Bar Chart）

目录 前言 适用场景 绘图工具及代码实现 帆软 实现思路 方案一&#xff1a;使用计算指标 上传数据 添加组件 生成图表 添加计算字段 生成分区柱形图 生成百分比堆积条形图 美化图表 设置标签 设置颜色 效果查看 PC 端 移动端 方案二&#xff1a;使用自助数…...

编程日记 2023/8/17 5:49:44

js实现将文本转PDF格式并下载到本地

html里面需要引入jspdf.umd.min.js和FileSaver.js jspdf.umd.min.js&#xff1a;https://www.npmjs.com/package/jspdf FileSaver.js&#xff1a;https://download.csdn.net/download/weixin_45791806/87272893?spm1001.2014.3001.5503 同时项目的根部目录也需要引入SimHei.tt…...

编程日记 2023/8/17 5:48:42

Servlet+JDBC实战开发书店项目讲解第四篇：登录实现

ServletJDBC 实战开发书店项目讲解第四篇&#xff1a;登录注册实现 在本篇博客中&#xff0c;我们将继续讲解 ServletJDBC 实战开发书店项目。这次我们将重点讲解如何实现登录和注册功能。 1. 创建数据库表 首先&#xff0c;我们需要在数据库中创建两个表&#xff0c;一个用…...

编程日记 2023/8/17 5:47:41

HarmonyOS NEXT新能力，一站式高效开发HarmonyOS应用

2023年8月6日华为开发者大会2023&#xff08;HDC.Together&#xff09;圆满收官&#xff0c;伴随着HarmonyOS 4的发布&#xff0c;华为向开发者发布了汇聚所有最新开发能力的HarmonyOS NEXT开发者预览版&#xff0c;并分享了围绕“一次开发&#xff0c;多端部署” “可分可合&a…...

编程日记 2023/8/17 5:46:39

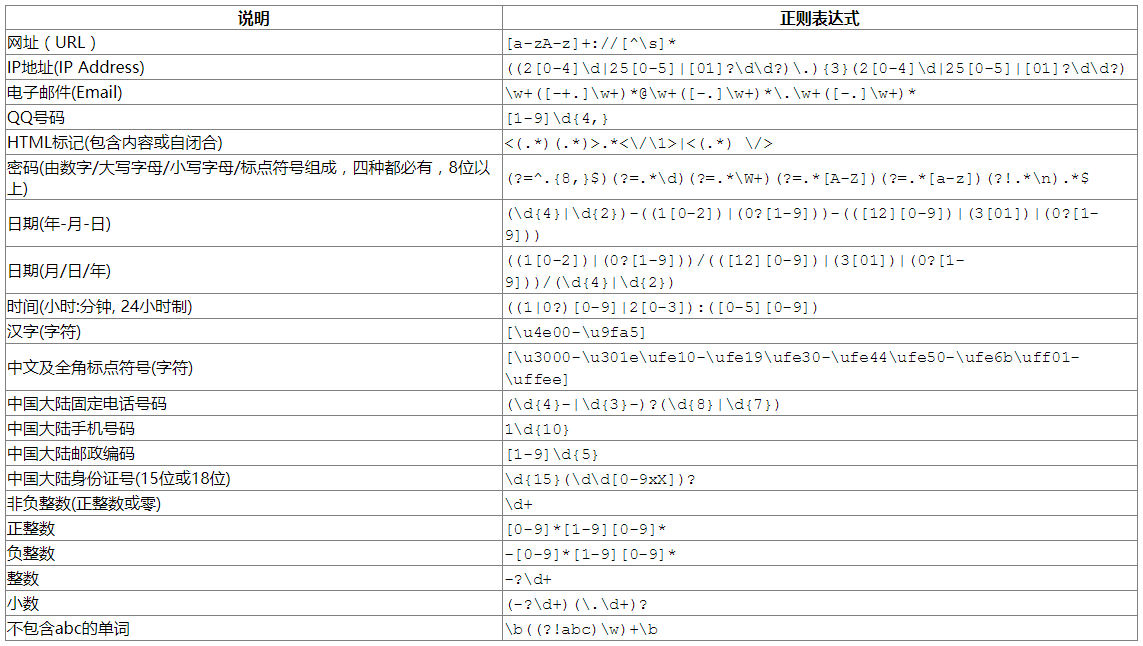
【Java从0到1学习】09 正则表达式

1. 正则表达式概述 在编写处理字符串的程序或网页时&#xff0c;经常会有查找符合某些复杂规则的字符串的需要。正则表达式就是用于描述这些规则的工具。换句话说&#xff0c;正则表达式就是记录文本规则的代码。 正则表达式&#xff0c;又称正规表示法、常规表示法&#xff…...

编程日记 2023/8/17 5:45:38

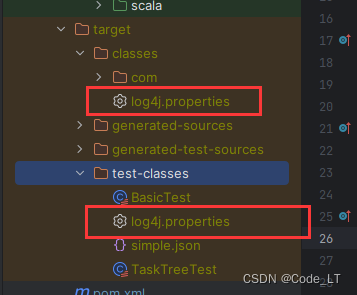
log4j:WARN No appenders could be found for logger问题

本文将idea场景下的使用。 IDEA中&#xff0c;将配置文件命名为log4j.properties&#xff08;该命名才会被自动加载&#xff09;&#xff0c; 并放到某个目录下&#xff08;通常放到resources目录&#xff09;&#xff0c;并在resources上右键&#xff0c;找到Mark Directory a…...

编程日记 2023/8/17 5:44:37

【Java】批量生成条形码-itextpdf

批量生成条形码 Controller ApiOperation("商品一览批量生成商品条形码")PostMapping("/batchGenerateProdBarCode")public void batchGenerateProdBarCode(RequestBody ProductListCondition productListCondition,HttpServletResponse response){import…...

编程日记 2023/8/17 5:43:33

SpringBoot登录、退出、获取用户信息的session处理

1、登录方法&#xff1a;login PostMapping("/user/login")public ResponseVo<User> login(Valid RequestBody UserLoginForm userLoginForm,HttpSession session) {ResponseVo<User> userResponseVo userService.login(userLoginForm.getUsername(), …...

编程日记 2023/8/17 5:42:32

【软件测试】随笔系统测试报告

博主简介&#xff1a;想进大厂的打工人博主主页&#xff1a;xyk:所属专栏: 软件测试 随笔系统采用 SSM 框架前后端分离的方法实现&#xff0c;本文主要针对功能&#xff1a;登录&#xff0c;注册&#xff0c;注销&#xff0c;写随笔&#xff0c;删除随笔&#xff0c;随笔详情页…...

编程日记 2023/8/17 5:41:31

vue中使用html2canvas+jsPDF实现pdf的导出

导入依赖 html2canvas依赖 npm install html2canvasjspdf依赖 npm install jspdfpdf导出 以导出横向&#xff0c;A4大小的pdf为例 规律&#xff1a;1. html2canvas 中&#xff0c;在保持jsPDF中的宽高不变的情况下&#xff0c;设置html2canvas中的 width 和 height 值越小&a…...

编程日记 2023/8/17 5:40:29

Linux学习之firewallD

systemctl status firewalld.service查看一下firewalld服务的状态&#xff0c;发现状态是inactive (dead)。 systemctl start firewalld.service启动firewalld&#xff0c;systemctl status firewalld.service查看一下firewalld服务的状态&#xff0c;发现状态是active (runni…...

编程日记 2023/8/17 5:39:28

【JS学习】Object.assign 用法介绍

Object.assign 是ES6中的一个方法。该方法能够实现对象的浅复制以及对象合并。Object.assign 并不会修改目标对象本身&#xff0c;而是返回一个新的对象&#xff0c;其中包含了所有源对象的属性。 例1 2个对象合并 const target { a: 1, b: 2 }; const source { b: 3, c: 4…...

编程日记 2023/8/17 5:38:25

【uni-app报错】获取用户收货地址uni.chooseAddress()报错问题

chooseAddress:fail the api need to be declared in …e requiredPrivateInf 原因&#xff1a; 小程序配置 / 全局配置 (qq.com) 解决&#xff1a; 登录小程序后台申请接口 按照流程申请即可 在项目根目录中找到 manifest.json 文件&#xff0c;在左侧导航栏选择源码视图&a…...

编程日记 2023/8/17 5:37:24

机器学习、cv、nlp的一些前置知识

为节省篇幅&#xff0c;不标注文章来源和文章的问题场景。大部分是我的通俗理解。 文章目录 向量关于向量的偏导数&#xff1a;雅可比矩阵二阶导数矩阵&#xff1a;海森矩阵随机变量随机场伽马函数beta分布数学术语坐标上升法协方差训练集&#xff0c;验证集&#xff0c;测试集…...

编程日记 2023/8/17 5:36:20

Steam 灵感的游戏卡悬停效果

先看效果&#xff1a; 再看代码&#xff08;查看更多&#xff09;&#xff1a; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Steam 灵感的游戏卡悬停效果</title><style>* {margin: …...

编程日记 2023/8/17 5:35:19

[Openwrt]一步一步搭建MT7981A uboot、atf、openwrt-21.02开发环境操作说明

安装ubuntu-18.04 软件安装包 ubuntu-18.04-desktop-amd64.iso 修改ubuntu管理员密码 sudo passwd [sudo] password for w1804: Enter new UNIX password: Retype new UNIX password: passwd: password updated successfully 更新ubuntu源 备份源 sudo cp /etc/apt/so…...

编程日记 2023/8/17 5:34:18

Unity C# 之 Azure 微软SSML语音合成TTS流式获取音频数据以及表情嘴型 Animation 的简单整理

Unity C# 之 Azure 微软SSML语音合成TTS流式获取音频数据以及表情嘴型 Animation 的简单整理 目录 Unity C# 之 Azure 微软SSML语音合成TTS流式获取音频数据以及表情嘴型 Animation 的简单整理 一、简单介绍 二、实现原理 三、注意事项 四、实现步骤 五、关键代码 一、简…...

编程日记 2023/8/17 5:33:16

安全学习DAY16_信息打点-CDN绕过

信息打点-CDN绕过 文章目录 信息打点-CDN绕过本节思维导图相关链接&工具站&项目工具前置知识&#xff1a;CDN配置&#xff1a;配置1&#xff1a;加速域名-需要启用加速的域名配置2&#xff1a;加速区域-需要启用加速的地区配置3&#xff1a;加速类型-需要启用加速的资源…...

编程日记 2023/8/17 5:32:15

genism word2vec方法

文章目录 概述使用示例模型的保存与使用训练参数详解&#xff08;[原链接](https://blog.csdn.net/weixin_44852067/article/details/130221655)&#xff09;语料库训练 概述 word2vec是按句子来处理的Sentences(句子们) 使用示例 from gensim.models import Word2Vec #sent…...

编程日记 2023/8/17 5:31:14

vue3自定义样式-路由-axios拦截器

基于vue,vite和elementPlus 基于elementPlus自定义样式 history模式的路由 在根目录配置jsconfig.json&#xff0c;添加json的配置项。输入自动联想到src目录&#xff0c;是根路径的别名拦截器 如果存在多个接口地址&#xff0c;可以配置多个axios实例 数据持久化之后&#x…...

编程日记 2023/8/17 5:30:13