第三章 图论 No.10无向图的双连通分量
文章目录
- 定义
- Tarjan求e-DCC
- Tarjan求v-DCC
- 395. 冗余路径
- 1183. 电力
- 396. 矿场搭建
定义
无向图有两种双连通分量
- 边双连通分量,e-DCC
- 点双连通分量,v-DCC
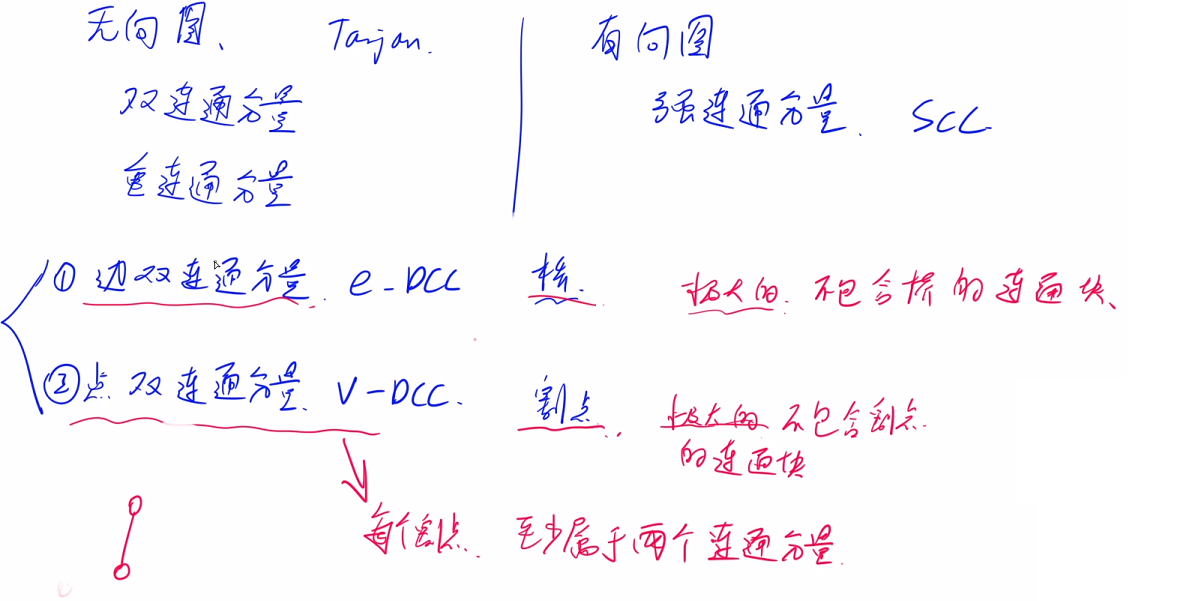
桥:删除这条无向边后,图变得不连通,这条边被称为桥
边双连通分量:极大的不含有桥的连通区域,说明无论删除e-DCC中的哪条边,e-DCC依旧连通 (该连通分量的任意边属于原图中的某条环)。此外,任意两点之间一定包含两条不相交(无公共边)的路径
割点:删除该点(与该点相关的边)后,图变得不连通,这个点被称为割点
点双连通分量:极大的不含有割点的连通区域
一些性质:
- 每个割点至少属于两个连通分量
- 任何两个割点之间的边不一定是桥,任何桥两边的端点不一定是割点,两者没有必然联系,一个点连通分量也不一定是边连通分量
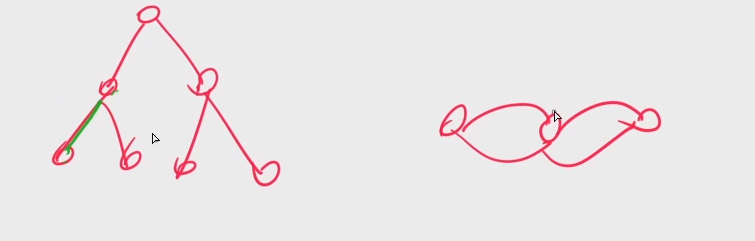
Tarjan求e-DCC
无向图不存在横叉边
和有向图的强连通分量类似,引入dfn和low两个数组
如何找到桥?判断x->y的y是否能走到x之前(祖先节点),如果能走到,x和y在一个环中,删除这条边,其他点依然是连通的
所以x->y为桥:dfn[x] < low[y]
如何找到所有边的双连通分量?
- 删除所有桥
- 或者用stk辅助,若
dfn[x] == low[x],说明x出发一定走不到x的祖先节点,那么x和其父节点之间的边是桥,此时还在stk中的点为e-DCC的节点
这里使用第二种方式,模板:
void tarjan(int x, int from)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y, i);low[x] = min(low[x], low[y]);}else if (i != (from ^ 1))low[x] = min(low[x], dfn[y]);if (dfn[x] < low[y])st[i] = st[i ^ 1] = true;}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ];id[y] = cnt;} while (x != y);}
}
由于无向图要存储两条有向边,并且从数组的0下标开始存储,所以0,1、2,3…这样一对的边是互相反向的边,即i和i ^ 1为反向边
为什么与有向图的强连通分量不同,边双连通分量不需要使用st数组以标记栈中的元素?
因为无向图不存在横叉边的概念,就不会出现:x->y而y的dfn小于x,因为在无向图中y一定会向x遍历
Tarjan求v-DCC
如何求割点?low[y] >= dfn[x],删除x节点后,y就是一颗独立的子树
- 如果x不是根节点,那么x是一个割点
- 如果x是根节点,至少有两个y满足以上关系
求割点的板子:
void tarjan(int x)
{dfn[x] = low[x] = ++ tp;int t = 0;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]) t ++ ;}else low[x] = min(low[x], dfn[y]);}if (x != root) t ++ ;ans = max(ans, t);
}
将每个v-DCC向其包含的割点连一条边
缩点后,边的数量不会增加,点的数量可能会增加到两倍
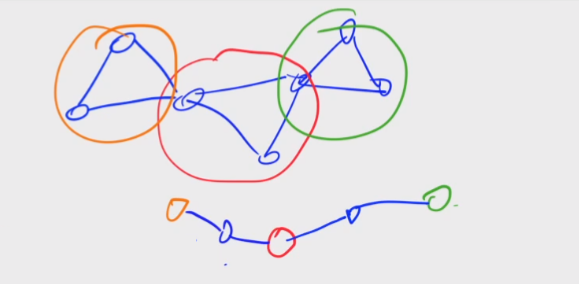
tarjan求v-DCC与割点的板子:
一个孤立的点也是一个v-DCC,这里需要特判
若满足条件:low[y] >= dfn[x],那么y的子树与x一起就是一个v-DCC
对于该节点是否是割点还需要特判,若该节点为根,并且与该节点相连的连通块数量为1,那么该节点就不是一个割点
void tarjan(int x)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt ] = x;if (x == root && h[x] == -1){++ dcnt;dcc[dcnt].push_back(x);return;}int t = 0; // 与x相连的连通块数量for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]){dcnt ++, t ++ ;if (x != root || t > 1) st[x] = true; // x为割点int u;do {u = stk[tt -- ];dcc[dcnt].push_back(u);} while (u != y);dcc[dcnt].push_back(x);}}else low[x] = min(low[x], dfn[y]);}
}
395. 冗余路径
395. 冗余路径 - AcWing题库
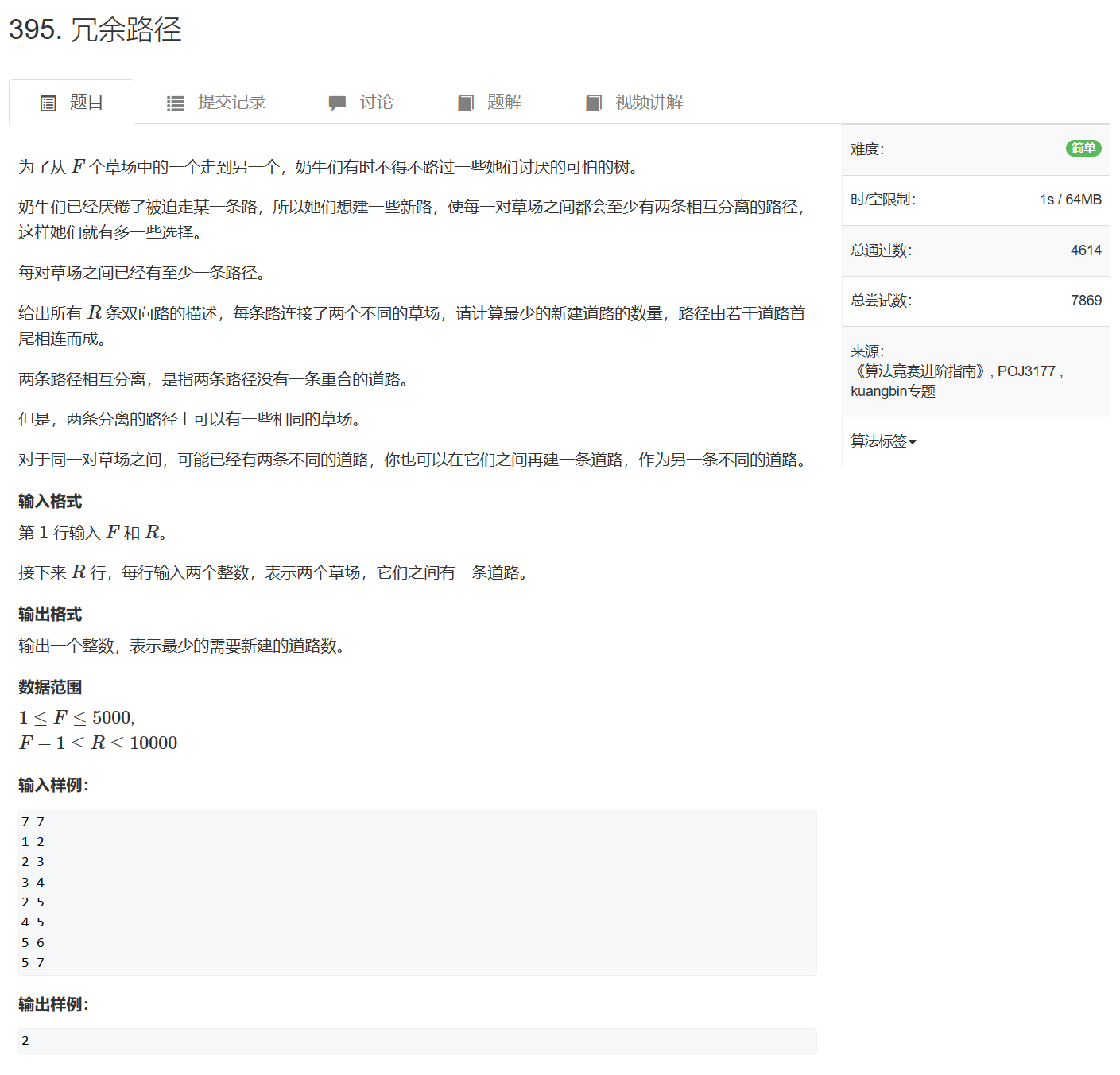
任意两点间都存在两条没有重复边的路径,等价于整个图是一个双连通分量
将无向连通图的边双连通分量缩点后,得到的结构是一颗树,因为边双连通分量是不包含桥的结构,缩点后,图中只含有桥,即删除任意一条边后,图成为两个连通块,这是一个树结构
为了满足题意,需要向这颗树中添加边,使之成为边连通分量,那么要加几条边?
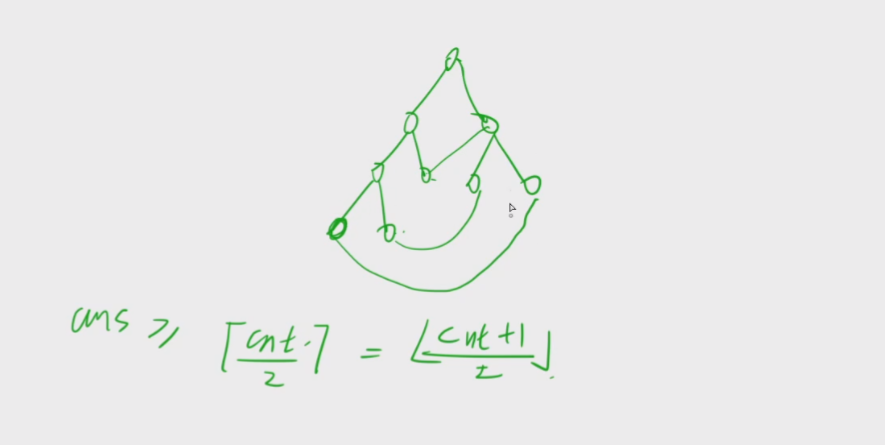
连接所有叶子节点,使这颗树结构成为双连通分量,至少需要加 [ ( c n t + 1 ) / 2 ] [(cnt + 1) / 2] [(cnt+1)/2]然后再下取整的边数,也就是将每个叶子节点相连,使环满足双连通分量的性质
注意cnt为1时需要特判
#include <iostream>
#include <cstring>
using namespace std;const int N = 5010, M = 10010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt, id[N];
bool st[N]; int d[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x, int from)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y, i);low[x] = min(low[x], low[y]);if (dfn[x] < low[y])st[i] = st[i ^ 1] = true;}else if (i != (from ^ 1))low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ];id[y] = cnt;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y), add(y, x);}tarjan(1, -1);for (int i = 0; i < idx; i ++ )if (st[i])d[id[e[i]]] ++ ;int res = 0;for (int i = 1; i <= cnt; ++ i )if (d[i] == 1) res ++ ;if (cnt == 1) puts("0");else printf("%d\n", (res + 1) / 2);return 0;
}
debug:^的优先级小于!=
可以不使用st数组标记桥:
#include <iostream>
#include <cstring>
using namespace std;const int N = 5010, M = 10010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt, id[N];
int d[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x, int from)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y, i);low[x] = min(low[x], low[y]);}else if (i != (from ^ 1))low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ];id[y] = cnt;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y), add(y, x);}tarjan(1, -1);for (int x = 1; x <= n; ++ x )for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y];if (a != b) d[a] ++ ;}int res = 0;for (int i = 1; i <= cnt; i ++ )if (d[i] == 1) res ++ ;if (cnt == 1) puts("0");else printf("%d\n", (res + 1) / 2);return 0;
}
1183. 电力
1183. 电力 - AcWing题库
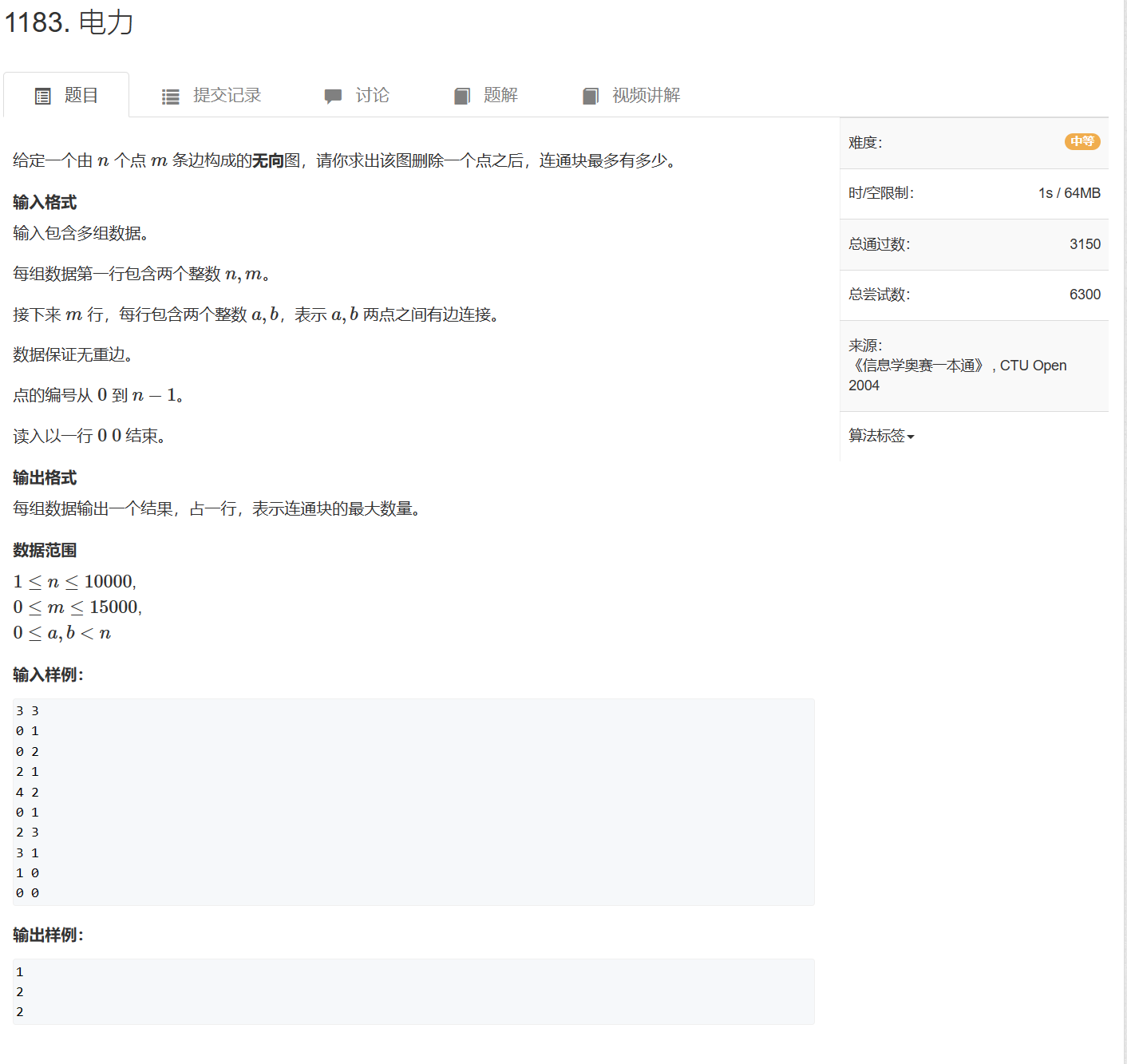
枚举所有割点,判断删除哪个割点后剩余的连通块数量最大
剩余的连通块数量为ans + cnt - 1
由于题目给定的图并不是一个连通图,所以可能存在多个连通块,cnt为连通块数量
枚举所有割点只能在一个连通块中枚举,此时其他连通块的数量为cnt - 1
又因为ans为删除割点后,剩余连通块最多的值,所以答案为ans + cnt - 1
这题的点编号从0开始
#include <iostream>
#include <cstring>
using namespace std;const int N = 10010, M = 30010;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int ans, n, m, root;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{dfn[x] = low[x] = ++ tp;int t = 0;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]) t ++ ;}else low[x] = min(low[x], dfn[y]);}if (x != root) t ++ ;ans = max(ans, t);
}int main()
{while (scanf("%d%d", &n, &m), n | m){memset(h, -1, sizeof(h));memset(dfn, 0, sizeof(dfn));idx = tp = cnt = ans = 0;int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y), add(y, x);}for (root = 0; root < n; ++ root){if (!dfn[root]) {cnt ++ ;tarjan(root);}}printf("%d\n", ans + cnt - 1);}return 0;
}
debug:dfn数组没有置空
396. 矿场搭建
396. 矿场搭建 - AcWing题库


对于图中的每个连通块,分情况讨论:
- 若连通块无割点,那么任意设置两个救援点即可
- 若连通块中有割点,缩点:将每个割点依然看成一个点,将每个v-DCC向其包含的割点连线
- 缩点后得到一棵树,对于叶子节点,需要建立救援点。因为只有一个点与其相连,若该点坍塌,需要在内部建立救援点。假设内部节点数量为cnt,方案数为cnt-1个,去除割点
- 对于非叶子节点,无需建立救援点,因为无论与之相连的哪个割点坍塌,该节点都能走到叶子节点,而叶子节点已经建立救援点
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;typedef unsigned long long ULL;
const int N = 1010, M = 1010;
int h[N], e[M], ne[M], idx;
vector<int> dcc[N];
int dcnt, root;
int dfn[N], low[N], tp;
int stk[N], tt;
bool st[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{low[x] = dfn[x] = ++ tp;stk[ ++ tt ] = x;if (x == root && h[x] == -1){dcnt ++ ;dcc[dcnt].push_back(x);return;}int t = 0;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);if (low[y] >= dfn[x]){t ++, dcnt ++ ;if (x != root || t > 1) st[x] = true;int u;do {u = stk[tt -- ];dcc[dcnt].push_back(u);} while (u != y);dcc[dcnt].push_back(x);}}else low[x] = min(low[x], dfn[y]);}
}int main()
{int T = 1;while (scanf("%d", &m), m){for (int i = 0; i < N; ++ i ) dcc[i].clear();memset(h, -1, sizeof(h));memset(dfn, 0, sizeof(dfn));memset(st, false, sizeof(st));tp = dcnt = idx = tt = n = 0;for (int i = 0; i < m; ++ i ){int x, y;scanf("%d%d", &x, &y);add(x, y), add(y, x);n = max(n, x), n = max(n, y);}for (root = 1; root <= n; ++ root )if (!dfn[root]) tarjan(root);ULL sum = 1; int ans = 0;for (int i = 1; i <= dcnt; ++ i ){int t = 0;for (int j = 0; j < dcc[i].size(); ++ j )if (st[dcc[i][j]]) t ++ ;if (t == 0) {if (dcc[i].size() > 1) ans += 2, sum *= ((ULL)dcc[i].size() * (dcc[i].size() - 1)) / 2;else ans ++ ;}else if (t == 1) ans += 1, sum *= (dcc[i].size() - 1);}printf("Case %d: %d %llu\n", T ++ , ans, sum);}return 0;
}
debug:由于多组测试数据,没有初始化干净所有元素
最后统计救援点数量以及方案总数时,没有对孤立点进行特判
相关文章:

第三章 图论 No.10无向图的双连通分量
文章目录 定义Tarjan求e-DCCTarjan求v-DCC395. 冗余路径1183. 电力396. 矿场搭建 定义 无向图有两种双连通分量 边双连通分量,e-DCC点双连通分量,v-DCC 桥:删除这条无向边后,图变得不连通,这条边被称为桥 边双连通分…...
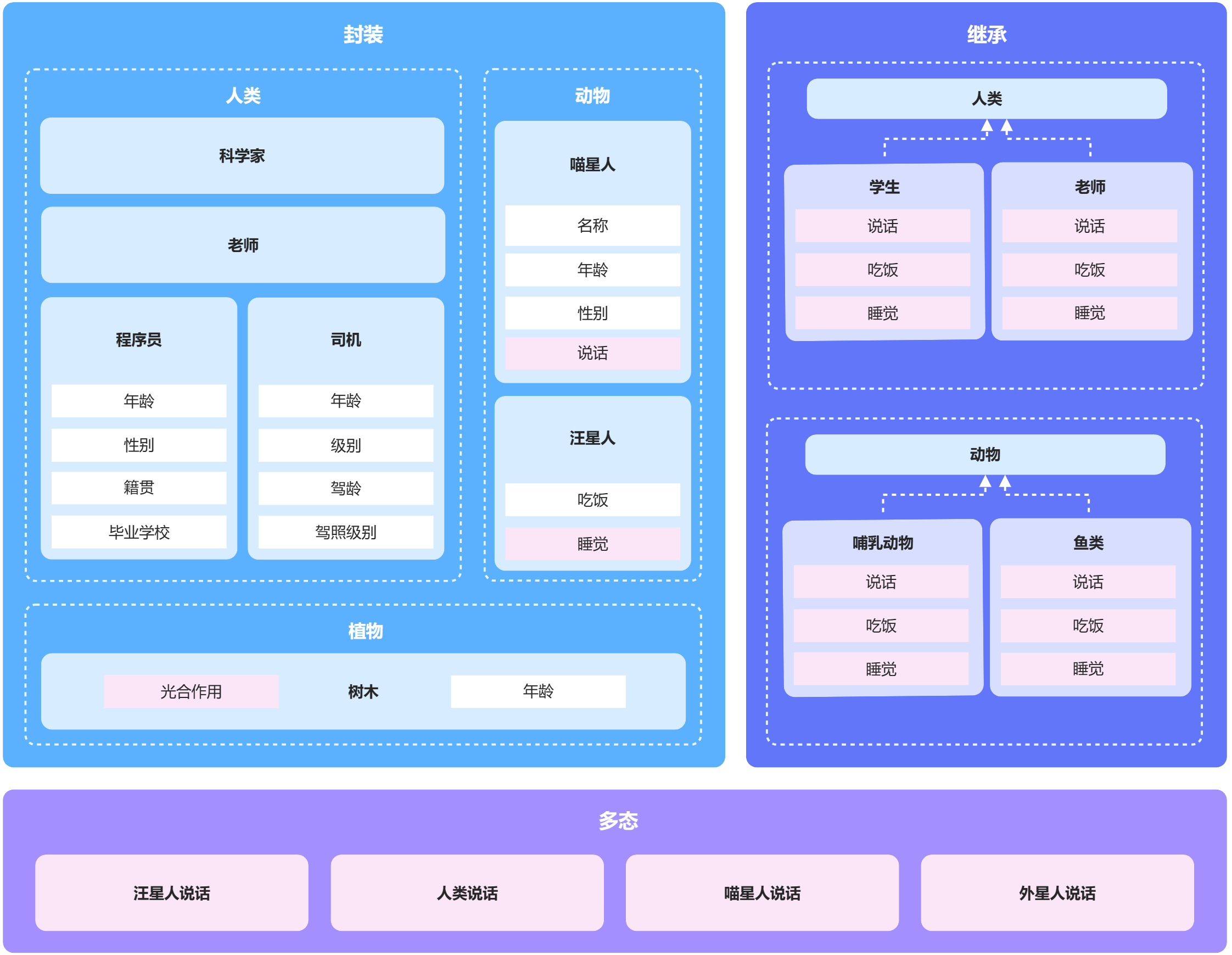
Java学习手册——第二篇面向对象程序设计
Java学习手册——第二篇面向对象 1. 结构化程序设计2. 面向对象 第一章我们已经介绍了Java语言的基础知识,也知道他能干什么了, 那我们就从他的设计思想开始入手吧。 接触一个语言之前首先要知道他的大方向,设计思想是什么样的, 这…...
Redis实战:Redis的安装及简单使用
本片将介绍 Redis 的安装及简单使用 文章目录 1、Redis安装1.1、Windows下Redis的安装1.2、Linux下Redis的安装1.3、Mac下Redis的安装(使用Homebrew) 2、Redis使用2.1、启动服务端客户端2.2、Redis简单命令 3、Redis命令大全 1、Redis安装 1.1、Windows…...
Linux学习之初识Linux
目录 一.Linux的发展历史及概念 1.什么是Linux UNIX发展的历史: Linux发展历史: 2. 开源 商业化发行版本 二. 如何搭建Linux环境 Linux 环境的搭建方式主要有三种: 1. 直接安装在物理机上 2. 使用虚拟机软件 3. 使用云服务器 三. …...

神经网络基础-神经网络补充概念-29-为什么使用深层表示
概念 深层表示(Deep Representation)是指在深度神经网络的多个隐藏层中逐层提取和学习数据的特征表示。 使用深层表示的原因 高维特征提取:深层神经网络可以从原始数据中自动学习高维抽象特征。每个隐藏层都对数据进行一些变换,…...

2023最新水果编曲软件FL Studio 21.1.0.3267音频工作站电脑参考配置单及系统配置要求
音乐在人们心中的地位日益增高,近几年音乐选秀的节目更是层出不穷,喜爱音乐,创作音乐的朋友们也是越来越多,音乐的类型有很多,好比古典,流行,摇滚等等。对新手友好程度基本上在首位,…...

边缘计算:下一代计算模式的突破
章节一:引言 随着物联网、人工智能和大数据等技术的不断发展,计算需求变得越来越复杂,传统的云计算模式已经难以满足快速增长的数据处理需求。在这样的背景下,边缘计算作为一种全新的计算模式崭露头角,为我们带来了更加…...

连接不上手机,adb devices为空:
首先说明一下,我是已经安装了android studio,也配置了环境变量,但是还是连接不上手机 解决方案: 1.打开开发者模式 https://product.pconline.com.cn/itbk/sjtx/sjwt/1424/14246015.html 2.开启usb调试 https://baiyunju.cc/10770 最后成功…...
vuex学习总结
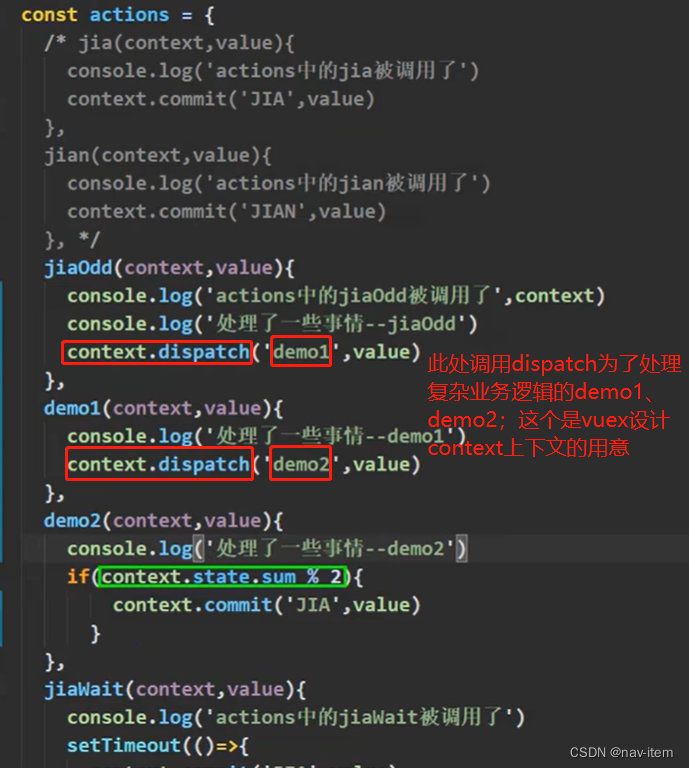
一、vuex工作原理 工作流程:需求:改变组件count的sun变量的值,先调用dispatch函数传入jia函数和要改变的值给actions(这个actions里面必须有jia这个函数);actions收到后调用commit函数将jia方法和值传给mut…...

11. Docker Swarm(二)
1、前言 上一篇中我们利用Docker Swarm搭建了基础的集群环境。那么今天我们就来验证以下该集群的可用性。上一篇的示例中,我创建了3个实例副本,并且通过访问http://192.168.74.132:8080得到我们的页面。 2、验证高可用 1)我们可以通过以下命…...

注册中心Eureka和Nacos,以及负载均衡Ribbon
1.初识微服务 1.1.什么是微服务 微服务,就是把服务拆分成为若干个服务,降低服务之间的耦合度,提供服务的独立性和灵活性。做到高内聚,低耦合。 1.2.单体架构和微服务架构的区别: 单体架构:简单方便&#…...

php+tcpdf生成pdf:中文乱码
亲测成功,感谢分享! 查看原文 TCPDF是一个生成PDF的不错的库,可惜,官方对包括中文在内的东亚字体支持不怎么样的。 场景:某项目需要根据数据库信息生成pdf格式的发票,考虑采用稳定的tcpdf,虽然…...

【AI实战】BERT 文本分类模型自动化部署之 dockerfile
【AI实战】BERT 文本分类模型自动化部署之 dockerfile BERTBERT 文本分类模型基于中文预训练bert的文本分类模型针对多分类模型的loss函数样本不均衡时多标签分类时 dockerfile编写 dockerfilebuild镜像运行docker测试服务 参考 本文主要介绍: 基于BERT的文本分类模…...
深入理解 Flutter 图片加载原理 | 京东云技术团队
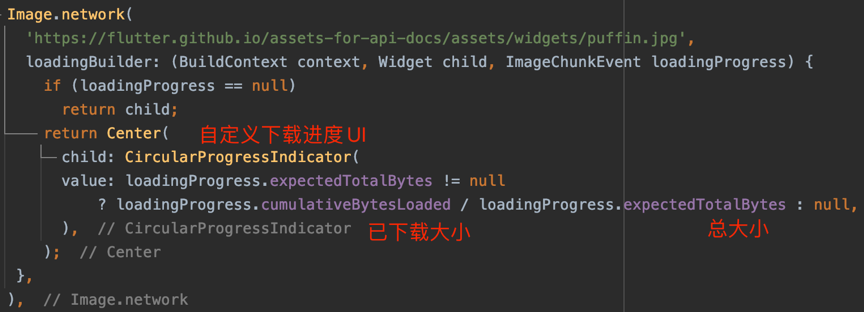
前言 随着Flutter稳定版本逐步迭代更新,京东APP内部的Flutter业务也日益增多,Flutter开发为我们提供了高效的开发环境、优秀的跨平台适配、丰富的功能组件及动画、接近原生的交互体验,但随之也带来了一些OOM问题,通过线上监控信息…...

Spring Boot 支持多种环境,包括开发环境、测试环境、预发布环境和生产环境。
Spring Boot 支持多种环境,包括开发环境、测试环境、预发布环境和生产环境。不同的环境具有不同的配置,可以在不同的环境中对应用程序进行测试、验证和部署。以下是每种环境的用途和相应的代码案例。 开发环境 开发环境是开发人员在本地进行开发的环境&…...
Ctfshow web入门 命令执行RCE篇 web29-web77 与 web118-web124 详细题解 持续更新中(预计8.18完成)~
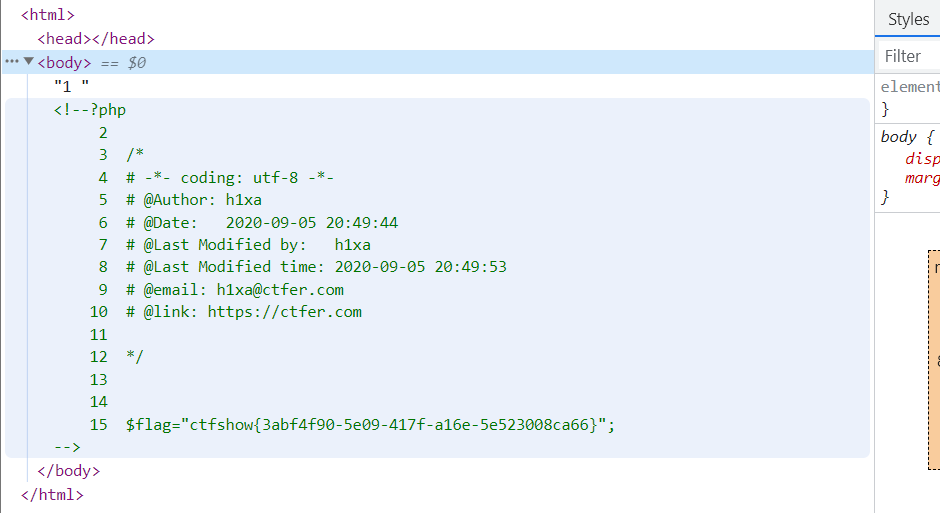
Ctfshow 命令执行 web29 pregmatch是正则匹配函数,匹配是否包含flag,if(!preg_match("/flag/i", $c)),/i忽略大小写 可以利用system来间接执行系统命令 flag采用f*绕过,或者mv fl?g.php 1.txt修改文件名,…...

合宙Air724UG LuatOS-Air script lib API--wifiRil
wifiRil Table of Contents wifiRil wifiRil.regRsp(head, fnc, typ, formt) wifiRil.regUrc(prefix, handler) wifiRil.deRegUrc(prefix) wifiRil.request(cmd, arg, onrsp, delay, param) wifiRil 模块功能:esp8266 wifi模块AT命令交互管理 wifiRil.regRsp(head,…...

python读取word/pdf文档,指定文字内容和图片
读编号转文件夹目录然后放图片进去那个 一 先将word转为PDF pdf 读起来比较方便, 按页码读取文件: import pdfplumber from PIL import Image import cv2 import numpy as np import re import os import logging import iodef create_folder(folder_name):if not…...

零售行业供应链管理核心KPI指标(二) – 线上订单履行周期
一般品牌零售商有一个大的渠道就是全国连锁的商超、大卖场,非常重要的渠道,要去铺货。同类型的产品都在竞争这个大渠道,但商超、大卖场在这类产品的容量是有限的,所以各个品牌就要去争夺整个容量,看谁在有限的容量里占…...
VGG分类实战:猫狗分类
关于数据集 数据集选择的是Kaggle上的Cat and Dog,猫狗图片数量上达到了上万张。你可以通过这里进入Kaggle下载数据集Cat and Dog | Kaggle。 在我的Github仓库当中也放了猫狗图片各666张。 VGG网络 VGG的主要特点是使用了一系列具有相同尺寸 3x3 大小的卷积核进…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...
