数据结构--最短路径 Dijkstra算法
数据结构–最短路径 Dijkstra算法

Dijkstra算法
计算 b e g i n 点到各个点的最短路 \color{red}计算\ begin\ 点到各个点的最短路 计算 begin 点到各个点的最短路

如果是无向图,可以先把无向图转化成有向图

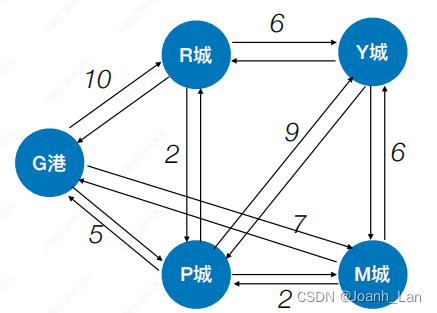
我们需要2个数组
final[] (标记各顶点是否已找到最短路径)与 dis[] (最短路径⻓度)数组
Dijkstra算法是一种用于寻找图中最短路径的算法,它的步骤如下:
- 初始化:将起始节点的最短路径设置为0,其他节点的最短路径设置为正无穷大。
- 选取最短路径最小的节点作为当前节点。
- 更新当前节点的邻居节点的最短路径:如果通过当前节点到达邻居节点的路径比邻居节点当前的最短路径更短,则更新邻居节点的最短路径。
- 标记当前节点为已访问(已经找到 b e g i n begin begin 到该点的最短路)。
- 重复步骤2 → \to → 4,直到所有节点都被访问过或者没有可达到的节点。
- 根据最短路径和前驱节点构建最短路径树或者路径数组。
以上就是Dijkstra算法的基本步骤。在实际应用中,可以使用优先队列来选取最短路径最小的节点,以提高算法的效率 (堆Dijkstra)。

V0到V2 的最短(带权)路径⻓度为:dist[2] = 9
通过 path[ ] 可知,V0到V2 的最短(带权)路径:
v 0 → v 4 → v 1 → v 2 v_0 \to v_4 \to v_1 \to v_2 v0→v4→v1→v2
Dijkstra算法的时间复杂度
时间复杂度: O ( n 2 ) 即 O ( ∣ V ∣ 2 ) O(n^2)即O(|V|^2) O(n2)即O(∣V∣2)
代码实现
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
//时间复杂是 O(n2+m), n 表示点数,m 表示边数
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i++){int t = -1; // 在还未确定最短路的点中,寻找距离最⼩的点for (int j = 1; j <= n; j++)if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;// ⽤t更新其他点的距离for (int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f)return -1;return dist[n];
}
负权值带权图问题,Dijkstra不可用
负权值带权图问题, D i j k s t r a 不可用!!! \color{red}负权值带权图问题,Dijkstra不可用!!! 负权值带权图问题,Dijkstra不可用!!!
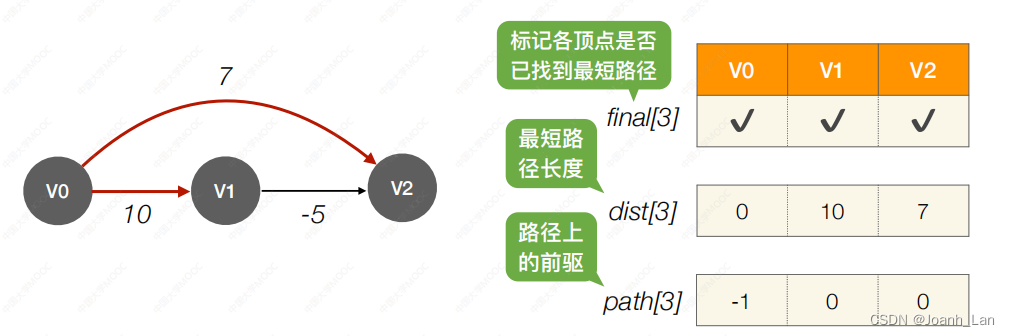
事实上 V 0 V_0 V0 到 V 2 V_2 V2 的最短带权路径⻓度为 5
结论:Dijkstra 算法不适⽤于有负权值的带权图
相关文章:

数据结构--最短路径 Dijkstra算法
数据结构–最短路径 Dijkstra算法 Dijkstra算法 计算 b e g i n 点到各个点的最短路 \color{red}计算\ begin\ 点到各个点的最短路 计算 begin 点到各个点的最短路 如果是无向图,可以先把无向图转化成有向图 我们需要2个数组 final[] (标记各顶点是否已…...
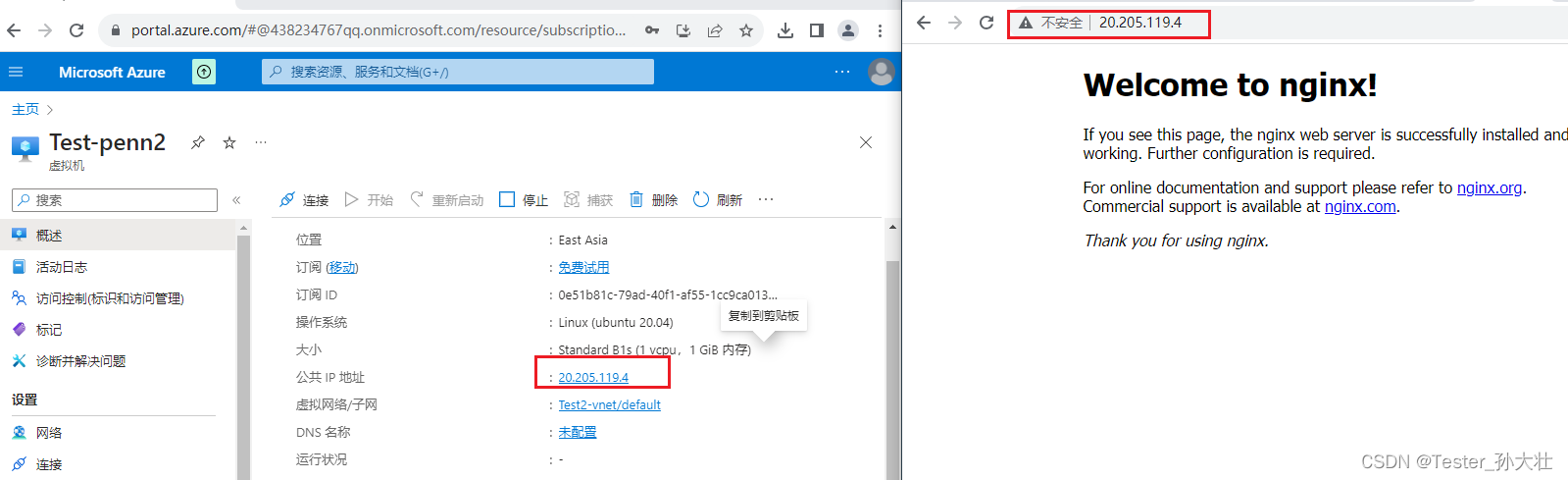
在 Linux 虚拟机上使用 Azure 自定义脚本扩展版本
参考 azure创建虚拟机,创建虚拟机注意入站端口规则开放80端口、 2.转到资源,点击扩展应用程序,创建存储账户,创建容器,上传文件,选择文件,会自动执行部署。 apt-get update -y && apt-get insta…...
W5500-EVB-PICO 做UDP Server进行数据回环测试(七)
前言 前面我们用W5500-EVB-PICO 开发板在TCP Client和TCP Server模式下,分别进行数据回环测试,本章我们将用开发板在UDP Server模式下进行数据回环测试。 UDP是什么?什么是UDP Server?能干什么? UDP (User Dataqram P…...
:项目实战(二)--elasticsearch java api 进行数据增删改查)
ES搜索引擎入门+最佳实践(九):项目实战(二)--elasticsearch java api 进行数据增删改查
本篇是这个系列的最后一篇了,在这之前可以先看看前面的内容: ES搜索引擎入门最佳实践(一)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(二)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(三)_flame.liu的博客-CSDN博客 ES搜索引擎入门最佳实践(四)_flame.liu的博…...
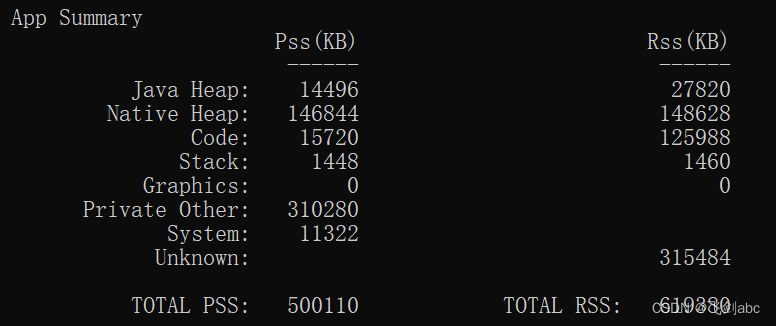
android内存分析工具记录,请利用好最后2个神器
相机见证了java内存暴增和native持续增长的问题,因此这里记录一下使用的工具情况,方便后续继续使用 一、java 内存 如果是java层的内存可以直接借助leakCanary工具,配置也很简单,直接在build.gradle中添加依赖即可: …...

安科瑞变电所运维平台在电力系统中应用分析
摘要:现代居民生活、工作对电力资源的需求量相对较多,给我国的电力产业带来了良好的发展机遇与挑战。探索电力系统基本构成, 将变电运维安全管理以及相应的设备维护工作系统性开展,能够根据项目实践工作要求,将满足要求…...
uniapp开发微信小程序使用painter将页面转换为图片并保存到本地相册
引言 我使用到painter的原因是,在uniapp开发微信小程序时,需要将一个页面的内容转换成图片保存到本地相册。 起初在网上找到很多都是在uniapp中使用 html2canvas 将网页转换成图片再jspdf将图片转换为pdf,但是这种方式在小程序环境不支持&am…...

790. 数的三次方根
文章目录 QuestionIdeasCode Question 给定一个浮点数 n ,求它的三次方根。 输入格式 共一行,包含一个浮点数 n 。 输出格式 共一行,包含一个浮点数,表示问题的解。 注意,结果保留 6 位小数。 数据范围 −10000≤…...

POSTGRESQL 关于2023-08-14 数据库自动启动文章中使用KILL 来进行配置RELOAD的问题解释...
开头还是介绍一下群,如果感兴趣Polardb ,mongodb ,MySQL ,Postgresql ,redis ,SQL SERVER ,ORACLE,Oceanbase 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请加 liuaustin3微信号 &…...

vue 使用插件高德地图--vue-amap
第一步:安装 vue-amap npm install vue-amap第二步:在你的 Vue 项目中注册 vue-amap: // main.js import Vue from vue; import VueAMap from vue-amap;Vue.use(VueAMap);VueAMap.initAMapApiLoader({// 高德开发者平台申请key值key: cc9c098…...

减速比如何计算
减速比是用来衡量机械系统中输入轴和输出轴转速之间的比例关系,通常用来描述传动装置(如齿轮传动、皮带传动等)的效果。计算减速比的公式取决于传动装置的类型。以下是一些常见传动装置的减速比计算方法: 齿轮传动: 对…...
)
HarmonyOS/OpenHarmony应用开发-ArkTSAPI组件总体分类与说明(下)
六、文本与输入 Text 显示一段文本的组件。 Span 作为Text组件的子组件,用于显示行内文本片段的组件。 Search 搜索框组件,适用于浏览器的搜索内容输入框等应用场景。 TextArea 多行文本输入框组件,当输入的文本内容超过组件宽度时会自动换行…...

势函数和鞅的停时定理
前置芝士 鞅: 鞅是一类特殊的随机过程,假设我们从一开始就在观察一场赌博游戏,现在已经得到了前t秒的观测值,那么当第t1 秒观测值的期望等于第t秒的观测值时,我们称这是一个公平赌博游戏。 具体来说,对于…...

途乐证券-炒股开户流程是怎样的?
炒股是一种危险较大但收益也相对较高的出资方法,而开户则是出资炒股的前提。跟着科技的开展,炒股开户已经能够在线完结,但流程相对来说仍是比较繁琐的。那么,炒股开户流程是怎样的呢?下面从多个视点剖析。 一、炒股开户…...
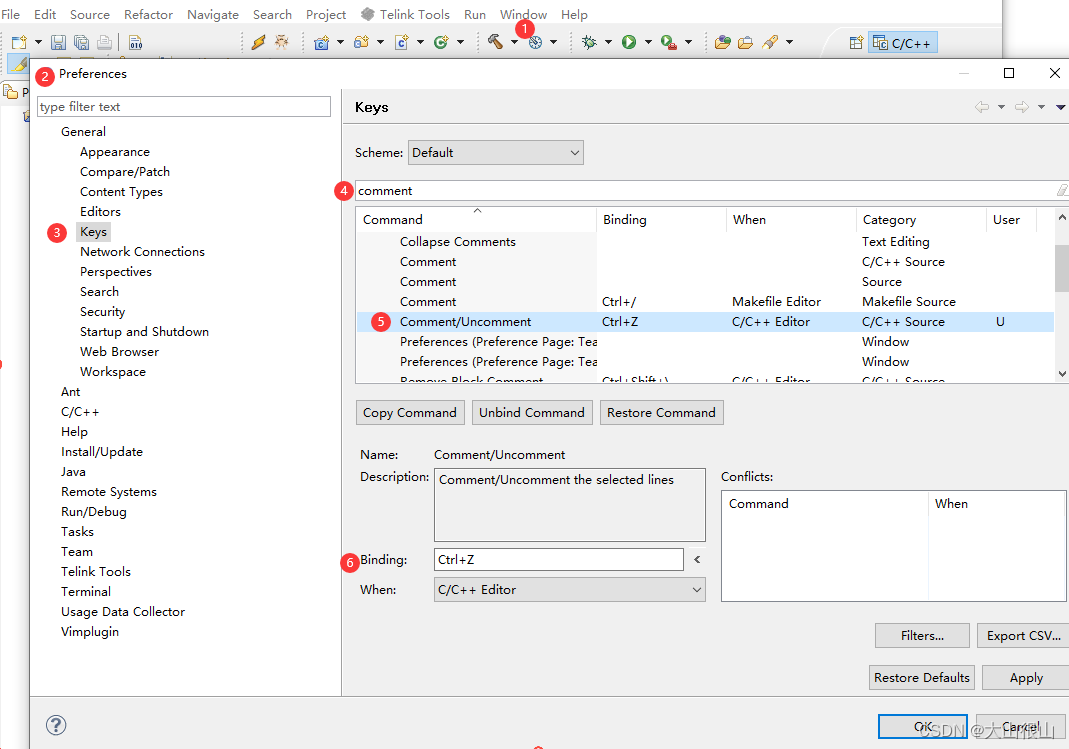
Eclipse如何设置快捷键
在eclopse设置注释行和取消注释行 // 打开eclipse,依次打开:Window -> Preferences -> General -> Key,...

刷享全球美好 中信银行信用卡推出跨境消费系列活动
来源 | 镭射财经(leishecaijing) 日前,文旅部办公厅发布通知,恢复全国旅行社及在线旅游企业经营中国公民赴有关国家和地区(第三批)出境团队旅游和“机票酒店”业务,出境跟团游国家和地区由此前…...

LeetCode算法心得——限制条件下元素之间的最小绝对差(TreeSet)
大家好,我是晴天学长,今天用到了Java一个非常实用的类TreeSet,能解决一些看起来棘手的问题。 1 )限制条件下元素之间的最小绝对差 2) .算法思路 初始化变量:n为列表nums的大小。 min为整型最大值,用于记录…...
)
MySQL表的基础操作(crud)
1. 新增(Create) insert into 表名 values (值, 值…); 此处列出的这些值,的数目和类型要和表的列相匹配。 -- 在student 表中插入学号1,姓名zhangsan的数据 insert into student values(1, zhangsan); -- 指定列插入 insert into student …...

vue中的activated和deactivated
目录 一、简介二、使用 一、简介 当页面被keep-alive缓存下来的时候,vue提供两个钩子函数 activated被 keep-alive 缓存的组件激活时调用。deactivated被 keep-alive 缓存的组件失活时调用。 当keepalive页面缓存,有activated钩子和created钩子函数时 …...

unity 发布报错 The type or namespace name `UnityEditor‘ could not be found.
引用了UnityEditor的内容,发布当然会报错啦 加上宏判断就好啦...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
