算法竞赛备赛之搜索与图论训练提升,暑期集训营培训

目录
1.DFS和BFS
1.1.DFS深度优先搜索
1.2.BFS广度优先搜索
2.树与图的遍历:拓扑排序
3.最短路
3.1.迪杰斯特拉算法
3.2.贝尔曼算法
3.3.SPFA算法
3.4.多源汇最短路Floy算法
4.最小生成树
4.1.普利姆算法
4.2.克鲁斯卡尔算法
5.二分图:染色法,匈牙利算法
5.1.染色法
5.2.匈牙利算法
1.DFS和BFS
1.1.DFS深度优先搜索
深度优先搜索(Depth-First Search, DFS)是一种用于遍历或搜索树或图的算法。它从起点开始,沿着一个路径一直到达最深的节点,然后回溯到之前的节点,继续探索下一个路径,直到所有的节点都被访问过。
DFS使用一个栈来存储待访问的节点,它会将起点压入栈中,然后重复执行以下步骤直到栈为空:
-
弹出栈顶节点。
-
如果该节点是目标节点,则搜索结束。
-
否则将该节点标记为已访问,并将其所有未访问的邻居节点按照某种规则(如按字母表顺序)依次压入栈中。
使用DFS的优点是它的空间复杂度相对较小,因为它只需要存储一条路径上的节点。但是,如果搜索的图或树非常大,DFS可能会陷入死循环或者长时间运行。此外,DFS不一定能找到最优解,因为它只探索了一条路径,而不是所有可能的路径。
因此,在实际应用中,需要根据具体问题的要求选择合适的搜索算法。例如,如果需要找到最短路径,可能更适合使用广度优先搜索(Breadth-First Search, BFS)算法。
842.排列数字:
给定一个整数n,将数字1~n排成一排,将会有很多排列方法。
现在,请你按照字典序将所有的排列方法输出。
#include<iostream>
using namespace std;
const int N = 7;
int n;
int path[N];
bool st[N];
void dfs(int u)
{if(u == n){for(int i = 0;i < n; i++)printf("%d ", path[i]);printf("\n");return;}for(int i = 1;i <= n; i++){if(!st[i]){path[u] = i;st[i] = true;dfs(u+1);st[i] = false;}}
}
int main()
{scanf("%d", &n);dfs(0);return 0;
}843.n-皇后问题:
n-皇后问题是指将n个皇后放在n-n的国际棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数n,请你输出所有的满足条件的棋盘摆法。
法1
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u)
{if(u == n){for(int i = 0;i < n; i++)puts(g[i]);printf("\n");return;}fot(int i = 1;i <= n; i++){if(!col[i] && !dg[u + i] && !udg[n - u + i]){path[u] = i;col[i] = dg[u + i] = udg[n - u + i] = true;dfs(u+1);col[i] = dg[u + i] = udg[n - u + i] = false;g[u][i] = '·';}}
}
int main()
{scanf("%d", &n);for(int i = 0;i < n; i++){for(int j = 0;j < n; j++)g[i][j] = '·';}dfs(0);return 0;
}法2:
#include<iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N * 2], udg[N * 2];
void dfs(int x, int y, int s)
{if(y == n){y = 0;x++;}if(x == n){if(s == n){for(int i = 0;i < n; i++)puts(g[i]);puts("");}return;}//不放皇后dfs(x, y+1, s);//放皇后if(!row[x] && !col[y] && !dg[x+y] && !udg[x-y+n]){g[x][y] = 'Q';row[x] = col[y] = dg[x+y] = udg[x-y+n] = true;dfs(x, y+1, s+1);row[x] = col[y] = dg[x+y] = udg[x-y+n] = false;g[x][y] = '.';}
}
int main()
{scanf("%d", &n);for(int i = 0;i < n; i++){for(int j = 0;j < n; j++){g[i][j] = '.';}}dfs(0, 0, 0);return 0;
}1.2.BFS广度优先搜索
广度优先搜索(Breadth-First Search, BFS)是一种用于遍历或搜索树或图的算法。它从起点开始,首先访问所有与起点直接相邻的节点,然后访问这些节点的相邻节点,以此类推,直到所有的节点都被访问过。
BFS使用一个队列来存储待访问的节点,它会将起点压入队列中,然后重复执行以下步骤直到队列为空:
-
弹出队列首部节点。
-
如果该节点是目标节点,则搜索结束。
-
否则将该节点标记为已访问,并将其所有未访问的邻居节点按照某种规则(如按字母表顺序)依次压入队列中。
使用BFS的优点是它能够保证在最少的时间内找到目标节点,因为它是按照距离从起点由近到远进行搜索的。此外,BFS也能够处理有向无环图(DAG)和图的情况。但是,如果搜索的图或树非常大,BFS可能需要较大的空间来存储队列中的节点,因此空间复杂度较大。
因此,在实际应用中,需要根据具体问题的要求选择合适的搜索算法。例如,如果需要找到深度优先搜索的最短路径,可能更适合使用深度优先搜索算法。
844.走迷宫:
给定一个n*m的二维整数数组,用来表示一个迷宫,数组中只包含0成1,其中0表示可以走的路,表示不可通过的墙壁。最初,有一个人位于左上角(1, 1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角(n, m)处,至少需要移动多少次。
数据保证(1, 1)处和(n, m)处的数字为0,且一定至少存在1条通路。
程序代码1:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int g[N][N];
int d[N][N];
int n, m;
int bfs()
{queue<pair<int, int>> q;q.push({0, 0});memset(d, -1, sizeof(d));d[0][0] = 0;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while(q.size()){PII t = q.front();q.pop();for(int i = 0;i < 4; i++){int x = t.first + dx[i], y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;q.push({x, y});}}}return d[n-1][m-1];
}
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < n; i++)for(int j = 0;j < m; j++)scanf("%d", &g[i][j]);cout << bfs() << endl;return 0;
}打印路径代码:
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n, m;
int g[N][N];
int d[N][N];
int prev[N][N];
PII q[N * N];
int bfs()
{int hh = 0, tt = 0;q[0] = {0, 0};memset(d, -1, sizeof(d));d[0][0] = 0;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while(hh <= tt){auto t = q[hh++];for(int i = 0;i < 4; i++){int x = t.first + dx[i], y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;prev[x][y] = t;q[++tt] = {x, y};}}}int x = n - 1, y = m - 1;while(x || y){cout << x << ' ' << y << endl;auto t = prev[x][y];x = t.first, y = t.second;}return d[n-1][m-1];
}
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < n; i++){for(int j = 0;j < m; j++){scanf("%d", g[i][j]);}}cout << bfs() << endl;return 0;
}5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
八数码
树是一种特殊的图,属于无环图。
图分为有向图和无向图。
846.树的重心:
给定一棵树,树中包含n个结点(编号1~n)和n-1条无向边。
请你找出树的重心,并输出将重心删除后剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个节点,如果将这个结点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
代码:
#include<iostream>
using namespace std;
const int N = 100010, M = N * 2;
int n, m;
int h[N], e[M], ne[M], idx;
bool st[N];
int ans = N;
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
int dfs(int u)
{st[u] = true;//标记一下int sum = 0, res = 0;for(int i = h[u];i != -1; i = ne[i]){int j = e[i];if(!st[j]){int s = dfs(j);res = max(res, s);sum += s;}}res = max(res, n - sum - 1);ans = min(ans, res);return sum + 1;
}
int main()
{scanf("%d", &n);memset(h, -1, sizeof(h));for(int i = 0;i < n - 1; i++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}847.图中点的层次:
给定一个n个点m条边的有向图,图中可能存在重边和自环。
所有边的长度都是1,点的编号为1~n。
请你求出1号点到n点的最短距离,如果从1号点无法走到n号点,输出-1。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
int bfs()
{int hh = 0, tt = 0;q[0] = 1;memset(d, -1, sizeof(d));d[1] = 0;while(hh <= tt){int t = q[hh++];for(int i = h[t];i != -1; i = ne[i]){int j = e[i];if(d[j] == -1){d[j] = d[t] + 1;q[++tt] = j;}}}return d[n];
}
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0;i < m; i++){int a, b;cin >> a >> b;add(a, b);}cout << bfs() << endl;return 0;
}2.树与图的遍历:拓扑排序
848.有向图的拓扑序列
给定一个n个点m条边的有向图,图中可能存在重边和自环。
请输入任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出-1.
若一个由图中所有点构成的序列A满足:对于图中的每一条边(x, y),x在A中都有出现在y之前,则称A是该图的一个拓扑序列。
有向无环图——拓扑图
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool topsort()
{int hh = 0, tt = 0;for(int i = 1;i <= n; i++){if(!d[i])q[++tt] = i;}while(hh <= tt){int t = q[hh++];for(int i = h[t];i != -1; i = ne[i]){int j = e[t];d[j]--;if(d[j] == 0){q[++tt] = j;}}}return tt == n - 1;
}
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0;i < n; i++){int a, b;cin >> a >> b;add(a, b);d[b]++;}if(topsort()){for(int i = 0;i < n; i++)printf("%d ", q[i]);puts("");}elseputs("-1");cout << << endl;return 0;
}3.最短路
最短路问题是在给定的有向图或无向图中找到从起点到终点的最短路径的问题。这个问题在计算机科学和应用数学中有着广泛的应用,例如在路由算法、交通控制和电路设计中都需要解决最短路问题。
解决最短路问题的方法主要有两种:Dijkstra算法和Bellman-Ford算法。
Dijkstra算法是一种贪心算法,它基于图论的原理,通过不断更新起点到各个节点的最短距离,最终求得起点到终点的最短路径。该算法的基本思路是从起点开始,每次选择一个距离起点最近的节点,并更新起点到各个节点的距离。通过不断重复这个过程,最终可以得到起点到终点的最短路径。
Bellman-Ford算法是一种动态规划算法,它可以处理带有负权边的图。该算法的基本思路是通过对所有节点进行多次松弛操作,逐步更新起点到各个节点的最短距离。在每次松弛操作中,该算法会检查是否存在一个节点的距离可以通过其他节点的路径得到更短的距离,如果有,则更新该节点的距离。通过多次松弛操作,该算法可以找到起点到终点的最短路径。
除了这两种算法,还有其他一些解决最短路问题的方法,例如Floyd-Warshall算法和A*算法等。不同的算法适用于不同类型的图和不同的应用场景,需要根据具体情况选择合适的算法。
3.1.迪杰斯特拉算法
Dijkstra算法是一种用于解决最短路径问题的算法,它可以在带权重的图中找到从一个起点到所有其他节点的最短路径。
该算法的基本思路是从起点开始,每次选择距离最短的节点作为中转点,并将该节点的邻居节点更新距离,直到所有节点都被访问过或者没有可达的节点。
具体实现过程如下:
-
初始化:将起点的距离设置为0,其他节点的距离设置为无穷大。
-
选择中转点:从起点开始,选择距离起点最近的节点作为中转点,将该节点的距离更新为起点到该节点的距离。
-
更新距离:对于中转点周围的邻居节点,如果从起点到该邻居节点的距离比之前的距离更短,则更新该邻居节点的距离为起点到该邻居节点的距离。
-
重复步骤2和步骤3,直到所有节点都被访问过或者没有可达的节点。
-
输出结果:最终得到从起点到所有节点的最短路径。
Dijkstra算法的时间复杂度为O(n^2),其中n是节点的数量。如果使用堆优化可以将时间复杂度优化为O(m log n),其中m是边数。
849.Dijkstra求最短路I:
给定一个n个点m条边的1有向图,图中可能存在重边和自环,所以边权均为正值。
请你求出1号点到n号点的最短距离,如果无法从1号点走到n号点,则输出-1.
3 3
1 2 2
2 3 1
1 3 4
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;
int n, m;
int g[N][N];
int dist[N][N];
bool st[N];
int dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 0;i < n; i++){int t = -1;for(int j = 1;j <= n; j++)if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;st[t] = true;for(int j = 1;j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]); }if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
int main()
{cin >> n >> m;memset(g, 0x3f, sizeof(g));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c);}int t = dijkstra();printf("%d\n", t);return 0;
}Dijkstra求最小短路II:
堆优化版dijkstra算法
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
int dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;if(st[ver]) continue;for(int i = h[ver];i != -1; i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = dijkstra();printf("%d\n", t);return 0;
}3.2.贝尔曼算法
Bellman-Ford算法
for循环n次,每一次循环所有边
dist[b] = min(dist[b], dist[a]) 松弛操作
dist[b] ≤ dist[a] + w三角不等式 有负权边就很难成立啦
853.有边数限制的最短路:
给定一个n个点m条边的有向图,图中可能存在重边和自环,边权可能为负数。
请你求出从1号点到n号点的最多经过k条边的最短距离,如果无法从1号点走到n号点,输出impossible。
注意:图中可能存在负权回路。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510, M = 10010;
int n, m, k;
iny dist[N], backup[N];
struct Edge
{int a, b, w;
}edges[M];
int bellman_ford()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;for(int i = 0;i < k; i++){memcpy(bakcup, dist, sizeof(backup));for(int j = 0;j < m; j++){int a = edges[j].a, b = edges[i].b, w = edges[i].w;dist[b] = min(dist[b], backup[a] + w);}}if(dist[n] > 0x3f3f3f3f / 2) return -1;return dist[n];
}
int main()
{scanf("%d%d%d", &n, &m, &k);for(int i = 0;i < m; i++){int a, b, w;scanf("%d%d%d", &a, &b, &w);edges[i] = {a, b, w};}int t = bellman_ford();if(t == -1)puts("impossible");else printf("%d\n", t);return 0;
}3.3.SPFA算法
851.spfa求最短路
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 510, M = 10010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
int spfa()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;queue<int> q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){q.push(j);st[j] = true;}}}}if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
int main()
{scanf("%d%d%d", &a, &b, &c);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = spfa();if(t == -1)puts("");elseprintf("%d\n", t);return 0;
}852.spfa判断负环:
给定一个n个点m条边的有向图,图中可能存在重边和自环,边权可能为负数。
请你判断图中是否存在负权回路。
3 3
1 2 -1
2 3 4
3 1 -4
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 10010;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
int spfa()
{queue<int> q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i = h[t];i != -1;i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] >= n) return true;if((!st[j])){q.push(j);st[j] = true;}}}}return false;
}
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}if(spaf())printf("Yes\n");elseprintf("No\n");return 0;
}3.4.多源汇最短路Floy算法
for(int k = 1;k <= n; k++)
{for(i = 1;i <= n; i++){for(int j = 1;j <= n; j++){d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}
}
854.Floyd求最短路:
给定一个n个点m条边的有向图,图中可能存在重边和闭环,边权可能为负数。
再给定k个询问,每个询问包含两个整数x和y,表示查询从点x到点y的最短距离,如果路径不存在,则输出“impossible”
数据保证图中不存在负权回路。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e4 + 10;
int n, m, Q;
int d[N][N];
void floyd()
{for(int k = 1;k <= n; k++){for(int i = 1;i <= n; i++){for(int j = 1;j <= n; j++){d[i][j] = min(d[i][k], d[k][j]);}}}
}
int main()
{scanf("%d%d%d", &n, &m, &Q);for(int i = 1;i <= n; i++){for(int j = 1;j <= n; j++){if(i == j)d[i][j] = 0;elsed[i][j] = INF;}}while(m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);d[a][b] = min(d[a][b], w);}floyd();while(Q--){int a, b;scanf("%d%d",&a, &b);if(d[a][b] == INF)puts("impossible");elseprintf("%d\n", d[a][b]);}return 0;
}4.最小生成树
最小生成树的两个算法:
-
普利姆算法(Prim)
-
克鲁斯卡尔算法(Kruskal)
4.1.普利姆算法
朴素版Prim,类似于Dijkstra算法
Dijkstra算法的主体部分:
int dijkstra()
{memset(dist, -1, sizeof(dist));dist[1] = 0;for(int i = 0;i < n - 1; i++){int t = -1;for(int j = 1;j <= n; j++){if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;}for(int j = 1;j <= n; j++){dist[j] = min(dist[j], dist[t] + g[t][j]);}st[t] = true;}if(dist[n] == 0x3f3f3f3f)return -1;return dist[n];
}
prim的算法思路
dist[i] <- 正无穷
for(i = 0;i < n; i++) {t->找到集合距离最近的点用t更新其他点到集合的距离,st[t] = true; }
858.Prim算法求最小生成树:
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负。
求最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=[V],m=[E]
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和和最小的生成树被称为无向图G的最小连通图。
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
cosnt int N = 1e4 + 10;
int n, m;
int g[N][N];
int dist[N];
bool st[N];
int prim()
{memset(dist, 0x3f, sizeof(dist));int res = 0;for(int i = 0;i < n; i++){int t = -1;for(int j = 1;j <= n; j++){if(!st[t] && (t == -1 || dist[t] > dist[j]))t = j;if(i && dist[t] == INF)return INF;if(i)res += dist[t];for(int j = 1;j <= n; j++)dist[j] = min(dist[j], g[t][j]);st[t] = true;}}return true;
}
int main()
{scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof(g));while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}int t = prim();if(t == INF)puts("impossible");elseprintf("%d\n", t);return 0;
}堆优化版Prim
竞赛中实际上用到的不多。
4.2.克鲁斯卡尔算法
Kruskal算法的基本思想:
-
将所有边按照权重从小到大排序
-
枚举每条边a,b,权重c 如果a,b不连通,就将这条边加入到这个集合里面
859.Kruskal算法求最小生成树:
4 5
1 2 1
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e4 + 10;
int n, m;
int p[N];
struct Edge
{int a, b, w;bool operator< (const Edge &W)const{return w < W.w;}
}edges[N];
int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];}
int main()
{scanf("%d%d", &n, &m);for(int i = 0;i < m; i++){int a, b, c;scanf("%d%d%d", &a, &b, &c);edges[i] = {a, b, w};}sort(edges, edges + m);for(int i = 1;i <= n; i++)p[i] = i;int res = 0, cnt = 0;for(int i = 0;i < m; i++){int a = edges[i].a, b = edges[i].b, w = edges[i].w;a = find(a), b = find(b);if(a != b){p[a] = b;res += w;cnt++;}}if(cnt < n - 1)puts("impossible");elseprintf("%d\n", res);return 0;
}5.二分图:染色法,匈牙利算法
二分图当且仅当图中不含奇数环。
二分图又叫二部图,是图论中的一种特殊模型。设G=(V,E)是无向图,如果根据顶点V可分割为两个互不相交的子集(A,B),且图中的每条边(i,j)所关联的两个顶点i和j分属这两个不同的顶点集(i∈A,j∈B),则图G就是一个二分图。简单来说,就是顶点集V可分割为两个互不相交的子集,且图中每条边依附的两个顶点都分属于这两个互不相交的子集,两个子集内的顶点不相邻。
二分图有最大匹配和最小匹配问题,在二分图中的一个匹配是指边集中任意两条边都不依附于同一个顶点,极大匹配是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数,最大匹配是所有极大匹配当中边数最大的一个匹配。
分辨是否是二分图:
-
染色法 O(n + m)
-
匈牙利算法 O(mn),实际运行时间一般远小于O(mn)
5.1.染色法
二分图染色法是一种判断二分图的方法,可以分为连通图判断和非连通图判断1。
染色思路如下:
-
初始所有顶点未染色。
-
随意取出一个未染色的顶点u,把它染成一种颜色(假设为0)。
-
取与它连接的结点v,如果v未染色,则将v染成和u不同的颜色(假设为1),如果v已经染色,那么判断u和v颜色是否相同,相同则表明染色失败,该图不是二分图,结束。
-
遍历所有结点,重复步骤)。
-
连通图只需要一次dfs染色,非连通图则多次dfs染色。
for(int i = 1;i <= n; i++)
{if(v未染色)dfs(i);
}
860.染色法判定二分图
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool dfs(int u, int father, int c)
{color[u] = c;for(int i = h[u];i != -1; i = ne[i]){int j = e[i];if(color[j] == -1){if(!dfs(j, 3 - c)) return false;}else if(color[j] == c) return false;}return true;
}
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof(h));while(m--){int a, b;scanf("%d%d", &a, &b);add(a, b), add(b, a);}bool flag = true;for(int i = 1;i <= n; i++){if(!color[i]){if(!dfs(i, 1)){flag = false;break;}}}if(flag) puts("Yes");else puts("No");return 0;
}题目:关押罪犯
5.2.匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法,并推动了后来的原始对偶方法。
861.二分图的最大匹配
给定一个二分图,其中左半部包含n1个点(编号1~n1),右半部包含n2个点(编号1 ~n2),二分图共包含m条边。
数据保证任意一条边的两个端点都不可能在同一个部分。
请你求出二分图的最大匹配数。
给定一个二分图G,在G的一个子图M中,M的边集(E)的任意两条边都不依附于同一个顶点,则称为一个匹配。
所有匹配中包含边数最多的一组匹配称为二分图的最大匹配数。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510, M = 1e5 + 10;
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool find(int x)
{for(int i = h[x];i != -1; i = ne[i]){int j = e[i];if(!st[j]){st[j] = true;if(match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}
int main()
{scanf("%d%d%d", &n1, &n2, &m);memset(h , -1, sizeof(h));while(m--){int a, b;scanf("%d%d", &a, &b);add(a, b);}int res = 0;for(int i = 1; i <= n1; i++){memset(st, false, sizeof(st));if(find(i)) res++;}printf("%d\n", res);return 0;
}2 2 4
1 1
1 2
2 1
2 2

相关文章:

算法竞赛备赛之搜索与图论训练提升,暑期集训营培训
目录 1.DFS和BFS 1.1.DFS深度优先搜索 1.2.BFS广度优先搜索 2.树与图的遍历:拓扑排序 3.最短路 3.1.迪杰斯特拉算法 3.2.贝尔曼算法 3.3.SPFA算法 3.4.多源汇最短路Floy算法 4.最小生成树 4.1.普利姆算法 4.2.克鲁斯卡尔算法 5.二分图:染色法…...
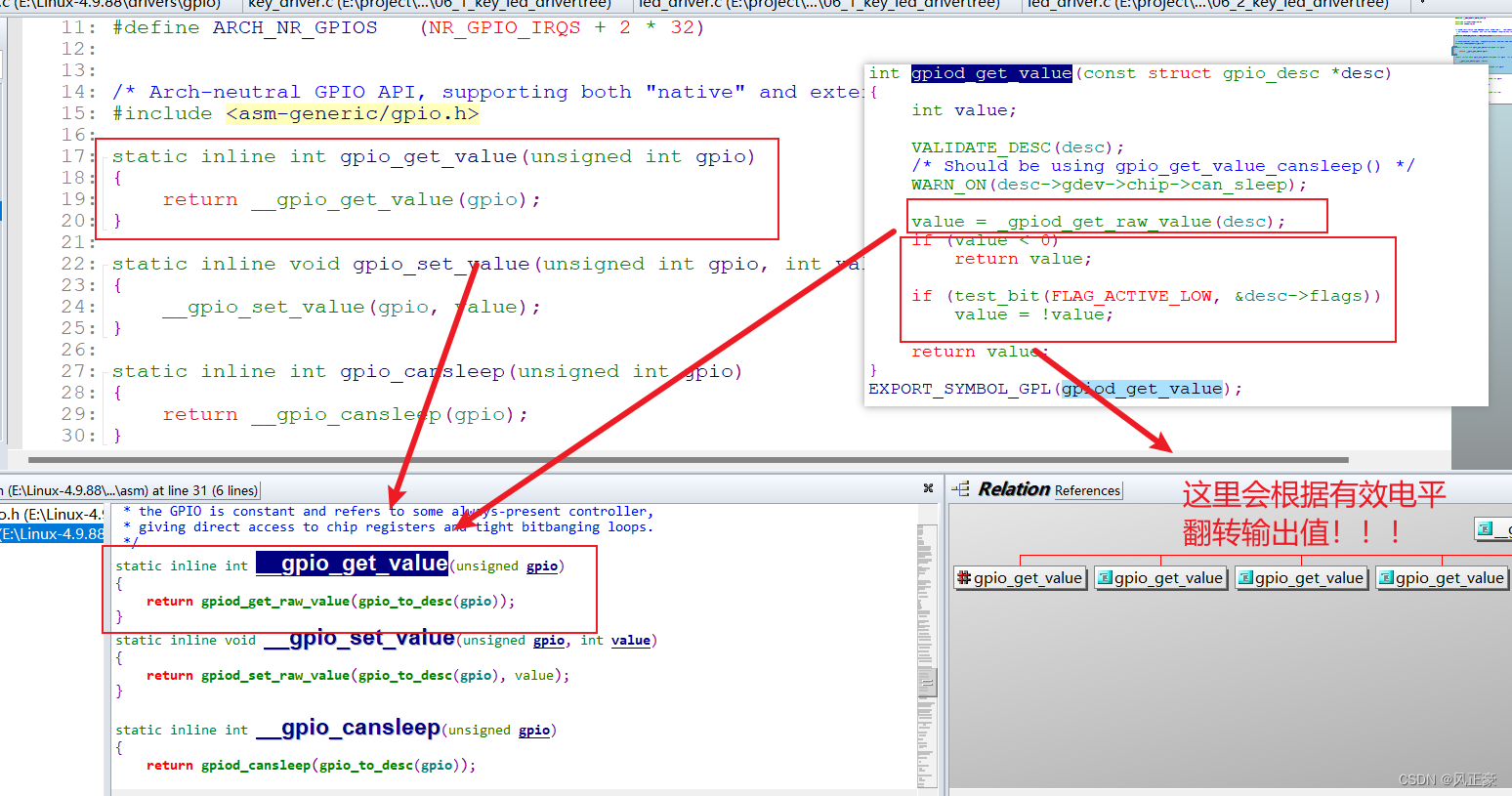
Linux驱动入门(6.2)按键驱动和LED驱动 --- 将逻辑电平与物理电平分离
前言 (1)在学习完Linux驱动入门(6)LED驱动—设备树之后,我们发现一个问题,设备树明明的gpios信息明明有三个元素gpios <&gpio5 3 GPIO_ACTIVE_LOW>; &gpio5 3 用来确定控制那个引脚…...
CentOS系统环境搭建(十四)——CentOS7.9安装elasticsearch-head
centos系统环境搭建专栏🔗点击跳转 关于node的安装请看上一篇CentOS系统环境搭建(十三)——CentOS7安装nvm,🔗点击跳转。 CentOS7.9安装elasticsearch-head 文章目录 CentOS7.9安装elasticsearch-head1.下载2.解压3.修…...
设计HTML5图像和多媒体
在网页中的文本信息直观、明了,而多媒体信息更富内涵和视觉冲击力。恰当使用不同类型的多媒体可以展示个性,突出重点,吸引用户。在HTML5之前,需要借助插件为网页添加多媒体,如Adobe Flash Player、苹果的QuickTime等。…...

基于YOLOv8模型和Caltech数据集的行人检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要 基于YOLOv8模型和Caltech数据集的行人检测系统可用于日常生活中检测与定位行人,利用深度学习算法可实现图片、视频、摄像头等方式的行人目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训练数据集…...

Flutter 宽高自适应
在Flutter开发中也需要宽高自适应,手动写一个工具类,集成之后在像素后面直接使用 px或者 rpx即可。 工具类代码如下: import dart:ui;class HYSizeFit {static double screenWidth 0.0;static double screenHeight 0.0;static double phys…...
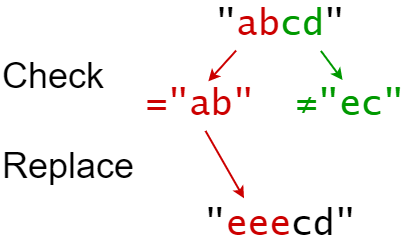
LeetCode 0833. 字符串中的查找与替换
【LetMeFly】833.字符串中的查找与替换 力扣题目链接:https://leetcode.cn/problems/find-and-replace-in-string/ 你会得到一个字符串 s (索引从 0 开始),你必须对它执行 k 个替换操作。替换操作以三个长度均为 k 的并行数组给出:indices,…...
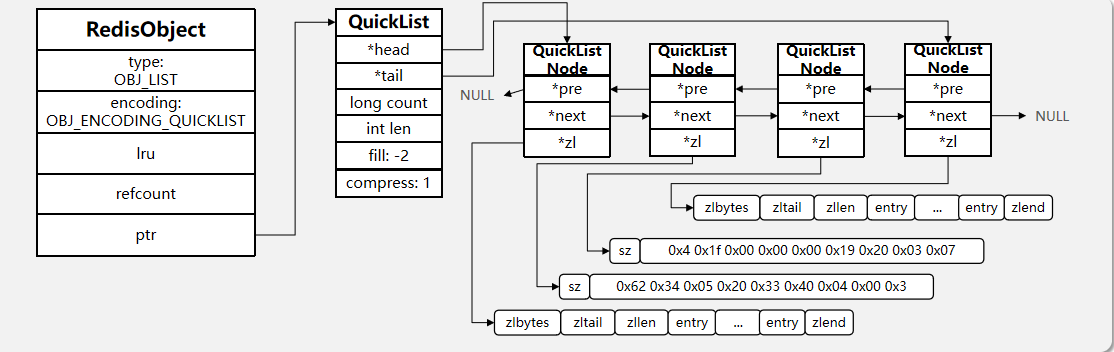
Redis对象和五种常用数据类型
Redisobject 对象 对象分为键对象和值对象 键对象一般是string类型 值对象可以是string,list,set,zset,hash q:redisobj的结构 typedef struct redisObject { //类型 unsigned type:4; //编码 unsigned encoding:4; //指向底层实现…...

常用的Elasticsearch查询DSL
1.基本查询 GET /index_name/_search {"query": {"match": {"dispatchClass": "1"}} }2.多条件查询 GET /index_name/_search {"query": {"bool": {"must": [{"match": {"createUser&…...

计算机网络笔记
TCP有连接可靠服务 TCP特点: 1.TCP是面向连接的传输层协议; 2.每条TCP连接只能有两个端点,每条TCP连接是一对一的; 3.TCP提供可靠交付,保证传送数据无差错,不丢失,不重复且有序; 4.…...
高效反编译luac文件
对于游戏开发人员,有时候希望从一些游戏apk中反编译出源代码,进行学习,但是如果你触碰到法律边缘,那么你要非常小心。 这篇文章,我针对一些用lua写客户端或者服务器的编译过的luac文件进行反编译,获取其源代码的过程。 这里我不赘述如何反编译解压apk包的过程了,只说重点…...

密码湘军,融合创新!麒麟信安参展2023商用密码大会,铸牢数据安全坚固堡垒
2023年8月9日至11日,商用密码大会在郑州国际会展中心正式开幕。本次大会由国家密码管理局指导,中国密码学会支持,郑州市人民政府、河南省密码管理局主办,以“密码赋能美好发展”为主题,旨在推进商用密码创新驱动、前沿…...
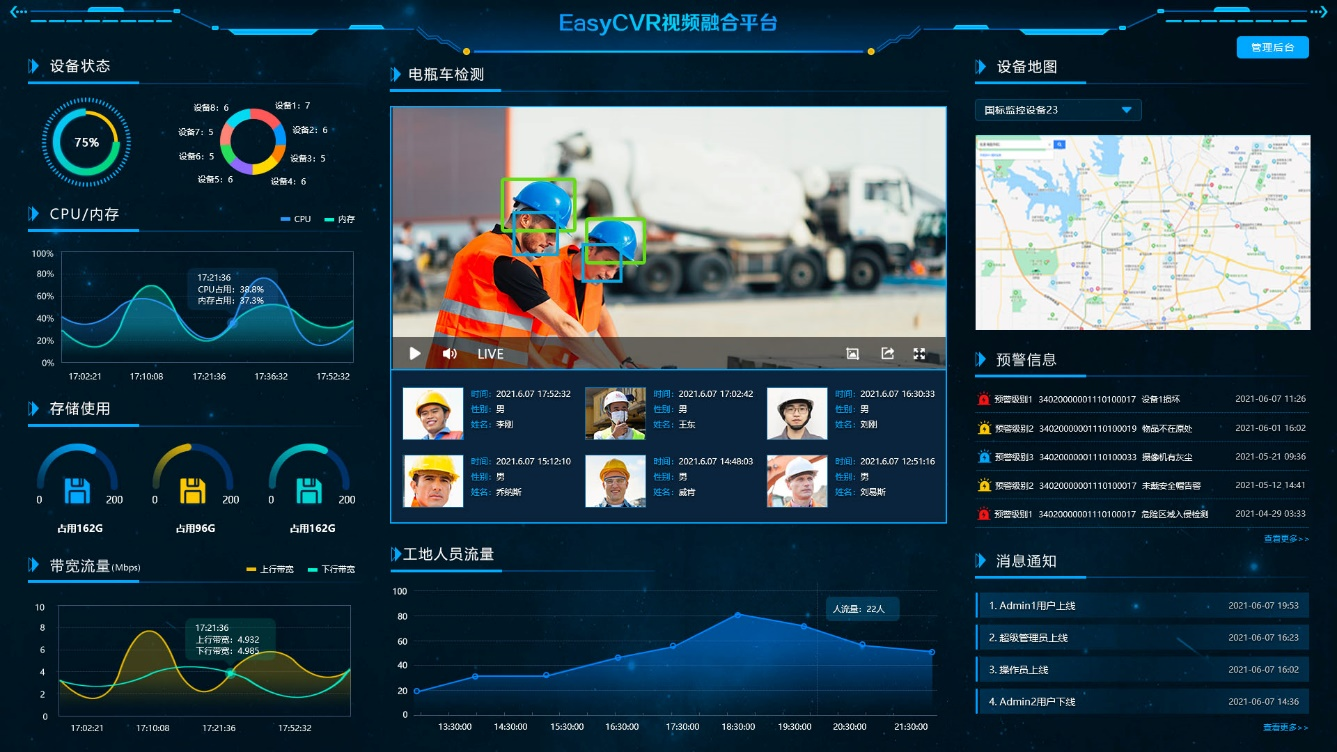
关于视频监控平台EasyCVR视频汇聚平台建设“明厨亮灶”具体实施方案以及应用
一、方案背景 近几年来,餐饮行业的食品安全、食品卫生等新闻频频发生,比如某火锅店、某网红奶茶,食材以次充好、后厨卫生被爆堪忧,种种问题引起大众关注和热议。这些负面新闻不仅让餐饮门店的品牌口碑暴跌,附带的连锁…...

区块链系统探索之路:私钥的压缩和WIF格式详解
在前面章节中,我们详细介绍了公钥的压缩,在比特币网络中,一个私钥可以对应两个地址,一个地址是由未压缩公钥所生成的地址,另一个就是由压缩公钥所创建的地址,从公钥到区块链地址的转换算法,我们…...

DiffusionDet: Diffusion Model for Object Detection
DiffusionDet: Diffusion Model for Object Detection 论文概述不同之处整体流程 论文题目:DiffusionDet: Diffusion Model for Object Detection 论文来源:arXiv preprint 2022 论文地址:https://arxiv.org/abs/2211.09788 论文代码…...

CH01_重构、第一个示例
概述 在这一章节,作者给出了一个戏剧演出团售票的示例:剧目有悲剧(tragedy)和喜剧(comedy);为了卖出更多的票,剧团则更具观众的数量来为下次演出打折扣(大致意思是这次的…...
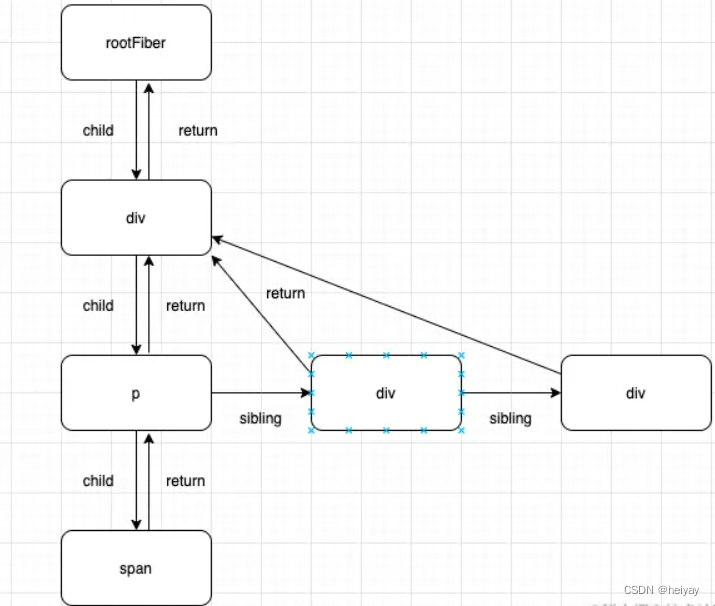
学习篇之React Fiber概念及原理
什么是React Fibber? React Fiber 是 React 框架的一种底层架构,为了改进 React 的渲染引擎,使其更加高效、灵活和可扩展。 传统上,React 使用一种称为堆栈调和递归算法来处理虚拟 DOM 的更新,这种方法在大型应用或者…...
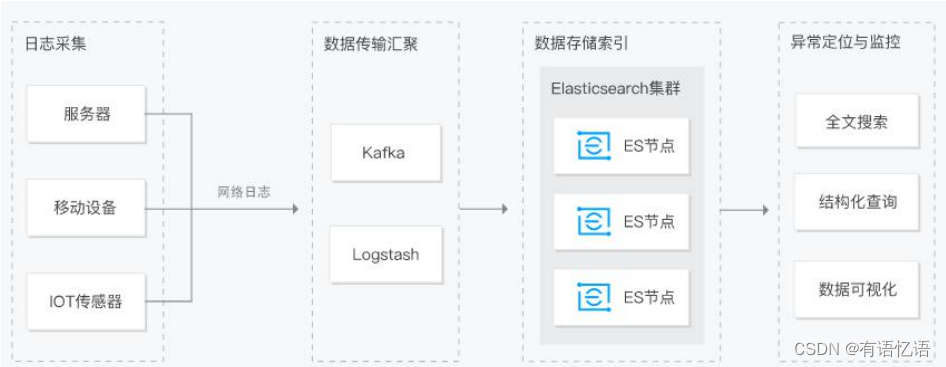
商城-学习整理-高级-全文检索-ES(九)
目录 一、ES简介1、网址2、基本概念1、Index(索引)2、Type(类型)3、Document(文档)4、倒排索引机制4.1 正向索引和倒排索引4.2 正向索引4.3 倒排索引 3、相关软件及下载地址3.1 Kibana简介3.2 logstash简介…...

无人机跟随一维高度避障场景--逻辑分析
无人机跟随一维高度避障场景--逻辑分析 1. 源由2. 视频3. 问题3.1 思维发散3.2 问题收敛 4. 图示4.1 水平模式4.2 下坡模式4.3 上坡模式4.4 碰撞分析 5. 总结5.1 一维高度避障场景5.2 业界跟随产品5.3 APM集成跟随 6. 参考资料7. 补充资料 - 大疆智能跟随7.1 炸机7.2 成功 1. 源…...
Android Studio Giraffe控制台乱码
这几天在使用Android Studio Giraffe进行一个App的开发,在项目构建的时候,控制台输出中文都是乱码,看着很不爽,进行了两项配置,中文就可以正常输出了,看起来就爽多了。 第一个配置:点击Help菜单…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
