【数据结构】树和二叉树
一、树的概念及结构
1、树的概念
- 有一个特殊的结点,称为根结点,根节点没有前驱结点。
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合 Ti (1<= i <= m) 又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
- 因此,树是递归定义的。
现实生活中的树: 数据结构中的树:


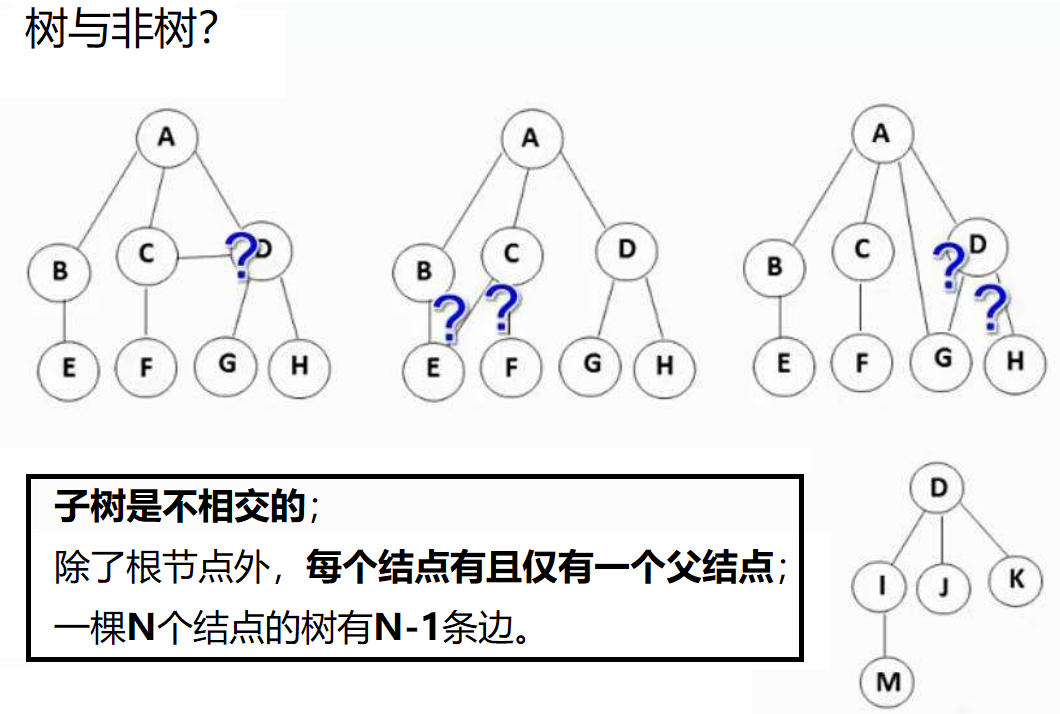
注意:树形结构中,子树之间不能有交集,否则就不是树形结构。
2、树的相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A 的度为 6。
- 叶节点或终端节点:度为 0 的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点。
- 非终端节点或分支节点:度不为 0 的节点; 如上图:D、E、F、G...等节点为分支节点。
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A 是 B 的父节点。
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C 是兄弟节点。
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为 6。
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第 2 层,以此类推。
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为 4。
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点。
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A 是所有节点的祖先。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是 A 的子孙。
- 森林:由m(m>0)棵互不相交的树的集合称为森林。
3、树的表示
树结构相对线性表比较复杂,要存储表示起来就比较麻烦。既然保存值域,也要保存结点和结点之间 的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
// 孩子兄弟表示法
typedef int DataType;
struct Node
{struct Node* firstChild1; // 第一个孩子结点struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域
};4、树在实际中的运用(表示文件系统的目录树结构)

二、二叉树的概念及结构
1、概念
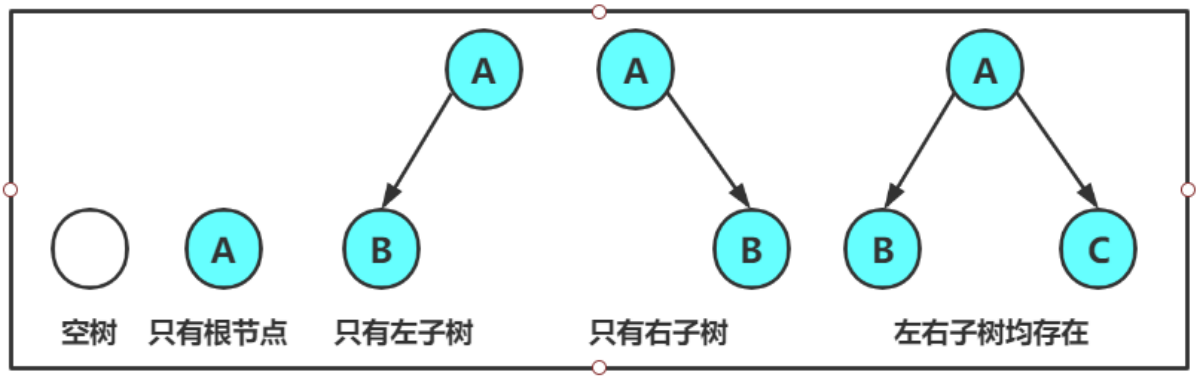
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
- 二叉树不存在度大于 2 的结点。
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
2、现实生活中的二叉树


3、特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 K,且结点总数是 2^K-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为 K 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。前 K 层都是满的,最后一层不一定满,但最后一层从左到右必须是连续的。深度为 K 的完全二叉树的节点个数最多为 2^K - 1,最少为 2^(K-1) - 1 + 1(前 K 层结点个数总和 +1,因为第 K 层至少有一个结点),所以节点个数范围是:[ 2K-1, 2K - 1 ]。
4、二叉树的性质
- 若规定根节点的层数为 1,则一棵非空二叉树的第 i 层上最多有 2^(i-1) 个结点。
- 若规定根节点的层数为 1,则深度为 h 的二叉树的最大结点数是 2^h-1。
- 对任何一棵二叉树, 如果度为 0 其叶结点个数为 n , 度为 2 的分支结点个数为 m ,则有 n= m+1。
- 若规定根节点的层数为 1,具有 n 个结点的满二叉树的深度,h= log(n+1). (ps:log(n+1)是 log 以 2 为底,n+1 为对数)。
- 对于具有 n 个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号,则对于序号为 i 的结点有:
- 若 i>0,i 位置节点的双亲序号:(i-1)/2;i=0,i 为根节点编号,无双亲节点。
- 若 2i+1<n,左孩子序号:2i+1,2i+1>=n 否则无左孩子。
- 若 2i+2<n,右孩子序号:2i+2,2i+2>=n 否则无右孩子。
5、二叉树的存储结构
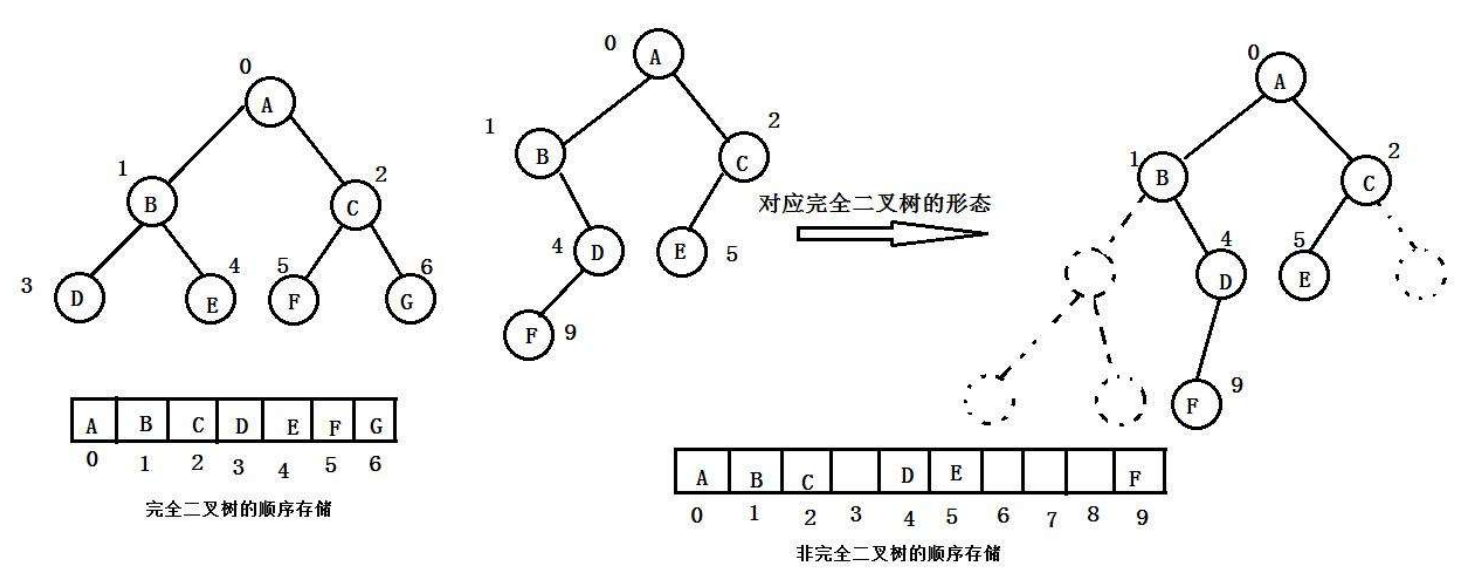
(1)顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树。因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
leftchild = parent * 2 + 1
rightchild = parent * 2 + 2
parent = (child - 1) / 2
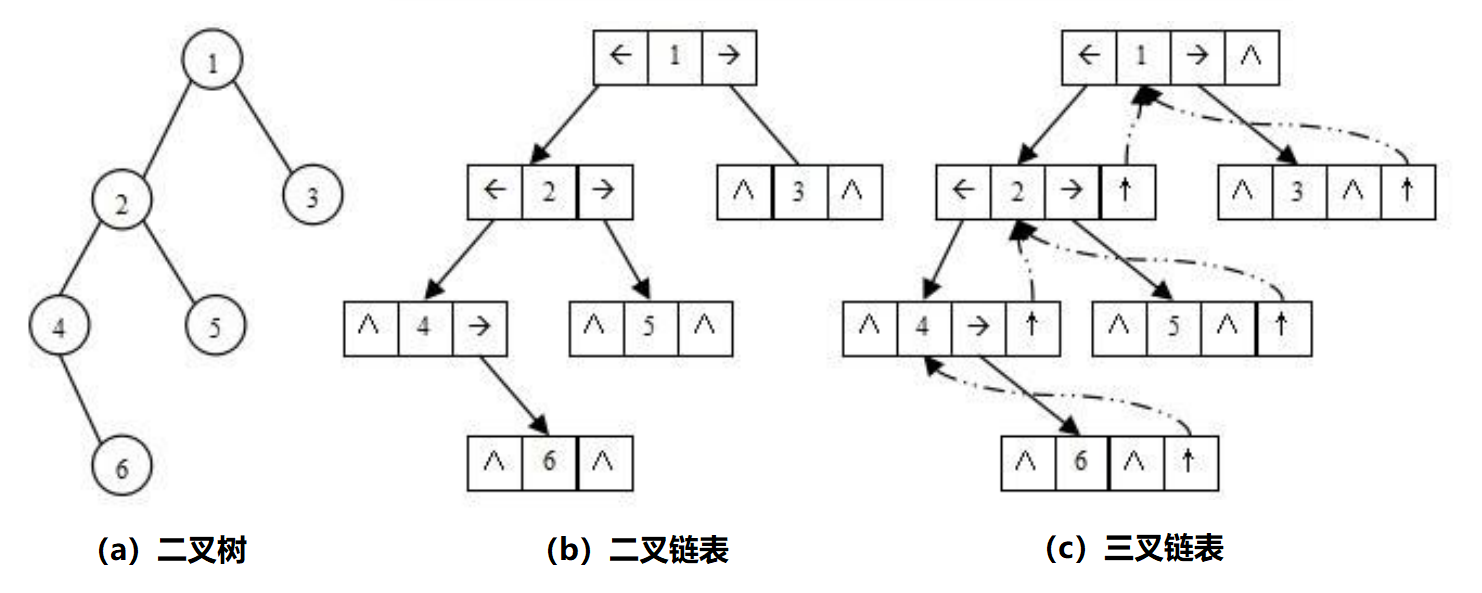
(2)链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链。目前我们一般用到的都是二叉链。( 后面的 数据结构内容如红黑树等会用到三叉链)
typedef int BTDataType;// 二叉链
struct BinaryTreeNode
{struct BinaryTreeNode* left; // 指向当前节点左孩子struct BinaryTreeNode* right; // 指向当前节点右孩子BTDataType data; // 当前节点值域
}// 三叉链
struct BinaryTreeNode
{struct BinaryTreeNode* parent; // 指向当前节点的双亲struct BinaryTreeNode* left; // 指向当前节点左孩子struct BinaryTreeNode* right; // 指向当前节点右孩子BTDataType data; // 当前节点值域
};相关文章:
【数据结构】树和二叉树
一、树的概念及结构 1、树的概念 树 是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点&a…...

GPIO 配置 和 PINCTRL有啥区别
GPIO(通用输入/输出)和 PINCTRL(引脚控制器)是在嵌入式系统中用于管理和控制硬件引脚的关键概念。它们在硬件层面上起着不同的作用。 GPIO配置: GPIO 是一种通用的硬件接口,用于控制和读取数字信号。每个 …...

GPT法律领域
法律领域 LaWGPT Github: https://github.com/pengxiao-song/LaWGPT 简介:基于中文法律知识的大语言模型。 数据:基于中文裁判文书网公开法律文书数据、司法考试数据等数据集展开,利用Stanford_alpaca、self-instruct方式生成对话问答数据…...
、alignof and alignas(类型对齐)))
【C++11保姆级教程】Type aliases(类型别名)、alignof and alignas(类型对齐))
文章目录 前言一、类型别名(Type aliases)1.1类型别名是什么?1.2使用方法1.3实际使用1.4优势 二、类型对齐(alignof and alignas)2.1类型对齐的概念2.2类型对齐快速理解2.3具体使用2.4示例代码 总结 前言 在C11标准中…...

地址解析协议-ARP
ARP协议 无论网络层使用何种协议,在实际网络的链路上传输数据帧时,最终必须使用硬件地址 地址解析协议(Address Resolution Protocol,ARP):完成IP地址到MAC地址的映射,每个主机都有一个ARP高速缓…...

Java线程
文章目录 一、Thread类1.1创建线程1.2Thread类中的一些构造方法1.3Thread类中的一些属性1.4线程的终止/打断1.5线程等待1.6获取当前线程的引用1.7休眠当前线程 二、线程的状态 一、Thread类 线程是操作系统的概念,操作系统内核实现了线程这样的机制,系统…...
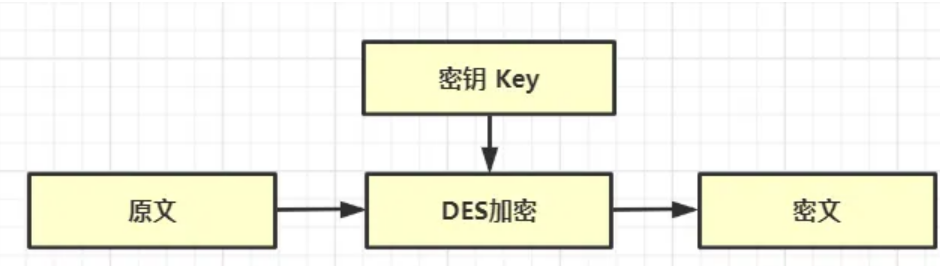
C语言如何实现DES加密与解密
C语言实现DES加密解密 #include "des.h" //移位表 static Table_size const shiftTable[NumberOfKeys] {1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1}; //E扩展表 static Table_size const eTable[des_key_pc2_standard]{32, 1, 2, 3, 4, 5, 4, 5, 6, …...
)
【笔记】优先队列(priority_queue/set)
目录 大根堆 小根堆 set(小根堆) 大根堆 题目链接:洛谷 P3243 菜肴制作 题目描述 知名美食家小 A 被邀请至 ATM 大酒店,为其品评菜肴。ATM 酒店为小 A 准备了 n 道菜肴,酒店按照为菜肴预估的质量从高到低给予 1 到…...
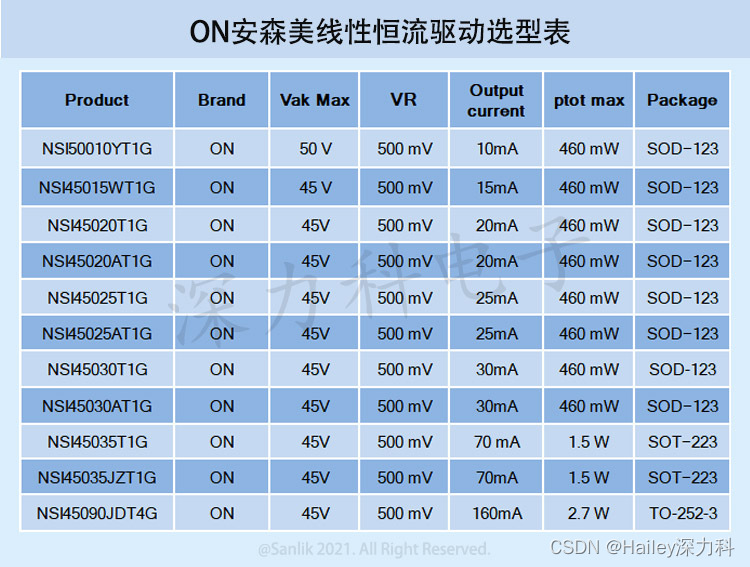
看看安森美深力科NSI45090JDT4G 是如何点亮汽车内外照明系统解决方案
关于线性恒流调节器(CCR):是一种用于控制电流的稳定输出。它通常由一个功率晶体管和一个参考电流源组成。CCR的工作原理是通过不断调节功率晶体管的导通时间来维持输出电流的恒定。当输出电流超过设定值时,CCR会减少功率晶体管的导…...

Linux进阶之Shell-sed
基本用法: sed 选项 “指令” 文件 常用选项: -e --它告诉sed将下一个参数解释为一个sed指令,只有当命令行上给出多个sed指令时使用 -f --后跟保存了sed指令的文件 -i --直接对内容进行修改,不加 i 时默认只是预…...

前端高频面试题 Day02
面试题 var 和 let const 的区别 var 是 ES5 及之前的语法,let const 是 ES6 语法var 和 let 是变量,可修改;const 是常量,不可修改var 有变量提升,let const 没有var 没有块级作用域,let const 有 &…...
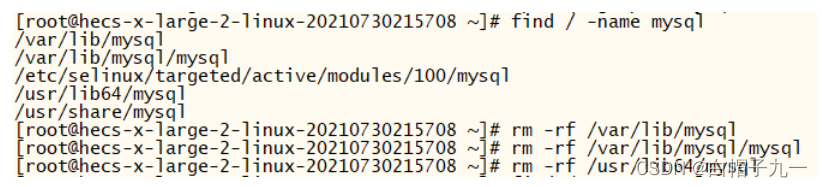
MYSQL完全卸载、安装与账号创建、权限控制
一、卸载mysql CentOS 卸载 MySQL 1. 查看安装情况 使用以下命令查看当前安装mysql情况,查找以前是否装有mysql rpm -qa|grep -i mysql这里显示我安装的 MySQL 服务有有: 2. 停止 mysql 服务、删除之前安装的 mysql 删除命令:rpm -e –n…...

get与post如何拼接url与数据的灵活处理,循环的重要性。
get与post拼接url地址不同: let postData {method: "post",data: {op: "/api/setting/maintenanceperiod?period"this.authorizationCode,loadingConfig: {},data: {period:this.authorizationCode}}}; if(this.editData.id){let postData …...
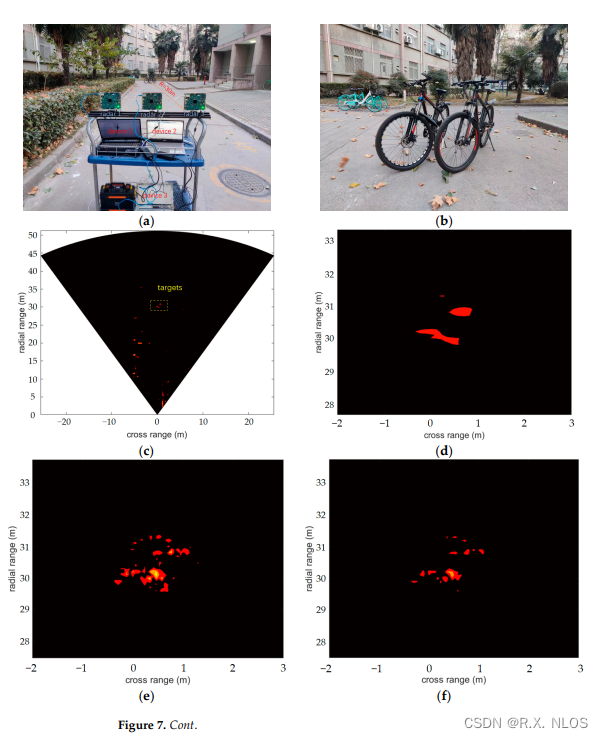
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现 注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI…...

Android学习之路(5) UI控件之Button (按钮)与 ImageButton (图像按钮)
本节引言: 今天给大家介绍的Android基本控件中的两个按钮控件,Button普通按钮和ImageButton图像按钮; 其实ImageButton和Button的用法基本类似,至于与图片相关的则和后面ImageView相同,所以本节 只对Button进行讲解&am…...
)
Day 31 C++ STL常用算法(下)
文章目录 常用拷贝和替换算法copy——容器内指定范围的元素拷贝到另一容器中函数原型注意——利用copy算法在拷贝时,目标容器要提前开辟空间示例 replace——将容器内指定范围的第一个旧元素修改为新元素函数原型注意——replace只会替换区间内满足条件的第一个旧元…...

【Android Studio】 win11 安装配置 jdk17 超详细
概述 一个好的安装教程能够帮助开发者完成更便捷、更快速的开发。书山有路勤为径,学海无涯苦作舟。我是秋知叶i、期望每一个阅读了我的文章的开发者都能够有所成长。 一、下载JDK JDK官网 这里下载 JDK17 windows x64 installer 二、安装JDK 双击打开下载的 j…...
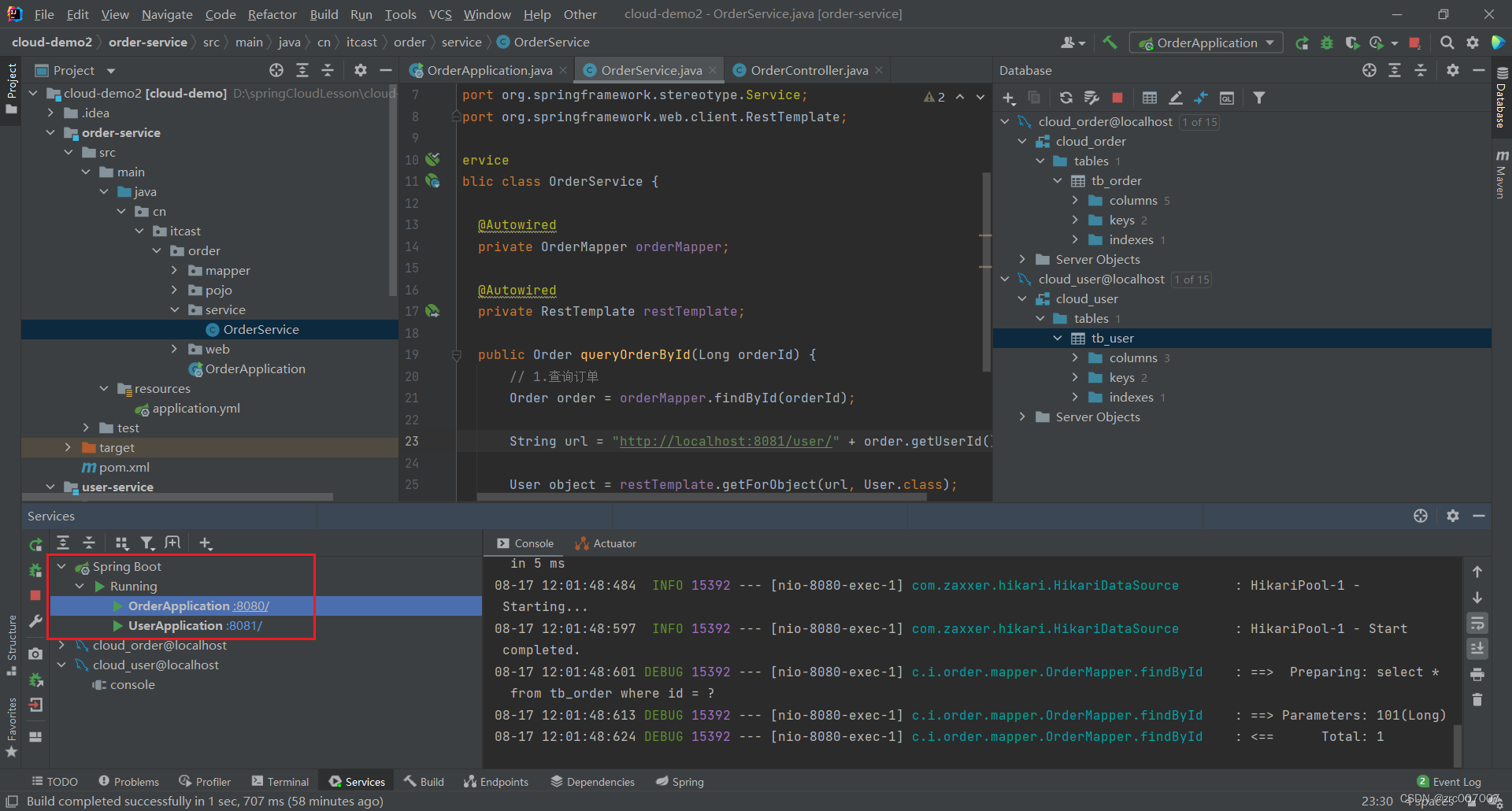
IDEA下方工具栏SideBar没有Services解决方法 IDEA配合微服务学习多端口管理打开Services栏方法
问题 微服务学习时,一次要打开多个端口,比如8080给order模块、8081给user模块……这就需要用idea管理多端口。 这时候就可以用到Services栏进行管理。 解决 首先看下方Sidebar没有Services。 打开Services 打开方式一:手动打开 在IDEA中…...

[Vue warn]: Error in render: “SyntaxError: “undefined“ is not valid JSON“
[Vue warn]: Error in render: “SyntaxError: “undefined” is not valid JSON” 这说明出现了undefined这个变量类型,比如JSON.parse()时候会出现,可以先尝试打印JSON.parse()括号中的内容是否是undefined,如果是,那问题的根源…...

ui设计师工作总结及计划范文模板
ui设计师工作总结及计划范文模板【篇一】 白驹过隙,转眼间某某年已近结尾,时间伴随着我们的脚步急驰而去,到了个人工作总结的时候,蓦然回首,才发现过去的一年不还能画上圆满的句号,内心感慨万千,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...