ARTS打卡:双指针的尝试
替换空格
<?php
class Solution {/*** @param String $s* @return String*/function replaceSpace($s) {$arr=str_split($s); //转化成数组foreach($arr as &$item){if($item==' '){//执行替换操作$item='%20';}}return implode('',$arr); //数组转化成字符串返回}
}反转链表
<?php
/*** Definition for a singly-linked list.* class ListNode {* public $val = 0;* public $next = null;* function __construct($val = 0, $next = null) {* $this->val = $val;* $this->next = $next;* }* }*/
class Solution {/*** @param ListNode $head* @return ListNode*/function reverseList($head) {$cur = $head;$pre = NULL;while($cur){$temp = $cur->next; $cur->next = $pre;$pre = $cur;$cur = $temp;}return $pre;}
}相关文章:

ARTS打卡:双指针的尝试
替换空格 <?php class Solution {/*** param String $s* return String*/function replaceSpace($s) {$arrstr_split($s); //转化成数组foreach($arr as &$item){if($item ){//执行替换操作$item%20;}}return implode(,$arr); //数组转化成字符串返回} } 反转链表…...
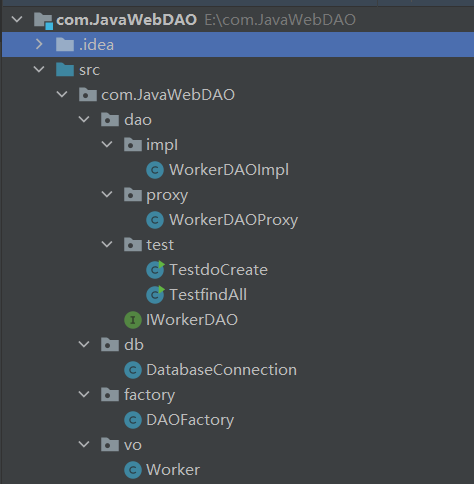
JavaWeb-DAO设计模式
目录 DAO设计模式 1.认识DAO 2.DAO各部分的详解 3.DAO设计模式流程 DAO设计模式 1.认识DAO DAO(Data Acess Object 数据库访问对象)的主要功能是操作数据库,所以DAO在标准开发架构中数据数据层,以下是标准开发的架构 客户层:目前使用B/…...

重温git和GitHub
1.初始化本地库:让git获取到这个目录的管理权 git init 查看文件夹的文件命令:ll 查看文件夹的隐藏的文件命令:ll -a 查看状态的命令:git status cat文件名:查看文件内容 工作区:当git status时,名字为红色则在工作区&…...
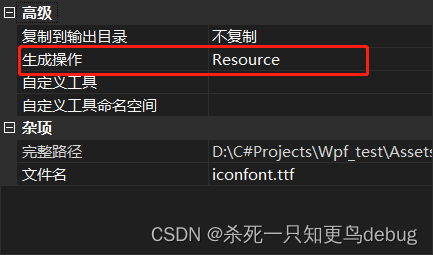
C# WPF 中 外部图标引入iconfont,无法正常显示问题 【小白记录】
wpf iconfont 外部图标引入,无法正常显示问题。 1. 检查资源路径和引入格式是否正确2. 检查资源是否包含在程序集中 1. 检查资源路径和引入格式是否正确 正确的格式,注意字体文件 “xxxx.ttf” 应写为 “#xxxx” <TextBlock Text"…...
Hi-TRS:骨架点视频序列的层级式建模及层级式自监督学习
论文题目:Hierarchically Self-Supervised Transformer for Human Skeleton Representation Learning 论文下载地址:https://www.ecva.net/papers/eccv_2022/papers_ECCV/papers/136860181.pdf 代码地址:https://github.com/yuxiaochen1103…...

FPGA 之 xilinx DDS IP相位控制字及频率控制字浅析
浅析相位环在Xilinx DDS中的理解 本文仅为个人理解之用; 相关仿真结果如下:...
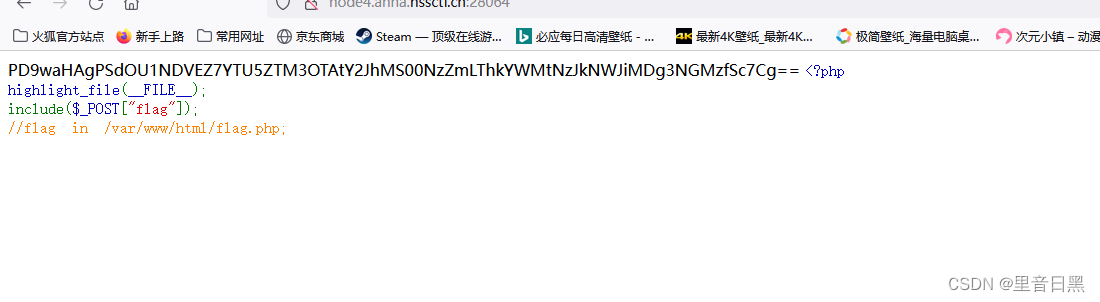
[鹏城杯 2022]简单包含
直接用php:// 有wtf 加脏数据绕过...

Required request parameter ‘XXX‘ for method parameter type XXX is not present问题
今日工作中遇到很奇葩的问题,用翻译软件翻译结果为 方法参数类型XXX所需的请求参数XXX不存在 也就是说前端没有给后端传值 后端的接收方式为 public Result demo(RequestParam("id") String id){}...

centOS 快速安装和配置 NVIDIA docker Container Toolkit
要在 CentOS 上正确安装和配置 NVIDIA Container Toolkit,您可以按照以下步骤进行操作,如果1和2都已经完成,可以直接进行第3步NVIDIA Container Toolkit安装配置。 1. 安装 NVIDIA GPU 驱动程序: 您可以从 NVIDIA 官方网站下载适…...
编程练习(2)
一.选择题 第一题: 考察转义字符和strlen函数求解字符串长度 进一步在VS中可以智能看出哪些字符是转义字符: 因此本体答案选择B 第二题: 本体较为简单,宏定义了三个数N,M,NUM,N值为2,M值为3,因此NUM值为8,…...
利用Figlet工具创建酷炫Linux Centos8服务器-登录欢迎界面-SHELL自动化编译安装代码
因为我们需要生成需要的特定字符,所以需要在当前服务器中安装Figlet,默认没有安装包的,其实如果我们也只要在一台环境中安装,然后需要什么字符只要复制到需要的服务器中,并不需要所有都安装。同样的,我们也可以利用此生成的字符用到脚本运行的开始起头部分,用ECHO分行标…...
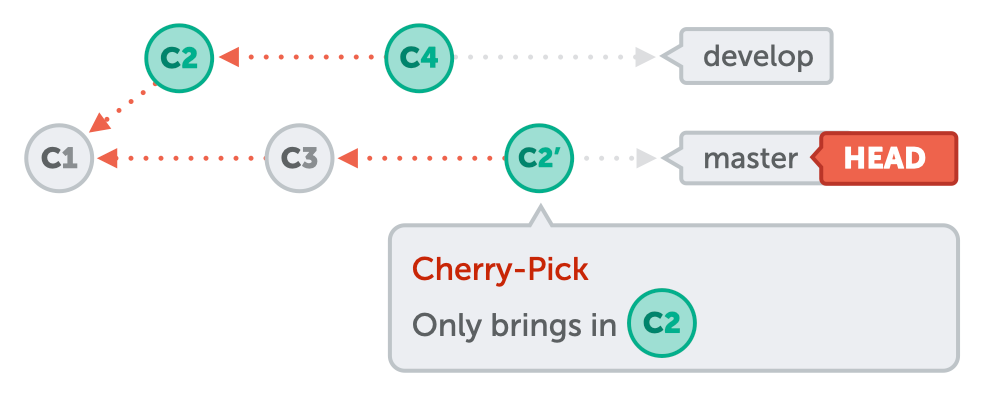
Git Cherry-pick使用
概述 无论项目大小,当你和一群程序员一起工作时,处理多个 Git 分支之间的变更都会变得很困难。有时,与其把整个 Git 分支合并到另一个分支,不如选择并移动几个特定的提交。这个过程被称为 "挑拣", 即 Cherry-pick。 本…...

红帽8.5 ansible 安装和部署 |(简单版)
什么是ansible Ansible是一款基于OpenSSH开源的自动化运维工具,可以用它来配置系统、部署软件和编排更高级的 IT 任务,并且使用具有极高的安全性,ansible是当前市面上主流的自动化运维工具之一 为什么使用ansible 比较直观的说,…...
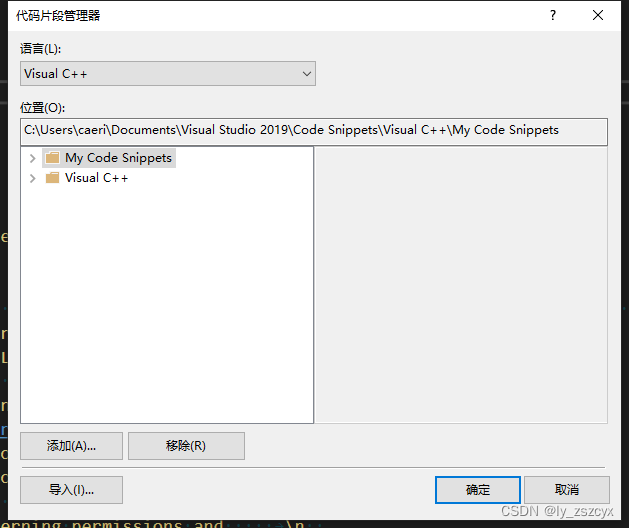
Visual Studio 2019 c++ 自定义注释 ----doxygen
可加入C 也可自定义。 <?xml version"1.0" encoding"utf-8"?> <CodeSnippets xmlns"http://schemas.microsoft.com/VisualStudio/2005/CodeSnippet"><CodeSnippet Format"1.0.0"><Header><Title>注释…...

面试题. 零矩阵
编写一种算法,若M N矩阵中某个元素为0,则将其所在的行与列清零。 示例 1: 输入: [[1,1,1],[1,0,1],[1,1,1] ] 输出: [[1,0,1],[0,0,0],[1,0,1] ] 示例 2: 输入: [[0,1,2,0],[3,4,5,2],[1,3…...

易语言下载器
静态网站整站下载器 https://bbs.125.la/forum.php?modviewthread&tid14791313&highlight%E4%B8%8B%E8%BD%BD%E5%99%A8 易语言 之音乐下载器 https://blog.51cto.com/u_15309652/3153642 (File Download Assistant)下载链接:https…...
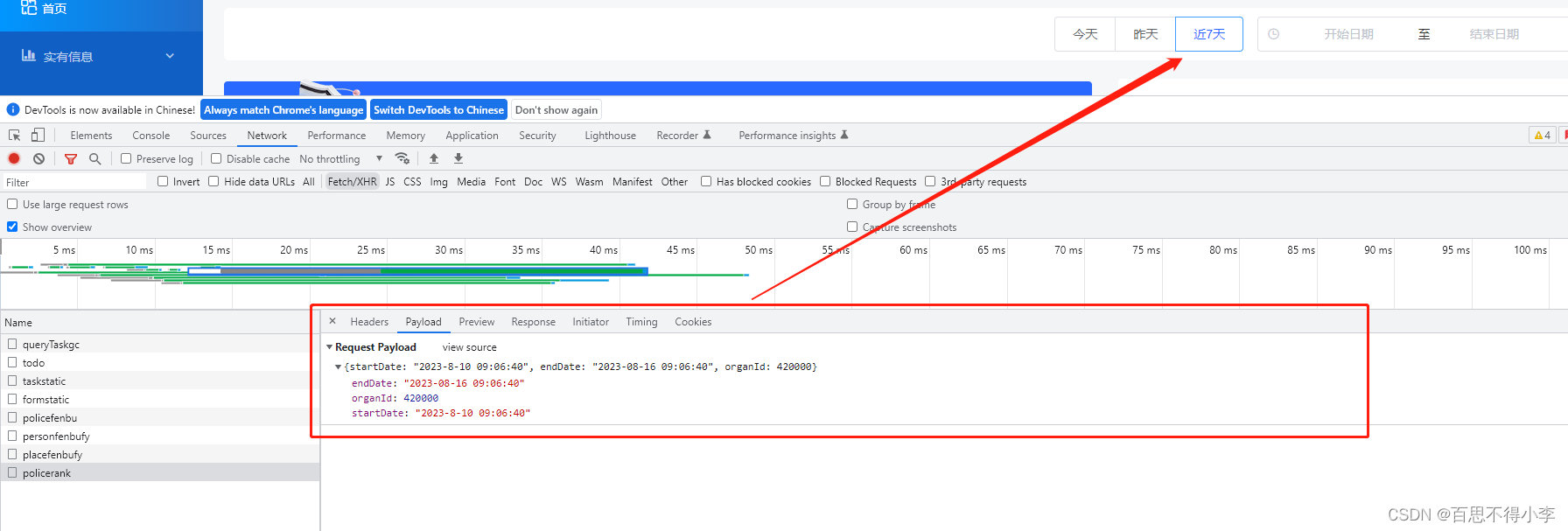
原生js获取今天、昨天、近7天的时间(年月日时分秒)
有的时候我们需要将今天,昨天,近7天的时间(年月日时分秒)作为参数传递给后端,如下图: 那怎么生成这些时间呢?如下代码里,在methods里的toDay方法、yesterDay方法、weekDay方法分别用于生成今天、昨天和近7天的时间: <template><div class="box"&…...
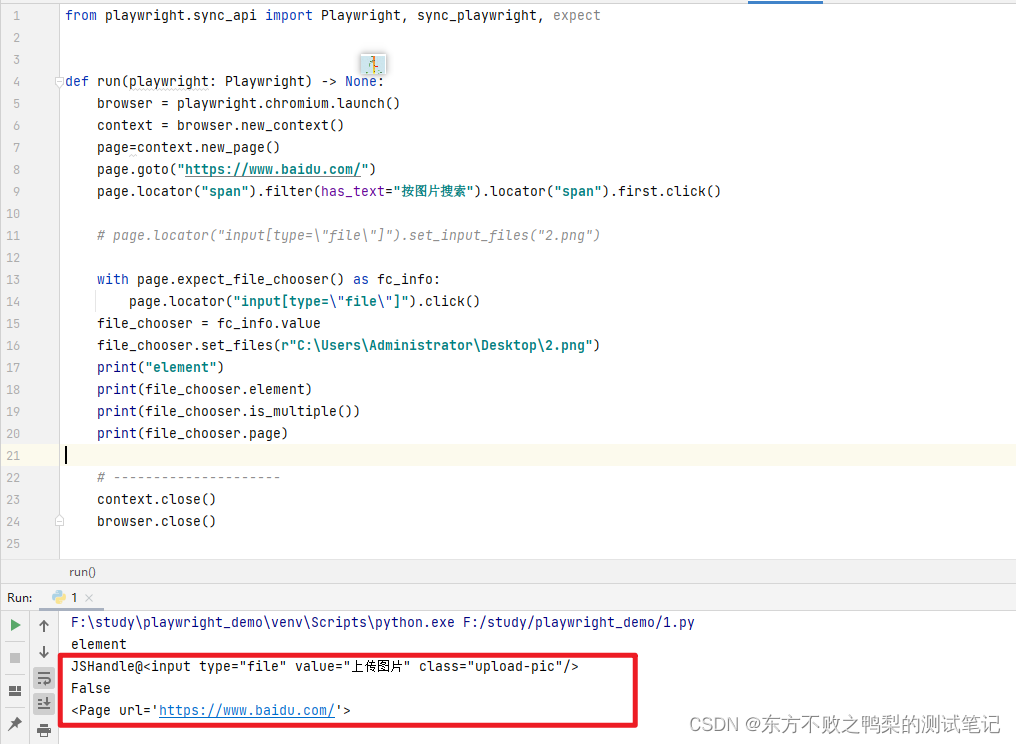
最强自动化测试框架Playwright(29)-文件选择对象
FileChooser对象通过page.on("filechoose")事件监听。 如下代码实现点击百度搜图按钮,上传文件进行搜索。 from playwright.sync_api import Playwright, sync_playwright, expectdef run(playwright: Playwright) -> None:browser playwright.chro…...

【烂尾】K8S部署
0x01 初见K8S 在地下城的迷宫深处,有一个神奇的存在,它就是Kubernetes!宛如一个勇敢的冒险者,它穿越着这个复杂的迷宫,带领着容器们战胜各种惊险的挑战。 Kubernetes就像是一位无所畏惧的剑士,手握着强大…...
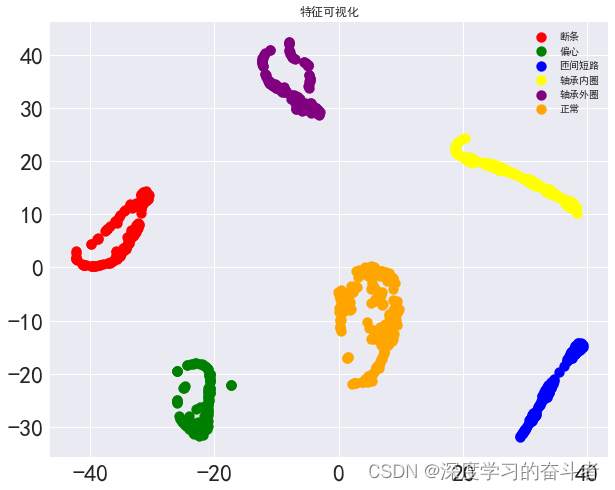
电机故障诊断(python程序,模型为MSCNN结合LSTM结合注意力机制模型,有注释)
代码运行环境要求:TensorFlow版本>2.4.0,python版本>3.6.0 1.电机常见的故障类型有以下几种: 轴承故障:轴承是电机运转时最容易受损的部件之一。常见故障包括磨损、疲劳、过热和润滑不良,这些问题可能导致噪音增…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
