西电_数字信号处理二_学习笔记
相关文章：
西电_数字信号处理二_学习笔记
文章目录【 第1章 离散随机信号 】【 第2章 维纳滤波 】【 第3章 卡尔曼滤波 】【 第4章 自适应滤波 】【 第5章 功率谱估计 】这是博主2022秋季所学数字信号处理二的思维导图（软件是幕布），供大家参考，如内容上有不妥之处…...
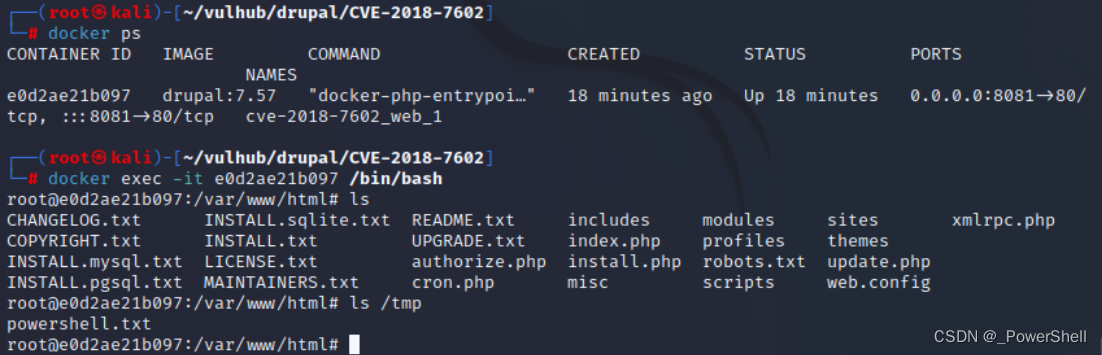
[ vulhub漏洞复现篇 ] Drupal 远程代码执行漏洞（CVE-2018-7602）
🍬 博主介绍 👨🎓 博主介绍：大家好，我是 _PowerShell ，很高兴认识大家~ ✨主攻领域：【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...
MySQL最佳实践
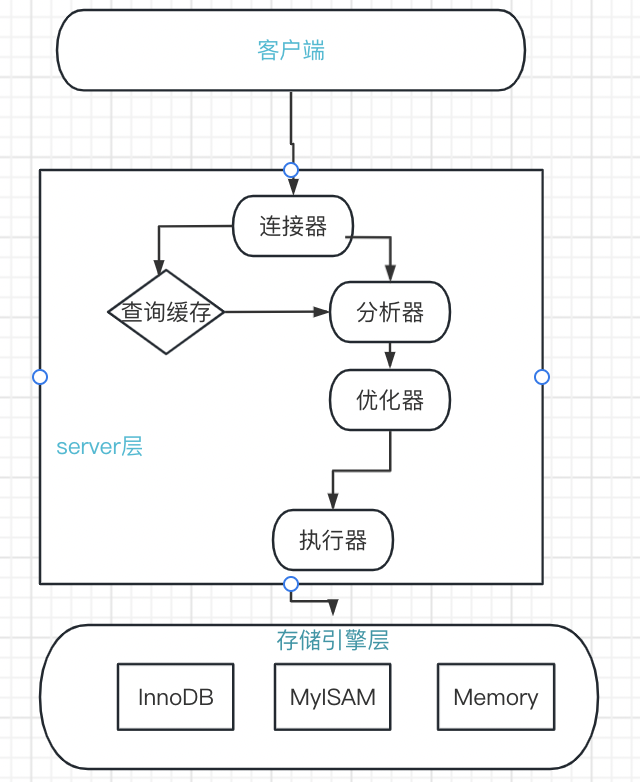
一、MySQL查询执行过程 1.MySQL分层结构 MySQL8.0没有查询缓存的功能了,如果频繁修改缓存,将会损耗性能查询流程就按照分层结构就可以清楚,只要了解各个组件的各自功能就行分析器主要分析语法和词法是否正确优化器主要优化SQL语句 二、MySQL更新执行过程 更新主要涉及两个重…...
Python 之 Matplotlib 散点图、箱线图和词云图
文章目录一、散点图1. scatter() 函数2. 设置图标大小3. 自定义点的颜色和透明度4. 可以选择不同的颜色条，配合 cmap 参数5. cmap 的分类5.1 Sequential colormaps：连续化色图5.2 Diverging colormaps：两端发散的色图 .5.3 Qualitative color…...
SpringCloud(三)Hystrix断路器服务降级、服务熔断、服务监控案例详解
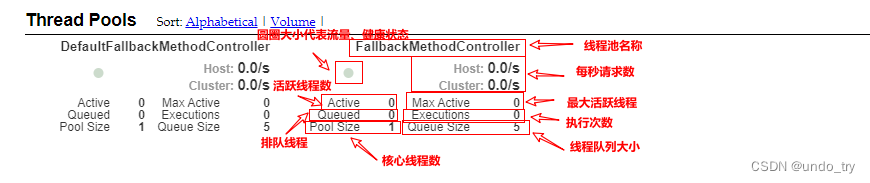
七、Hystrix断路器 7.1 简介 分布式系统面临的问题 复杂分布式体系结构中的应用程序有数十个依赖关系，每个依赖关系在某些时候将不可避免地失败。 多个微服务之间调用的时候，假设微服务A调用微服务B和微服务C，微服务B和微服务C又调用其它的微…...
【超好用】自定义的mybatis-plus代码生成器
BACKGROUND你是否也有这样的烦恼：每次写代码都需要创建很多包很多层很多类很多接口？耗时且费力姑且不谈，有时可能还大意了没有闪，搞出一堆bug这谁顶得住啊都3202年了，让程序自力更生吧！！教程 le…...
Kubernetes学习笔记-计算资源管理（4）监控pod的资源使用量20230219
前面学了设置资源的requests和limits，这节课学习如何监控资源，根据监控资源使用情况，对requests和limits进行合理配置。收集、获取实际资源使用情况kubelet包含一个agent，名为cAdvisor，它会收集整个节点上运行的所有单…...
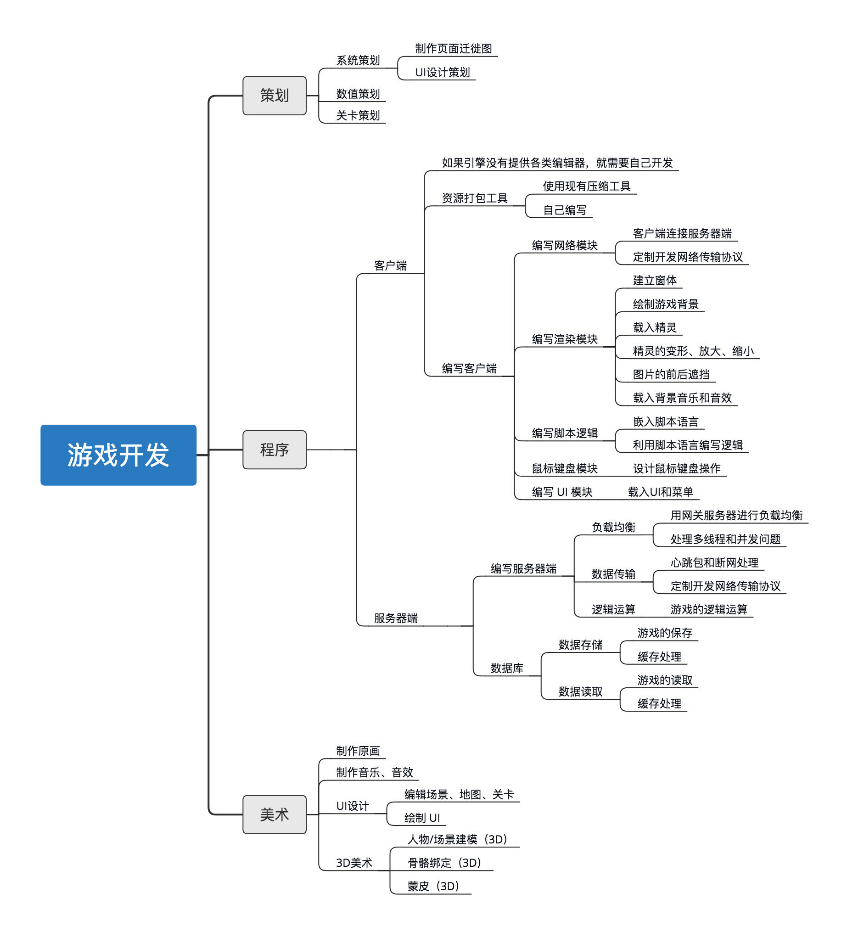
游戏开发 - 开发流程 - 收集
1.应用场景 主要用于了解，掌握游戏开发的整个流程。 2.学习/操作 1.文档阅读 复习课 | 带你梳理客户端开发的三个重点-极客时间 2.整理输出 2.1 游戏开发流程 -- 参考 按照游戏开发中的三大模块策划、程序、美术，画了一个图。 开发游戏的时候ÿ…...
LA@向量空间@坐标变换
文章目录向量空间向量空间的属性坐标例基变换坐标变换n维向量空间RnR^nRn子空间例线性组合与线性方程组生成子空间深度学习向量空间 设VVV是n维向量的非空集合,如果VVV对向量的加法和数乘运算封闭,即 ∀α,β∈V,∀k∈Rαβ,kα∈V\forall \alpha,\beta\in{V},\forall k\in{\ma…...
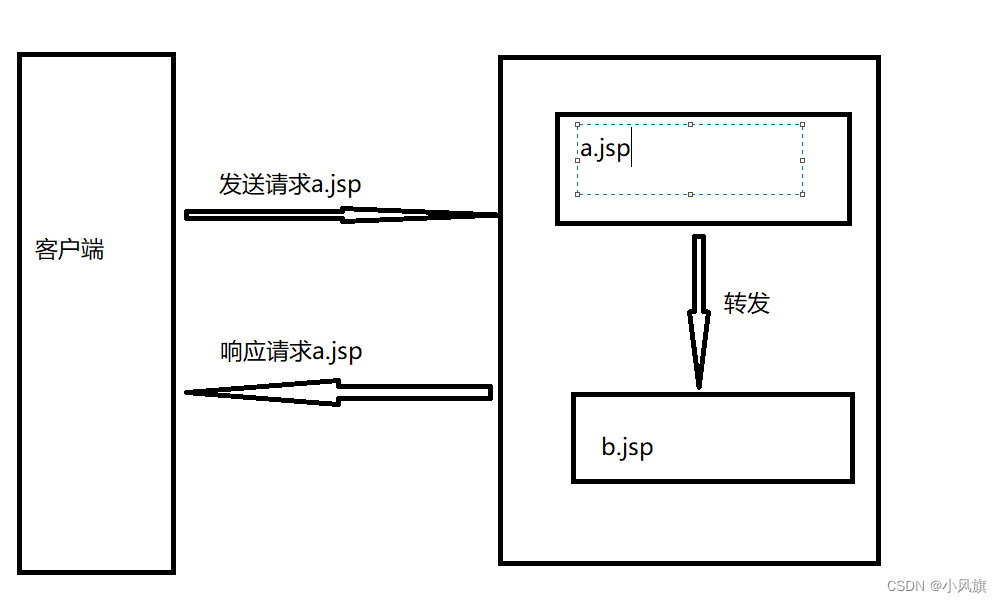
JSP脚本指令及标记学习笔记
好久没更新文章了，上次更新的文章还是一个学习笔记。本篇博文介绍的是JSP基本概念 1.JSP开发方法 一个jsp网页只需要加上<%%>就行了。 2.JSP运行机制 3.JSP脚本元素 3.1 JSP脚本代码 <% 脚本代码 %>实例 <% SimpleDateFormat df new SimpleDa…...
【C语言每日一题】——猜凶手
【C语言每日一题】——猜名次😎前言🙌猜凶手🙌解题思路分享：😍解题源码分享：😍总结撒花💞😎博客昵称：博客小梦 😊最喜欢的座右铭：全神…...
2019蓝桥杯真题完全二叉树的权值 C语言/C++
题目描述 给定一棵包含 N个节点的完全二叉树，树上每个节点都有一个权值，按从 上到下、从左到右的顺序依次是 A_1, A_2, A_N，如下图所示： 现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点 权值之和最…...
大数据之Phoenix环境搭建
文章目录前言一、下载Phoenix安装包二、上传并解压三、拷贝服务包到各个hbase的lib目录下四、修改hbase的配置文件五、重启HBase集群六、连接Phoenix客户端前言 #博学谷IT学习技术支持# 本篇文章主要介绍Phoenix的环境搭建，Phoenix支持使用SQL语句操作HBase&#x…...
62 一次 Promotion failed 的调试
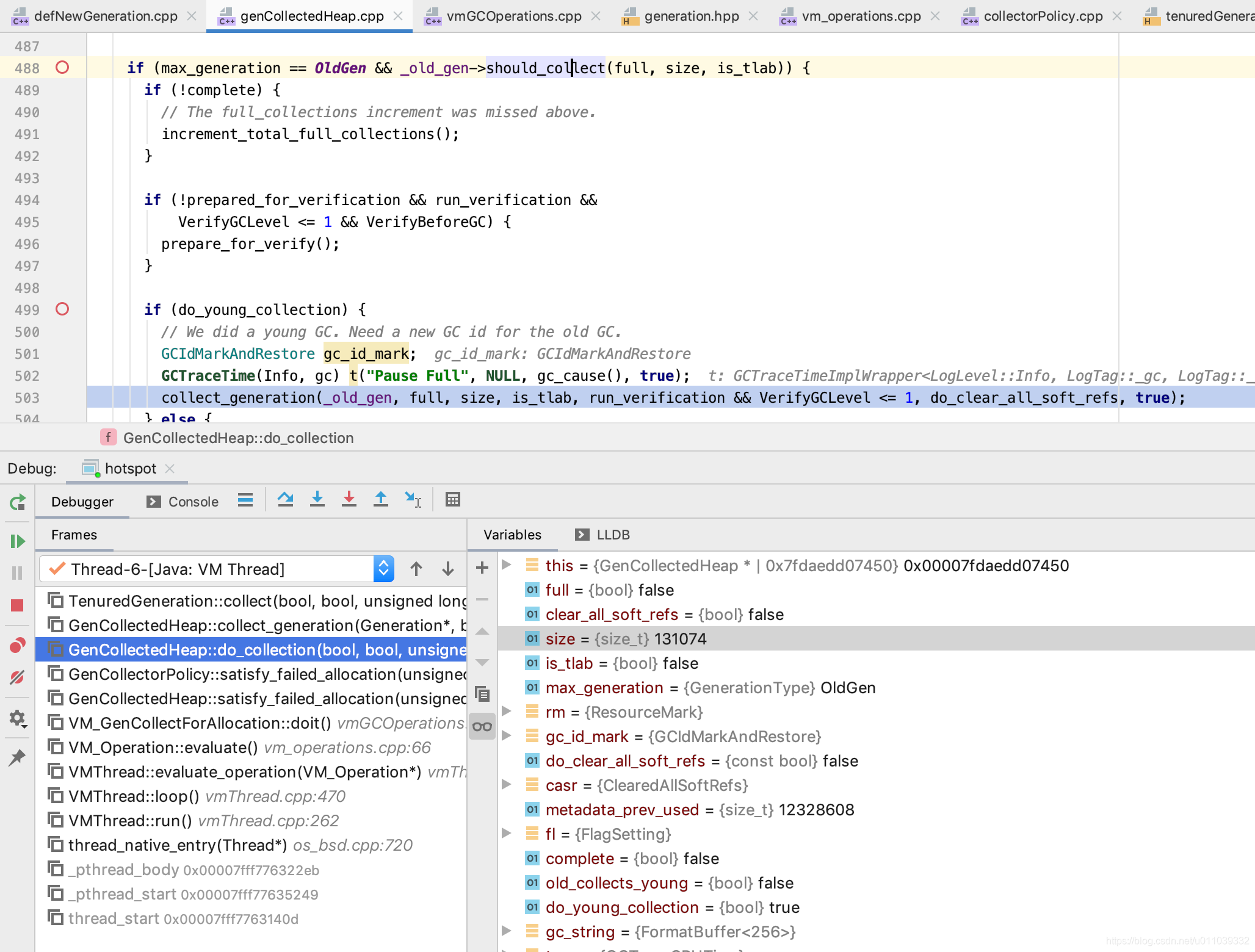
前言 最近 有一个想法就是, 调试一下 DefNewGeneration 里面的晋升失败的情况 呵呵 对于这块的代码上面, 看着感觉有一些疑问的地方, 因此想通过 实际的调试, 来验证一下 实际的情况 然后 之前写了一个用例, 但是 和心中的期望差距甚大, 当然 主要的问题 还是自己对于 细…...
Git的基本操作
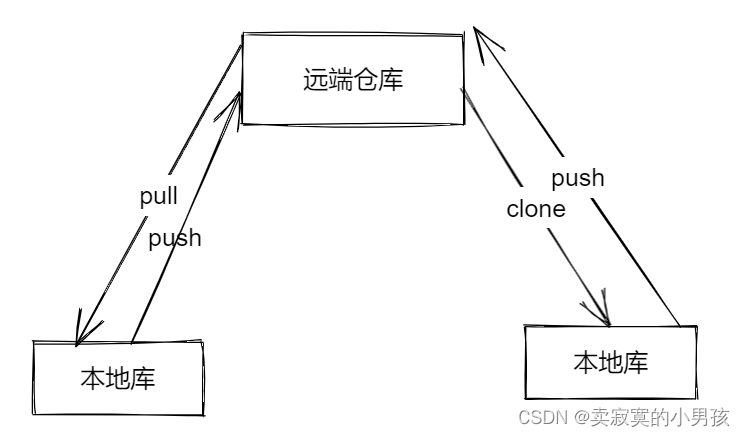
文章目录1.git的工作流程2.git的工作环境3.git的基本操作(1)git init(2)git status(3)git add(4)git commit4.版本控制(1)git reflog与git log(2)再增加两个版本(3)git reset --hard 版本号(4)两个指针4.分支管理(1)对分支的理解(2)git branch和git branch -v(3)git checkout 分…...
LeetCode初级算法题：两数之和+斐波拉契数列多种java解法
目录7 两数之和题目描述：解题思路与代码暴力解法：解法一：二分查找解法二：双指针2 斐波那契数列题目描述：解题思路与代码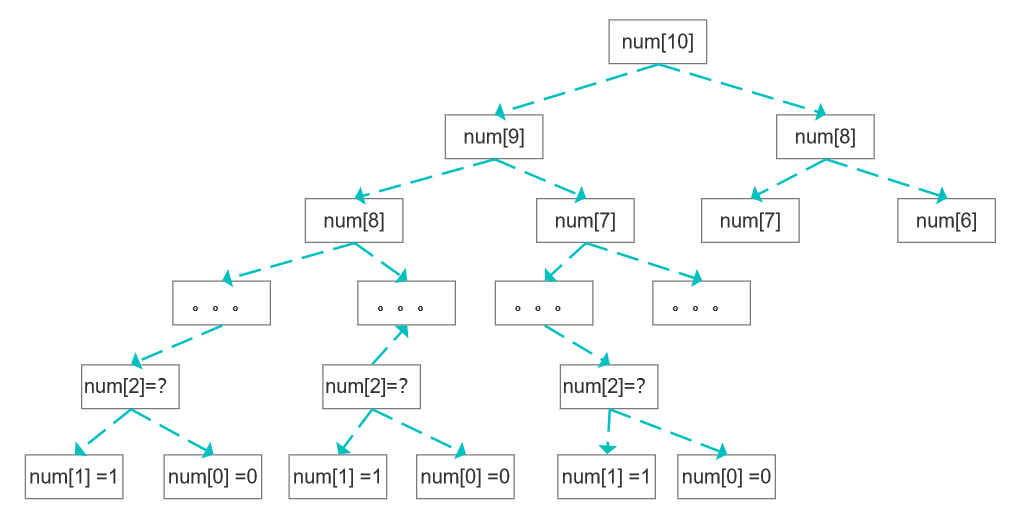解法一&…...
测试1：测试相关概念
1.测试相关概念 1.1.测试概念 1.1.1.需求 符合正式文档规定的条件和权能，包括用户需求和软件需求 它们之间的的转换是：沟通 用户需求和软件需求的区别： 能否指导开发人员开发，测试人员编写测试用例 1.1.2.缺陷Bug 与正确的…...
2.19 索引和事务
一.联合查询面试问题:聚合查询与联合查询的区别聚合查询是行与行之间的数据加工聚合函数 :count,sum,avg...group by 进行分组,指定列的值,相同的记录合并到同一个组,每个组又可以分别进行聚合查询分组还可以指定条件筛选,如果分组之前指定条件 用where,如果对分组之后指定条件…...
算法导论【摊还分析】—聚合分析、核算法、势能法
算法导论【摊还分析】—聚合分析、核算法、势能法聚合分析核算法势能法假定我们对一个数据结构执行一个由 n 个操作组成的操作序列，当 i 严格为 2 的幂时，第 i 个操作的代价为 i，否则代价为 1 聚合分析 总共有n个操作，1,2,4.....…...
【LeetCode】剑指 Offer 08. 二叉树的下一个节点 p65 -- Java Version
题目链接：无题目链接，不知道为啥力扣上找不到这一题。 1. 题目介绍（08. 二叉树的下一个节点） 题目：给定一个二叉树和其中的一个节点，请找出中序遍历顺序的下一个节点并且返回。注意，树中的节点…...
第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架，它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用，和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...
基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容：参考网站： PID算法控制 PID即：Proportional（比例）、Integral（积分&…...
【Java学习笔记】Arrays类
Arrays 类 1. 导入包：import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序（自然排序和定制排序）Arrays.binarySearch()通过二分搜索法进行查找（前提：数组是…...
【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台，覆盖应用全生命周期测试需求，主要提供五大核心能力： 测试类型检测目标关键指标功能体验基…...
java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具，自己手写的难度，恐怕高级程序员花费一年的事件，也…...
linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 （忘了有没有这步了 估计有） 刷机程序 和 镜像 就不提供了。要刷的时…...
MySQL账号权限管理指南：安全创建账户与精细授权技巧
在MySQL数据库管理中，合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号？ 最小权限原则…...
SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理）
上一章用到了V2 的概念，其实 Fiori当中还有 V4，咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务)，代理中间件（ui5-middleware-simpleproxy）-CSDN博客…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达，从日常对话到特定领域的文档（例如医学文档）（Heritage 2013；Landmark、Gulbrandsen 和 Svenevei…...
React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store： 我们在使用异步的时候理应是要使用中间件的，但是configureStore 已经自动集成了 redux-thunk，注意action里面要返回函数 import { configureS…...