【数据结构与算法——TypeScript】树结构Tree
【数据结构与算法——TypeScript】
树结构(Tree)
认识树结构以及特性
什么是树?
🌲 真实的树:相信每个人对现实生活中的树都会非常熟悉
🌲 我们来看一下树有什么特点?
▫️ 树通常有一个根。连接着根的是树干。
▫️ 树干到上面之后会进行分叉成树枝,树枝还会分叉成更小的树枝。
▫️ 在树枝的最后是叶子。
🌲 树的抽象:
🌳 专家们对树的结构进行了抽象,发现树可以模拟生活中的很多场景。
模拟树结构
-
公司组织架构

-
前端非常熟悉的DOM Tree


树结构的抽象
❤️🔥 我们再将里面的数据移除,仅仅抽象出来结构,那么就是我们要学习的树结构

树结构的优点和术语
树结构的优点
🖤 我们之前已经学习了多种数据结构来保存数据,为什么要使用树结构来保存数据呢?
🖤 树结构和数组/链表/哈希表的对比有什么优点呢?
💚 数组:
❤️ 优点:
- 数组的主要优点是根据下标值访问效率会很高。
- 但是如果我们希望根据元素来查找对应的位置呢?
- 比较好的方式是先对数组进行排序,再进行二分查找。
- 链表的插入和删除操作效率都很高。
💔 缺点:
- 需要先对数组进行排序,生成有序数组,才能提高查找效率。
- 另外数组在插入和删除数据时,需要有大量的位移操作(插入到首位或者中间位置的时候),效率很低。
💚 链表:
❤️ 优点:
- 链表的插入和删除操作效率都很高。
💔 缺点:
- 查找效率很低,需要从头开始依次访问链表中的每个数据项,直到找到。
- 而且即使插入和删除操作效率很高,但是如果要插入和删除中间位置的数据,还是需要重头先找到对应的数据。
💚 哈希表:
❤️ 优点:
- 我们学过哈希表后,已经发现了哈希表的插入/查询/删除效率都是非常高的。
- 但是哈希表也有很多缺点。。
💔 缺点:
- 空间利用率不高,底层使用的是数组,并且某些单元是没有被利用的。
- 哈希表中的元素是无序的,不能按照固定的顺序来遍历哈希表中的元素。
- 不能快速的找出哈希表中的最大值或者最小值这些特殊的值。
💚 树结构:
❤️ 优点:
- 我们不能说树结构比其他结构都要好,因为每种数据结构都有自己特定的应用场景。
- 但是树确实也综合了上面的数据结构的优点(当然优点不足于盖过其他数据结构,比如效率一般情况下没有哈希表高)。
- 并且也弥补了上面数据结构的缺点。。
💚 而且为了模拟某些场景,我们使用树结构会更加方便。
- 因为数结构的非线性的,可以表示一对多的关系
- 比如文件的目录结构。
树的术语
-
💚 在描述树的各个部分的时候有很多术语。
- 为了让介绍的内容更容易理解,需要知道一些树的术语。
- 不过大部分术语都与真实世界的树相关,或者和家庭关系相关(如父节点和子节点),所以它们比较容易理解。
-
❤️🔥 树(Tree):n(n≥0)个节点构成的有限集合。
- 当n=0时,称为空树;
-
对于任一棵非空树(n>0),它具备以下性质:
- 树中有一个称为“根(Root)”的特殊节点,用r表示;
- 其余节点可分为m(m>0)个互不相交的有限集T1,T2,Tm,其中每个集合本身又是一棵树,称为原来树的子树(SubTree)。

-
🌲 树的术语
- 节点的度(Degree):节点的子树个数。
- 树的度(Degree):树的所有节点中最大的度数。
- 叶节点(Leaf):度为0的节点。(也称为叶子节点)
- 父节点(Parent):有子树的节点是其子树的根节点的父节点
- 子节点(Child):若A节点是B节点的父节点,则称B节点是A节点的子节点;子节点也称孩子节点。
- 兄弟节点(Sibling):具有同一父节点的各节点彼此是兄弟节点。
- 路径和路径长度:从节点n1到nk的路径为一个节点序列n1,n2,nk
- ni是n(i+1)的父节点
- 路径所包含边的个数为路径的长度。
- 节点的层次(Level):规定根节点在1层,其它任一节点的层数是其父节点的层数加1。
- 树的深度(Depth):对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0。
- 树的高度(Height):对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0。

普通的表示方式
-
最普通的表示方式

-
儿子-兄弟表示法

- 儿子-兄弟表示法旋转

- 其实所有树本质上都可以用二叉树模拟出来
二叉树特性以及概念
二叉树的概念
- 如果树中每个节点最多只能有两个子节点,这样的树就成为 “二叉树”。
- 前面,我们已经提过二叉树的重要性,不仅仅是因为简单,也因为几乎上所有的树都可以表示成二叉树的形式。
- 💚 二叉树的定义
- 二叉树可以为空,也就是没有节点。
- 若不为空,则它是由根节点 和 称为其 左子树TL和 右子树TR 的两个不相交的二叉树组成。
- 二叉树有五种形态:

二叉树的特性
- 二叉树有几个比较重要的特性,在笔试题中比较常见:
- 一颗二叉树第 i 层的最大节点数为:2^(i-1),i >= 1;
- 深度为k的二叉树有最大节点总数为: 2^k - 1,k >= 1;
- 对任何非空二叉树T,若n0表示叶节点的个数、n2是度为2的非叶节点个数,那么两者满足关系 n0 = n2 + 1。

完美二叉树
- 完美二叉树(Perfect Binary Tree) ,也称为满二叉树(Full Binary Tree)
- 在二叉树中,除了最下一层的叶节点外,每层节点都有2个子节点,就构成了满二叉树。

完全二叉树
-
完全二叉树(Complete Binary Tree)
- 除二叉树最后一层外,其他各层的节点数都达到最大个数。
- 且最后一层从左向右的叶节点连续存在,只缺右侧若干节点。
- 完美二叉树是特殊的完全二叉树。

-
下面不是完全二叉树,因为D节点还没有右节点,但是E节点就有了左右节点。

二叉树常见存储方式
🟢 二叉树的存储常见的方式是数组和链表
使用数组
-
完全二叉树:按从上至下、从左到右存储

-
非完全二叉树:
- 非完全二叉树要转成完全二叉树才可以按照上面的方案存储
- 但,会造成很大的空间浪费

使用链表
- 二叉树最常见的方式还是使用链表存储
- 每个节点封装成一个Node,Node中包含存储的数据,左节点的引用,右节点的引用。


- 每个节点封装成一个Node,Node中包含存储的数据,左节点的引用,右节点的引用。
认识二叉搜索树特性
什么是二叉搜索树?
-
🟢 二叉搜索树(BST,Binary Search Tree),也称 二叉排序树或 二叉查找树。
-
二叉搜索树是一颗二叉树,可以为空
-
如果部位空,满足以下性质:
-
- 非空左子树的所有键值小于其根节点的键值
-
- 非空右子树的所有键值大于其根节点的键值
-
- 左、右子树本身也都是二叉搜索树
-
-
下面哪些是二叉搜索树,哪些不是?

-
💡 二叉搜索树的特点:
- ✅ 二叉搜索树的特点就是相对 较小的值总是保存在左节点上,相对较大的值总是保存在 右节点上
- ✅ 查找效率高,这也是二叉搜索树中,搜索的来源
二叉搜索树
-
下面是一个二叉搜索树

-
试着 查找一下值为10的节点

- ⭕️ 这种方式就是二分查找的思想:
- 查找所需的最大次数 等于 二叉搜索树的深度。
- 插入节点时,也 利用类似的方法,一层层比较大小,找到新节点合适的位置。
二叉搜索树类的封装
-
💡 先封装一个BSTree的类

-
👩🏻💻 代码解析
- 封装一个BSTree的类
- 还需要封装一个用于保存每一个节点的类 Node
- 该类包含三个属性:节点对应的value、指向的左子节点树left、指向的右子节点树right
- 对于BSTree来说,只需要保存根节点即可,因为其他节点都可以通过根节点找到
-
代码
import { Node } from '../types/INode';class IBSTreeNode<T> extends Node<T> {left: IBSTreeNode<T> | null = null;right: IBSTreeNode<T> | null = null;}class BSTree<T> {root: IBSTreeNode<T> | null = null;}export {};
export class Node<T> {value: T;constructor(value: T) {this.value = value;}}
二叉搜索树插入操作
- 二叉搜索树常见操作
1. 插入操作
🔶 insert (value):向树中插入一个新的数据。
2. 查找操作
🔶 search (value):在树中查找一个数据,如果节点存在,则返回true;如果不存在,则返回false 。
🔶 min:返回树中最小的值/数据。
🔶 max:返回树中最大的值/数据。
3. 遍历操作
🔶 inOrderTraverse :通过中序遍历方式遍历所有节点。
🔶 preOrderTraverse :通过先序遍历方式遍历所有节点。
🔶 postOrderTraverse :通过后序遍历方式遍历所有节点。
🔶 levelOrderTraverse :通过层序遍历方式遍历所有节点。
4. 删除操作(有一点点复杂)
🔶 remove (value):从树中移除某个数据。
向树中插入数据:分两部分
-
首先,外界调用的
insert方法- 👩🏻💻 代码解析:
- 首先,根据传入的
value,创建对应的Node。 - 其次,向树中插入数据需要分成两种情况:
- 第一次插入,直接修改根节点即可。
- 其他次插入,需要进行相关的比较决定插入的位置。
- 在代码中的
insertNode方法,我们还没有实现,也是我们接下来要完成的任务。
- 首先,根据传入的
- 👩🏻💻 代码解析:
-
其次,插入非根节点
- 👩🏻💻 代码解析:
- 插入其他节点时,我们需要判断该值到底是插入到左边还是插入到右边。
- 判断的依据来自于新节点的value 和原来节点的value值的比较。
- 如果新节点的newvalue 小于原节点的oldvalue ,那么就向左边插入。
- 如果新节点的newvalue 大于原节点的oldvalue ,那么就向右边插入。
- 代码的1序号位置,就是准备向左子树插入数据。但是它本身又分成两种情况
- 情况一(代码1.1位置):左子树上原来没有内容,那么直接插入即可。
- 情况二(代码1.2位置):左子树上已经有了内容,那么就一次向下继续查找新的走向,所以使用递归调用即可。
- 代码的2序号位置,和1序号位置几乎逻辑是相同的,只是是向右去查找。
- 情况一(代码2.1位置):左右树上原来没有内容,那么直接插入即可。
- 情况二(代码2.2位置):右子树上已经有了内容,那么就一次向下继续查找新的走向,所以使用递归调用即可。
- 👩🏻💻 代码解析:
-
代码:
// 插入private insertNode(node: BSTreeNode<T>, newNode: BSTreeNode<T>) {if (newNode.value < node.value) {// 在左子树节点插入 : 查找空白位置if (node.left === null) {node.left = newNode;} else {this.insertNode(node.left, newNode);}} else {// 在右子节点查找空白位置if (node.right === null) {node.right = newNode;} else {this.insertNode(node.right, newNode);}}}insert(value: T): boolean {// 1. 根据value创建TreeNode节点const newNode = new BSTreeNode(value);// 2. 判断是否有根节点if (!this.root) {//当前树为空this.root = newNode;} else {// 递归this.insertNode(this.root, newNode);}return false;}// 打印树结构import { btPrint } from 'hy-algokit';// 打印树结构print() {btPrint(this.root);}// 测试代码const bst = new BSTree<number>();bst.insert(11);bst.insert(7);bst.insert(15);bst.insert(5);bst.insert(3);bst.insert(9);bst.insert(8);bst.insert(10);bst.insert(13);bst.insert(12);bst.insert(14);bst.insert(20);bst.insert(18);bst.insert(25);bst.insert(6);bst.print();

遍历二叉搜索树
前面,我们向树中插入了很多的数据,为了能很多的看到测试结果。我们先来学习一下树的遍历。
- ❗️ 注意:这里我们学习的树的遍历,针对所有的二叉树都是适用的,不仅仅是二叉搜索树。
- ❤️🔥 树的遍历:
- 遍历一棵树是指访问树的每个节点(也可以对每个节点进行某些操作,我们这里就是简单的打印)
- 但是树和线性结构不太一样,线性结构我们通常按照从前到后的顺序遍历,但是树呢?
- 应该从树的顶端还是底端开始呢? 从左开始还是从右开始呢?
- 二叉树的遍历常见的有四种方式:
- 先序遍历
- 中序遍历
- 后序遍历
- 层序遍历
先序遍历 preOrderTraverse
- 遍历过程为:
- 优先访问根节点;
- 之后访问其左子树;
- 再访问其右子树。

private preOrderTraverseNode(node: BSTreeNode<T> | null) {if (node) {console.log(node.value);this.preOrderTraverseNode(node.left);this.preOrderTraverseNode(node.right);}}preOrderTraverse() {this.preOrderTraverseNode(this.root);}
中序遍历 inOrderTraverse
- 遍历过程为:
- 中序遍历其左子树;
- 访问根节点;
- 中序遍历其右子树。

private inOrderTraverseNode(node: BSTreeNode<T> | null) {if (node) {this.inOrderTraverseNode(node.left);console.log(node.value);this.inOrderTraverseNode(node.right);}}inOrderTraverse() {this.inOrderTraverseNode(this.root);}
后序遍历 postOrderTraverse
- 遍历过程为:
- 后序遍历其左子树;
- 后序遍历其右子树;
- 访问根节点。

private postOrderTraverseNode(node: BSTreeNode<T> | null) {if (node) {this.postOrderTraverseNode(node.left);this.postOrderTraverseNode(node.right);console.log(node.value);}}postOrderTraverse() {this.postOrderTraverseNode(this.root);}
层序遍历 levelOrderTraverse
- 遍历过程为:
- 层序遍历很好理解,就是从上向下逐层遍历。
- 层序遍历通常我们会借助于队列来完成;
✓ 也是队列的一个经典应用场景;

- 代码分析
- 使用队列 : 遍历整个队列
- 访问队列中的出队元素
- 将出队的节点的左子节点和右子节点分别加入队列
levelOrderTraverse() {// 1. 如果没有根节点,那么不需要遍历if (!this.root) return;// 2. 创建一个队列const queue: BSTreeNode<T>[] = [];// 队列中第一个节点是根节点queue.push(this.root);// 3. 遍历队列的长度while (queue.length) {// 弹出队列中当前元素const current = queue.shift()!;console.log(current.value);// 将当前元素的左子节点和右子节点添加到队列if (current.left) {queue.push(current.left);}if (current.right) {queue.push(current.right);}}}
获取最大值和最小值
getMaxValue(): T | null {let current = this.root;while (current && current.right) {current = current.right;}return current?.value ?? null;}
getMinValue(): T | null {let current = this.root;while (current && current.left) {current = current.left;}return current?.value ?? null;}
search搜索特定的值
-
二叉搜索树不仅仅获取最值效率非常高,搜索特定的值效率也非常高。
- ❗️注意:这里的实现返回boolean类型即可。
-
💻 代码解析:
- 这里我们还是使用了递归的方式。
- 递归必须有退出条件,我们这里是两种情况下退出。
- node === null,也就是后面不再有节点的时候。
- 找到对应的value,也就是node.value === value的时候。
- 在其他情况下,根据node.的value和传入的value进行比较来决定向左还是向右查找。
- 如果node.value > value,那么说明传入的值更小,需要向左查找。
- 如果node.value < value,那么说明传入的值更大,需要向右查找。
-
代码:
// 搜索特定值private searchNode(node: BSTreeNode<T> | null, value: T): boolean {// 如果node为空if (node === null) return false;// 判断node节点的value和valueif (node.value < value) {return this.searchNode(node.right, value);} else if (node.value > value) {return this.searchNode(node.left, value);} else {return true;}}search(value: T): boolean {return this.searchNode(this.root, value);}
二叉搜索树的删除
二叉搜索树的删除有些复杂,我们一点点完成。
-
删除节点要从查找要删的节点开始,找到节点后,需要考虑三种情况:
- 该节点是叶节点(没有字节点,比较简单)
- 该节点有一个子节点(也相对简单)
- 该节点有两个子节点.(情况比较复杂)
-
我们先从查找要删除的节点入手
- 先找到要删除的节点,如果没有找到,不需要删除
- 找到要删除节点
- 删除叶子节点
- 删除只有一个子节点的节点
- 删除有两个子节点的节点
-
👩🏻💻 代码分析:
- 搜索节点,节点是否存在
- 不存在,不需要任何操作
- 删除的节点是一个叶子结点
- 拿到当前叶子结点的父节点parent:判断是左子节点还是右子节点
- parent.left = null
- parent.right = null
- 删除的节点有一个子节点
- 删除的节点有两个子节点
- 搜索节点,节点是否存在
class BSTreeNode<T> extends Node<T> {...parent: BSTreeNode<T> | null = null;get isLeft(): boolean {return !!(this.parent && this.parent.left === this);}get isRight(): boolean {return !!(this.parent && this.parent.right === this);}
}
// 重构searchNodeprivate searchNode(value: T): BSTreeNode<T> | null {let current = this.root;let parent: BSTreeNode<T> | null = null;while (current) {// 如果找到current,直接返回if (current.value === value) return current;// 继续往下找parent = current;if (current.value < value) {current = current.right;} else {current = current.left;}// 如果current有值,那么current保存自己的父节点if (current) {current.parent = parent;}}return null;}
remove(value: T): boolean {// 1. 搜索:当前要删除的值const current = this.searchNode(value);// 1.1 节点不存在,不需要任何操作if (!current) return false;return true;}
情况一:没有子节点
-
情况一:没有子节点
- 这种情况相对比较简单,我们需要检测current的left以及right是否都为null.
- 都为null之后还要检测一个东西,就是是否current就是根,都为null,并且为跟根,那么相当于要清空二叉树(当然,只是清空了根,因为只有它).
- 否则就把父节点的left或者right字段设置为null即可.
-
如果只有一个单独的根,直接删除即可
-
如果是叶节点,那么处理方式如下:

remove(value: T): boolean {// 2.获取三个元素:当前节点、当前节点父节点、是属于左子节点/右子节点// console.log('当前节点:', current.value, '当前节点父节点:', current.parent?.value);// 2. 删除的节点是一个叶子结点if (current.left === null && current.right === null) {if (current === this.root) {// 如果只有一个单独的根,直接删除即可this.root = null;} else if (current.isLeft) {// 父节点的左子节点current.parent!.left = null;} else {current.parent!.right = null;}return true;}return true;}
情况二:有一个子节点
- 情况二:有一个子节点
- 要删除的current节点,只有2个连接(如果有两个子节点,就是三个连接了),一个连接父节点,一个连接唯一的子节点.
- 需要从这三者之间:爷爷 - 自己 - 儿子,将自己(current)剪短,让爷爷直接连接儿子即可.
- 这个过程要求改变父节点的left或者right,指向要删除节点的子节点.
- 当然,在这个过程中还要考虑是否current就是根.
- 分析:
- 如果是根的情况,比较简单.
- 如果不是根,并且只有一个子节点的情况.

remove(value: T): boolean {// 3. 有一个子节点// 3.1 只有左子节点else if (current.right === null) {if (current === this.root) {this.root = current.left;} else if (current.isLeft) {current.parent!.left = current.left;} else {current.parent!.right = current.left;}}// 3.2 只有右子节点else if (current.left === null) {if (current === this.root) {this.root = current.right;} else if (current.isLeft) {current.parent!.left = current.right;} else {current.parent!.right = current.right;}}return true;}
情况三:两个子节点
💡 看下面的集中情况你怎么处理?
- 情况一:删除9节点
- 处理方式相对简单,将8位置替换到9,或者将10位置替换到9
- 注意:这里我说的是替换也就是8位置替换到9时7指向8,而8还需要指向10。
- 画图分析

- 情况二:删除7节点
- 一种方式是将5拿到7的位置,3依然指向5,但是5有一个right需要指向9。依然是二义搜索树,没有问题
- 另一种方式是在右侧找一个,找谁?8
- 也就是将8替换到7的位置,8的left指向5,right 指向9依然是二叉搜索树,没有问题
- 画图
-
- 情况三:删除15节点,并且我希望也在右边找
- 你找到的是谁?其实我们观察一下你能找到18
- 18替换15的位置,20的left指向19。也是一个二叉搜索树,也没有问题
- 画图

寻找规律
如果我们要删除的节点有两个子节点,甚至子节点还有子节点,这种情况下我们需要从下面的子节点中找到一个节点,来替换当前的节点.
- 但是找到的这个节点有什么特征呢? ❤️🔥 应该是current节点下面所有节点中最接近current节点的.
- 要么比current节点小一点点,要么比current节点大一点点。
- 总结你最接近current,你就可以用来替换current的位置.
- ❤️🔥 这个节点怎么找呢?
- 比current小一点点的节点,一定是current左子树的最大值。
- 比current大一点点的节点,一定是current右子树的最小值。
- 前驱&后继
- 在二叉搜索树中,这两个特别的节点,有两个特别的名字。
- 比current小一点点的节点,称为current节点的前驱。
- 比current大一点点的节点,称为current节点的后继。
- 也就是为了能够删除有两个子节点的current,要么找到它的前驱,要么找到它的后继。
- 所以,接下来,我们先找到这样的节点(前驱或者后继都可以,我这里以找后继为例)
删除两个子节点代码
// 获取右子树private getSuccessor(delNode: BSTreeNode<T>): BSTreeNode<T> {// 获取右子树let current = delNode.right;let successor: BSTreeNode<T> | null = null;while (current) {successor = current;current = current.left;if (current) {current.parent = successor;}}// 如果拿到了后继节点// console.log('删除节点:', delNode.value, '后继节点:', successor?.value);if (successor !== delNode.right) {successor!.parent!.left = successor!.right;successor!.right = delNode.right;}//一定: 将删除节点的left,赋值给后继节点的leftsuccessor!.left = delNode.left;return successor!;}
remove(value: T): boolean {// 4. 有两个子节点else {const successor = this.getSuccessor(current);if (current === this.root) {this.root = successor;} else if (current.isLeft) {current.parent!.left = successor;} else {current.parent!.right = successor;}}return true;}
树的平衡性
- 为了能以较快的时间O(logN)来操作一棵树,我们需要保证树总是平衡的:
- 至少大部分是平衡的,那么时间复杂度也是接近O(logN)的
- 也就是说树中每个节点左边的子孙节点的个数,应该尽可能的等于右边的子孙节点的个数。
- 常见的平衡树有哪些呢?
- AVL树:
- AVL树是最早的一种平衡树。它有些办法保持树的平衡(每个节点多存储了一个额外的数据)
- 因为AVL树是平衡的,所以时间复杂度也是O(logN)。
- 但是,每次插入/删除操作相对于红黑树效率都不高,所以整体效率不如红黑树
- 红黑树:
- 红黑树也通过一些特性来保持树的平衡。
- 因为是平衡树,所以时间复杂度也是在O(logN)。
- 另外插入/删除等操作,红黑树的性能要优于AVL树,所以现在平衡树的应用基本都是红黑树。
- AVL树:
【数据结构与算法——TypeScript】 系列
1 、【数据结构与算法——TypeScript】数组、栈、队列、链表
2 、【数据结构与算法——TypeScript】算法的复杂度分析、 数组和链表的对比
3 、【数据结构与算法——TypeScript】哈希表
相关文章:

【数据结构与算法——TypeScript】树结构Tree
【数据结构与算法——TypeScript】 树结构(Tree) 认识树结构以及特性 什么是树? 🌲 真实的树:相信每个人对现实生活中的树都会非常熟悉 🌲 我们来看一下树有什么特点? ▫️ 树通常有一个根。连接着根的是树干。 ▫️ 树干到…...

多维时序 | MATLAB实现PSO-CNN-BiGRU多变量时间序列预测
多维时序 | MATLAB实现PSO-CNN-BiGRU多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-CNN-BiGRU多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.多维时序 | MATLAB实现PSO-CNN-BiGRU多变量时间序列预测; 2.运行环境为Matlab20…...
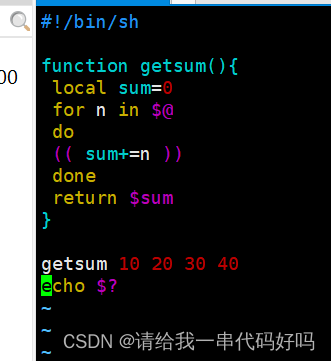
Shell 编程基础01
0:目录 1.创建新的虚拟机项目 2.linux常见命令和配置时间同步器 3.文件属性 4.if for while和方法 1.创建新的虚拟机项目 默认下一步到虚拟机命名 默认下一步设置磁盘大小 自定义硬件 删除打印机设置映像地址 启动虚拟机 选择 install centOS 7 选择英文 设置时…...
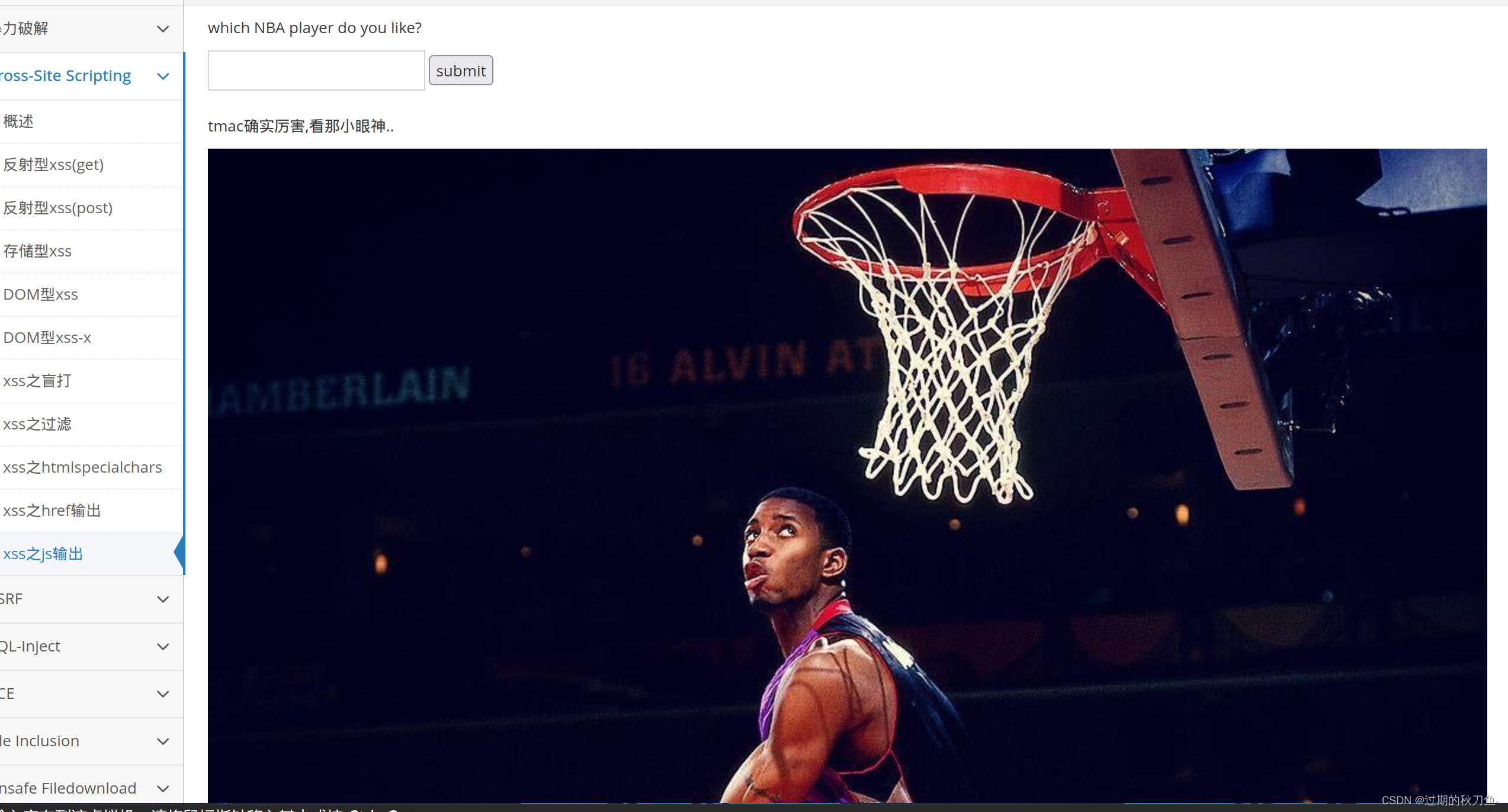
Cross-Site Scripting
文章目录 反射型xss(get)反射型xss(post)存储型xssDOM型xssDOM型xss-xxss-盲打xss-过滤xss之htmlspecialcharsxss之href输出xss之js输出 反射型xss(get) <script>alert("123")</script>修改maxlength的值 反射型xss(post) 账号admin密码123456直接登录 …...

基于java企业员工绩效考评系统设计与实现
摘 要 时代的变化速度实在超出人类的所料,21世纪,计算机已经发展到各行各业,各个地区,它的载体媒介-计算机,大众称之为的电脑,是一种特高速的科学仪器,比人类的脑袋要灵光无数倍,什么…...
SpringBoot 操作Redis、创建Redis文件夹、遍历Redis文件夹
文章目录 前言依赖连接 RedisRedis 配置文件Redis 工具类操作 Redis创建 Redis 文件夹查询数据遍历 Redis 文件夹 前言 Redis 是一种高性能的键值存储数据库,支持网络、可基于内存亦可持久化的日志型,而 Spring Boot 是一个简化了开发过程的 Java 框架。…...
c++11 标准模板(STL)(std::basic_stringbuf)(六)
定义于头文件 <sstream> template< class CharT, class Traits std::char_traits<CharT>, class Allocator std::allocator<CharT> > class basic_stringbuf : public std::basic_streambuf<CharT, Traits> std::basic_stringbu…...

iceberg系列之 hadoop catalog 小文件合并实战
背景 flink1.15 hadoop3.0pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://mave…...

神经网络基础-神经网络补充概念-25-深层神经网络
简介 深层神经网络(Deep Neural Network,DNN)是一种具有多个隐藏层的神经网络,它可以用来解决复杂的模式识别和特征学习任务。深层神经网络在近年来的机器学习和人工智能领域中取得了重大突破,如图像识别、自然语言处…...
MySQL— 基础语法大全及操作演示!!!(上)
MySQL—— 基础语法大全及操作演示(上) 一、MySQL概述1.1 、数据库相关概念1.1.1 MySQL启动和停止 1.2 、MySQL 客户端连接1.3 、数据模型 二、SQL2.1、SQL通用语法2.2、SQL分类2.3、DDL2.3.1 DDL — 数据库操作2.3.1 DDL — 表操作 2.4、DML2.4.1 DML—…...
[golang gin框架] 46.Gin商城项目-微服务实战之后台Rbac客户端调用微服务权限验证以及Rbac微服务数据库抽离
一. 根据用户的权限动态显示左侧菜单微服务 1.引入 后台Rbac客户端调用微服务权限验证功能主要是: 登录后显示用户名称、根据用户的权限动态显示左侧菜单,判断当前登录用户的权限 、没有权限访问则拒绝,参考[golang gin框架] 14.Gin 商城项目-RBAC管理,该微服务功能和上一节[g…...

域名和ip的关系
域名和ip的关系 一:什么是域名 域名,简称域名、网域,是由一串用点分隔的名字组成的上某一台计算机或计算机组的名称,用于在数据传输时标识 计算机的电子方位(有时也指地理位置)。网域名称系统,有时也简称为域名…...

excel日期函数篇1
1、DAY(serial_number):返回序列数表示的某月的天数 在括号内给出一个时间对象或引用一个时间对象(年月日),返回多少日 下面结果都为20 2、MONTH(serial_number):返回序列数表示的某年的月份 在括号内给出一个时间对…...

Leetcode151 翻转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 注意:输入字符串 s中可能会存在前导空格、尾随空格…...

PHP FTP的相关函数及简单使用示例
简介 FTP是ARPANet的标准文件传输协议,该网络就是现今Internet的前身。 PHP FTP函数是通过文件传输协议提供对文件服务器的客户端访问,FTP函数用于打开、登陆以及关闭连接,也用于上传、下载、重命名、删除以及获取服务器上文件信息。 安装 …...
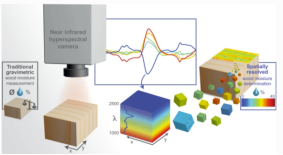
高光谱 | 矿物识别和分类标签数据制作、农作物病虫害数据分类、土壤有机质含量回归与制图、木材含水量评估和制图
本课程提供一套基于Python编程工具的高光谱数据处理方法和应用案例。 本课程涵盖高光谱遥感的基础、方法和实践。基础篇以学员为中心,用通俗易懂的语言解释高光谱的基本概念和理论,旨在帮助学员深入理解科学原理。方法篇结合Python编程工具,…...

【数据结构】二叉树篇| 纲领思路01+刷题
博主简介:努力学习的22级计算机科学与技术本科生一枚🌸博主主页: 是瑶瑶子啦每日一言🌼: 所谓自由,不是随心所欲,而是自我主宰。——康德 目录 一、二叉树刷题纲领二、刷题1、104. 二叉树的最大深度2、 二叉…...

系统架构设计师---计算机基础知识之数据库系统结构与规范化
目录 一、基本概念 二、 数据库的结构 三、常用的数据模型 概念数据模型...
PyCharm连接Docker中的容器(ubuntu)
一、为什么要用Pycharm链接Docker中的ubuntu 因为在进行深度学习的时候,基于windows系统在开发的过程中,老是出现很多问题,大多数是环境问题。 尽管安装了Conda,也不能很好的解决问题,使用ubuntu是最好的选择。 二、…...
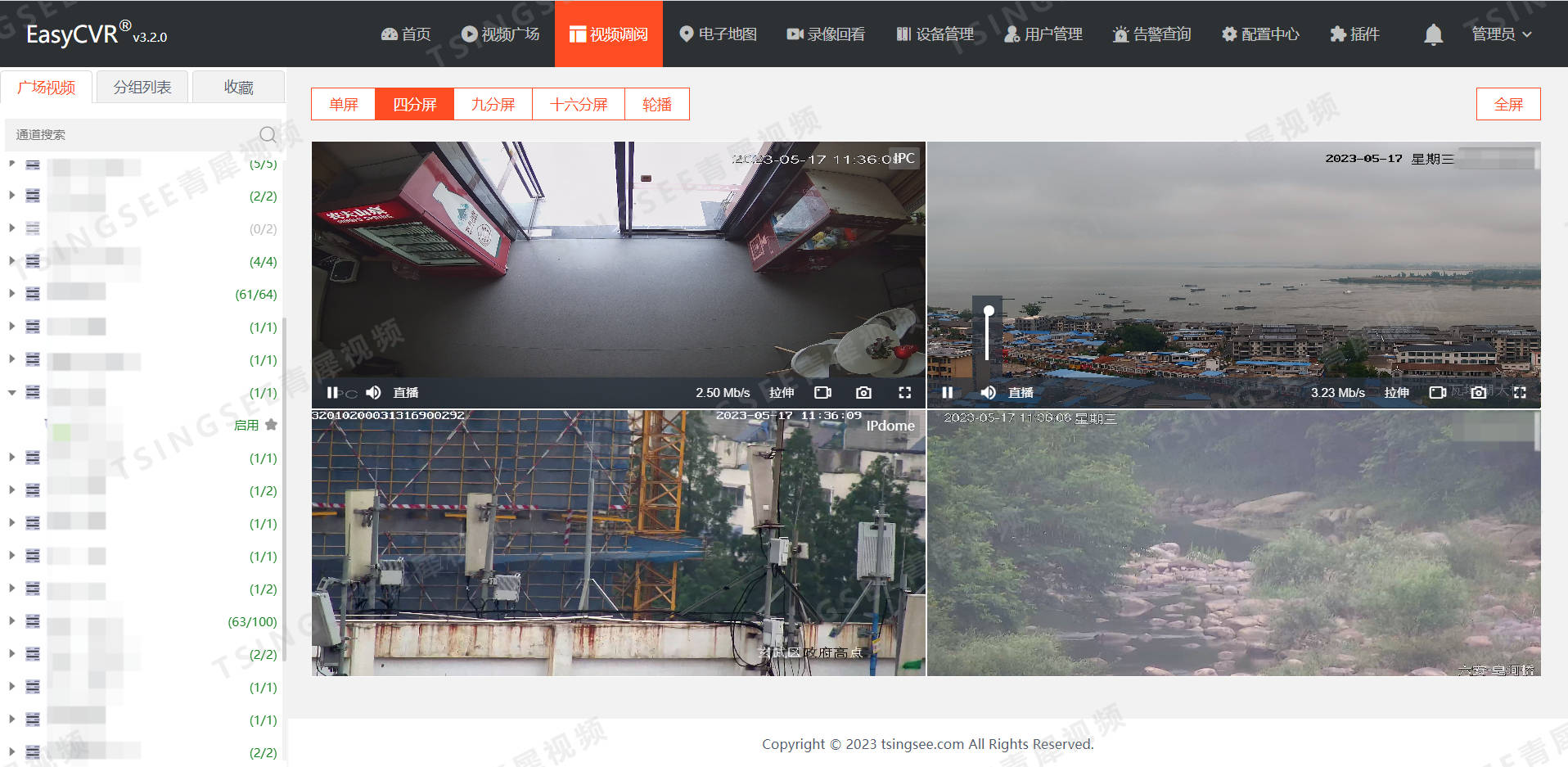
安防视频汇聚平台EasyCVR视频监控综合管理平台H.265转码功能更新,新增分辨率配置的具体步骤
安防视频集中存储EasyCVR视频监控综合管理平台可以根据不同的场景需求,让平台在内网、专网、VPN、广域网、互联网等各种环境下进行音视频的采集、接入与多端分发。在视频能力上,视频云存储平台EasyCVR可实现视频实时直播、云端录像、视频云存储、视频存储…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
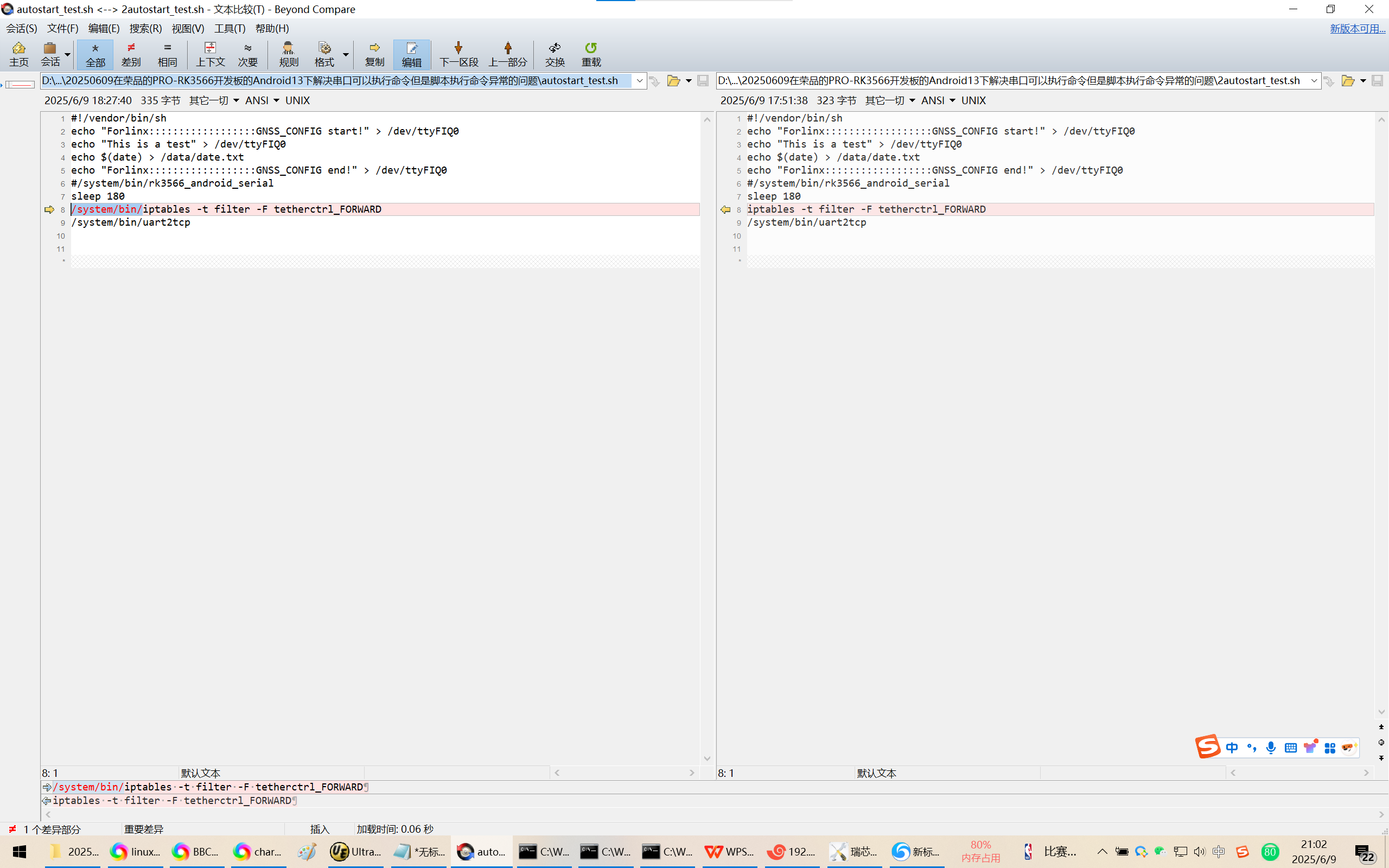
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...
