算法与数据结构(二十四)最优子结构原理和 dp 数组遍历方向
注:此文只在个人总结 labuladong 动态规划框架,仅限于学习交流,版权归原作者所有;
本文是两年前发的 动态规划答疑篇open in new window 的修订版,根据我的不断学习总结以及读者的评论反馈,我给扩展了更多内容,力求使本文成为继 动态规划核心套路框架 之后的一篇全面答疑文章。以下是正文。
这篇文章就给你讲明白以下几个问题:
1、到底什么才叫「最优子结构」,和动态规划什么关系。
2、如何判断一个问题是动态规划问题,即如何看出是否存在重叠子问题。
3、为什么经常看到将 dp 数组的大小设置为 n + 1 而不是 n。
4、为什么动态规划遍历 dp 数组的方式五花八门,有的正着遍历,有的倒着遍历,有的斜着遍历。
注:
可以通过子问题推导出原问题就是证明有最优子结构,而最优子结构 + 重叠子问题 = 动态规划;
一、最优子结构详解
「最优子结构」是某些问题的一种特定性质,并不是动态规划问题专有的。也就是说,很多问题其实都具有最优子结构,只是其中大部分不具有重叠子问题,所以我们不把它们归为动态规划系列问题而已。
我先举个很容易理解的例子:假设你们学校有 10 个班,你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩,你会不会算?当然会,而且你不用重新遍历全校学生的分数进行比较,而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。
我给你提出的这个问题就符合最优子结构:可以从子问题的最优结果推出更大规模问题的最优结果。让你算每个班的最优成绩就是子问题,你知道所有子问题的答案后,就可以借此推出全校学生的最优成绩这个规模更大的问题的答案。
你看,这么简单的问题都有最优子结构性质,只是因为显然没有重叠子问题,所以我们简单地求最值肯定用不出动态规划。
再举个例子:假设你们学校有 10 个班,你已知每个班的最大分数差(最高分和最低分的差值)。那么现在我让你计算全校学生中的最大分数差,你会不会算?可以想办法算,但是肯定不能通过已知的这 10 个班的最大分数差推到出来。因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差,比如全校的最大分数差可能是 3 班的最高分和 6 班的最低分之差。
这次我给你提出的问题就不符合最优子结构,因为你没办通过每个班的最优值推出全校的最优值,没办法通过子问题的最优值推出规模更大的问题的最优值。前文 动态规划详解 说过,想满足最优子结,子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间,显然子问题不独立,所以这个问题本身不符合最优子结构。
那么遇到这种最优子结构失效情况,怎么办?策略是:改造问题。对于最大分数差这个问题,我们不是没办法利用已知的每个班的分数差吗,那我只能这样写一段暴力代码:
int result = 0;
for (Student a : school) {for (Student b : school) {if (a is b) continue;result = max(result, |a.score - b.score|);}
}
return result;
改造问题,也就是把问题等价转化:最大分数差,不就等价于最高分数和最低分数的差么,那不就是要求最高和最低分数么,不就是我们讨论的第一个问题么,不就具有最优子结构了么?那现在改变思路,借助最优子结构解决最值问题,再回过头解决最大分数差问题,是不是就高效多了?
当然,上面这个例子太简单了,不过请读者回顾一下,我们做动态规划问题,是不是一直在求各种最值,本质跟我们举的例子没啥区别,无非需要处理一下重叠子问题。
前文不 同定义不同解法 和 高楼扔鸡蛋问题 就展示了如何改造问题,不同的最优子结构,可能导致不同的解法和效率。
再举个常见但也十分简单的例子,求一棵二叉树的最大值,不难吧(简单起见,假设节点中的值都是非负数):
int maxVal(TreeNode root) {if (root == null)return -1;int left = maxVal(root.left);int right = maxVal(root.right);return max(root.val, left, right);
}
你看这个问题也符合最优子结构,以 root 为根的树的最大值,可以通过两边子树(子问题)的最大值推导出来,结合刚才学校和班级的例子,很容易理解吧。
当然这也不是动态规划问题,旨在说明,最优子结构并不是动态规划独有的一种性质,能求最值的问题大部分都具有这个性质;但反过来,最优子结构性质作为动态规划问题的必要条件,一定是让你求最值的,以后碰到那种恶心人的最值题,思路往动态规划想就对了,这就是套路。
动态规划不就是从最简单的 base case 往后推导吗,可以想象成一个链式反应,以小博大。但只有符合最优子结构的问题,才有发生这种链式反应的性质。
找最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。这也是套路,经常刷题的读者应该能体会。
这里就不举那些正宗动态规划的例子了,读者可以翻翻历史文章,看看状态转移是如何遵循最优子结构的,这个话题就聊到这,下面再来看其他的动态规划迷惑行为。
注:
- 最优子结构只是动态规划问题的必要条件,比如求二叉树最大值,但是能求最值问题的大都具有最优子结构;
- 动态规划问题一定是让求最值的;
- 找最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。这也是套路,经常刷题的读者应该能体会;
二、如何一眼看出重叠子问题
经常有读者说:
看了前文 动态规划核心套路,我知道了如何一步步优化动态规划问题;
看了前文 动态规划设计:数学归纳法,我知道了利用数学归纳法写出暴力解(状态转移方程)。
但就算我写出了暴力解,我很难判断这个解法是否存在重叠子问题,从而无法确定是否可以运用备忘录等方法去优化算法效率。
对于这个问题,其实我在动态规划系列的文章中写过几次,在这里再统一总结一下吧。
首先,最简单粗暴的方式就是画图,把递归树画出来,看看有没有重复的节点。
比如最简单的例子,动态规划核心套路 中斐波那契数列的递归树:
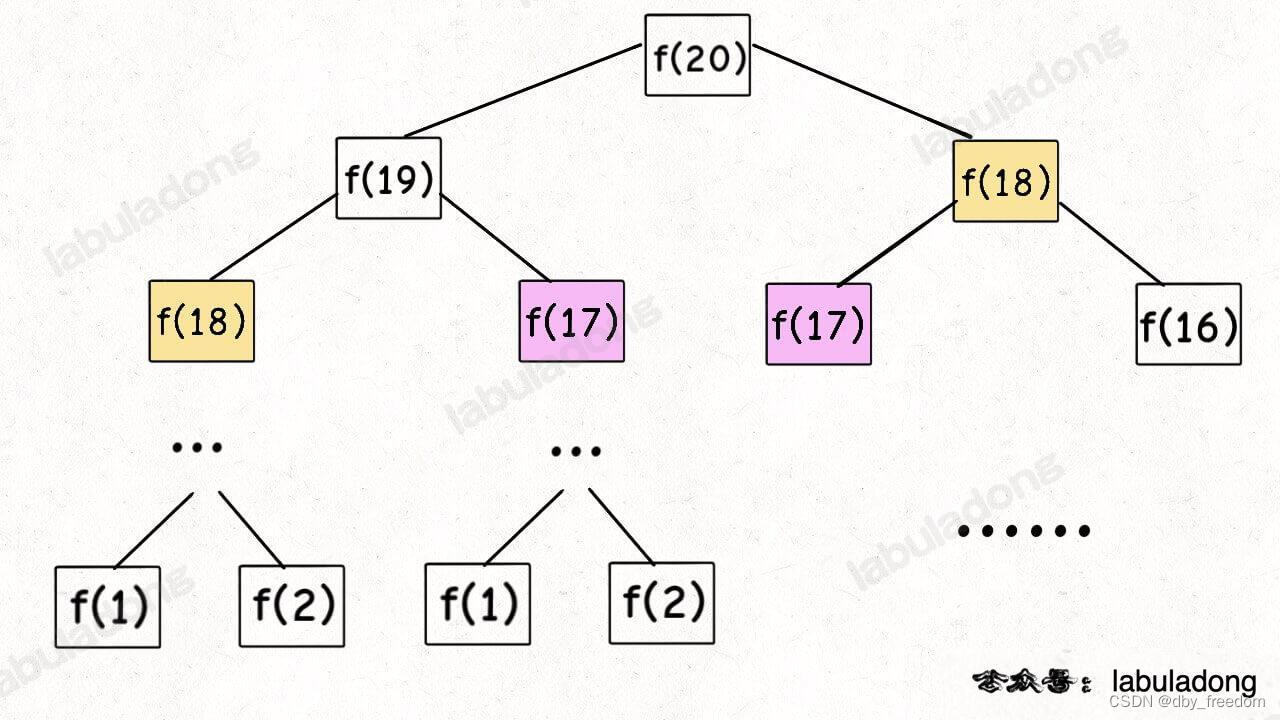
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
但毕竟斐波那契数列问题太简单了,实际的动态规划问题比较复杂,比如二维甚至三维的动态规划,当然也可以画递归树,但不免有些复杂。
比如在 最小路径和问题 中,我们写出了这样一个暴力解法:
int dp(int[][] grid, int i, int j) {if (i == 0 && j == 0) {return grid[0][0];}if (i < 0 || j < 0) {return Integer.MAX_VALUE;}return Math.min(dp(grid, i - 1, j), dp(grid, i, j - 1)) + grid[i][j];
}
你不需要读过前文,光看这个函数代码就能看出来,该函数递归过程中参数 i, j 在不断变化,即「状态」是 (i, j) 的值,你是否可以判断这个解法是否存在重叠子问题呢?
假设输入的 i = 8, j = 7,二维状态的递归树如下图,显然出现了重叠子问题:
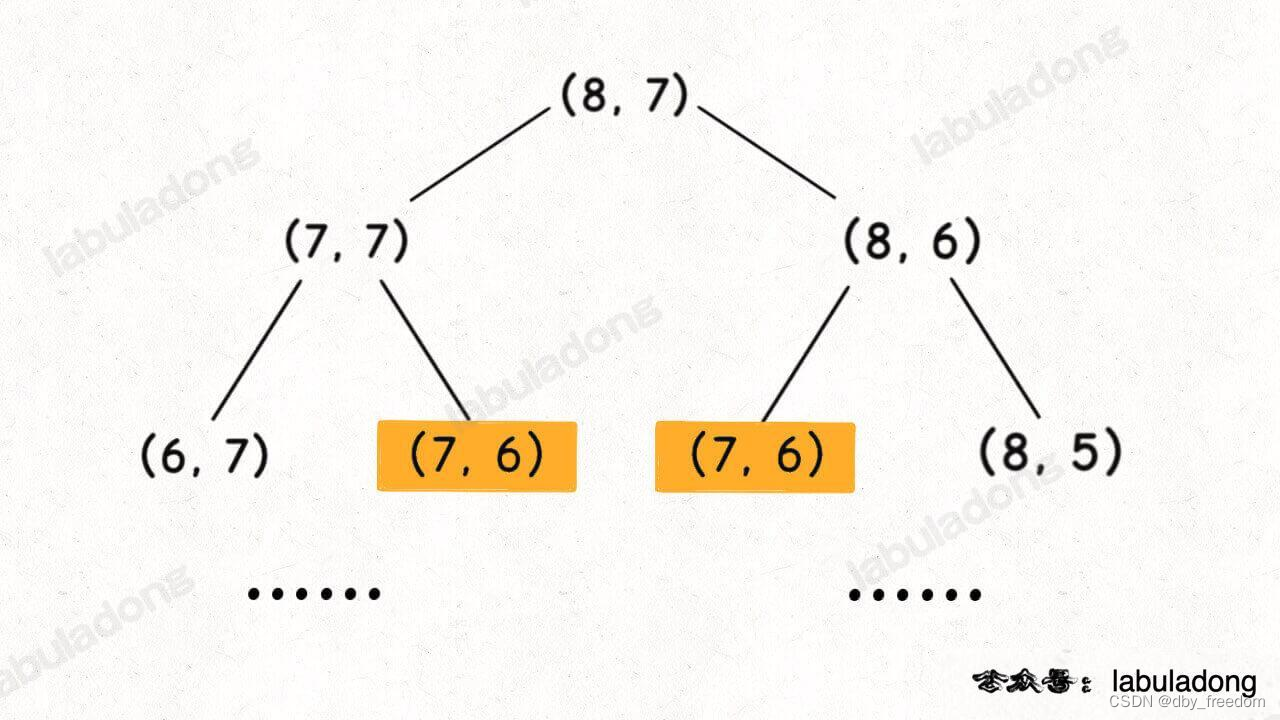
但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题。
具体操作就是直接删掉代码细节,抽象出该解法的递归框架:
int dp(int[][] grid, int i, int j) {dp(grid, i - 1, j), // #1dp(grid, i, j - 1) // #2
}
可以看到 i, j 的值在不断减小,那么我问你一个问题:如果我想从状态 (i, j) 转移到 (i-1, j-1),有几种路径?
显然有两种路径,可以是 (i, j) -> #1 -> #2 或者 (i, j) -> #2 -> #1,不止一种,说明 (i-1, j-1) 会被多次计算,所以一定存在重叠子问题。
再举个稍微复杂的例子,后文 正则表达式问题 的暴力解代码:
bool dp(string& s, int i, string& p, int j) {int m = s.size(), n = p.size();if (j == n) return i == m;if (i == m) {if ((n - j) % 2 == 1) return false;for (; j + 1 < n; j += 2) {if (p[j + 1] != '*') return false;}return true;}if (s[i] == p[j] || p[j] == '.') {if (j < n - 1 && p[j + 1] == '*') {return dp(s, i, p, j + 2)|| dp(s, i + 1, p, j);} else {return dp(s, i + 1, p, j + 1);}} else if (j < n - 1 && p[j + 1] == '*') {return dp(s, i, p, j + 2);}return false;
}
代码有些复杂对吧,如果画图的话有些麻烦,但我们不画图,直接忽略所有细节代码和条件分支,只抽象出递归框架:
bool dp(string& s, int i, string& p, int j) {dp(s, i, p, j + 2); // #1dp(s, i + 1, p, j); // #2dp(s, i + 1, p, j + 1); // #3
}
和上一题一样,这个解法的「状态」也是 (i, j) 的值,那么我继续问你问题:如果我想从状态 (i, j) 转移到 (i+2, j+2),有几种路径?
显然,至少有两条路径:(i, j) -> #1 -> #2 -> #2 和 (i, j) -> #3 -> #3,这就说明这个解法存在巨量重叠子问题。
所以,不用画图就知道这个解法也存在重叠子问题,需要用备忘录技巧去优化。
注:重叠子问题:最笨的方法是脑补一个递归树,看有没有重叠子问题;进一步可以通过递归框架判断是否有子问题,有子问题就可以考虑使用备忘录技巧去优化;
三、dp 数组的大小设置
比如说后文 编辑距离问题,我首先讲的是自顶向下的递归解法,实现了这样一个 dp 函数:
int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// 按照 dp 函数的定义,计算 s1 和 s2 的最小编辑距离return dp(s1, m - 1, s2, n - 1);
}// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp(s1, i, s2, j)
int dp(String s1, int i, String s2, int j) {// 处理 base caseif (i == -1) {return j + 1;}if (j == -1) {return i + 1;}// 进行状态转移if (s1.charAt(i) == s2.charAt(j)) {return dp(s1, i - 1, s2, j - 1);} else {return min(dp(s1, i, s2, j - 1) + 1,dp(s1, i - 1, s2, j) + 1,dp(s1, i - 1, s2, j - 1) + 1);}
}
然后改造成了自底向上的迭代解法:
int minDistance(String s1, String s2) {int m = s1.length(), n = s2.length();// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]int[][] dp = new int[m + 1][n + 1];// 初始化 base case for (int i = 1; i <= m; i++)dp[i][0] = i;for (int j = 1; j <= n; j++)dp[0][j] = j;// 自底向上求解for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 进行状态转移if (s1.charAt(i-1) == s2.charAt(j-1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1,dp[i][j - 1] + 1,dp[i - 1][j - 1] + 1);}}}// 按照 dp 数组的定义,存储 s1 和 s2 的最小编辑距离return dp[m][n];
}
这两种解法思路是完全相同的,但就有读者提问,为什么迭代解法中的 dp 数组初始化大小要设置为 int[m+1][n+1]?为什么 s1[0..i] 和 s2[0..j] 的最小编辑距离要存储在 dp[i+1][j+1] 中,有一位索引偏移?
能不能模仿 dp 函数的定义,把 dp 数组初始化为 int[m][n],然后让 s1[0..i] 和 s2[0..j] 的最小编辑距离要存储在 dp[i][j] 中?
理论上,你怎么定义都可以,只要根据定义处理好 base case 就可以。
你看 dp 函数的定义,dp(s1, i, s2, j) 计算 s1[0..i] 和 s2[0..j] 的编辑距离,那么 i, j 等于 -1 时代表空串的 base case,所以函数开头处理了这两种特殊情况。
再看 dp 数组,你当然也可以定义 dp[i][j] 存储 s1[0..i] 和 s2[0..j] 的编辑距离,但问题是 base case 怎么搞?索引怎么能是 -1 呢?
所以我们把 dp 数组初始化为 int[m+1][n+1],让索引整体偏移一位,把索引 0 留出来作为 base case 表示空串,然后定义 dp[i+1][j+1] 存储 s1[0..i] 和 s2[0..j] 的编辑距离。
注:dp 数组大小到底如何定义,依据 base case 来定,比如编辑距离问题中,base case dp[0][0] 代表空串情况,因此 dp 数组需要设置为 dp[m+1][n+1],把索引 0 留出来表示 base case 空串,做题时候,可以考虑下空串之类的情况再考虑设置 dp 数组大小;
四、dp 数组的遍历方向
我相信读者做动态规问题时,肯定会对 dp 数组的遍历顺序有些头疼。我们拿二维 dp 数组来举例,有时候我们是正向遍历:
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)// 计算 dp[i][j]
有时候我们反向遍历:
for (int i = m - 1; i >= 0; i--)for (int j = n - 1; j >= 0; j--)// 计算 dp[i][j]
有时候可能会斜向遍历:
// 斜着遍历数组
for (int l = 2; l <= n; l++) {for (int i = 0; i <= n - l; i++) {int j = l + i - 1;// 计算 dp[i][j]}
}
甚至更让人迷惑的是,有时候发现正向反向遍历都可以得到正确答案,比如我们在 团灭股票问题 中有的地方就正反皆可。
如果仔细观察的话可以发现其中的原因,你只要把住两点就行了:
1、遍历的过程中,所需的状态必须是已经计算出来的。
2、遍历结束后,存储结果的那个位置必须已经被计算出来。
注:
遍历开始时候,所需状态必须已经计算出来;
遍历结束时候,存储结果的位置必须已经计算出来;
下面来具体解释上面两个原则是什么意思。
比如编辑距离这个经典的问题,详解见后文 编辑距离详解,我们通过对 dp 数组的定义,确定了 base case 是 dp[..][0] 和 dp[0][..],最终答案是 dp[m][n];而且我们通过状态转移方程知道 dp[i][j] 需要从 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 转移而来,如下图:
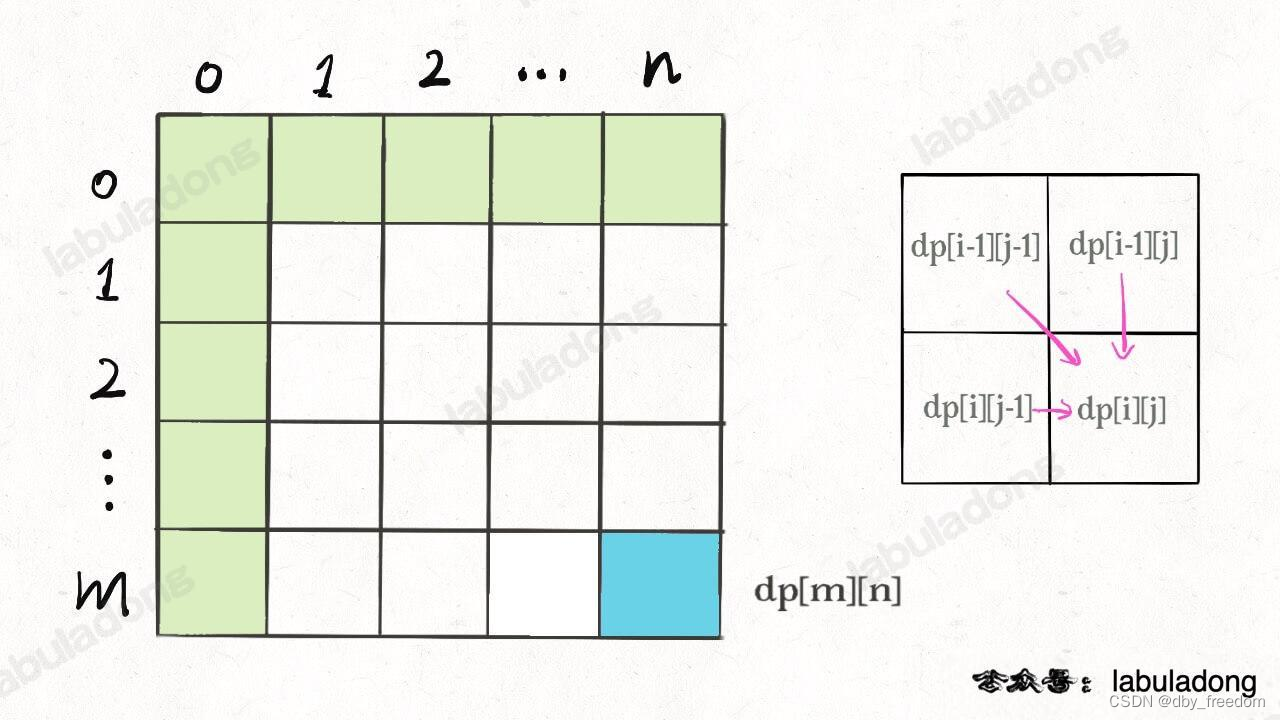
那么,参考刚才说的两条原则,你该怎么遍历 dp 数组?肯定是正向遍历:
for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)// 通过 dp[i-1][j], dp[i][j - 1], dp[i-1][j-1]// 计算 dp[i][j]
因为,这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的,而且最终结束在我们想要的答案 dp[m][n]。
再举一例,回文子序列问题,详见后文 子序列问题模板,我们通过过对 dp 数组的定义,确定了 base case 处在中间的对角线,dp[i][j] 需要从 dp[i+1][j], dp[i][j-1], dp[i+1][j-1] 转移而来,想要求的最终答案是 dp[0][n-1],如下图:
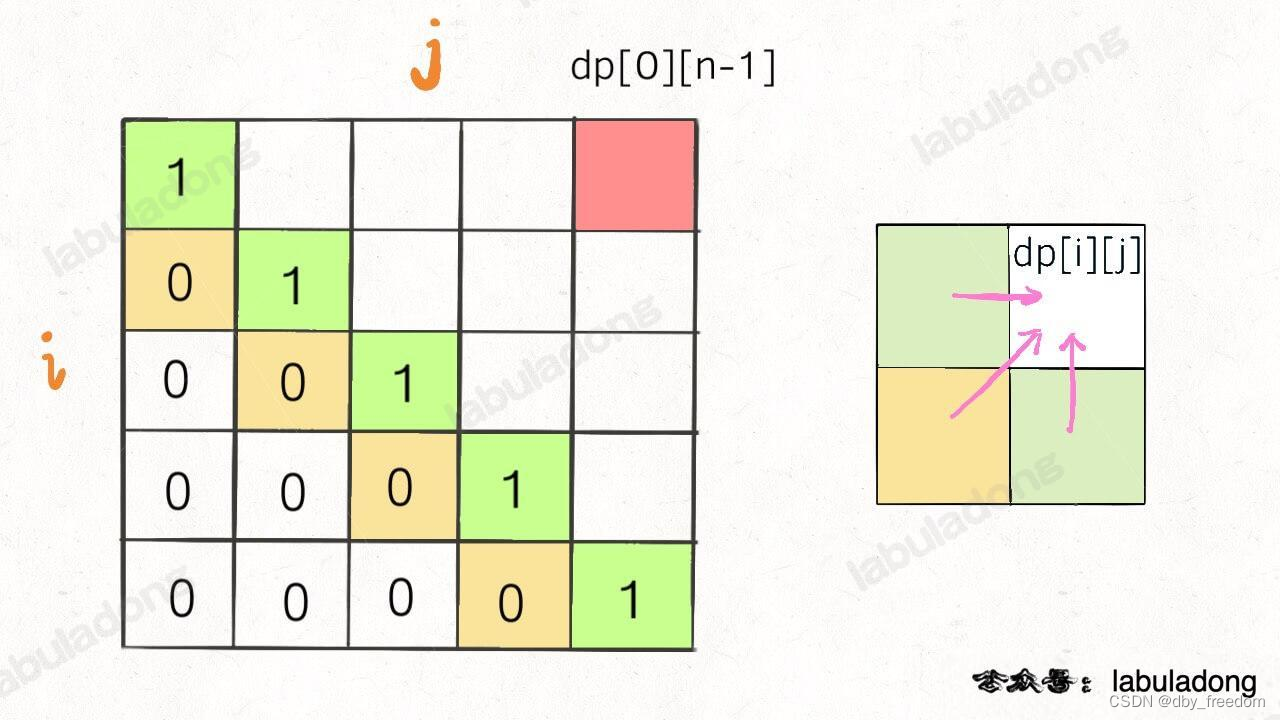
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
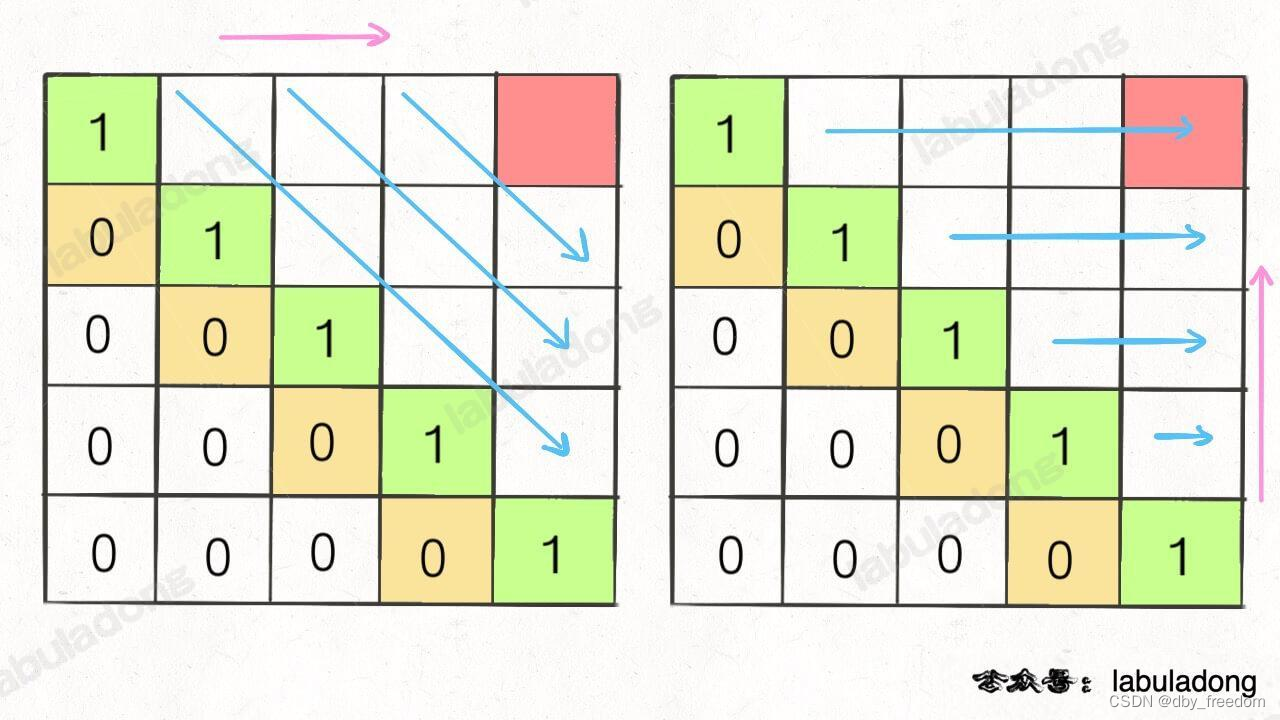
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 dp[i][j] 的左边、下边、左下边已经计算完毕,得到正确结果。
现在,你应该理解了这两个原则,主要就是看 base case 和最终结果的存储位置,保证遍历过程中使用的数据都是计算完毕的就行,有时候确实存在多种方法可以得到正确答案,可根据个人口味自行选择。
注:dp 遍历方向的本质原则就是 以已知推未知,同时需要保证遍历结束时候,存储结果的位置必须已经计算出来;
五、参考文献
- 最优子结构原理和 dp 数组遍历方向
相关文章:

算法与数据结构(二十四)最优子结构原理和 dp 数组遍历方向
注:此文只在个人总结 labuladong 动态规划框架,仅限于学习交流,版权归原作者所有; 本文是两年前发的 动态规划答疑篇open in new window 的修订版,根据我的不断学习总结以及读者的评论反馈,我给扩展了更多…...
Java Vue Uniapp MES生产执行管理系统
本MES系统是一款B/S结构、通用的生产执行管理系统,功能强大! 系统基于多年离散智造行业的业务经验组建,主要目的是为国内离散制造业的中小企业提供一个专业化、通用性、低成本的MES系统解决方案。 联系作者获取...

深入探究Socks5代理与IP代理在网络安全与爬虫中的应用
1. Socks5代理:打开网络隧道的多功能工具 Socks5代理是一种流行的代理协议,它在传输层为数据包提供了隧道。相较于之前的版本,Socks5不仅支持TCP连接,还可以处理UDP流量,使其在需要实时数据传输的应用中表现出色。在网…...
Vue使用jspdf和html2canvas组件库结合导出PDF文件
效果图: 1、安装依赖: npm install html2canvas --save npm install jspdf --save 或 yarn add html2canvas --save yarn add jspdf --save 2、封装全局调用方法:this.$exportPDF(#id,文件名) 新建js文件:/utils/html2Pdf.js&am…...

7. 实现 API 自动生成
目录 1. pom.xml中引用依赖 2. 引入相关的依赖 3. 编写配置类 4. application.yml 中添加配置 5. API 常用注解 6. 访问 API 列表 7. API 导入 Postman 使用 Springfox Swagger生成 API,并导入 Postman,完成API单元测试。 Swagger 简介:Swag…...
使用Druid解析SQL,获取SQL中所有使用的表
一、sqlParse组成 Druid SQL Parser分三个模块: - Parser - AST - Visitor 1.1 Parser parser是将输入文本转换为ast(抽象语法树),parser有包括两个部分,Parser和Lexer,其中Lexer实现词法分析&#x…...

公司内部测试团队可以替代专业的软件检测机构吗,性能测试怎么收费?
第三方软件测试 尽管软件测试是伴随着软件开发的发展而产生的,但是在信息技术日新月异的今天,软件测试逐渐走出开发附庸的定位。 一方面,很多大型企业都在内部设置了专门的测试团队以承接软件系统的测试工作,为产品质量把关。另…...

Three.js之相机、渲染器、光源、动画、性能监测
参考资料 第一个3D案例—透视投影相机第一个3D案例—渲染器…Canvas画布布局和全屏 知识点 透视投影相机PerspectiveCameraWebGL渲染器WebGLRenderer辅助观察坐标系AxesHelper漫反射网格材质MeshLambertMaterial点光源PointLight点光源辅助观察PointLightHelper环境光Ambien…...

Seaborn图表使用指南!
目录 介绍线图散点图直方图概率密度函数 (PDF)箱线图小提琴剧情配对图热图关节图地毯图 一、介绍 数据科学已成为一个突出的领域,近年来呈爆炸性增长。对精通从数据中获取见解并应用这些见解来解决现实世界问题的数据科学家的需求从未增加。…...
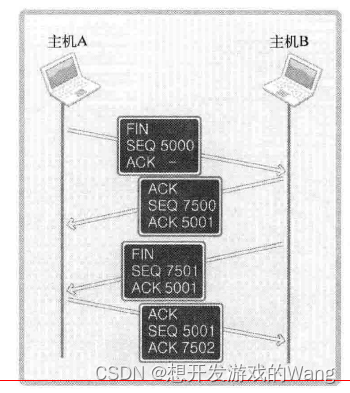
[C++ 网络协议编程] TCP/IP协议
目录 1. TCP/IP协议栈 2. TCP原理 2.1 TCP套接字中的I/O缓冲 2.2 TCP工作原理 2.2.1 三次握手(连接) 2.2.2 与对方主机的数据交换 2.2.3 四次握手(断开与套接字的连接) TCP(Transmission Control Protocol传输控…...

Unity用NPOI创建Exect表,保存数据,和修改删除数据。以及打包后的坑——无法打开新创建的Exect表
先说坑花了一下午才找到解决方法解决, 在Unity编辑模式下点击物体创建对应的表,获取物体名字与在InputText填写的注释数据。然后保存。创建Exect表可以打开,打包PC后,点击物体创建的表,打不开文件破损 解决方法&#…...
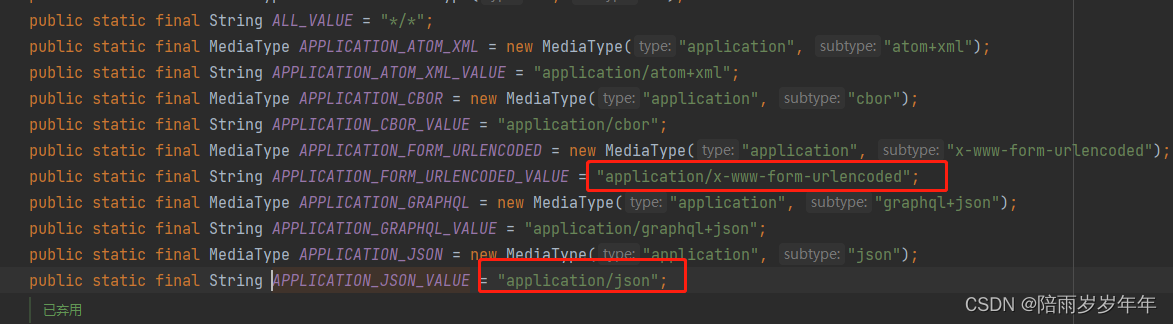
记一次fegin调用的媒体类型问题
1.问题:分页查询,分页参数传递不生效 2.开发环境:fegin接口 开发环境:调用接口 3.修改后:fegin接口不变 调用接口 前端媒体类型: 问题解决!!! 4.原因分析&…...
)
在Hive/Spark上运行执行TPC-DS基准测试 (ORC和TEXT格式)
目前,在Hive/Spark上运行TPC-DS Benchmark主要是通过早期由Hortonworks维护的一个项目:hive-testbench 来完成的。本文我们以该项目为基础介绍一下具体的操作步骤。不过,该项目仅支持生成ORC和TEXT格式的数据,如果需要Parquet格式,请参考此文《在Hive/Spark上执行TPC-DS基…...
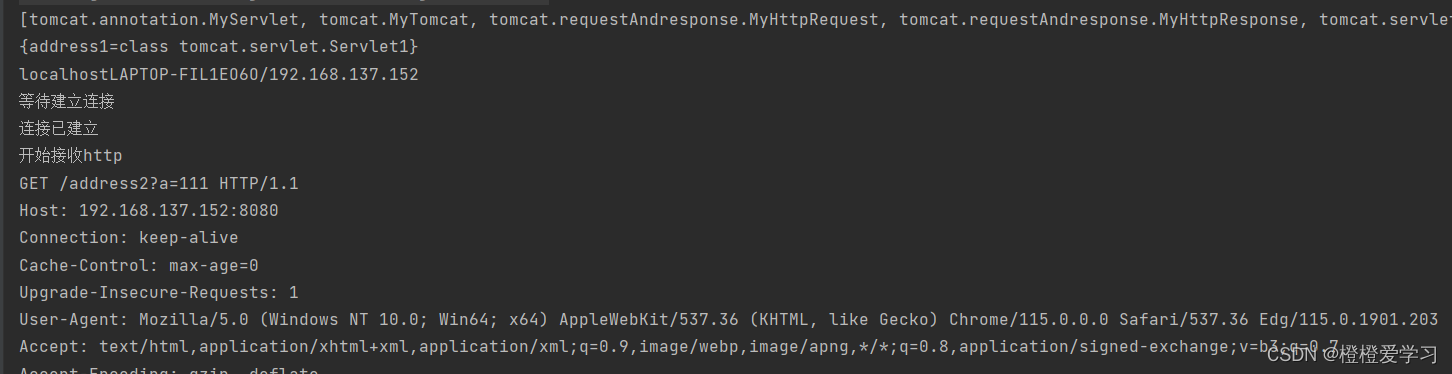
如何仿写简易tomcat 实现思路+代码详细讲解
仿写之前,我们要搞清楚都要用到哪些技术 自定义注解,比如Tomcat使用的是Servlet,我们可以定义一个自己的MyServlet构造请求体和返回体,比如tomcat使用HttpRequest,我们可以自己定义myHttpRequestjava去遍历一个指定目…...

如何提高深度学习性能
可用于 对抗过度拟合并获得更好泛化能力的20 个提示、技巧和技术 如何从深度学习模型中获得更好的性能? 这是我最常被问到的问题之一。 可能会被问为: 如何提高准确率? ……或者可以反过来说: 如果我的神经网络表现不佳该怎么办? 我经常回答说:“我不太清楚,但我有很…...

ECMAScript版本对比:从ES1到ES2021
引言 ECMAScript(简称ES)是一种用于编写Web前端JavaScript的标准化语言。自1997年发布第一版(ES1)以来,ECMAScript已经经历了多个版本的更新和演进。每个版本都引入了新的语法和功能,为开发人员提供了更强…...

设计HTML5表格
在网页设计中,表格主要用于显示包含行、列结构的二维数据,如财务表格、调查数据、日历表、时刻表、节目表等。在大多数情况下,这类信息都由列标题或行标题及数据构成。本章将详细介绍表格在网页设计中的应用,包括设计符合标准化的…...

神经网络基础-神经网络补充概念-60-卷积步长
概念 在深度学习中,卷积步长(convolution stride)是指在卷积操作中滑动卷积核的步幅。卷积操作是神经网络中常用的操作之一,用于从输入数据中提取特征。步长决定了卷积核在输入数据上的滑动间隔,从而影响输出特征图的…...

怎么开通Tik Tok海外娱乐公会呢?
TikTok作为全球知名的社交媒体平台,吸引了数亿用户的关注和参与。许多公司和个人渴望通过开通TikTok直播公会进入这一领域,以展示自己的创造力和吸引更多粉丝。然而,成为TikTok直播公会并非易事,需要满足一定的门槛和申请找cmxyci…...

Java接口压力测试—如何应对并优化Java接口的压力测试
导言 在如今的互联网时代,Java接口压力测试是评估系统性能和可靠性的关键一环。一旦接口不能承受高并发量,用户体验将受到严重影响,甚至可能导致系统崩溃。因此,了解如何进行有效的Java接口压力测试以及如何优化接口性能至关重要…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
