160. 相交链表
题目描述
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交**:**

题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:

输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:

输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:

输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
**进阶:**你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
解答
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {// pA 和 pB先走A链表和B链表,然后再切换另一个链表走,有交点就能找到// 没交点最后两指针都同时到nullptrListNode *pA = headA, *pB = headB;while(pA != pB){pA = (pA == NULL ? headB : pA->next);pB = (pB == NULL ? headA : pB->next);}return pA;}
};
相关文章:

160. 相交链表
题目描述 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 图示两个链表在节点 c1 开始相交**:** 题目数据 保证 整个链式结构中不存在环。 注意,函…...

【MFC】12.双缓冲序列化机制-笔记
双缓冲 双缓冲在之前写字符雨的时候,已经简单介绍过,今天我们来写一个简单的程序来体会双缓冲机制 我们实现一个在屏幕上画直线的功能: 在类中添加变量,保存起点坐标和终点坐标: //定义一个容器,保存每…...

Linux 终端会话中,启动任务并放到后台运行
一、需求 linux要执行一个脚本,耗时很长,想要脚本在后台运行,用户注销或终端软件关闭时也可以继续运行。 二、实现 1、nohup命令 脚本在后台运行 nohup 是在 Linux 和类 Unix 系统中使用的一个命令,用于在后台运行程序&#x…...
软考笔记——10.项目管理
进度管理 进度管理就是采用科学的方法,确定进度目标,编制进度计划和资源供应计划,进行进度控制,在与质量、成本目标协调的基础上,实现工期目标。 具体来说,包括以下过程: (1) 活动定义&#…...
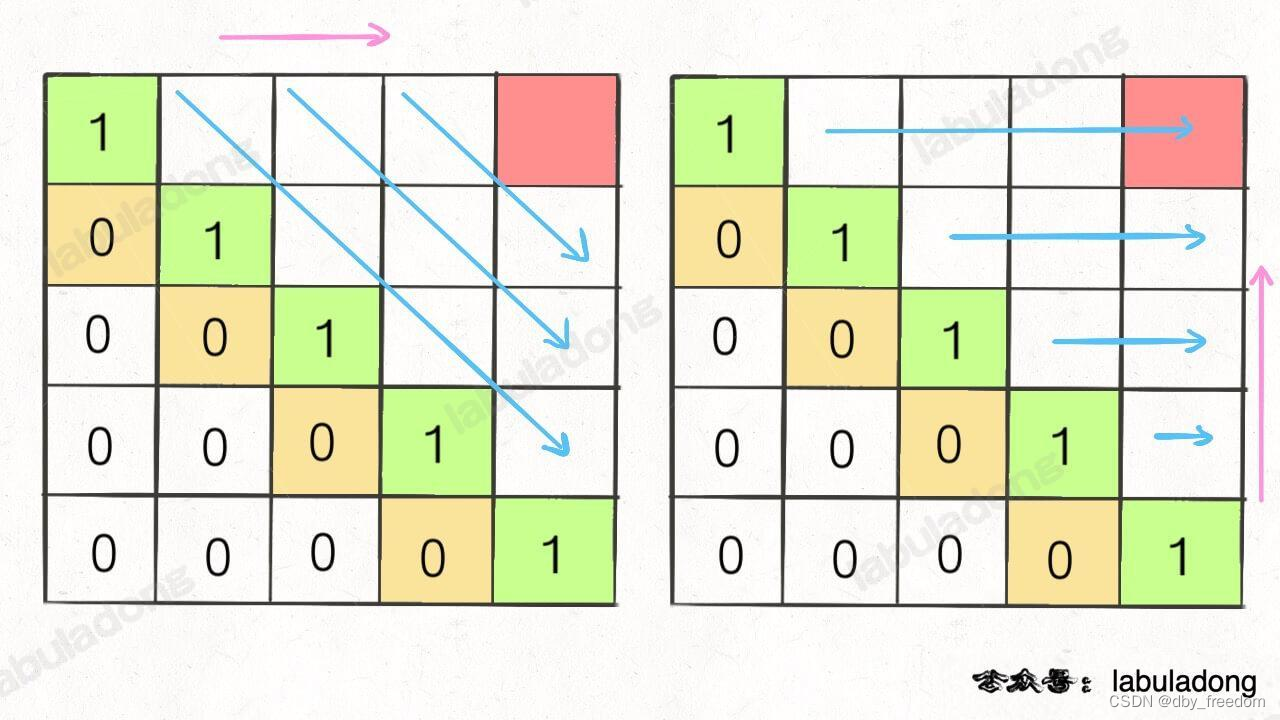
算法与数据结构(二十四)最优子结构原理和 dp 数组遍历方向
注:此文只在个人总结 labuladong 动态规划框架,仅限于学习交流,版权归原作者所有; 本文是两年前发的 动态规划答疑篇open in new window 的修订版,根据我的不断学习总结以及读者的评论反馈,我给扩展了更多…...
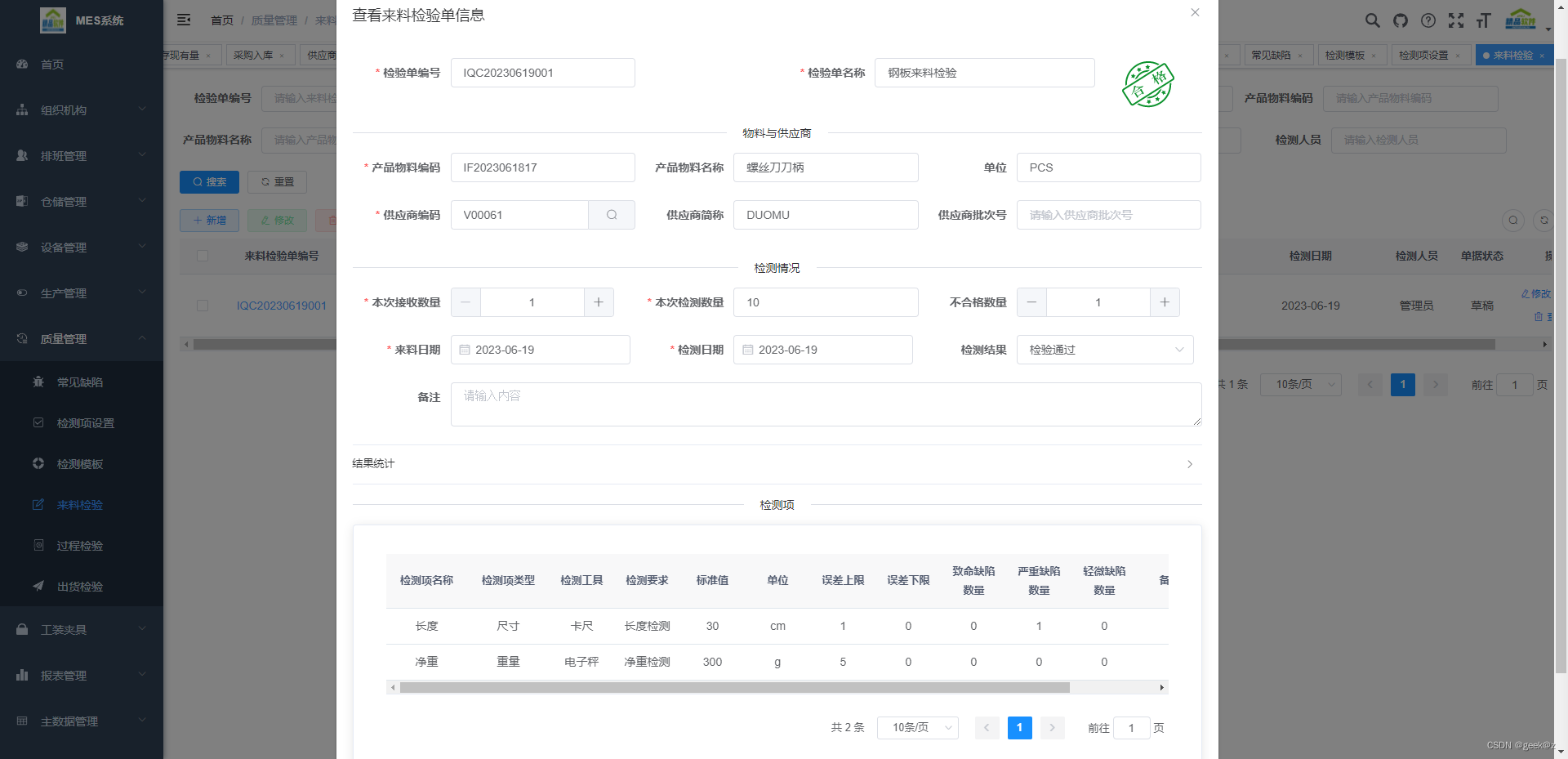
Java Vue Uniapp MES生产执行管理系统
本MES系统是一款B/S结构、通用的生产执行管理系统,功能强大! 系统基于多年离散智造行业的业务经验组建,主要目的是为国内离散制造业的中小企业提供一个专业化、通用性、低成本的MES系统解决方案。 联系作者获取...

深入探究Socks5代理与IP代理在网络安全与爬虫中的应用
1. Socks5代理:打开网络隧道的多功能工具 Socks5代理是一种流行的代理协议,它在传输层为数据包提供了隧道。相较于之前的版本,Socks5不仅支持TCP连接,还可以处理UDP流量,使其在需要实时数据传输的应用中表现出色。在网…...
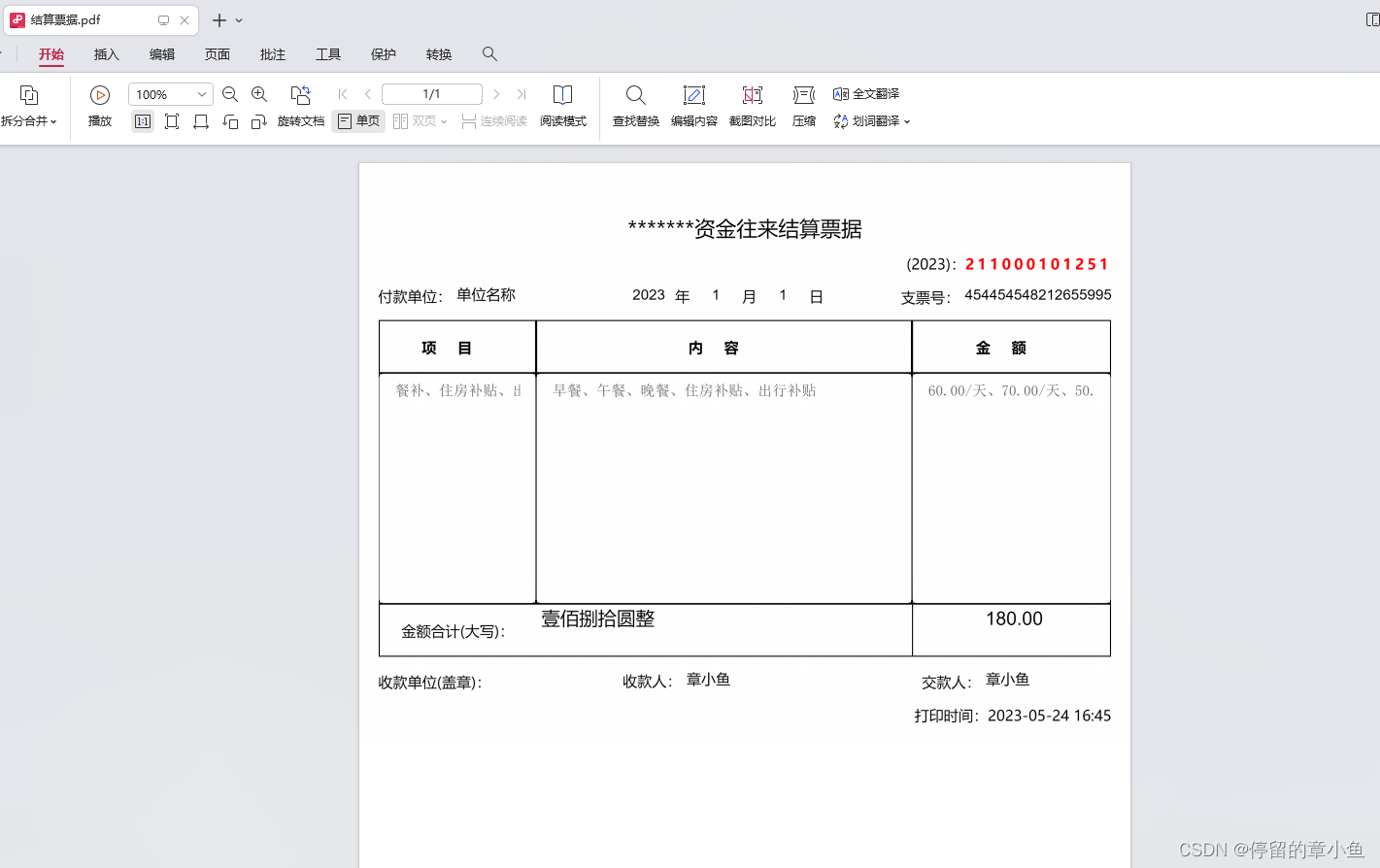
Vue使用jspdf和html2canvas组件库结合导出PDF文件
效果图: 1、安装依赖: npm install html2canvas --save npm install jspdf --save 或 yarn add html2canvas --save yarn add jspdf --save 2、封装全局调用方法:this.$exportPDF(#id,文件名) 新建js文件:/utils/html2Pdf.js&am…...

7. 实现 API 自动生成
目录 1. pom.xml中引用依赖 2. 引入相关的依赖 3. 编写配置类 4. application.yml 中添加配置 5. API 常用注解 6. 访问 API 列表 7. API 导入 Postman 使用 Springfox Swagger生成 API,并导入 Postman,完成API单元测试。 Swagger 简介:Swag…...
使用Druid解析SQL,获取SQL中所有使用的表
一、sqlParse组成 Druid SQL Parser分三个模块: - Parser - AST - Visitor 1.1 Parser parser是将输入文本转换为ast(抽象语法树),parser有包括两个部分,Parser和Lexer,其中Lexer实现词法分析&#x…...

公司内部测试团队可以替代专业的软件检测机构吗,性能测试怎么收费?
第三方软件测试 尽管软件测试是伴随着软件开发的发展而产生的,但是在信息技术日新月异的今天,软件测试逐渐走出开发附庸的定位。 一方面,很多大型企业都在内部设置了专门的测试团队以承接软件系统的测试工作,为产品质量把关。另…...

Three.js之相机、渲染器、光源、动画、性能监测
参考资料 第一个3D案例—透视投影相机第一个3D案例—渲染器…Canvas画布布局和全屏 知识点 透视投影相机PerspectiveCameraWebGL渲染器WebGLRenderer辅助观察坐标系AxesHelper漫反射网格材质MeshLambertMaterial点光源PointLight点光源辅助观察PointLightHelper环境光Ambien…...

Seaborn图表使用指南!
目录 介绍线图散点图直方图概率密度函数 (PDF)箱线图小提琴剧情配对图热图关节图地毯图 一、介绍 数据科学已成为一个突出的领域,近年来呈爆炸性增长。对精通从数据中获取见解并应用这些见解来解决现实世界问题的数据科学家的需求从未增加。…...
[C++ 网络协议编程] TCP/IP协议
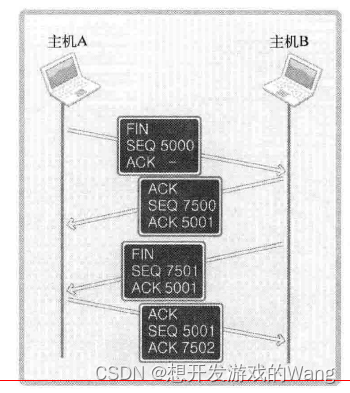
目录 1. TCP/IP协议栈 2. TCP原理 2.1 TCP套接字中的I/O缓冲 2.2 TCP工作原理 2.2.1 三次握手(连接) 2.2.2 与对方主机的数据交换 2.2.3 四次握手(断开与套接字的连接) TCP(Transmission Control Protocol传输控…...

Unity用NPOI创建Exect表,保存数据,和修改删除数据。以及打包后的坑——无法打开新创建的Exect表
先说坑花了一下午才找到解决方法解决, 在Unity编辑模式下点击物体创建对应的表,获取物体名字与在InputText填写的注释数据。然后保存。创建Exect表可以打开,打包PC后,点击物体创建的表,打不开文件破损 解决方法&#…...
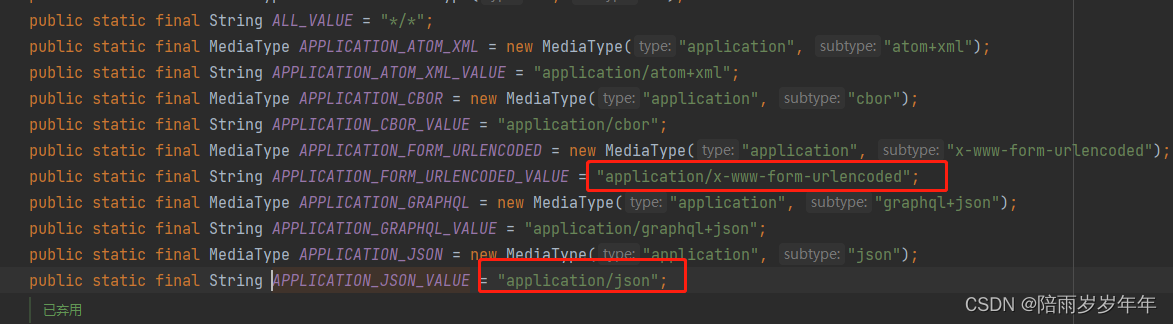
记一次fegin调用的媒体类型问题
1.问题:分页查询,分页参数传递不生效 2.开发环境:fegin接口 开发环境:调用接口 3.修改后:fegin接口不变 调用接口 前端媒体类型: 问题解决!!! 4.原因分析&…...
)
在Hive/Spark上运行执行TPC-DS基准测试 (ORC和TEXT格式)
目前,在Hive/Spark上运行TPC-DS Benchmark主要是通过早期由Hortonworks维护的一个项目:hive-testbench 来完成的。本文我们以该项目为基础介绍一下具体的操作步骤。不过,该项目仅支持生成ORC和TEXT格式的数据,如果需要Parquet格式,请参考此文《在Hive/Spark上执行TPC-DS基…...
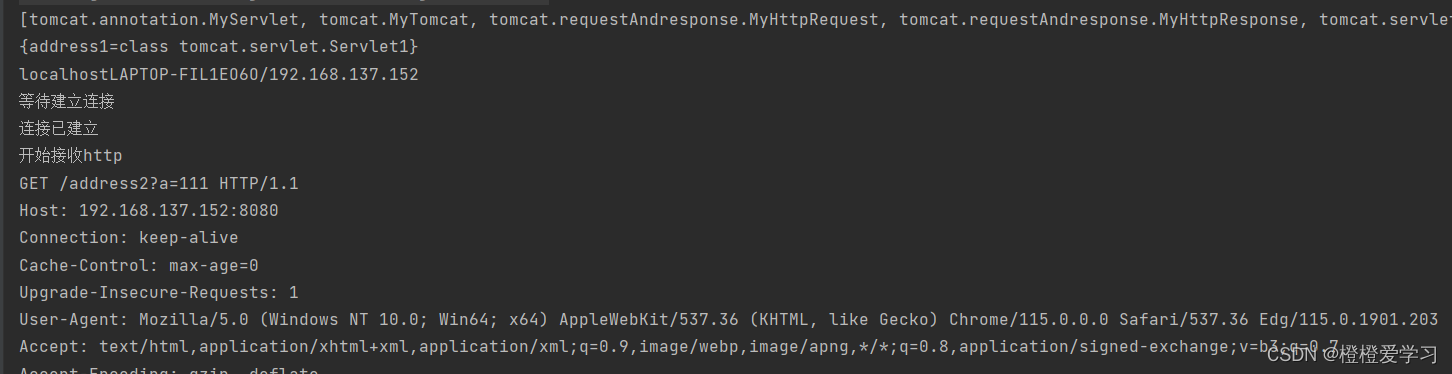
如何仿写简易tomcat 实现思路+代码详细讲解
仿写之前,我们要搞清楚都要用到哪些技术 自定义注解,比如Tomcat使用的是Servlet,我们可以定义一个自己的MyServlet构造请求体和返回体,比如tomcat使用HttpRequest,我们可以自己定义myHttpRequestjava去遍历一个指定目…...

如何提高深度学习性能
可用于 对抗过度拟合并获得更好泛化能力的20 个提示、技巧和技术 如何从深度学习模型中获得更好的性能? 这是我最常被问到的问题之一。 可能会被问为: 如何提高准确率? ……或者可以反过来说: 如果我的神经网络表现不佳该怎么办? 我经常回答说:“我不太清楚,但我有很…...

ECMAScript版本对比:从ES1到ES2021
引言 ECMAScript(简称ES)是一种用于编写Web前端JavaScript的标准化语言。自1997年发布第一版(ES1)以来,ECMAScript已经经历了多个版本的更新和演进。每个版本都引入了新的语法和功能,为开发人员提供了更强…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
