matlab使用教程(17)—多项式的定义和运算
1.创建并计算多项式
1.1 表示多项式
1.2 多项式的计算
将变为矩阵表达式
2.多项式的根
2.1 数值根
2.2 使用代换法求根
2.3 特定区间内的根


2.4 符号根
3.对多项式求积分和微分

 生成的多项式为
生成的多项式为 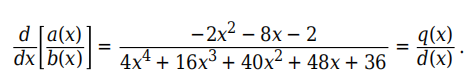
相关文章:
matlab使用教程(17)—多项式的定义和运算
1.创建并计算多项式 此示例说明如何在 MATLAB 中将多项式表示为向量以及根据相关点计算多项式。 1.1 表示多项式 MATLAB 将多项式表示为行向量,其中包含按降幂排序的系数。例如,三元素向量 p [p2 p1 p0]; 表示多项式 创建一个向量以表示二次多项式…...

华为认证 | 这门HCIA认证正式发布!
华为认证云服务工程师HCIA-Cloud Service V3.5(中文版)自2023年8月11日起,正式在中国区发布。 01 发布概述 基于“平台生态”战略,围绕“云-管-端”协同的新ICT技术架构,华为公司打造了覆盖ICT领域的认证体系…...
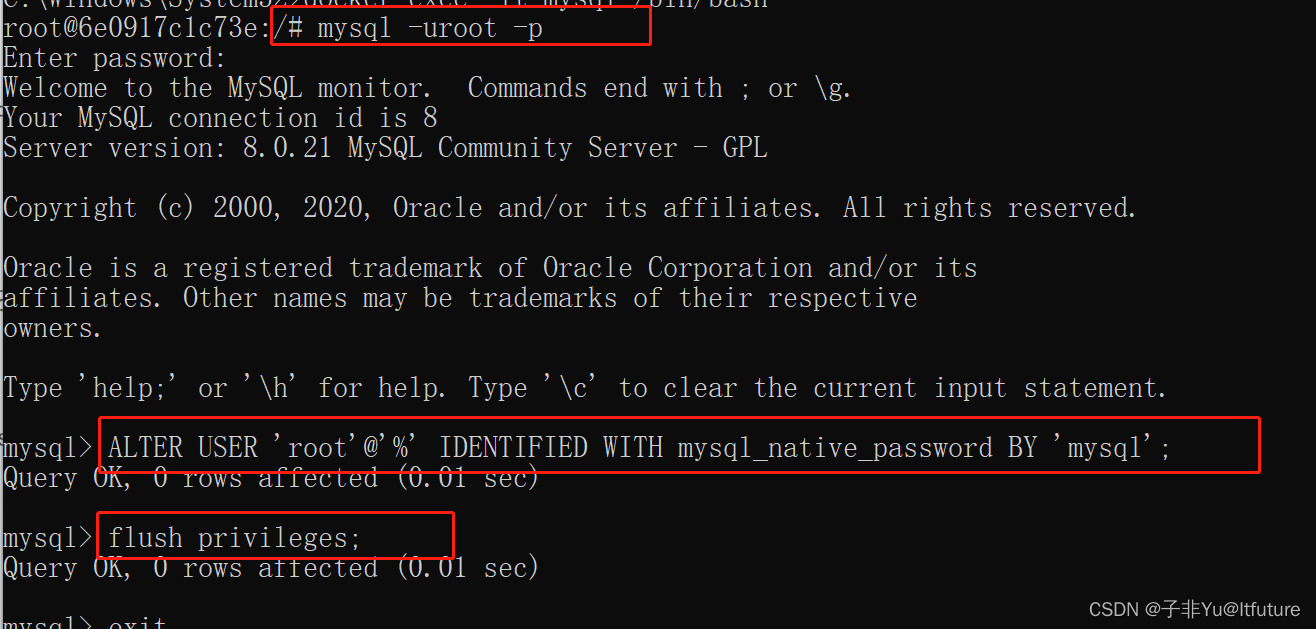
【Docker】Docker安装 MySQL 8.0,简洁版-快速安装使用
今天,使用docker安装mysql数据库进行一个测试,结果网上找了一篇文章,然后。。。。坑死我… 特总结本篇安装教程,主打一个废话不多说! 坑:安装成功,客户端工具连接不上数据库》。。。 正文&…...

CSS自己实现一个步骤条
前言 步骤条是一种用于引导用户按照特定流程完成任务的导航条,在各种分步表单交互场景中广泛应用。例如:在HIS系统-门诊医生站中的接诊场景中,我们就可以使用步骤条来实现。她的执行步骤分别是:门诊病历>遗嘱录入>完成接诊…...
Visual Studio 2019 解决scanf函数报错问题
前言 Visual Studio 2019 解决scanf函数报错问题 博主博客链接:https://blog.csdn.net/m0_74014525 关注博主,后期持续更新系列文章 *****感谢观看,希望对你有所帮助***** 系列文章 第一篇:Visual Studio 2019 详细安装教程&…...
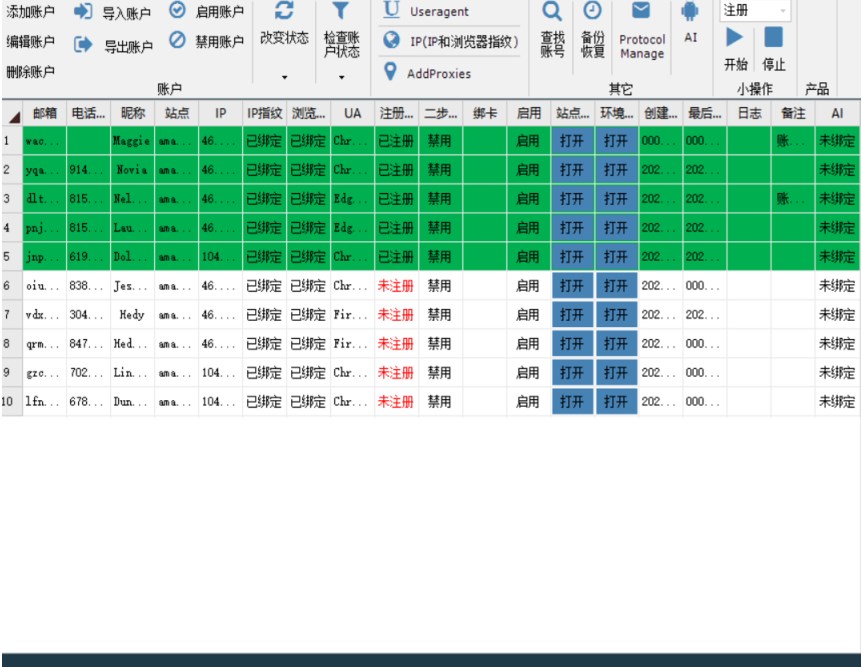
亚马逊无限买家号如何注册?
如果想要拥有大批量的亚马逊买家号,可以使用亚马逊鲲鹏系统进行自动注册操作。在注册之前我们需要先准备好账号所需要的资料; 1、Ip:软件系统支持11个亚马逊站点使用,因此注册哪一个国家的买家号时就需要购买相应国家的ip&#x…...
)
前端框架学习-ES6新特性(尚硅谷web笔记)
ECMASript是由 Ecma 国际通过 ECMA-262 标准化的脚本程序设计语言。javaScript也是该规范的一种实现。 新特性目录 笔记出处:b站ES6let 关键字const关键字变量的解构赋值模板字符串简化对象写法箭头函数rest参数spread扩展运算符Promise模块化 ES8async 和 await E…...

普陀发布新规服务元宇宙企业 和数软件发展元宇宙场景落地
近日,数智中国AIGC科技周2023全球元宇宙大会上海站活动现场“半马苏河”元宇宙企业科创政策包正式发布。政策包在普陀原有科创政策基础上进行了叠加升级,一共涵盖了十条专项服务元宇宙企业的专项政策,简称普陀“元十条”。 普陀“元十条”从…...

Kotlin差异化分析,let,run,with,apply及also
作用域函数是Kotlin比较重要的一个特性,共分为以下5种:let、run、with、apply 以及 also,这五个函数的工作方式可以说非常相似,但是我们需要了解的是这5种函数的差异,以便在不同的场景更好的利用它。 读完这篇文章您将…...

(stm32)低功耗模式
低功耗模式 执行哪个低功耗模式的程序判断流程 标志位设置操作一定要在WFI/WFE之前,调用此指令后立即进入睡眠判断流程 模式对比 睡眠模式 停止模式 待机模式...

【C++学习手札】一文带你认识C++虚函数(内层剖析)
食用指南:本文在有C基础的情况下食用更佳 🍀本文前置知识: C初识继承 ♈️今日夜电波:No title —REOL 1:02 ━━━━━━️💟──────── 4:03 …...
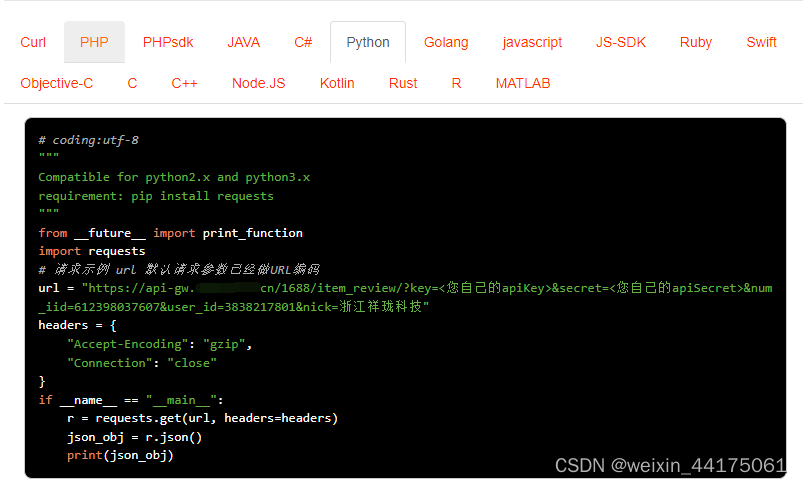
Python“牵手”1688商品评论数据采集方法,1688API申请指南
1688平台API接口是为开发电商类应用程序而设计的一套完整的、跨浏览器、跨平台的接口规范,1688API接口是指通过编程的方式,让开发者能够通过HTTP协议直接访问1688平台的数据,包括商品信息、店铺信息、物流信息等,从而实现1688平台…...

“深入解析JVM内部机制:探秘Java虚拟机的奥秘“
标题:深入解析JVM内部机制:探秘Java虚拟机的奥秘 摘要:本文将深入解析JVM(Java虚拟机)的内部机制,从字节码执行到垃圾回收,逐步揭示Java程序运行的奥秘。通过理论分析和示例代码,读…...
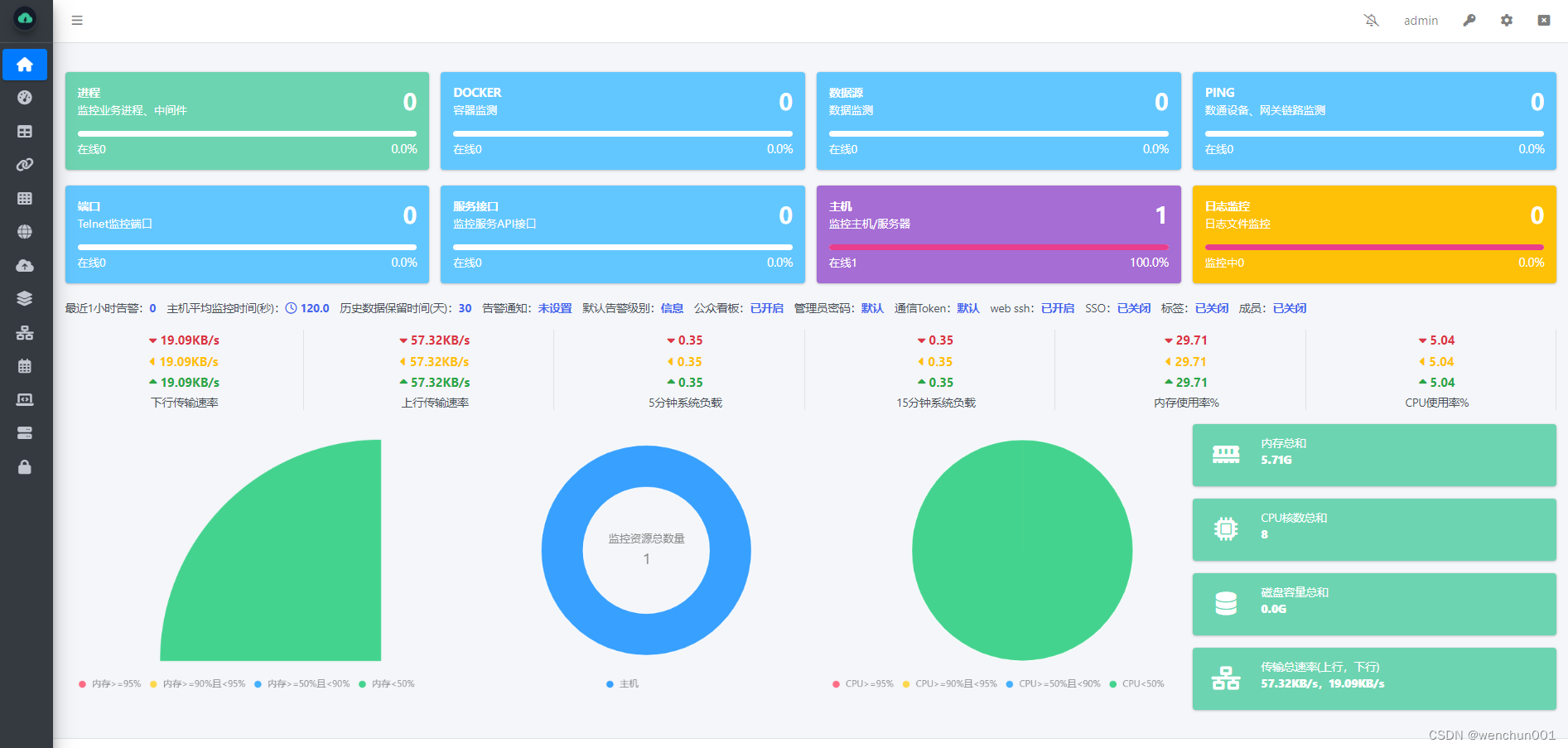
【系统工具】开源服务器监控工具WGCLOUD初体验
经常看到服务器上传下载流量一直在跑,也不知道是啥软件在偷偷联网~~~官网地址:www.wgstart.com,个人使用是免费的。 WGCLOUD官网介绍 "WGCLOUD支持主机各种指标监测(cpu使用率,cpu温度,内存使用率&am…...

powerBI应用技巧
power BI应用技巧 持续跟新 1.函数日期表 使用高级编辑器—M函数(把下面代码直接复制即可) 版本1:前单位写的M函数,日期是2021年开始的 letdate(optional 请输入开始年份 as number,optional 请输入结束年份 as number)>l…...

RK3568背光调试分享
一.PWM 驱动 驱动文件所在位置: drivers/pwm/pwm-rockchip.c 3.10 和 4.4 及以上版本内核下驱动文件名字是同一个, pwm-rockchip.c 只支持 Continuous mode , 但是里面的代码有些差别。 4.4 及以上内核版本将 pwm_config() , pwm_enable()...
—随机数)
Numpy入门(2)—随机数
随机数np.random 主要知识点: 创建ndarray随机数组随机打乱ndarray元素顺序随机选取元素 2.1 创建随机ndarray数组 创建随机ndarray数组主要包含设置随机种子、均匀分布和正态分布三部分内容,具体代码如下所示。 设置随机数种子 # 可以多次运行&am…...
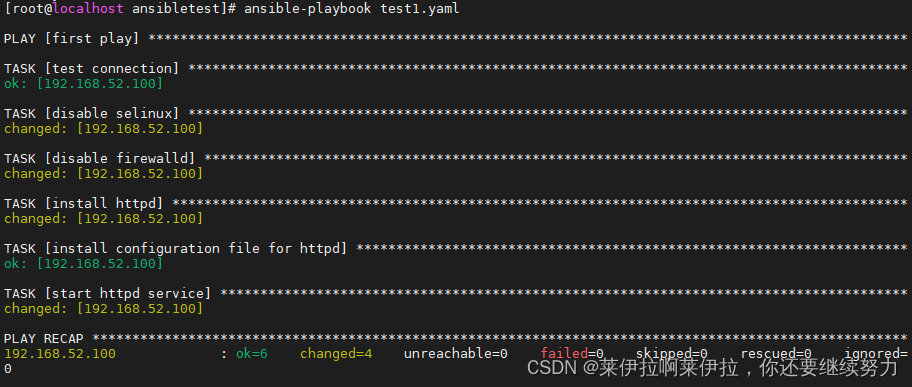
ansible的playbook剧本
playbook剧本 PlayBook1.playbooks 本身由以下各部分组成2.示例:3.运行playbook补充参数: 4.定义、引用变量5.指定远程主机sudo切换用户6.when条件判断7.迭代8.Templates 模块1.先准备一个以 .j2 为后缀的 template 模板文件,设置引用的变量2…...

【03 英语语法:从句(名词从句、定语从句/形容词从句、状语从句/副词从句)】
从句 从句:名词从句、定语从句、状语从句(名定状名形副)1. 名词从句(名词):主语、宾语、表语、同位语、宾补▲名词从句的种类(按引导词): that、whether、疑问词 句子⑴…...
vue动态修改audio地址
问题:点击后替换url地址,实现了,但是播放器依旧没有反应。 解决:vue中动态替换只是替换了地址,并没有告诉audio标签是否要执行,执行什么操作。要load后才能让它知道,是在喊他,他需求…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
