数据结构:二叉树的递归实现(C实现)

个人主页 : 个人主页
个人专栏 : 《数据结构》 《C语言》
文章目录
- 前言
- 一、树的概念
- 二、二叉树
- 二叉树的概念
- 二叉树的性质
- 三、二叉树链式结构实现
- 二叉树节点定义
- 创建二叉树节点
- 遍历二叉树
- 先序遍历二叉树(BinaryTreePrevOrder)
- 中序遍历二叉树(BinaryTreeInOrder)
- 后序遍历二叉树(BinaryTreePostOrder)
- 层序遍历二叉树(BinaryTreeLevelOrder)
- 二叉树节点个数(BinaryTreeSize)
- 二叉树第K层节点个数(BinaryTreeLevelKSize)
- 二叉树叶子节点个数(BinaryTreeLeafSize)
- 二叉树查找值为X的节点(BinaryTreeFind)
- 判断二叉树是否是完全二叉树(BinaryTreeComplete)
- 通过前序遍历的数组构建二叉树
- 四、代码展示
- 二叉树代码展示
- 队列代码展示
- 总结
前言
本篇博客主要讲解二叉树的相关操作如下:
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);//二叉树的销毁
void BinaryTreeDestroy(BTNode* root);//二叉树节点个数
int BinaryTreeSize(BTNode* root);//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉树查找值为X的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);//二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);//二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);//层序遍历
void BinaryTreeLevelOrder(BTNode* root);//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x);
一、树的概念
树是一种非线性结构,它是由n个有限节点组成的一个有层次关系的集合。

- 图中A节点没有前驱节点,被称为根节点
- 除根节点外,其余节点被分成两个无不相交的集合T1(B,D,E,F…),T2(C,G,H,L…)。其中每个集合T又是一颗结构与树类似的子树。每一颗子树的根节点有且只有一个根节点,可以有0个或多个后继节点
- 因此,树是递归定义的。
- 树的子树不能有交集,否则就为图。
- 节点的度:一个节点含有的子树的个数称为该节点的度;如上图A节点的度是2
- 叶节点或终端节点:度为0的节点被称为叶节点;如上图:K,J,F,L,O,P为叶节点
- 非终端节点或分支节点:度不为0的节点;如上图:A,B,C,D,E…等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。如上图A节点是B,C的父节点
- 孩子节点或子节点:若一个节点含有子树,则子树的根节点就是该节点的子节点。如上图B,C是A的子节点
- 兄弟节点:具有相同的父节点的节点互为兄弟节点。如上图B,C互为兄弟节点
- 树的度:一颗树中,最大节点的度就是该数的度。如上图数的度为3
- 节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,依次类推。如上图G节点的层次为3
- 树的高度或深度:树中节点的最大层次。如上图树的深度为5
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟节点。如上图D,G互为堂兄弟节点
- 节点的祖先:从根到该节点所经分支上的所以节点。如上图A是所以节点的祖先
- 子孙节点 :以某节点为根的子树中任一节点都称为该节点的子孙。如上图所以节点是A的子孙
- 森林:由m棵互不相交的树的集合称为森林
二、二叉树
二叉树的概念
由一个根节点加上两颗子树构成 。

- 二叉树的度最大为2
- 二叉树是有序树,二叉树的子树有左右之分,次序不能颠倒
二叉树的性质
若规定根节点的层数是1,则一个非空二叉树的第K层最多有2^(k - 1)个节点
若规定根节点的层数是1,则深度为h的二叉树的最大节点数是2^h - 1
对于任何一颗二叉树,如果度为0的节点为N0,度为2的节点为N2,那么N0 = N2 + 1 (数学归纳)
若规定根节点的层数是1,具有N个节点的满二叉树的深度为log(n + 1)[以2为底]
对于具有n个节点的完全二叉树,如果按照从上至下从左到右的数组顺序对所以节点从0开始编号(也就是堆的结构),则对序号为K的节点有:
若k>0,k节点的父节点的序号:(k - 1) / 2;
如果k是0(根节点),则无父节点
若2k+1<n,左孩子序号 2k+1,右孩子序号2k+2 如果2k+1> n则无左孩子 2*k+2>n则无右孩子
三、二叉树链式结构实现
二叉树节点定义
节点需要一个数据域,一个指向左孩子节点的指针,一个指向右孩子节点的指针。
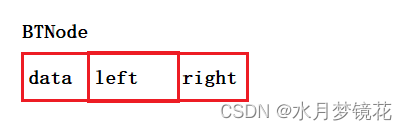
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
创建二叉树节点
我们只需要传递二叉树节点的数据即可,动态开辟出的节点空间用返回值的方式接受。
malloc出一块节点空间,将函数参数给data,使left 和 right 指向NULL,返回该空间的地址

//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc:");exit(-1);}root->data = x;root->left = root->right = NULL;return root;
}
为了方便我们理解,这里我们先手动创建一个二叉树来进行讲解相关操作,最后在来讲解先序创建二叉树。
void test()
{BTNode* a = BuyBinaryTreeNode('A');BTNode* b = BuyBinaryTreeNode('B');BTNode* c = BuyBinaryTreeNode('C');BTNode* d = BuyBinaryTreeNode('D');BTNode* e = BuyBinaryTreeNode('E');BTNode* f = BuyBinaryTreeNode('F');BTNode* g = BuyBinaryTreeNode('G');BTNode* h = BuyBinaryTreeNode('H');a->left = b;b->left = d;b->right = e;e->right = h;a->right = c;c->left = f;c->right = g;
}
创建的二叉树就是下图所示:
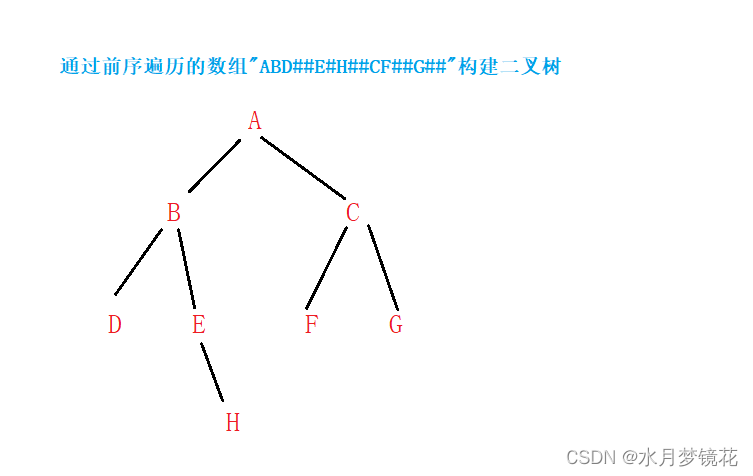
遍历二叉树
遍历二叉树有多种方式:
- 先序遍历 :根节点 -> 左子树 -> 右子树
- 中序遍历 :左子树-> 根节点 -> 右子树
- 后序遍历 :左子树 -> 右子树 -> 根节点
- 层序遍历 : 从左到右从上到下,依次遍历二叉树节点
先序遍历二叉树(BinaryTreePrevOrder)
对于下图中的二叉树,其先序遍历结果为:ABD##E#H##CF##G##( ’ # ’ 表示NULL )
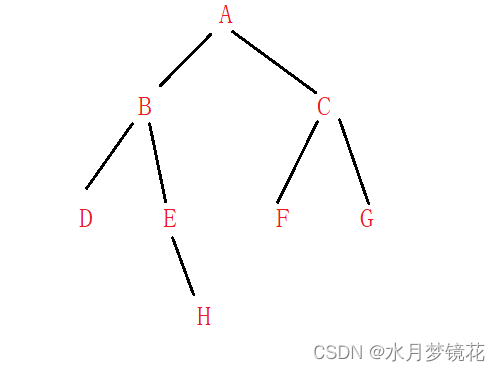
那么是如何遍历的?我们需要按照根,左,右的顺序递归二叉树即可。

//二叉树前序遍历 根节点 左子树 右子树
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//根节点printf("%c ", root->data);//左子树BinaryTreePrevOrder(root->left);//右子树BinaryTreePrevOrder(root->right);
}
这份代码是如何展开的?

中序遍历二叉树(BinaryTreeInOrder)
中序遍历与先序遍历类似,只有将根节点的访问与左子树递归交换执行顺序即可
对于下图中的二叉树,其中序遍历结果为:#D#B#E#H#A#F#C#G# ( ’ # ’ 表示NULL )

//二叉树中序遍历 左子树 根 右子树
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreeInOrder(root->left);//根printf("%c ", root->data);//右子树BinaryTreeInOrder(root->right);
}
后序遍历二叉树(BinaryTreePostOrder)
后序遍历,就是再次调整根节点的访问顺序,将根节点的访问顺序调整到左子树递归与右子树递归后即可。
对于下图中的二叉树,其中序遍历结果为:##D###HEB##F##GCA ( ’ # ’ 表示NULL )

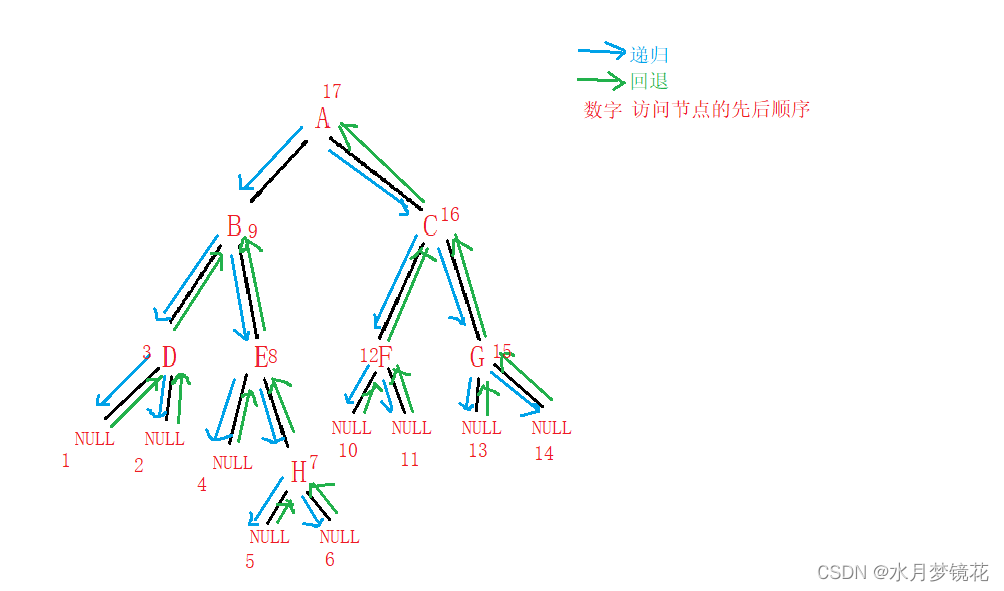
//二叉树后序遍历 左子树 右子树 根
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreePostOrder(root->left);//右子树BinaryTreePostOrder(root->right);//根printf("%c ", root->data);
}
层序遍历二叉树(BinaryTreeLevelOrder)
要实现二叉树的层序遍历,我们需要借助队列。
我们将根节点先入队列,之后我们每次出队头数据时,将该队头数据指向的左子节点 与 右子节点分别入队列,如果左子节点 或 右子节点 为NULL就不入队列,重复上述过程直到队列为空

//层序遍历 借助队列 出队头数据时,将其左子节点 与 右子节点依次入队列
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);//入根节点QuenePush(&q, root);//队列为空,代表二叉树中元素也遍历完成while (!QueneEmpty(&q)){QDataType val = QueneFront(&q);printf("%c ", val->data);//入数据 该节点的左节点 与 右节点if (val->left != NULL)QuenePush(&q, val->left);if (val->right != NULL)QuenePush(&q, val->right);//出队头数据QuenePop(&q);}QueneDestrory(&q);
}
二叉树节点个数(BinaryTreeSize)
我们使用递归的思路来看待二叉树节点个数的接口。
子问题:根节点的左子树的节点个数 与 根节点的右子树的节点个数
结束条件:空节点返回
所以求二叉树节点个数的问题可以转换为求根节点左子树节点数 + 根节点右子树节点数 +根节点的节点总数
//二叉树节点个数 根节点的左子树与右子树的节点个数和
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}// 左子树节点数 右子树节点数 根节点return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
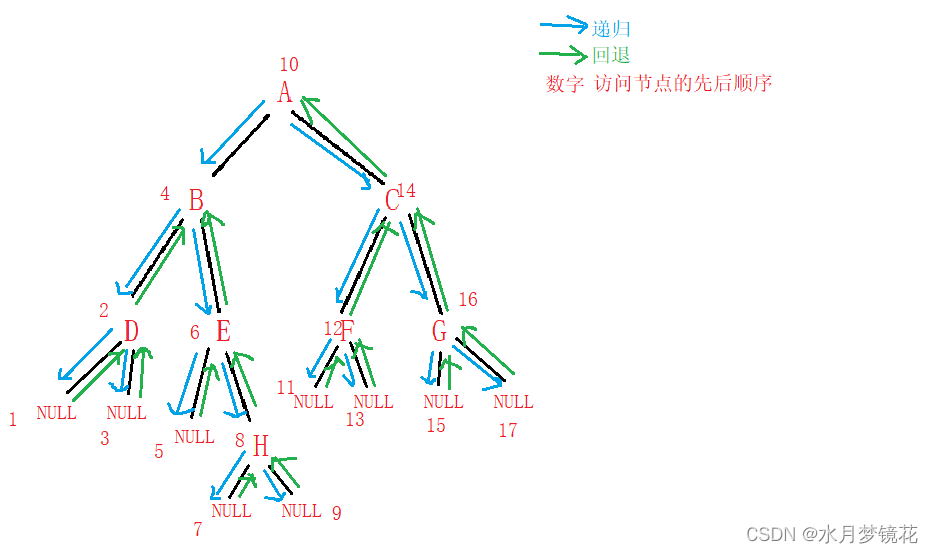
对于下面二叉树的递归展开图:
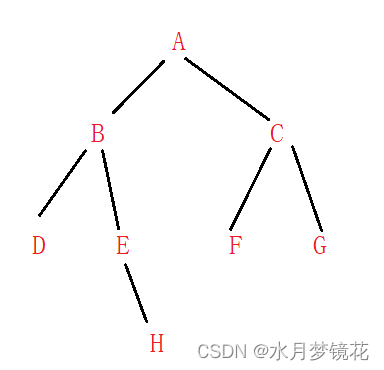

二叉树第K层节点个数(BinaryTreeLevelKSize)
函数声明:
int BinaryTreeLevelKSize(BTNode* root, int k);
子问题:根节点左子树第K-1层节点个数 与 根节点右子树第K-1层节点个数
结束条件:访问到空节点 或 找到所求层数(k == 1)
也就是说,求二叉树第K层节点数的问题转换为求根节点左子树第K-1层节点数 与 根节点右子树第K-1层节点数之和。
//二叉树第K层节点个数 左子树的第k-1层节点数 + 右子树的第k-1层节点数 不同栈帧的k互不影响
int BinaryTreeLevelKSize(BTNode* root, int k)
{//如果 k 超过数的深度if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
对于下面二叉树,求第3层节点数的递归展开图。


二叉树叶子节点个数(BinaryTreeLeafSize)
函数声明:
int BinaryTreeLeafSize(BTNode* root);
子问题:根节点左子树叶子结点 与 根节点右子树叶子结点
结束条件:访问到空节点 或 访问到叶子结点
原问题转换成根节点左子树叶子结点个数 + 根节点右子树叶子结点个数。
//二叉树叶子节点个数 左子树的叶子节点 + 右子树的叶子结点
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
对于下面二叉树,求其叶子结点的个树的递归展开图

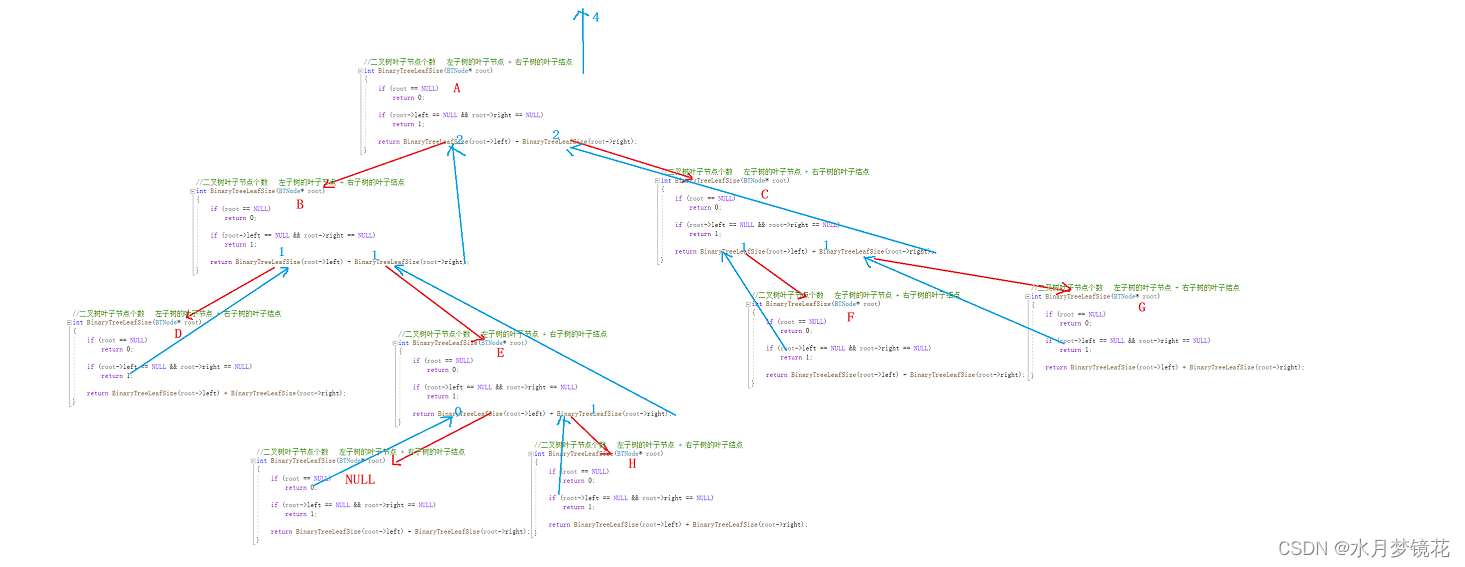
二叉树查找值为X的节点(BinaryTreeFind)
先序遍历查找节点,如果是该节点,直接返回该节点地址。如果不是该节点,继续查找该节点的左子树,如果左子树也没找到,查找右子树。
//二叉树查找值为X的节点 前序遍历查找
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* leftNode = BinaryTreeFind(root->left, x);if (leftNode != NULL)return leftNode;//右子树BTNode* rightNode = BinaryTreeFind(root->right, x);if (rightNode != NULL)return rightNode;return NULL;
}
对于下面二叉树,查找 ’ C '的递归展开图


判断二叉树是否是完全二叉树(BinaryTreeComplete)
完全二叉树也就是堆,当其层序遍历时,其中有效数据(不包含NULL)是连续的。
只需要借助队列,来层序遍历二叉树(如果某个节点左子节点或右子节点是NULL也入队列)。当队列首数据是NULL时,判断其后数据是否全是NULL,如果其后数据全是NULL,返回true,如果其后元素有一个不是NULL,返回false。
//完全二叉树的节点是连续的,层序遍历二叉树,如果遇到NULL,检查栈中后续元素是否都为NULL
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);QuenePush(&q, root);while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QuenePush(&q, node->left);QuenePush(&q, node->right);}else{break;}}while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QueneDestrory(&q);return false;}}QueneDestrory(&q);return true;
}
通过前序遍历的数组构建二叉树
在先序遍历的数组中,我们以’ # '代表NULL。
函数声明:其中a是先序遍历的数组,n是节点数,pi是现在节点的个数
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
子问题:构建左子树与右子树
结束条件:遇到先序遍历数组的’ # '或节点数大于n
创建根节点,再遍历左子树和右子树,使根节点指向左子树与右子树。
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* newnode = BuyBinaryTreeNode(a[*pi]);(*pi)++;//左子节点BTNode* leftnode = BinaryTreeCreate(a, n, pi);newnode->left = leftnode;//右子节点BTNode* rightnode = BinaryTreeCreate(a, n, pi);newnode->right = rightnode;return newnode;
}
四、代码展示
二叉树代码展示
#pragma once#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <string.h>typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);//二叉树的销毁
void BinaryTreeDestroy(BTNode* root);//二叉树节点个数
int BinaryTreeSize(BTNode* root);//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);//二叉树查找值为X的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);//二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);//二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);//二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);//层序遍历
void BinaryTreeLevelOrder(BTNode* root);//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x);
#include "BinaryTree.h"
#include "quene.h"//创建二叉树的节点
BTNode* BuyBinaryTreeNode(BTDataType x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc:");exit(-1);}root->data = x;root->left = root->right = NULL;return root;
}//二叉树前序遍历 根节点 左子树 右子树
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//根节点printf("%c ", root->data);//左子树BinaryTreePrevOrder(root->left);//右子树BinaryTreePrevOrder(root->right);
}//二叉树中序遍历 左子树 根 右子树
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreeInOrder(root->left);//根printf("%c ", root->data);//右子树BinaryTreeInOrder(root->right);
}//二叉树后序遍历 左子树 右子树 根
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}//左子树BinaryTreePostOrder(root->left);//右子树BinaryTreePostOrder(root->right);//根printf("%c ", root->data);
}//二叉树的销毁 后序遍历二叉树
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL){return;}//左子树BinaryTreeDestroy(root->left);//右子树BinaryTreeDestroy(root->right);//根free(root);
}//二叉树节点个数 根节点的左子树与右子树的节点个数和
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}// 左子树节点数 右子树节点数 根节点return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}//二叉树叶子节点个数 左子树的叶子节点 + 右子树的叶子结点
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}//二叉树第K层节点个数 左子树的第k层节点数 + 右子树的第k层节点数 不同栈帧的k互不影响
int BinaryTreeLevelKSize(BTNode* root, int k)
{//如果 k 超过数的深度if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}//二叉树查找值为X的节点 前序遍历查找
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* leftNode = BinaryTreeFind(root->left, x);if (leftNode != NULL)return leftNode;//右子树BTNode* rightNode = BinaryTreeFind(root->right, x);if (rightNode != NULL)return rightNode;return NULL;
}//层序遍历 借助队列 出队头数据时,将其左子节点 与 右子节点依次入队列
void BinaryTreeLevelOrder(BTNode* root)
{Quene q;QueneInit(&q);//入根节点QuenePush(&q, root);//队列为空,代表二叉树中元素也遍历完成while (!QueneEmpty(&q)){QDataType val = QueneFront(&q);printf("%c ", val->data);//入数据 该节点的左节点 与 右节点if (val->left != NULL)QuenePush(&q, val->left);if (val->right != NULL)QuenePush(&q, val->right);//出队头数据QuenePop(&q);}QueneDestrory(&q);
}//判断二叉树是否是完全二叉树 层序遍历二叉树//bool BinaryTreeComplete(BTNode* root)
//{
// Quene q;
// QueneInit(&q);
//
// //如果某个节点的右节点为空,那么之后遍历的节点的左/右节点也应该为空
// bool flag = false;
//
// QuenePush(&q, root);
// while (!QueneEmpty(&q))
// {
// QDataType val = QueneFront(&q);
//
// if (val->left == NULL && val->right != NULL)
// return false;
//
// if (flag == true && (val->left != NULL || val->right != NULL))
// return false;
//
// if (val->left != NULL)
// QuenePush(&q, val->left);
//
// if (val->right != NULL)
// QuenePush(&q, val->right);
// else
// flag = true;
//
// QuenePop(&q);
// }
//
// return true;
//}//完全二叉树的节点是连续的,层序遍历二叉树,如果遇到NULL,检查栈中后续元素是否都为NULL
bool BinaryTreeComplete(BTNode* root)
{Quene q;QueneInit(&q);QuenePush(&q, root);while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QuenePush(&q, node->left);QuenePush(&q, node->right);}else{break;}}while (!QueneEmpty(&q)){BTNode* node = QueneFront(&q);QuenePop(&q);if (node != NULL){QueneDestrory(&q);return false;}}QueneDestrory(&q);return true;
}//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}BTNode* newnode = BuyBinaryTreeNode(a[*pi]);(*pi)++;//左子节点BTNode* leftnode = BinaryTreeCreate(a, n, pi);newnode->left = leftnode;//右子节点BTNode* rightnode = BinaryTreeCreate(a, n, pi);newnode->right = rightnode;return newnode;
}
队列代码展示
#include "BinaryTree.h"
#include <assert.h>//队列 节点结构--树节点
typedef struct QueneNode
{struct BinaryTreeNode* data;struct QueneNode* next;
}QueneNode;typedef struct BinaryTreeNode* QDataType;//队列 结构
typedef struct Quene
{QueneNode* head;QueneNode* tail;int size;
}Quene;//初始化队列
void QueneInit(Quene* q);//队尾入队列
void QuenePush(Quene* q, QDataType x);//队头出数据
void QuenePop(Quene* q);//获取队列头部元素
QDataType QueneFront(Quene* q);//获取队列队尾元素
QDataType QueneBack(Quene* q);//获取队列中有效元素个数
int QueneSize(Quene* q);//检查队列是否为空,如果为空返回ture,如果非空返回false
bool QueneEmpty(Quene* q);//销毁队列
void QueneDestrory(Quene* q);
#include "quene.h"//初始化队列
void QueneInit(Quene* q)
{assert(q);q->head = q->tail = NULL;q->size = 0;
}//队尾入队列
void QuenePush(Quene* q, QDataType x)
{assert(q);QueneNode* newnode = (QueneNode*)malloc(sizeof(QueneNode));if (newnode == NULL){perror("malloc");exit(-1);}newnode->next = NULL;newnode->data = x;//队列为空if (QueneEmpty(q) == true){q->head = q->tail = newnode;}else//队列不为空{q->tail->next = newnode;q->tail = newnode;}q->size++;
}//队头出数据
void QuenePop(Quene* q)
{assert(q);//队列为空assert(QueneEmpty(q) != true);//队列只有一个元素if (q->head->next == NULL){free(q->head);q->head = q->tail = NULL;}else//队列中有多个元素{QueneNode* next = q->head->next;free(q->head);q->head = next;}q->size--;
}//获取队列头部元素
QDataType QueneFront(Quene* q)
{assert(q);return q->head->data;
}//获取队列队尾元素
QDataType QueneBack(Quene* q)
{assert(q);return q->tail->data;
}//获取队列中有效元素个数
int QueneSize(Quene* q)
{assert(q);return q->size;
}//检查队列是否为空,如果为空返回ture,如果非空返回false
bool QueneEmpty(Quene* q)
{assert(q);return q->size == 0;
}//销毁队列
void QueneDestrory(Quene* q)
{assert(q);QueneNode* cur = q->head;while (cur){QueneNode* next = cur->next;free(cur);cur = next;}}
总结
以上就是我对于二叉树的理解!!!

相关文章:

数据结构:二叉树的递归实现(C实现)
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》 文章目录 前言一、树的概念二、二叉树二叉树的概念二叉树的性质 三、二叉树链式结构实现二叉树节点定义创建二叉树节点遍历二叉树先序遍历二叉树(BinaryTreePrevOrder)中序遍历二叉树(BinaryTree…...

MinGW编译运行报错RTTI symbol not found for class ‘XXX‘
最近在调试程序时莫名的出现图中报错: 还遇到过for class QObject,在此记录一下,排查后发现,原因都是有资源被重复释放导致的。...
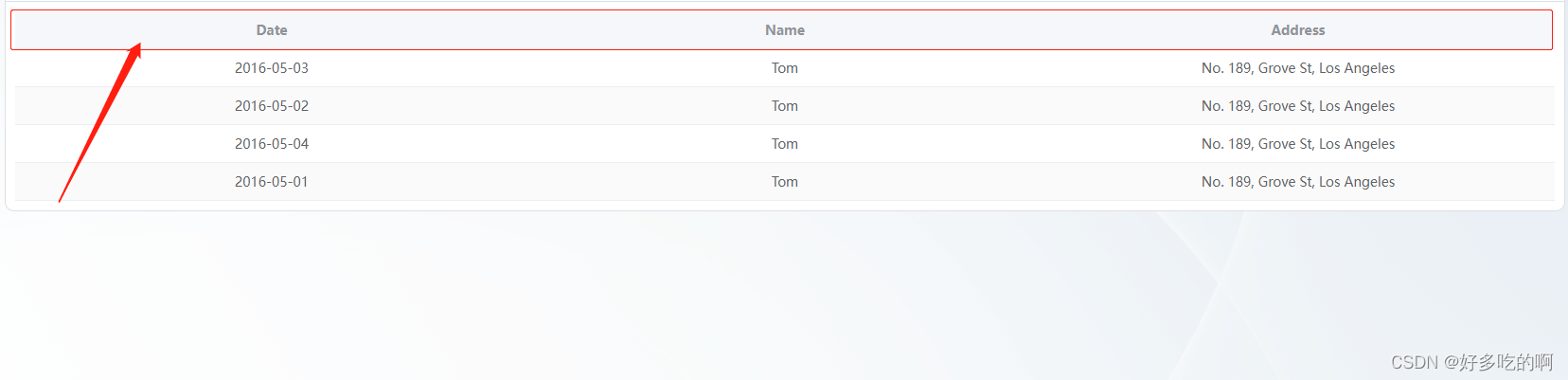
table表头颜色 element plus
原图 预期 css :deep(.el-table__header) {background-color: #F5F7FA;} :deep(.el-table tr) {background-color: rgba(0,0,0,0);} :deep(.el-table th.el-table__cell) {background-color: rgba(0,0,0,0);}...

网络安全(自学)
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全…...
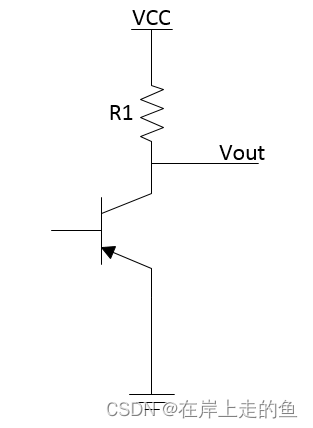
FPGA芯片IO口上下拉电阻的使用
FPGA芯片IO口上下拉电阻的使用 为什么要设置上下拉电阻一、如何设置下拉电阻二、如何设置上拉电阻为什么要设置上下拉电阻 这里以高云FPGA的GW1N-UV2QN48C6/I5来举例,这个芯片的上电默认初始化阶段,引脚是弱上来模式,且模式固定不能通过软件的配置来改变。如下图所示: 上…...

掌握指针进阶:一篇带你玩转函数指针、函数指针数组及指向函数指针数组的指针!!
🍁博客主页:江池俊的博客 💫收录专栏:C语言进阶之路 💡代码仓库:江池俊的代码仓库 🎪我的社区:GeekHub 🎉欢迎大家点赞👍评论📝收藏⭐ 文章目录 一…...

在Docker上部署2台节点,利用Keeplived实现双节点VIP 高可用,不需要关闭Keeplived,实现vip来回切换。
前言: keeplived的做高可用网上有很多例子,但是都存在这样那样的问题,比如: 1.使用的是默认抢占式,这样在主节点恢复后,又会将VIP 漂移回到主节点上,因此需要使用非抢占式模式,故障恢复时,可避免 VIP 切换造成的服务延迟。 2.使用的是默认组播,信息都会向默认的224.0.…...
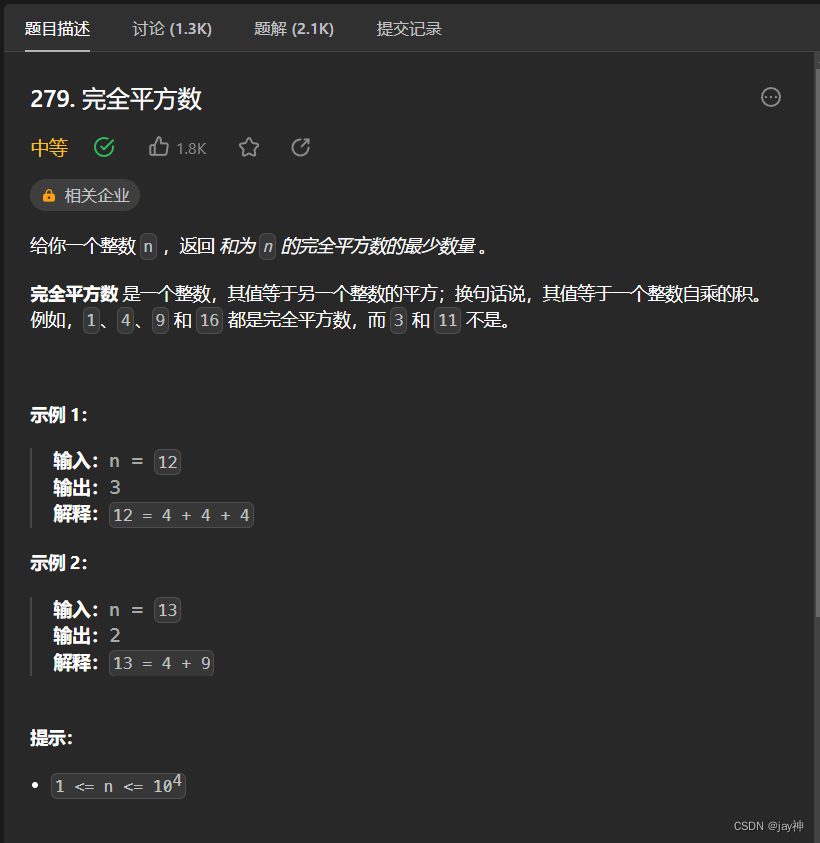
leetcode 279. 完全平方数
2023.8.18 与零钱兑换相似,本题属于完全背包问题:完全平方数为物品,整数n为背包。 直接上代码: class Solution { public:int numSquares(int n) {vector<int> dp(n1 , INT_MAX);dp[0] 0;for(int i1; i*i<n; i){for(in…...
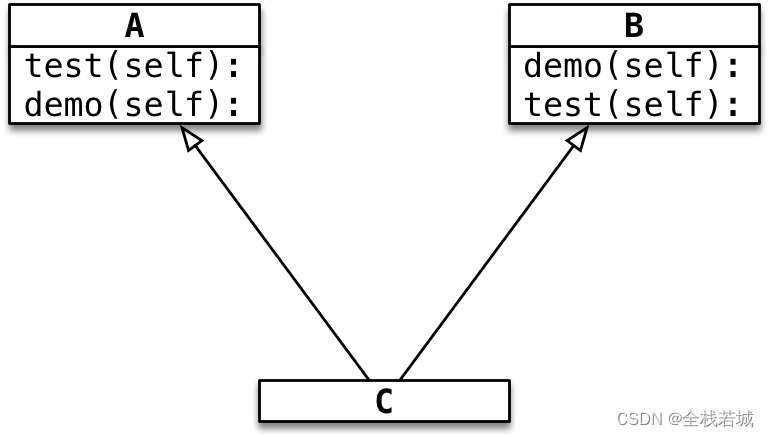
【从零学习python 】48.Python中的继承与多继承详解
文章目录 在Python中,继承可以分为单继承、多继承和多层继承。单继承 继承语法多继承 语法格式使用多继承时需要注意以下事项Python中的MRO新式类和旧式(经典)类 进阶案例 在Python中,继承可以分为单继承、多继承和多层继承。 单…...
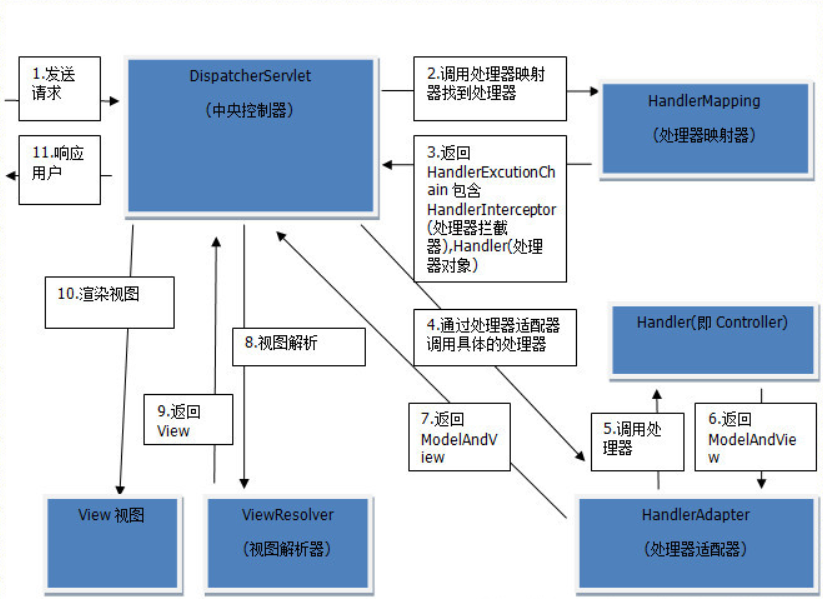
二、编写第一个 Spring MVC 程序(总结项目报 404 问题以及 Spring MVC 的执行流程)
文章目录 一、编写第一个 Spring MVC 程序二、项目运行时报 404错误原因总结三、Spring MVC 的执行流程 一、编写第一个 Spring MVC 程序 创建 maven 项目,以此项目为父项目,在父项目的 pom.xml 中导入相关依赖 <dependencies><dependency…...

okhttp源码简单流程分析
拦截器详细解析可以看大佬简书 "https://www.jianshu.com/p/6fac73f7570f"和 “https://www.jianshu.com/p/3c740829475c” okhttp请求流程 1:OkHttpClient okHttpClient new OkHttpClient.Builder() 构建一个okhttpClient对象,传入你想传入的…...
SpringBoot整合Shiro实现登录认证,鉴权授权
文章目录 前言一、shiro简介二、环境搭建2.1.数据库2.1.1user用户表2.1.2user_role用户角色关系表2.1.3role角色表2.1.4role_permission角色权限关系表2.1.5permission权限表 2.2导坐标2.3实体类2.3.1User2.3.2Role2.3.3Permission 2.4MVC三层2.4.1User2.4.1.1mapper层2.4.1.2s…...
Airbnb开源数据可视化工具Visx
一、什么是visx visx 是用于 React 的富有表现力的底层可视化组件集合,结合了 d3 的强大功能来生成可视化,以及 React 更新 DOM 的诸多优势。 在 Airbnb 内部,visx 的目标是统一整个公司的可视化堆栈,在此过程中,创建了 visx 项目,从而有效的将 D3 的强大功能与 React …...
VR仿真实训系统编辑平台赋予老师更多自由和灵活性
为了降低院校教师在VR虚拟现实方面应用的门槛,VR公司深圳华锐视点融合多年的VR虚拟仿真实训系统制作经验,制作了VR动物课件编辑器,正在逐渐受到师生们的关注和应用。 简单来说,VR畜牧专业课件编辑器是一种可以制作虚拟现实动物教学…...

父类对象转成子类对象
import org.springframework.beans.BeanUtils; import java.util.ArrayList; import java.util.List; public class Test {public static void main(String[] args) {List<B> bList new ArrayList<>();B b new B("a","这是a","b",…...

Spring Boot中如何使用Flyway进行数据库迁移
在本文中,我们将了解如何使用 Flyway 来管理 Spring Boot 应用程序中的 SQL 数据库架构。 在本文中,我们将了解如何使用 Flyway 来管理Spring Boot应用程序中的SQL 数据库架构。 Flyway是一个数据库迁移工具,它提供迁移历史和回滚的功能&…...
)
web在线编辑器(vue版)
目录 前言一、monaco-editor1、源码2、体积优化 二、ace-editor?1、源码2、体积优化 总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多…...
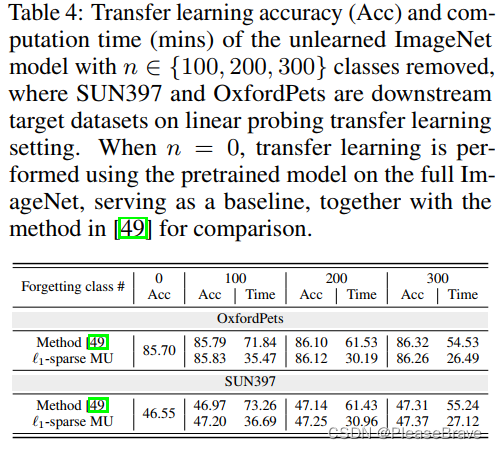
【论文阅读】 Model Sparsity Can Simplify Machine Unlearning
Model Sparsity Can Simplify Machine Unlearning 背景主要内容Contribution Ⅰ:对Machine Unlearning的一个全面的理解Contribution Ⅱ:说明model sparsity对Machine Unlearning的好处Pruning方法的选择sparse-aware的unlearning framework Experiments…...
Spring Clould 部署 - Docker
视频地址:微服务(SpringCloudRabbitMQDockerRedis搜索分布式) 初识Docker-什么是Docker(P42,P43) 微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。 分布式系统中&…...

linux--链表动态创建
头插法: 核心代码: s->next head->next; head->next s; 尾插法 核心代码: tail head; s->next NULL; tail->next s; tail s; 当用头插法依次插入值分别为1,2,3,4,5的结点后, 单链表顺序为: he…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
