Codeforces Round 893 (Div. 2)B题题解
文章目录
- [The Walkway](https://codeforces.com/contest/1858/problem/B)
- 问题建模
- 问题分析
- 1.分析所求
- 2.如何快速计算每个商贩被去除后的饼干数量
- 代码
The Walkway


问题建模
给定n个椅子,其中有m个位置存在商贩,在商贩处必须购买饼干吃,每隔经过d个椅子需要消耗饼干,在初始椅子1处也需要吃饼干,现在可以去除一个商贩,问去除一个商贩后所需消耗的饼干数量最小为多少,以及符合要求的商贩数量。
问题分析
1.分析所求
题目需要输出一个最小的饼干数量,以及对应符合要求的商贩数量。则可以考虑采用枚举计算每个商贩缺失后所需的饼干数量,取数量最小的情况即可。
2.如何快速计算每个商贩被去除后的饼干数量
由于到商贩处必须买饼干,也就是到商贩处计算椅子的间隔需要重新计算,则只需按商贩间隔计算饼干数量即可。由于只去除一个商贩,则可以预处理出所有商贩都存在的饼干数量,然后计算出去除商贩所需饼干数最少的情况即可。
代码
#include<bits/stdc++.h>#define x first
#define y second
#define C(i) str[0][i]!=str[1][i]
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N = 1e5+10, INF = 0x3f3f3f3f;
int s[N];void solve() {int n,m,d;cin >>n >>m >>d;for(int i=1;i<=m;i++) cin >>s[i];///计算方便计算第一个椅子和最后一个椅子到商贩的间隔s[0]=1-d,s[m+1]=n+1;int ans=m;for(int i=0;i<=m;i++) ans+=(s[i+1]-s[i]-1)/d;int val=0,cnt=0;///计算去除商贩后减少饼干数量最多的for(int i=1;i<=m;i++){int a=s[i]-s[i-1]-1;int b=s[i+1]-s[i]-1;int c=s[i+1]-s[i-1]-1;if(val<a/d+b/d-c/d+1) val=a/d+b/d-c/d+1,cnt=1;else if(val==a/d+b/d-c/d+1) cnt++;}cout <<ans-val <<" " <<cnt<<'\n';
}int main() {int t = 1;cin >> t;while (t--) solve();return 0;
}
相关文章:

Codeforces Round 893 (Div. 2)B题题解
文章目录 [The Walkway](https://codeforces.com/contest/1858/problem/B)问题建模问题分析1.分析所求2.如何快速计算每个商贩被去除后的饼干数量代码 The Walkway 问题建模 给定n个椅子,其中有m个位置存在商贩,在商贩处必须购买饼干吃,每隔…...
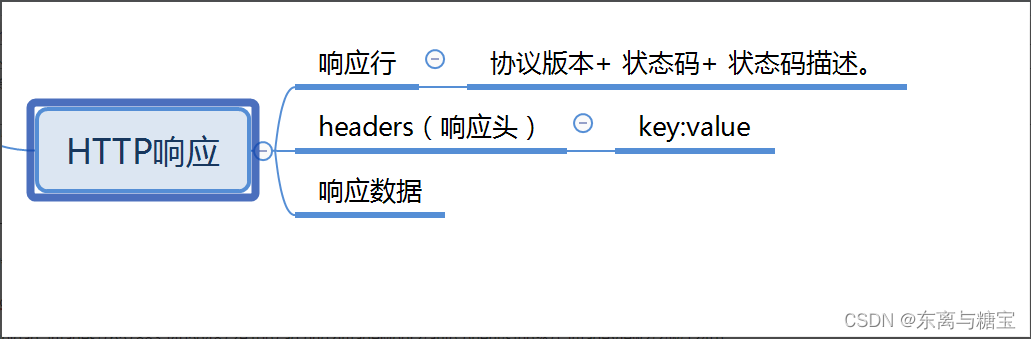
HTTP响应状态码大全:从100到511,全面解析HTTP请求的各种情况
文章目录 前言一、认识响应状态码1. 什么是HTTP响应状态码2. Http响应状态码的作用3. 优化和调试HTTP请求的建议 二、1xx 信息响应1. 认识http信息响应2. 常见的信息响应状态码 三、2xx 成功响应1. 认识HTTP成功响应2. 常见的成功响应状态码 四、3xx 重定向1. 认识http重定向2.…...

Vue-10.集成.env
.env、.env.development 和 .env.preview .env、.env.development 和 .env.preview 文件是用于配置环境变量和应用程序设置的文件,它们在项目开发和部署过程中起到关键作用。这些文件用于在不同的环境中设置不同的变量值,以满足不同环境下的配置需求。 …...

强训第33天
选择 C A ping是TCP/IP协议族的一部分,使用ICMP协议,ICMP底层使用IP协议。如果要ping其他网段,则需要设置网关。 如果是二层交换机故障,则ping同网段的也会不通。 C Dos攻击被称之为“拒绝服务攻击”,其目的是使计算机…...
【CTF-web】buuctf-[极客大挑战 2019]EasySQL 1(sql注入)
题目链接 根据题目判断出可能需要sql注入,看源码可知数据是通过GET的方式传输的,即放在url的username和password两个参数中。 只要将username输入为1 or 11#,password可以为任何值,即可顺利登录。 需要注意的是url中的井号表示…...

脚本语言与编译语言的区别
文章目录 一、语法差异二、执行方式差异三、应用领域差异四、总结 一、语法差异 脚本语言:脚本语言通常使用解释器逐行执行,不需要事先编译。它的语法相对简单,易于学习和使用。常见的脚本语言有Python、JavaScript和Ruby等。 编译语言&…...

大型企业或者组织,组建专属的虚拟局域网,深入理解相关的配置和搭建使用、网络加速和网络优化,可夸地区夸国际使用,深入搞懂每项配置的作用和含义
大型企业或者组织,组建专属的虚拟局域网,深入理解相关的配置和搭建使用、网络加速和网络优化,可夸地区夸国际使用,深入搞懂每项配置的作用和含义。 1、openxxx介绍与图解 1.1 openxxx介绍 openxxx 是一个基于 OpenSSL库的应用层 虚拟局域网 实现。和传统 虚拟局域网 相…...

数据结构:二叉树的递归实现(C实现)
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》 文章目录 前言一、树的概念二、二叉树二叉树的概念二叉树的性质 三、二叉树链式结构实现二叉树节点定义创建二叉树节点遍历二叉树先序遍历二叉树(BinaryTreePrevOrder)中序遍历二叉树(BinaryTree…...

MinGW编译运行报错RTTI symbol not found for class ‘XXX‘
最近在调试程序时莫名的出现图中报错: 还遇到过for class QObject,在此记录一下,排查后发现,原因都是有资源被重复释放导致的。...
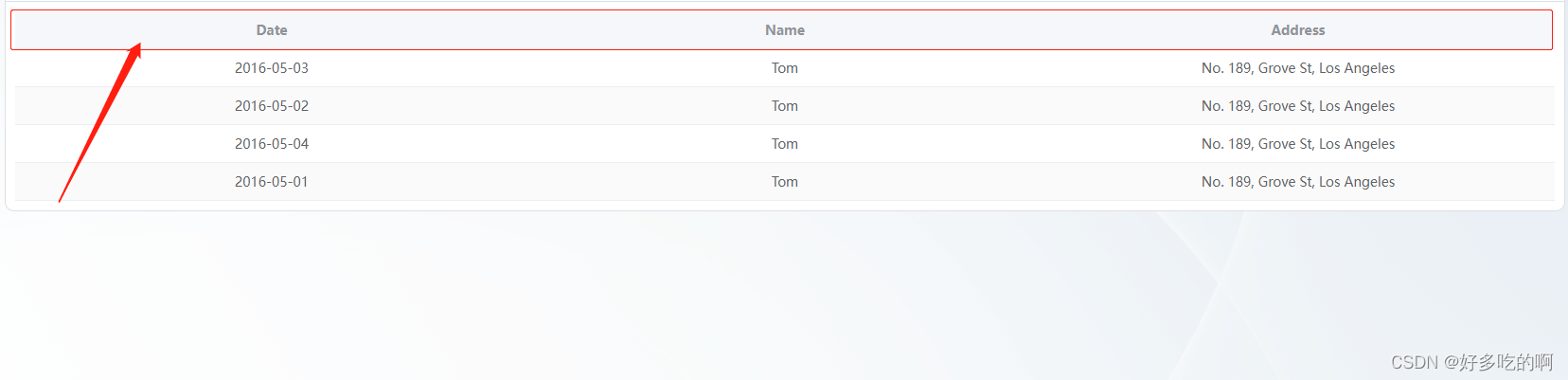
table表头颜色 element plus
原图 预期 css :deep(.el-table__header) {background-color: #F5F7FA;} :deep(.el-table tr) {background-color: rgba(0,0,0,0);} :deep(.el-table th.el-table__cell) {background-color: rgba(0,0,0,0);}...

网络安全(自学)
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全…...
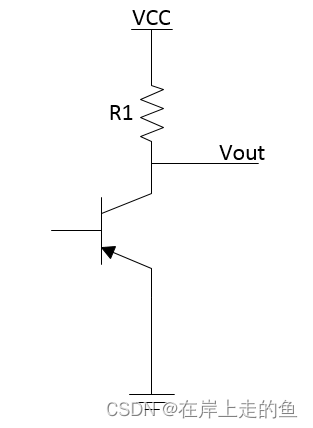
FPGA芯片IO口上下拉电阻的使用
FPGA芯片IO口上下拉电阻的使用 为什么要设置上下拉电阻一、如何设置下拉电阻二、如何设置上拉电阻为什么要设置上下拉电阻 这里以高云FPGA的GW1N-UV2QN48C6/I5来举例,这个芯片的上电默认初始化阶段,引脚是弱上来模式,且模式固定不能通过软件的配置来改变。如下图所示: 上…...

掌握指针进阶:一篇带你玩转函数指针、函数指针数组及指向函数指针数组的指针!!
🍁博客主页:江池俊的博客 💫收录专栏:C语言进阶之路 💡代码仓库:江池俊的代码仓库 🎪我的社区:GeekHub 🎉欢迎大家点赞👍评论📝收藏⭐ 文章目录 一…...

在Docker上部署2台节点,利用Keeplived实现双节点VIP 高可用,不需要关闭Keeplived,实现vip来回切换。
前言: keeplived的做高可用网上有很多例子,但是都存在这样那样的问题,比如: 1.使用的是默认抢占式,这样在主节点恢复后,又会将VIP 漂移回到主节点上,因此需要使用非抢占式模式,故障恢复时,可避免 VIP 切换造成的服务延迟。 2.使用的是默认组播,信息都会向默认的224.0.…...
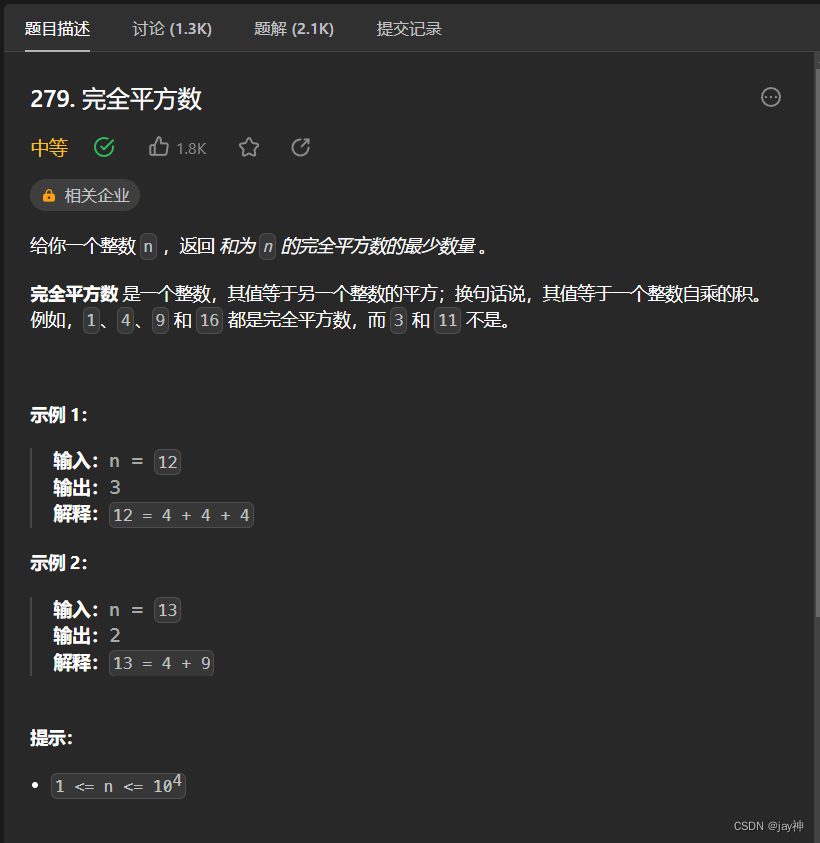
leetcode 279. 完全平方数
2023.8.18 与零钱兑换相似,本题属于完全背包问题:完全平方数为物品,整数n为背包。 直接上代码: class Solution { public:int numSquares(int n) {vector<int> dp(n1 , INT_MAX);dp[0] 0;for(int i1; i*i<n; i){for(in…...
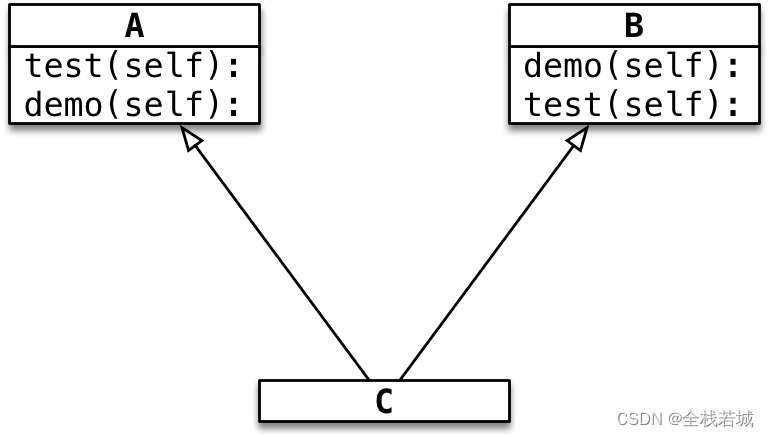
【从零学习python 】48.Python中的继承与多继承详解
文章目录 在Python中,继承可以分为单继承、多继承和多层继承。单继承 继承语法多继承 语法格式使用多继承时需要注意以下事项Python中的MRO新式类和旧式(经典)类 进阶案例 在Python中,继承可以分为单继承、多继承和多层继承。 单…...
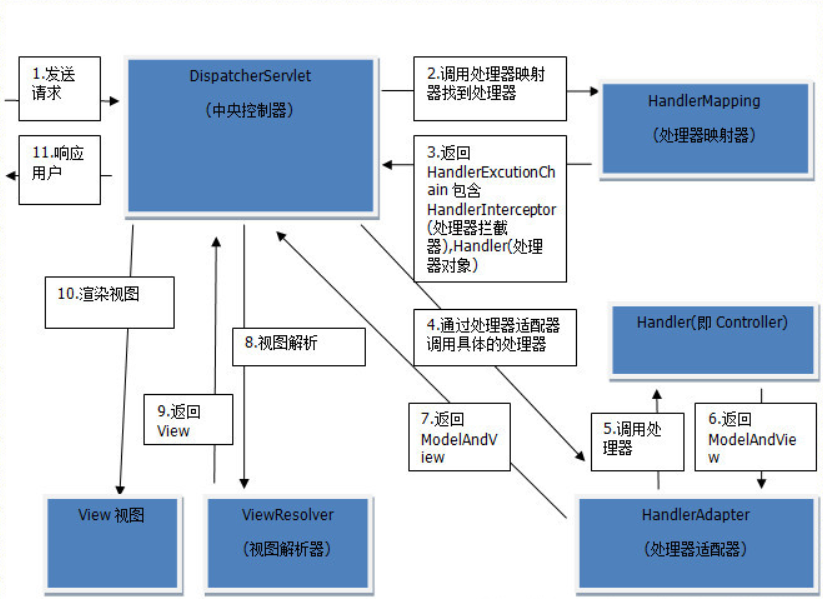
二、编写第一个 Spring MVC 程序(总结项目报 404 问题以及 Spring MVC 的执行流程)
文章目录 一、编写第一个 Spring MVC 程序二、项目运行时报 404错误原因总结三、Spring MVC 的执行流程 一、编写第一个 Spring MVC 程序 创建 maven 项目,以此项目为父项目,在父项目的 pom.xml 中导入相关依赖 <dependencies><dependency…...

okhttp源码简单流程分析
拦截器详细解析可以看大佬简书 "https://www.jianshu.com/p/6fac73f7570f"和 “https://www.jianshu.com/p/3c740829475c” okhttp请求流程 1:OkHttpClient okHttpClient new OkHttpClient.Builder() 构建一个okhttpClient对象,传入你想传入的…...
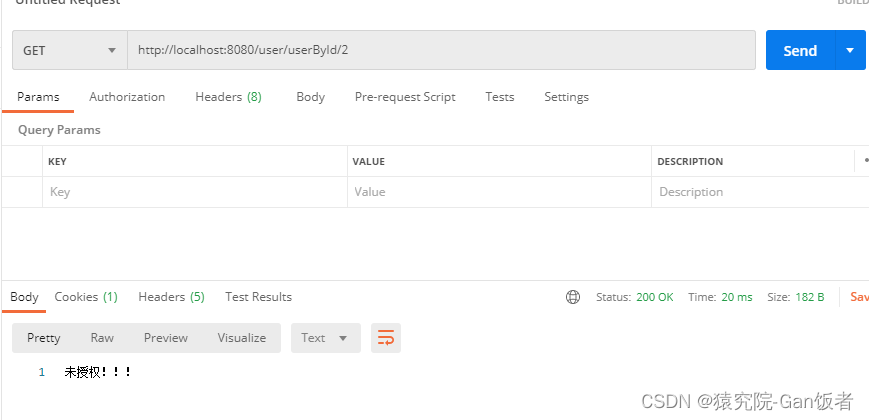
SpringBoot整合Shiro实现登录认证,鉴权授权
文章目录 前言一、shiro简介二、环境搭建2.1.数据库2.1.1user用户表2.1.2user_role用户角色关系表2.1.3role角色表2.1.4role_permission角色权限关系表2.1.5permission权限表 2.2导坐标2.3实体类2.3.1User2.3.2Role2.3.3Permission 2.4MVC三层2.4.1User2.4.1.1mapper层2.4.1.2s…...
Airbnb开源数据可视化工具Visx
一、什么是visx visx 是用于 React 的富有表现力的底层可视化组件集合,结合了 d3 的强大功能来生成可视化,以及 React 更新 DOM 的诸多优势。 在 Airbnb 内部,visx 的目标是统一整个公司的可视化堆栈,在此过程中,创建了 visx 项目,从而有效的将 D3 的强大功能与 React …...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
