信息与通信工程面试准备——数学知识|正态分布|中心极限定理
目录
正态分布
正态分布的参数
正态分布的第一个参数是均值
正态分布的第二个参数是标准差SD
所有正态分布的共同特征
标准正态分布:正态分布的特例
中心极限定理
理解定义
示例# 1
示例# 2
知道样本均值总是正态分布的实际含义是什么?
正态分布
正态分布也被称为高斯分布或钟形曲线(因为它看起来像一个钟),这是统计学中最重要的概率分布,就像我们在大自然中经常看到的那样,它有点神奇。例如,身高、体重、血压、测量误差、智商得分等都服从正态分布。
还有一个跟它相关的,并且非常重要的概念,叫中心极限定理,我们后面会提到。

由上图可得一个正常变量的值是如何分布的。这是一个对称分布,其中大多数观测值聚集在具有最高发生概率的中心峰(均值/平均值)附近,并且当我们在两个方向上都偏离中心峰时,我们看到曲线尾部出现值的可能性越来越小。此图描绘了一个群体的智商水平,可以理解,智商水平非常低或智商水平很高的人很少见,并且大多数人都处于平均智商得分范围内。
正态分布的参数
正态分布总是以平均值为中心,而曲线的宽度则由标准差(SD)决定。

这是两个正态分布,x轴上的高度单位是英寸,y轴上是特定高度对应的人数。
1. 婴儿的平均身高为20英寸(50cm),标准差为0.6英寸(1.5cm)
2. 成年人的平均分布为70英寸(175cm),标准差为4英寸(10cm)
了解正态分布标准差的意义在于,它遵循一个经验法则,即大约95%的测量值落在均值附近的+/- 2倍个标准差之间。
推论:95%的人口落在平均值+/- 2*SD之间
1. 95%的婴儿身高在20 +/- 1.2英寸之间
2. 95%的成年人身高测量值在70 +/- 8英寸之间
正态分布的第一个参数是均值
均值或平均值是正态分布的集中趋势,它决定了曲线峰值的位置。平均值的变化导致曲线沿x轴水平移动。
正态分布的第二个参数是标准差SD
标准差是正态分布变异性的量度,它决定了曲线的宽度。SD值的变化导致曲线变得更窄或更宽,并对曲线的高度产生反比例的影响。
更紧的曲线(较小的宽度)->更高的高度
更宽的曲线(更高的宽度)->更短的高度
现在,你已经了解了正态分布曲线的所有基础知识。让我们继续学习与之相关的其他重要信息。

所有正态分布的共同特征
1. 它们都是对称的
2. 平均值=中位数
3. 根据经验法则,我们可以确定正态分布曲线离均值标准差范围内的数据百分比。
通过一个示例,这一点将变得更加清楚。

让我们来看一个披萨外卖的例子。假设一家披萨餐厅的平均配送时间为30分钟,标准偏差为5分钟。根据经验法则,我们可以确定68%的交付时间在25-35分钟(30 +/- 5)之间,95%在20-40分钟(30 +/- 2*5)之间,99.7%在15-45分钟(30 +/-3*5)之间。
标准正态分布:正态分布的特例
如前所述,正态分布根据参数值(平均值和标准差)有许多不同的形状。标准正态分布是正态分布的一个特例,均值为0,标准差为1。这个分布也称为Z分布。标准正态分布上的值称为标准分数或Z分数。标准分数表示某一特定观测值高于或低于平均值的SD数。
例如,标准得分为1.5表示观察到的结果比平均值高1.5个标准差。另一方面,负分数表示低于平均值的值。平均值的Z分数为0。
中心极限定理

中心极限定理(CLT)指出,如果样本量足够大,则变量均值的采样分布将近似于正态分布,而与该变量在总体中的分布无关。
理解定义
示例# 1

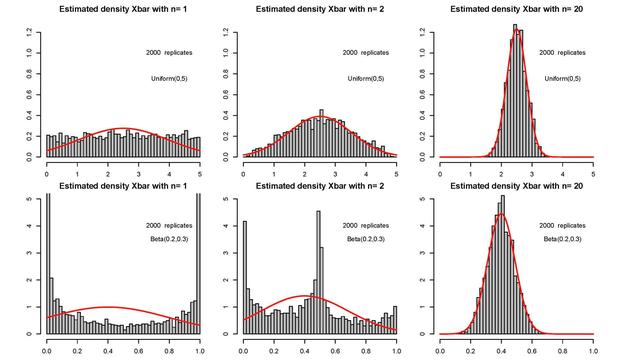
选取一个均匀分布[0,1],它被称为均匀分布,因为在0和1之间选择值的概率相等,因此它的概率密度函数(PDF)是水平的直线。现在,让我们假设我们从这个分布中随机抽取20个样本(绿点)并计算这些样本的均值,我们得到一个值,在这个例子中是0.5,用虚线表示。让我们把这个平均值画在直方图上。由于这个柱状图到目前为止只有一个平均值,它并没有告诉我们任何其他信息(左图)。继续从相同的分布中提取更多的随机样本,计算各自的平均值并将这些平均值绘制在直方图上,我们开始得到一个有趣的结果。
随着我们从均匀分布中抽取越来越多的随机样本,并在直方图上绘制样本均值,我们得到一个正态分布结果如下(见右曲线)。

推论:我们从均匀的数据分布开始,但是从中抽取的样本均值是正态分布。
示例# 2
在第二个例子中,让我们按照与第一个例子相同的步骤,唯一的不同是我们这次要从指数分布中提取样本。

我们将再次随机抽取20个样本,计算样本的均值,并将其绘制在直方图上。计算100这样的样本的均值并将其画在直方图上,这样的分布对我们来说并不陌生。样本均值是正态分布!

推论:我们从指数数据分布开始,但从中抽取样本的均值得到正态分布。
我们从指数数据分布开始,但是从中抽取的样本均值得到正态分布。因此,它在这一点上变得非常直观,中心极限定理意味着什么?
中心极限定理意味着即使数据分布不是正态的,从中抽取的样本均值的分布也是正态的。
知道样本均值总是正态分布的实际含义是什么?
在分析领域,我们每天都会遇到各种各样的数据,而源数据的分布并不总是被我们所知道的,但是,因为我们了解中心极限定理,所以我们甚至不需要关心源数据的分布,因为我们总是可以得到正态分布。
为了使中心极限定理能够起作用,我们必须能够计算出样本的平均值。有一个分布称为柯西分布,没有样本均值,从而中心极限定理论并不适用于它,但除了柯西分布,我没有遇到除中心极限定理以外的任何其他分布。)
下面是了解均值正态分布的实际含义:
1. 我们可以用均值的正态分布来分配置信区间。
2. 我们可以进行T检验(即两个样本均值之间是否存在差异)
3. 我们可以进行方差分析(即3个或更多样本的均值之间是否存在差异)
相关文章:

信息与通信工程面试准备——数学知识|正态分布|中心极限定理
目录 正态分布 正态分布的参数 正态分布的第一个参数是均值 正态分布的第二个参数是标准差SD 所有正态分布的共同特征 标准正态分布:正态分布的特例 中心极限定理 理解定义 示例# 1 示例# 2 知道样本均值总是正态分布的实际含义是什么? 正态分…...

Mybatis多表查询与动态SQL的使用
目录 1. Mybatis多表查询 1.1 添加文章表实体类 1.2 文章Interface 1.3 文章.xml 1.4 lombok的toString()有关对象打印的说明 1.5 场景: 一个用户查询多篇文章 2. 复杂情况: 动态SQL的使用 2.1 为什么要使用动态SQL? 2.2 <if>标签 2.3 <trim>标签 2.4 <where&g…...

url 和 uri 有什么区别?
URL(Uniform Resource Locator)和URI(Uniform Resource Identifier)是两个与网络资源定位和标识相关的概念,它们有一些区别,但也存在一些重叠。 URI(Uniform Resource Identifier)是…...
HCIP VLAN实验
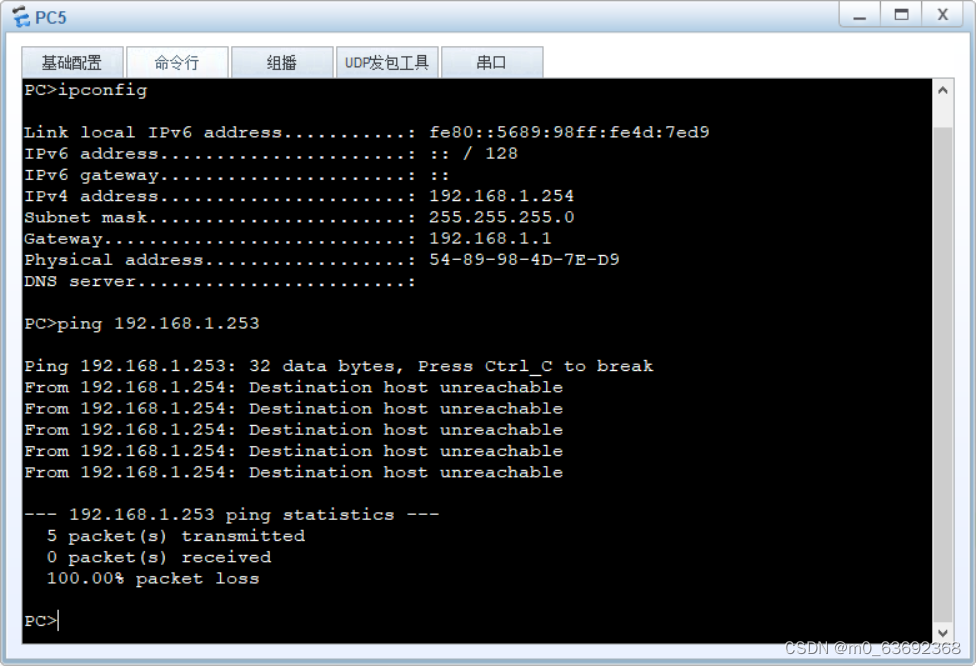
VLAN实验 拓扑图配置和分析分析配置LSW1LSW2R1 测试dhcp获取ipICMP测试 拓扑图 配置和分析 分析 从题目来看,因为 pc 1 3都是vlan2而且还是不同网段,pc 2 4 5 6在同一网段,所以可以将pc 1 2 5 4 6分在一个网段 pc4不通5 6 ,那就…...

无涯教程-Perl - waitpid函数
描述 该函数等待ID为PID的子进程终止,返回已故进程的进程ID。如果PID不存在,则返回-1。进程的退出状态包含在$?中。 可以将标志设置为各种值,这些值等于waitpid()UNIX系统调用使用的值。 FLAGS的值为0应该在支持进程的所有操作系统上工作。 语法 以下是此函数的简单语法- …...
Redis之缓存雪崩、缓存击穿、缓存穿透问题
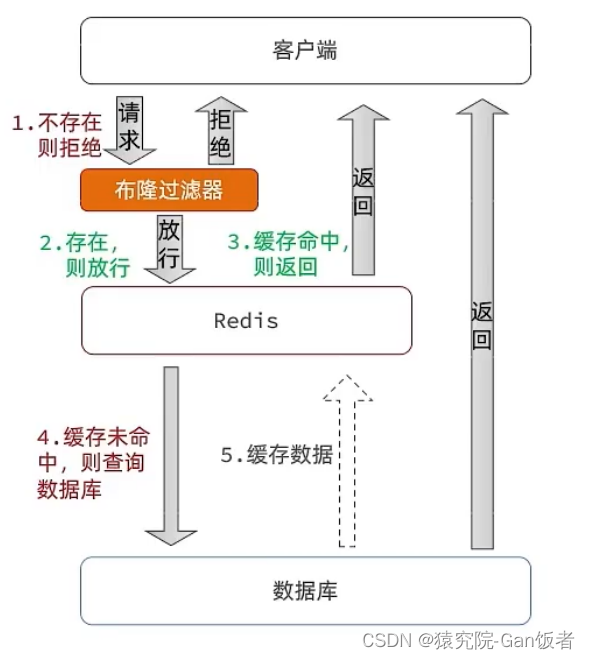
文章目录 前言一、缓存雪崩1.1、原因分析2.2、常用解决方案 二、缓存击穿2.1、原因分析2.2、常用解决方案2.2.1、使用互斥锁2.2.2、逻辑过期方案2.3、方案对比 三、缓存穿透3.1、原因分析3.2、解决方案3.2.1、缓存空对象3.2.3、布隆过滤3.3、方案对比 总结 前言 本文谈谈Redis…...
九五从零开始的运维之路(其三十五)
文章目录 前言一、概述1.概念2.组成3.特点4.工作原理5.优点: 二、各节点及其ip地址三、构建MHA1.ssh免密登录2.构建mysql主从复制(一)安装mariadb数据库并启动(二)master服务器(三)slave服务器&…...
5G科技防汛,助力守护一方平安
“立秋虽已至,炎夏尚还在”,受台风席卷以及季节性影响全国多地正面临强降水的严峻挑战。“落雨又顺秋,绵绵雨不休”,正值“七下八上” 防汛关键时期,贵州省水文水资源局已全面进入备战状态。 为确保及时响应做好防汛抢…...
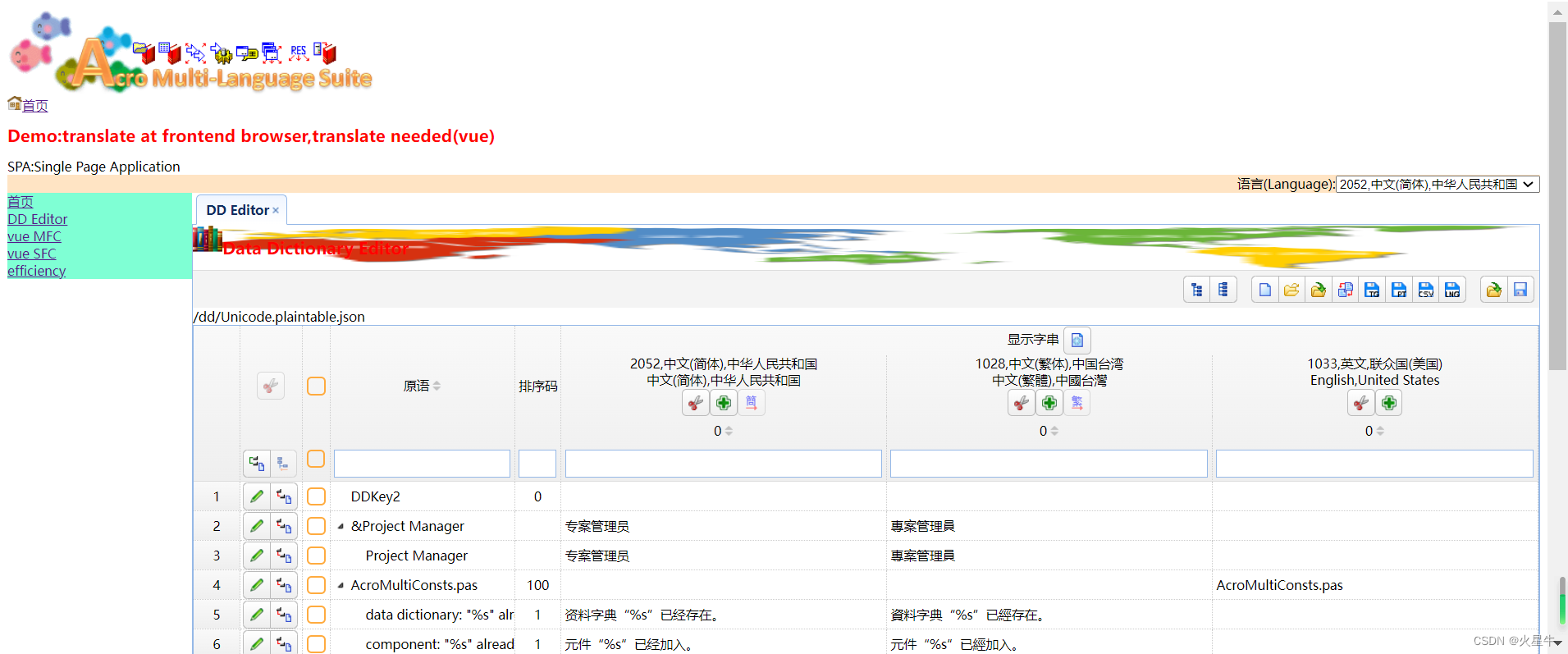
用easyui DataGrid编辑树形资料
easyui显示编辑树形资料有TreeGrid元件,但是这个元件的vue版本和react版本没有分页功能。virtual scroll功能也表现不佳。 我用DataGrid来处理。要解决的问题点: (1)如何显示成树形。即,子节点如何有缩进。 先计算好…...
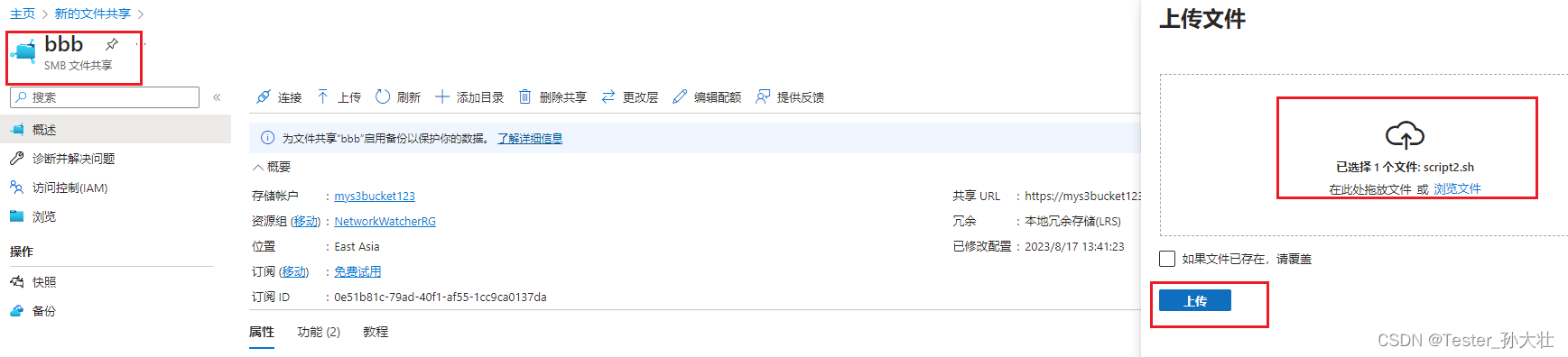
Azure存储账户
存储账户的概念 Azure存储账户是Azure提供的一种云存储解决方案,用于存储和访问各种类型的数据,包括文件、磁盘、队列、表格和Blob(二进制大对象)数据。存储账户可以基于访问模式和冗余需求来选择不同的类型,以满足应…...
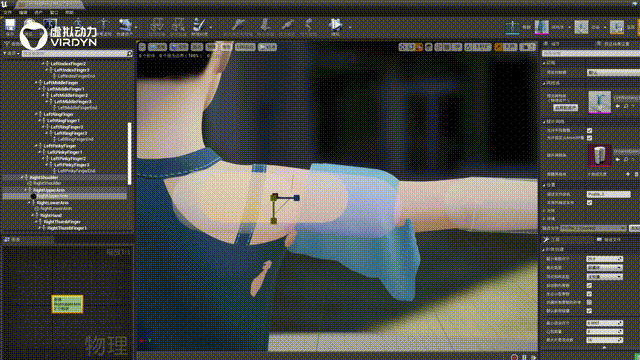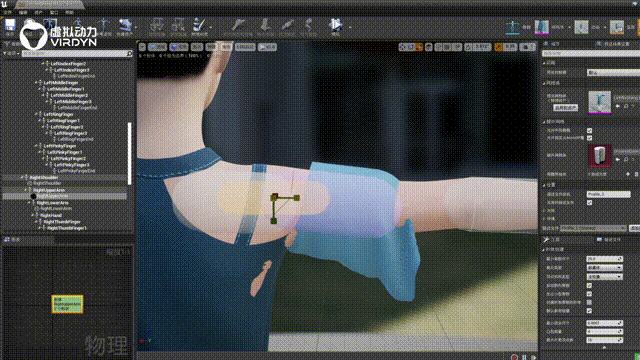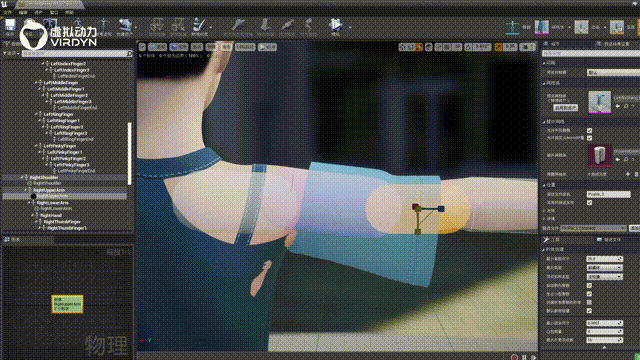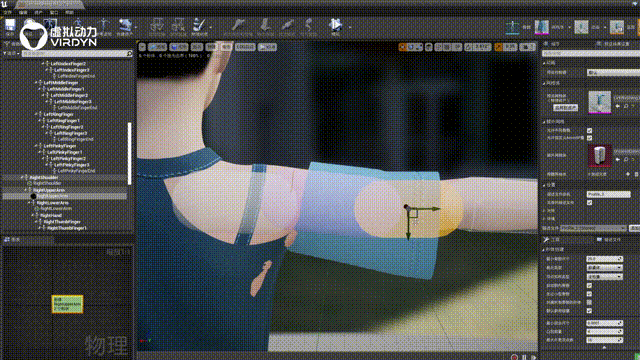
数字人服装布料解算技术服务,让数字人驱动更真实
一个数字人通过三维建模、骨骼绑定、表情绑定后,对于数字人有两种使用场景,可以使用动捕设备实时驱动,将静态的3D模型结合动捕设备实时“活”起来。数字人通过动捕设备实时驱动的过程,则是基于实时布料毛发解算方案进行技术处理的…...
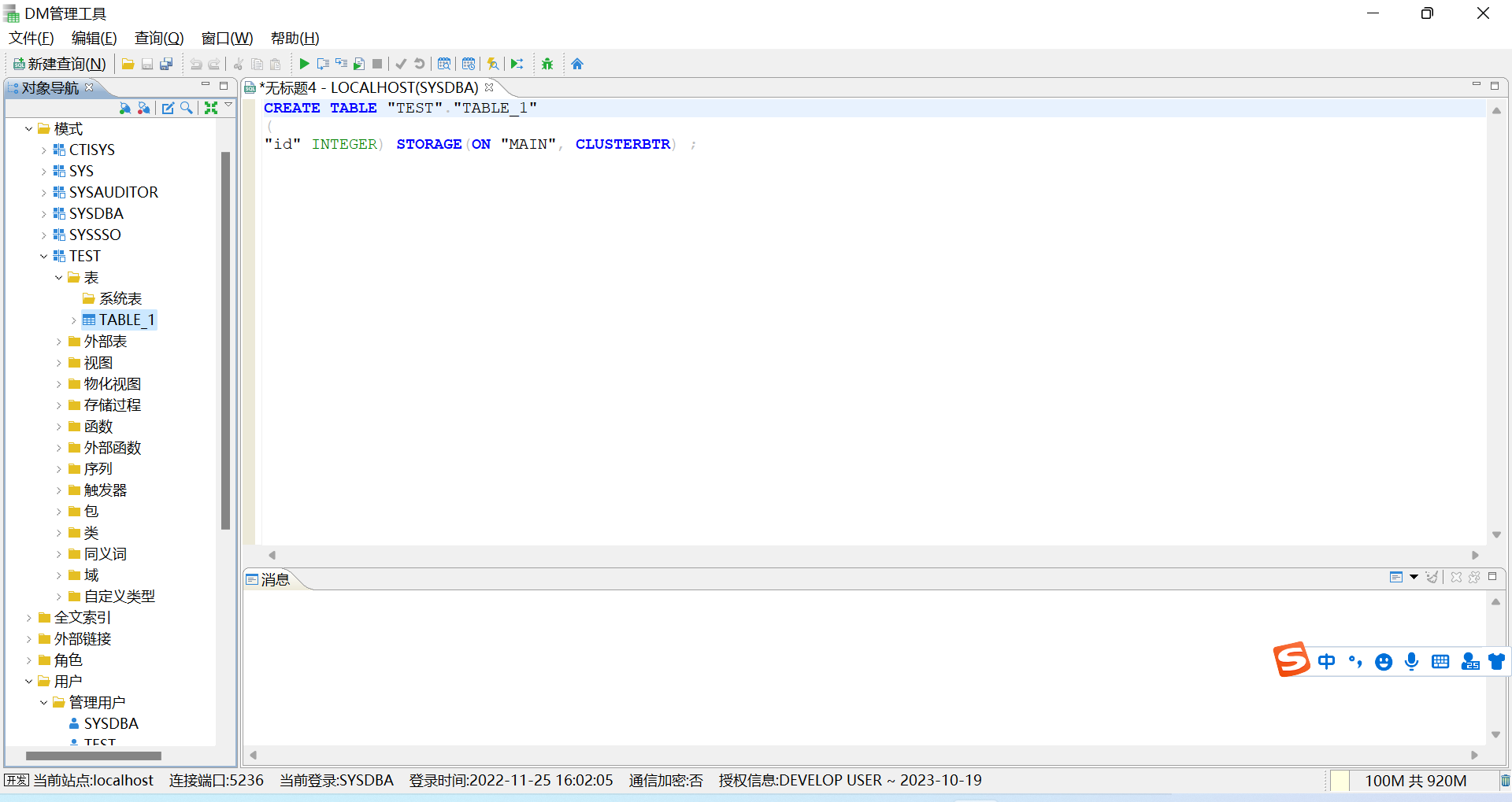
达梦数据库安装与初始化超详细教程
陈老老老板🦸 👨💻本文专栏:国产数据库-达梦数据库(主要讲一些达梦数据库相关的内容) 👨💻本文简述:本文讲一下达梦数据库的下载与安装教程(Windows版&am…...

vue输入框只能输入数字类型,禁止输入和粘贴e
js怎么去除1e里面e 方法一:使用 Number() 函数将科学计数法表示的字符串转换为数字。然后,使用 toString() 方法将其转换回字符串形式,这样就会自动移除科学计数法中的 "e" var num 1e10; // 科学计数法表示的数字 var numStr …...
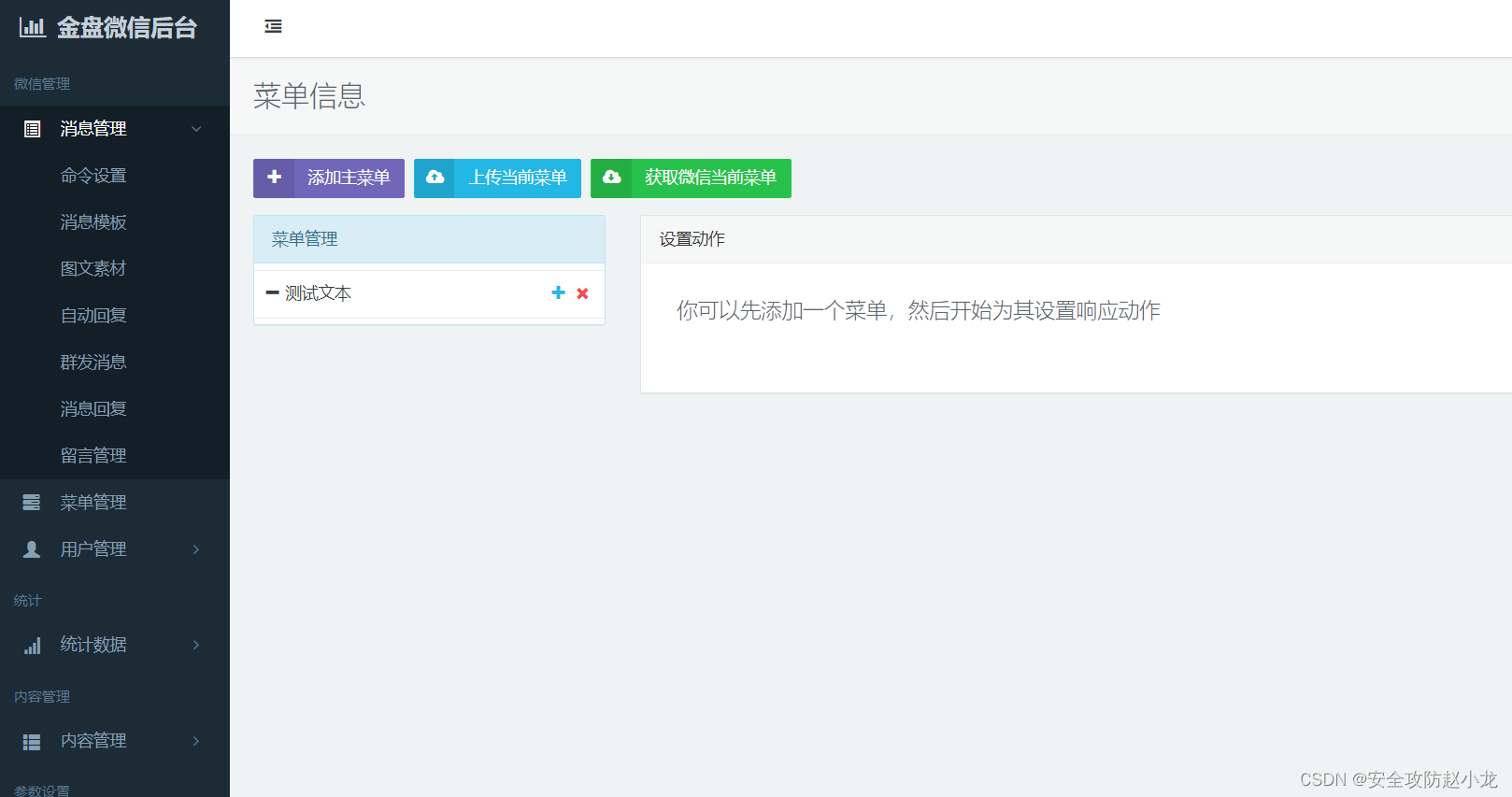
金盘 微信管理平台 getsysteminfo 未授权访问漏洞[2023-HW]
金盘 微信管理平台 getsysteminfo 未授权访问漏洞 一、漏洞描述二、漏洞影响三、网络测绘四、漏洞复现小龙POC检测: 五、 修复建议 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后…...

02-前端基础第二天-HTML5
01-HTML标签(下)导读 目标: 能够书写表格能够写出无序列表能够写出3~4个常用input表单类型能够写出下拉列表表单能够使用表单元素实现注册页面能够独立查阅W3C文档 目录: 表格标签列表标签表单标签综合案例查阅文档 02-表格标…...
i18n 配置vue项目中英文语言包(中英文转化)
一、实现效果 二、下载插件创建文件夹 2.1 下载cookie来存储 npm install --save js-cookienpm i vue-i18n -S 2.2 封装组件多页面应用 2.3 创建配置语言包字段 三、示例代码 3.1 main.js 引用 i18n.js import i18n from ./lang// 实现语言切换:i18n处理element,…...

NFTScan NFT API 在 DID Protocol 开发中的应用
自互联网发展以来,Web2.0 时代产生了网络社会,社会已经不再局限于地理边界,而 Web 3.0 引入了去中心化的理念,强调个体数据隐私和可信互操作性。在这个新的时代中,去中心化身份(Decentralized Identifier 即…...
)
内存管理(1)
内存管理(1) 1、各类型数据在内存中的存储空间2、C内存管理方式2.1 针对于内置类型分析2.2 针对于自定义类型分析2.3 C语言与C在申请动态内存失败时的区别 3、operator new 和 operator delete函数(重点)3.1 底层知识解析3.2 实现…...
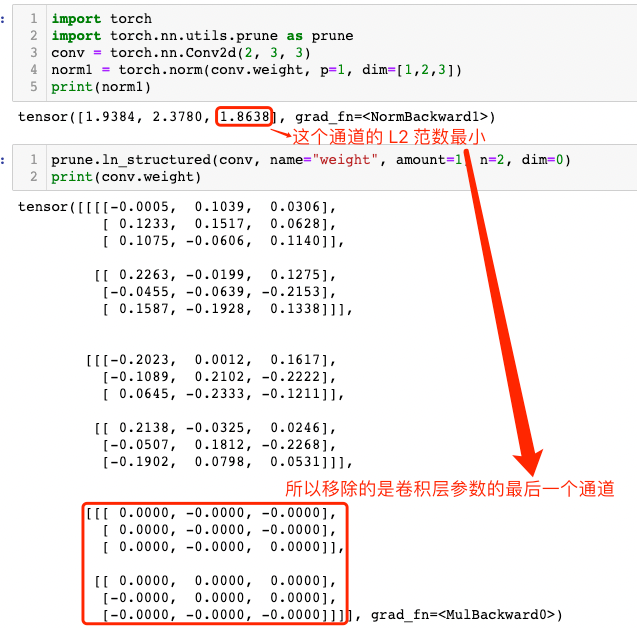
实践教程|基于 pytorch 实现模型剪枝
PyTorch剪枝方法详解,附详细代码。 一,剪枝分类 1.1,非结构化剪枝 1.2,结构化剪枝 1.3,本地与全局修剪 二,PyTorch 的剪枝 2.1,pytorch 剪枝工作原理 2.2,局部剪枝 2.3&#…...
[Docker精进篇] Docker镜像构建和实践 (三)
前言: Docker镜像构建的作用是将应用程序及其依赖打包到一个可移植、自包含的镜像中,以便在不同环境中快速、可靠地部署和运行应用程序。 文章目录 Docker镜像构建1️⃣是什么?2️⃣为什么?3️⃣镜像构建一、用现有容器构建新镜像…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
