一万字关于java数据结构堆的讲解,让你从入门到精通

目录
java类和接口总览
队列(Queue)
1. 概念
2. 队列的使用
以下是一些常用的队列操作:
1.入队操作
2.出队操作
3.判断队列是否为空
4.获取队列大小
5.其它
优先级队列(堆)
1. 优先级队列概念
Java中的PriorityQueue具有以下特点
2.常用的PriorityQueue操作
1.PriorityQueue的创建
2.插入元素
3.删除具有最高优先级的元素
4.查找具有最高优先级的元素
5.其它
3. 优先级队列的模拟实现
堆
1.堆的概念
2.堆的性质
3.堆的存储方式
4.堆的创建
1.如何把给定的一棵二叉树,变成最小堆或者最大堆
以变成最大堆为例
2.时间复杂度分析
建堆的时间复杂度
5.堆的删除
6.用堆模拟实现优先级队列
7.常用接口介绍
1.关于PriorityQueue的使用注意事项
1. 优先级队列的构造
2. 插入/删除/获取优先级最高的元素
完结撒花✿✿ヽ(°▽°)ノ✿
java类和接口总览

队列(Queue)
1. 概念
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First
In First Out) 入队列:进行插入操作的一端称为队尾(Tail/Rear) 出队列:进行删除操作的一端称为队头(Head/Front)

2. 队列的使用
在Java中,Queue是个接口,底层是通过链表实现的

Java中提供了多种队列(Queue)的实现,如LinkedList、ArrayDeque、PriorityQueue等,可以根据不同的需求选择适合的实现类。
以下是一些常用的队列操作:
1.入队操作
入队操作:使用add()或offer()方法将元素添加到队列的末尾。add()方法如果添加失败会抛出异常,而offer()方法则会返回一个boolean值表示添加是否成功。
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
queue.offer(2);2.出队操作
出队操作:使用poll()或remove()方法从队列的头部获取并移除元素。poll()方法如果队列为空则会返回null,而remove()方法则会抛出异常。
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
queue.add(2);
int item = queue.poll(); // item的值为1
int item2 = queue.remove(); // item2的值为23.判断队列是否为空
判断队列是否为空:使用isEmpty()方法判断队列是否为空。
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
boolean isEmpty = queue.isEmpty(); // isEmpty的值为false4.获取队列大小
获取队列大小:使用size()方法获取队列的大小。
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
queue.add(2);
int size = queue.size(); // size的值为25.其它
除了以上常用的操作外,Java的Queue接口还提供了其他一些方法,如element()方法用于获取队列的头元素但不移除,peek()方法用于获取队列头元素但不移除且判断队列是否为空等。可以根据具体需求选择适合的方法使用。

优先级队列(堆)
1. 优先级队列概念
前面介绍过队列,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话;初中那会班主任排座位时可能会让成绩好的同学先挑座位。
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。堆实现了Queue这个接口,可以把它当做优先级队列
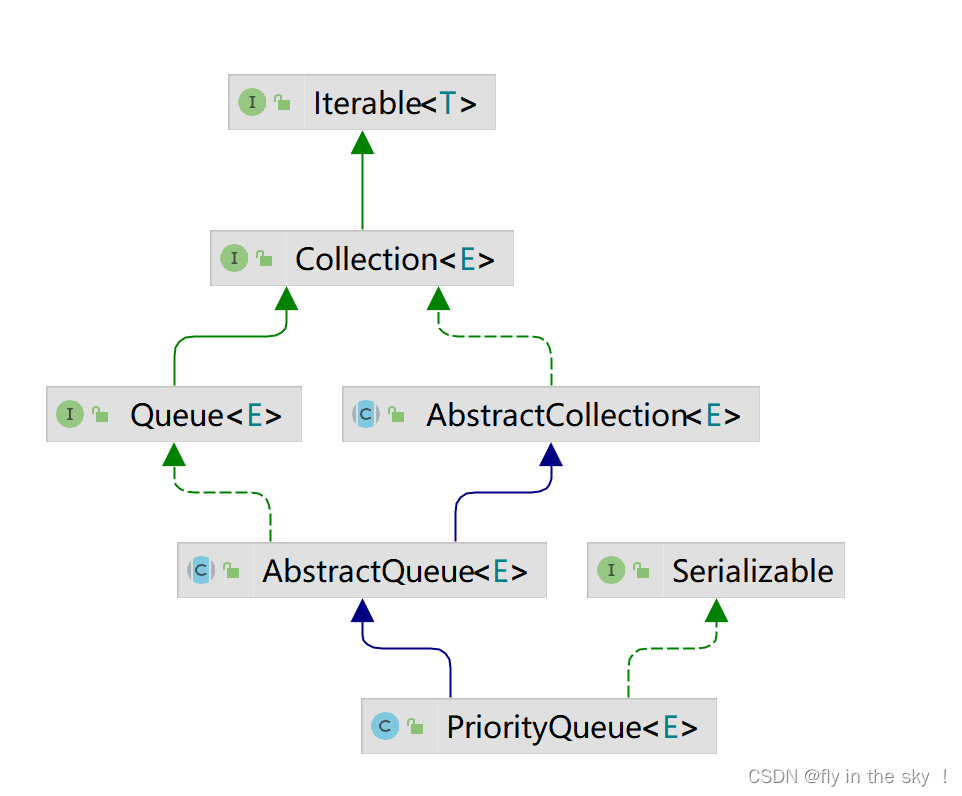

Java中的优先级队列(PriorityQueue)是一种特殊的队列,它使用二叉堆实现。在优先级队列中,每个元素都有一个优先级,优先级越高的元素在队列中的位置越靠前。
Java中的PriorityQueue具有以下特点
插入操作:向PriorityQueue中插入元素时,会根据元素的优先级确定其位置。如果新插入的元素的优先级高于当前队列中的最高优先级元素,则新元素将成为队列中的最高优先级元素。
删除操作:从PriorityQueue中删除元素时,会删除具有最高优先级的元素。如果队列中有多个具有相同最高优先级的元素,则会按照它们在队列中的顺序删除。
可查找操作:PriorityQueue支持查找操作,可以查找具有最高优先级的元素,或者查找具有指定优先级的元素。
2.常用的PriorityQueue操作
以下是一些常用的PriorityQueue操作
1.PriorityQueue的创建
在Java中,PriorityQueue可以使用以下代码创建:
PriorityQueue<Integer> pq = new PriorityQueue<>();2.插入元素
可以使用add()方法向PriorityQueue中插入元素,例如:
pq.add(3);
pq.add(1);
pq.add(2);3.删除具有最高优先级的元素
可以使用poll()方法从PriorityQueue中删除具有最高优先级的元素,例如:
int max = pq.poll(); // max = 34.查找具有最高优先级的元素
可以使用peek()方法查找具有最高优先级的元素,例如:
java
int max = pq.peek(); // max = 35.其它
除了默认的PriorityQueue外,Java还提供了一些其他类型的PriorityQueue,例如ArrayDeque、LinkedBlockingDeque等。这些PriorityQueue的实现方式略有不同,可以根据实际需求选择适合的类型。

3. 优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整,本质上堆是一棵顺序存储的二叉树
Java中的优先级队列(PriorityQueue)是使用二叉堆实现的一种数据结构。二叉堆是一种特殊的树形数据结构,其中每个节点都满足堆的性质:根节点的值小于或等于其子节点的值(最大堆)或根节点的值大于或等于其子节点的值(最小堆)。
虽然Java中的PriorityQueue是使用二叉堆实现的,但我们可以使用其他数据结构来模拟实现优先级队列。
下面是一种使用数组实现优先级队列的示例代码:
public class PriorityQueue<T extends Comparable<T>> {private int[] heap;private int size;public PriorityQueue(int capacity) {heap = new int[capacity + 1];}public void enqueue(T value) {if (size == heap.length - 1) {resize();}int index = size;heap[index] = value.compareTo(((T) heap[index - 1])) > 0 ? value : heap[index - 1];upHeap(index);size++;}public T dequeue() {if (size == 0) {throw new IllegalStateException("Priority queue is empty");}T max = (T) heap[0];heap[0] = heap[size - 1];size--;downHeap(0);return max;}private void resize() {int[] newHeap = new int[heap.length * 2];System.arraycopy(heap, 0, newHeap, 0, heap.length);heap = newHeap;}private void upHeap(int index) {while (index > 0) {int parentIndex = (index - 1) / 2;if (heap[parentIndex].compareTo((T) heap[index]) <= 0) {break;}swap(parentIndex, index);index = parentIndex;}}private void downHeap(int index) {int size = heap.length - 1;while (true) {int leftChildIndex = 2 * index + 1;int rightChildIndex = 2 * index + 2;int largestIndex = index;if (leftChildIndex < size && heap[leftChildIndex].compareTo((T) heap[largestIndex]) > 0) {largestIndex = leftChildIndex;}if (rightChildIndex < size && heap[rightChildIndex].compareTo((T) heap[largestIndex]) > 0) {largestIndex = rightChildIndex;}if (largestIndex == index) {break;}swap(index, largestIndex);index = largestIndex;}}private void swap(int i, int j) {Object temp = heap[i];heap[i] = heap[j];heap[j] = temp;}
}注:该代码定义了一个泛型的PriorityQueue类,支持向队列中插入元素(enqueue)和从队列中删除元素(dequeue)的操作。PriorityQueue使用一个数组来模拟二叉堆,通过调整数组元素的位置来维护堆的性质。在插入元素时,使用upHeap方法调整数组元素的位置,以维护最大堆的性质;在删除元素时,使用downHeap方法调整数组元素的位置,以维护最大堆的性质。在需要获取队列中的最大元素时,始终返回数组的第一个元素即可。
堆
1.堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一
个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大
堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
2.堆的性质
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。
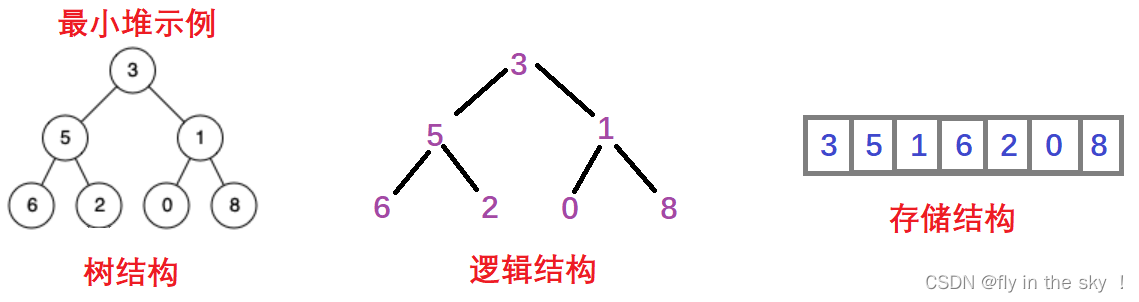

3.堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,

注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
将元素存储到数组中后,可以对树进行还原。
- 假设i为节点在数组中的下标,则有:
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
4.堆的创建
问题:对于集合{ 0,1,2,3,5,68 }中的数据,如果将其创建成最大堆呢?
1.如何把给定的一棵二叉树,变成最小堆或者最大堆
以变成最大堆为例
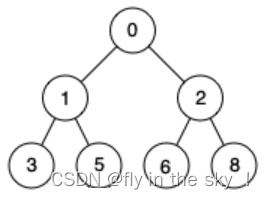
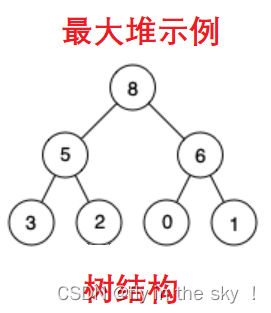
从这棵树的最后一棵子树开始调整,从右往左,从上往下
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
向下过程(以最大堆为例):
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在,即:child > size, 进行以下操作,直到parent的左孩子不存在
parent右孩子是否存在,存在找到左右孩子中较大的孩子,让child进行标计,
将parent与较大的孩子child比较,如果:parent大于较大的孩子child,调整结束
否则:交换parent与较大的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子树不满足最大堆的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续。

public class MaxHeapify {private int[] heap; // 存储二叉树节点的数组private int size; // 二叉树的大小public MaxHeapify(int n) {heap = new int[n + 1]; // 创建一个大小为 n+1 的数组,因为数组下标从0开始size = 0; // 二叉树的大小初始为0}public void add(int val) {heap[++size] = val; // 将新节点插入到数组的末尾int i = size; // 当前节点下标while (i > 1 && heap[i / 2] < heap[i]) { // 如果当前节点不是根节点且当前节点的值大于根节点的值swap(i, i / 2); // 则交换当前节点和根节点i /= 2; // 重新获取当前节点下标}}public int get(int i) {return heap[i]; // 返回指定下标的节点的值}public void maxHeapify(int i) { // i表示当前节点的下标int left = 2 * i + 1; // 左子节点的下标int right = 2 * i + 2; // 右子节点的下标int largest = i; // 记录最大的节点下标if (left < size && heap[left] > heap[largest]) { // 如果左子节点存在且值大于当前最大值largest = left; // 更新最大值下标为左子节点下标}if (right < size && heap[right] > heap[largest]) { // 如果右子节点存在且值大于当前最大值largest = right; // 更新最大值下标为右子节点下标}if (largest != i) { // 如果当前节点不是最大值节点swap(i, largest); // 则交换当前节点和最大值节点maxHeapify(largest); // 对新的当前节点进行最大堆调整}}private void swap(int i, int j) { // i和j分别表示两个节点的下标int temp = heap[i]; // 保存第一个节点的值heap[i] = heap[j]; // 将第二个节点的值赋给第一个节点heap[j] = temp; // 将第一个节点的值赋给第二个节点}
}/*注释:
private int[] heap; 和 private int size; 分别表示存储二叉树节点的数组和二叉树的大小。
public MaxHeapify(int n) 是构造函数,创建一个大小为 n+1 的数组,因为数组下标从0开始。
public void add(int val) 方法将新节点插入到数组的末尾,然后通过交换节点和其父节点来调整二叉树,使其满足最大堆的性质。
public int get(int i) 方法返回指定下标的节点的值。
public void maxHeapify(int i) 方法用于调整以 i 为根节点的子树为最大堆。首先找到左右子节点中最大的节点,然后与当前节点进行交换,并对新的当前节点进行最大堆调整。这个方法使用了递归的方式,直到每个子树都是最大堆为止。
private void swap(int i, int j) 方法用于交换两个节点的值。*/ public void shiftDown(int[] array, int parent) {// child先标记parent的左孩子,因为parent可能右左没有右int child = 2 * parent + 1;int size = array.length;while (child < size) {// 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记if (child + 1 < size && array[child + 1] < array[child]) {{child += 1;}}// 如果双亲比其最小的孩子还小,说明该结构已经满足堆的特性了if (array[parent] <= array[child]) {break;} else {// 将双亲与较小的孩子交换int t = array[parent];array[parent] = array[child];array[child] = t;// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整parent = child;child = parent * 2 + 1;}}}注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
2.时间复杂度分析
时间复杂度分析:最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为O(log2n)
建堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是
近似值,多几个节点不影响最终结果):

因此:建堆的时间复杂度为O(N)。
堆的插入与删除
2.4.1 堆的插入
堆的插入总共需要两个步骤:
1. 先将元素放入到底层空间中(注意:空间不够时需要扩容)
2. 将最后新插入的节点向上调整,直到满足堆的性质
public void shiftUp(int child) {// 找到child的双亲int parent = (child - 1) / 2;while (child > 0) {// 如果双亲比孩子大,parent满足堆的性质,调整结束if (array[parent] > array[child]) {break;} else {// 将双亲与孩子节点进行交换int t = array[parent];array[parent] = array[child];array[child] = t;// 小的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增child = parent;parent = (child - 1) / 1;}}
}5.堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
3. 对堆顶元素进行向下调整

6.用堆模拟实现优先级队列
public class MyPriorityQueue {// 演示作用,不再考虑扩容部分的代码private int[] array = new int[100];private int size = 0;public void offer(int e) {array[size++] = e;shiftUp(size - 1);}public int poll() {int oldValue = array[0];array[0] = array[--size];shiftDown(0);return oldValue;}public int peek() {return array[0];}
}7.常用接口介绍
PriorityQueue的特性:Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的,主要介绍的是PriorityQueue。

1.关于PriorityQueue的使用注意事项
关于PriorityQueue的使用要注意:
1. 使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue;
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出
ClassCastException异常
3. 不能插入null对象,否则会抛出NullPointerException
4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
5. 插入和删除元素的时间复杂度为
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
3.2 PriorityQueue常用接口介绍
1. 优先级队列的构造
PriorityQueue中常见的几种构造方式

public static void TestPriorityQueue() {// 创建一个空的优先级队列,底层默认容量是11PriorityQueue<Integer> q1 = new PriorityQueue<>();// 创建一个空的优先级队列,底层的容量为initialCapacityPriorityQueue<Integer> q2 = new PriorityQueue<>(100);ArrayList<Integer> list = new ArrayList<>();list.add(4);list.add(3);list.add(2);list.add(1);// 用ArrayList对象来构造一个优先级队列的对象// q3中已经包含了三个元素PriorityQueue<Integer> q3 = new PriorityQueue<>(list);System.out.println(q3.size());System.out.println(q3.peek());}注意:默认情况下,PriorityQueue队列是小堆,如果需要大堆需要用户提供比较器
public class TestPriorityQueue {public static void main(String[] args) {PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());p.offer(4);p.offer(3);p.offer(2);p.offer(1);p.offer(5);System.out.println(p.peek());}
}此时创建出来的就是一个大堆。
2. 插入/删除/获取优先级最高的元素
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时间复杂度O(log2N),注意:空间不够时候会进行扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll() | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
public static void TestPriorityQueue2() {int[] arr = {4, 1, 9, 2, 8, 0, 7, 3, 6, 5};// 一般在创建优先级队列对象时,如果知道元素个数,建议就直接将底层容量给好// 否则在插入时需要不多的扩容// 扩容机制:开辟更大的空间,拷贝元素,这样效率会比较低PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);for (int e : arr) {q.offer(e);}System.out.println(q.size()); // 打印优先级队列中有效元素个数System.out.println(q.peek()); // 获取优先级最高的元素// 从优先级队列中删除两个元素之和,再次获取优先级最高的元素q.poll();q.poll();System.out.println(q.size()); // 打印优先级队列中有效元素个数System.out.println(q.peek()); // 获取优先级最高的元素q.offer(0);System.out.println(q.peek()); // 获取优先级最高的元素// 将优先级队列中的有效元素删除掉,检测其是否为空q.clear();if (q.isEmpty()) {System.out.println("优先级队列已经为空!!!");} else {System.out.println("优先级队列不为空");}}注意:以下是JDK 1.8中,PriorityQueue的扩容方式:
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;private void grow(int minCapacity) {int oldCapacity = queue.length;// Double size if small; else grow by 50%int newCapacity = oldCapacity + ((oldCapacity < 64) ?(oldCapacity + 2) :(oldCapacity >> 1));// overflow-conscious codeif (newCapacity - MAX_ARRAY_SIZE > 0)newCapacity = hugeCapacity(minCapacity);queue = Arrays.copyOf(queue, newCapacity);}private static int hugeCapacity(int minCapacity) {if (minCapacity < 0) // overflowthrow new OutOfMemoryError();return (minCapacity > MAX_ARRAY_SIZE) ?Integer.MAX_VALUE :MAX_ARRAY_SIZE;}优先级队列的扩容说明:
如果容量小于64时,是按照oldCapacity的2倍方式扩容的
如果容量大于等于64,是按照oldCapacity的1.5倍方式扩容的
如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容
完结撒花✿✿ヽ(°▽°)ノ✿

相关文章:

一万字关于java数据结构堆的讲解,让你从入门到精通
目录 java类和接口总览 队列(Queue) 1. 概念 2. 队列的使用 以下是一些常用的队列操作: 1.入队操作 2.出队操作 3.判断队列是否为空 4.获取队列大小 5.其它 优先级队列(堆) 1. 优先级队列概念 Java中的PriorityQueue具有以下特点 2.常用的PriorityQue…...

Java集合底层源码剖析-ArrayList和LinkedList
文章目录 ArrayList基本原理优缺点核心方法的原理数组扩容以及元素拷贝LinkedList基本原理优缺点双向链表数据结构插入元素的原理获取元素的原理删除元素的原理Vector和Stack栈数据结构的源码剖析ArrayList 基本原理 ArrayList是Java中的一个非常常用的数据结构,它实现了Lis…...

【数据分享】2006-2021年我国城市级别的市政公用设施建设固定资产投资相关指标(30多项指标)
《中国城市建设统计年鉴》中细致地统计了我国城市市政公用设施建设与发展情况,在之前的文章中,我们分享过基于2006-2021年《中国城市建设统计年鉴》整理的2006—2021年我国城市级别的市政设施水平相关指标(可查看之前的文章获悉详情ÿ…...
学点Selenium玩点新鲜~,让分布式测试有更多玩法
前 言 我们都知道 Selenium 是一款在 Web 应用测试领域使用的自动化测试工具,而 Selenium Grid 是 Selenium 中的一大组件,通过它能够实现分布式测试,能够帮助团队简单快速在不同的环境中测试他们的 Web 应用。 分布式执行测试其实并不是一…...
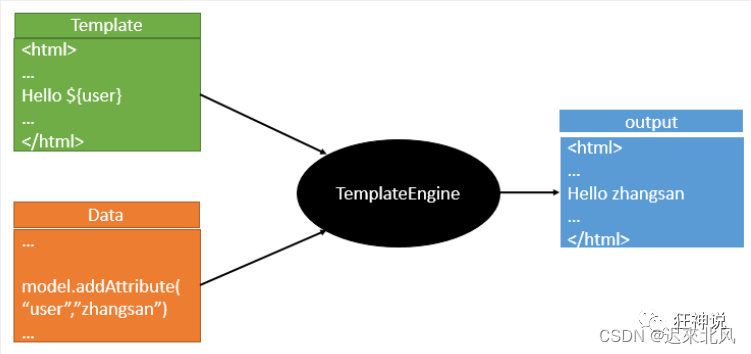
【SpringBoot学习笔记】04. Thymeleaf模板引擎
模板引擎 所有的html元素都可以被thymeleaf替换接管 th:元素名 templates下的只能通过Controller来跳转,templates前后端分离,需要模板引擎thymeleaf支持 模板引擎的作用就是我们来写一个页面模板,比如有些值呢,是动态的&#x…...

【uni-app】 .sync修饰符与$emit(update:xxx)实现数据双向绑定
最近在看uni-app文档,看到.sync修饰符的时候,觉得很有必要记录一下 其实uni-app是一个基于Vue.js和微信小程序开发框架的跨平台开发工具 所以经常会听到这样的说法,只要你会vue,uni-app就不难上手 在看文档的过程中,发…...
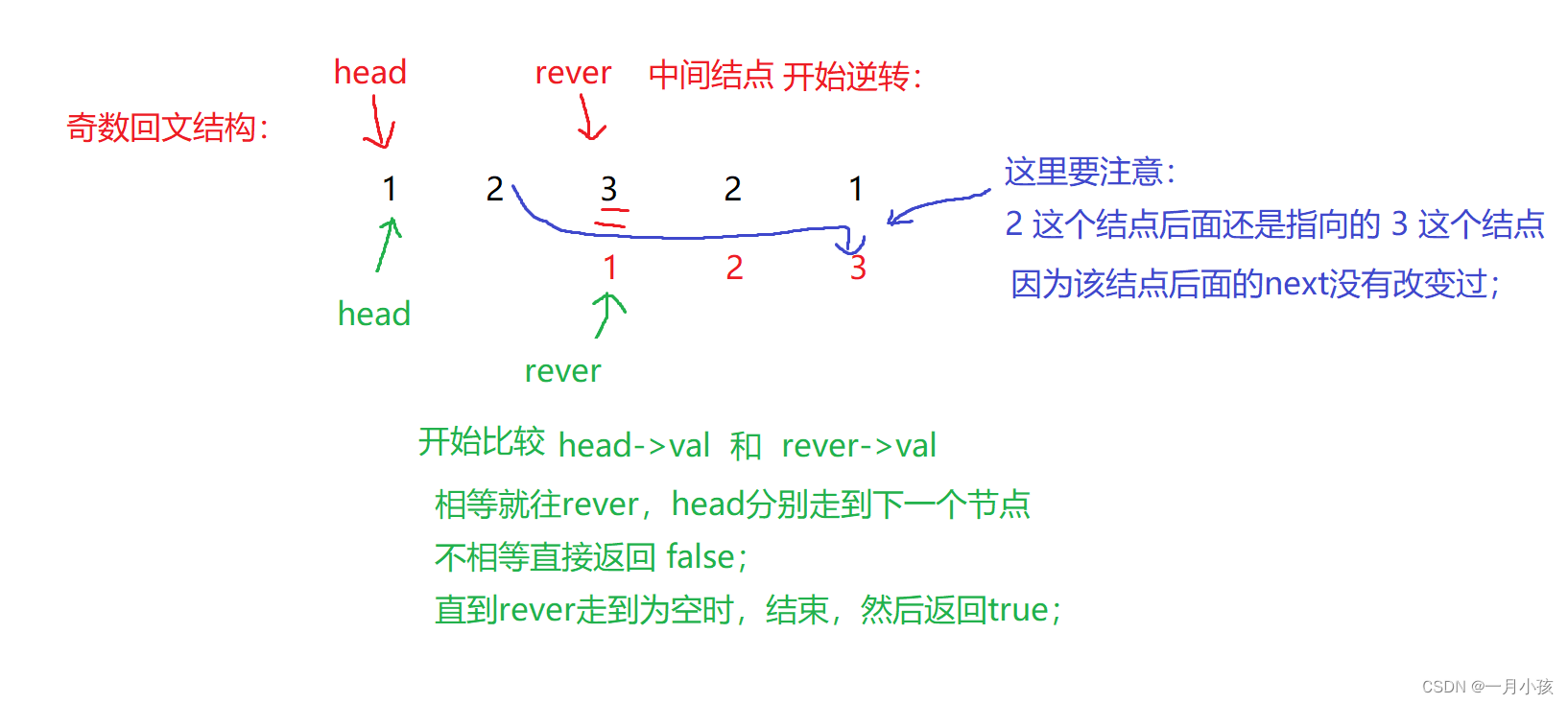
链表之第二回
欢迎来到我的:世界 该文章收入栏目:链表 希望作者的文章对你有所帮助,有不足的地方还请指正,大家一起学习交流 ! 目录 前言第一题:反转一个链表第二题:链表内指定区间反转第三题:判断一个链表…...

【sgDragSize】自定义拖拽修改DIV尺寸组件,适用于窗体大小调整
核心原理就是在四条边、四个顶点加上透明的div,给不同方向提供按下移动鼠标监听 ,对应计算宽度高度、坐标变化 特性: 支持设置拖拽的最小宽度、最小高度、最大宽度、最大高度可以双击某一条边,最大化对应方向的尺寸;再…...

Gson与FastJson详解
Gson与FastJson详解 Java与JSON 做什么? 将Java中的对象 快速的转换为 JSON格式的字符串. 将JSON格式的字符串, 转换为Java的对象. Gson 将对象转换为JSON字符串 转换JSON字符串的步骤: 引入JAR包 在需要转换JSON字符串的位置编写如下代码即可: String json new Gson().to…...
LeetCode150道面试经典题-- 有效的字母异位词(简单)
1.题目 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 2.示例 s"adasd" t"daads" 返回true s"addad" t &q…...

前端与人工智能
前端开发与人工智能的结合在未来将会产生许多有趣和有前景的发展。以下是前端与人工智能结合可能带来的一些趋势和前景: 智能用户体验:人工智能可以用于改善用户体验,例如通过个性化推荐、情感分析等技术来提供更贴近用户需求的内容和功能。…...
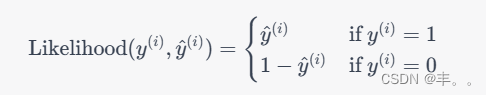
神经网络基础-神经网络补充概念-14-逻辑回归中损失函数的解释
概念 逻辑回归损失函数是用来衡量逻辑回归模型预测与实际观测之间差异的函数。它的目标是找到一组模型参数,使得预测结果尽可能接近实际观测。 理解 在逻辑回归中,常用的损失函数是对数似然损失(Log-Likelihood Loss)ÿ…...
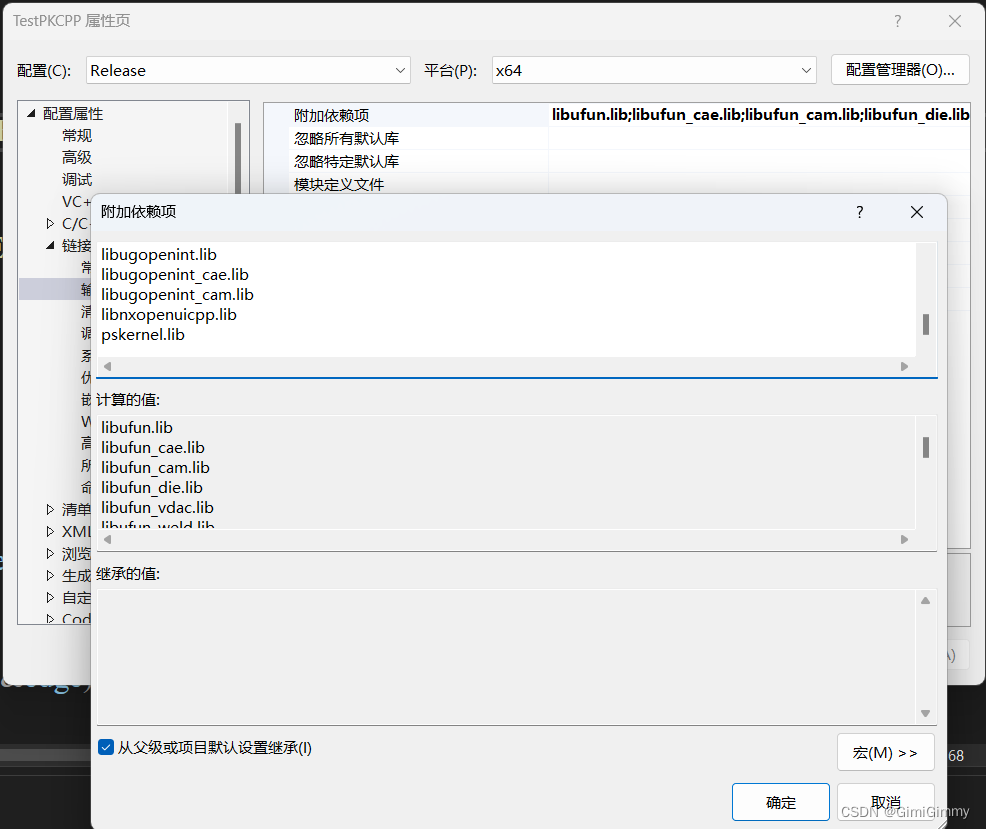
UG NX二次开发(C++)-PK函数创建一条圆弧曲线
文章目录 1、前言2、创建一个项目3、添加头文件4、在do_it中添加创建圆曲线的源代码5、调用dll6、再创建一个长方体验证1、前言 采用PK进行UG NX二次开发,现在看到的文章很多是直接创建实体,然后在UG NX的视图区显示出来,对于创建圆曲线的文章不多,本文讲一下PK函数创建圆…...

AndroidStudio中修改打包生成的apk名称
1.配置手机架构 splits {abi {enable truereset()include armeabi-v7a,arm64-v8auniversalApk false} } 2.多渠道 productFlavors {normal {applicationId "*****"manifestPlaceholders [appName: "string/app_name_normal"]}driver {applicationId &qu…...
)
多个springboot整合使用rabbitmq(使用注解的方式)
一、简述 先参考单个springboot使用rabbitmq和了解rabbitmq的五种模式 单个springboot整合rabbitmq_java-zh的博客-CSDN博客 二、创建项目 1、先创建两个springboot项目,一个做生产者,一个做消费者 2、导包(生产者和消费者对应的内容都是一样) <…...

《Effective C++中文版,第三版》读书笔记2
条款06:若不想使用编译器自动生成的函数,就该明确拒绝 为驳回编译器自动()提供的机能,可将相应的成员函数声明为私有的,同时不实现它。 #include <iostream>class MyClass { public:MyClass(int in…...

虫情测报系统的工作原理及功能优势
KH-CQPest虫情测报系统能够在不对虫体造成任何破坏的情况下,无公害的杀死虫子,利用高倍显微镜和高清摄像头拍摄虫体照片,并将虫体照片发送到远端平台,让工作人员无需要到现场,通过平台就可以观察害虫的种类和数量&…...

UWB定位技术详细介绍
UWB(Ultra-Wideband)定位技术是一种通过利用信号的超宽频带特性进行高精度定位的技术。其原理是通过测量信号在空间传播中的时间延迟差异来计算物体的位置。 UWB技术与传统无线通信技术不同,它利用非常宽的频带进行通信,通常超过…...
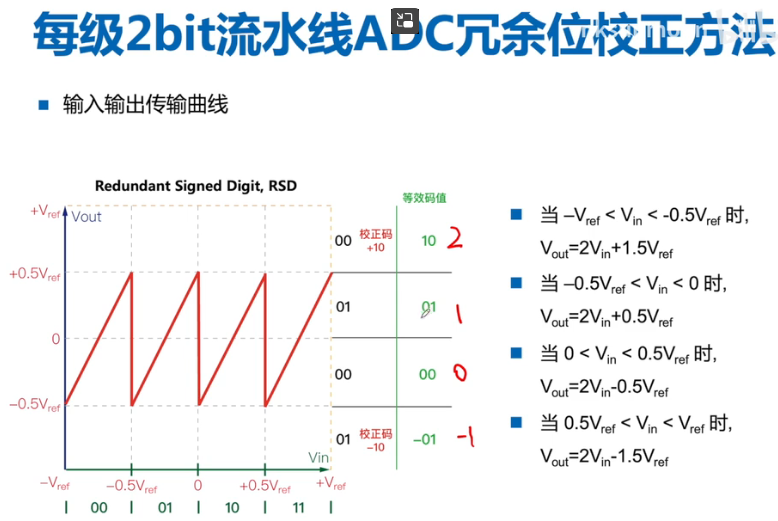
PiplineADC学习一:
PiplineADC结构: PiplineADC起源之FlashADC PiplineADC起源之Sub-Ranging-ADC 比较器存在失调: 因此每级1bit不实用,需要做冗余位设计。 多比较一次,两个阈值,三个区间,分别对于输出00,01,10。正常2bit应该…...

Linux elasticsearch设置为开机自启动服务
Linux elasticsearch怎么设置为设置为开机自启动服务 1、进入/etc/init.d目录 cd /etc/init.d 2、新建文件elasticsearch,注意,没有扩展名 vi elasticsearch 3、新建文件elasticsearch的内容如下 说明: (1)“su…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
