归并排序 与 计数排序
目录
1.归并排序
1.1 递归实现归并排序:
1.2 非递归实现归并排序
1.3 归并排序的特性总结:
1.4 外部排序
2.计数排序
2.1 操作步骤:
2.2 计数排序的特性总结:
3. 7种常见比较排序比较
1.归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序核心步骤:

动图演示:

1.1 递归实现归并排序:
归并排序类似于二叉树中的后序遍历,先让整个数组分为两个子序列,归并这两部份子序列,但是归并需要两部份子序列有序,然后取小的尾插到一个新开辟的数组中,归并完成后后再拷贝回原数组,如何让子序列有序,还要再次将每个子序列分为两部分,直到每个子序列只有一个值,这时已经递归到最深处,然会递归向回归并。
递归代码实现:
//归并排序
//开辟好空间后由下面元素调用此函数
void _MergeSort(int* arr, int* tmp, int begin, int end)
{if (begin == end){return;}int midi = (begin + end) / 2;_MergeSort(arr, tmp, begin, midi);_MergeSort(arr, tmp, midi+1, end);int begin1 = begin;int end1 = midi;int begin2 = midi + 1;int end2 = end;int i = begin;//归并 取小的尾插到开辟的空间while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] <= arr[begin2]){tmp[i++] = arr[begin1++];}else{tmp[i++] = arr[begin2++];}}while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}//将归并好的两组数据拷贝会原数组memcpy(arr + begin, tmp + begin, sizeof(int) * (end - begin + 1));}void MergeSort(int* arr, int n)
{//开辟空间int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(arr, tmp, 0, n - 1);
}
小区间优化
//小区间优化
if (end - begin +1<10)
{//使用插入排序InsertSort(arr + begin, end - begin + 1);return;
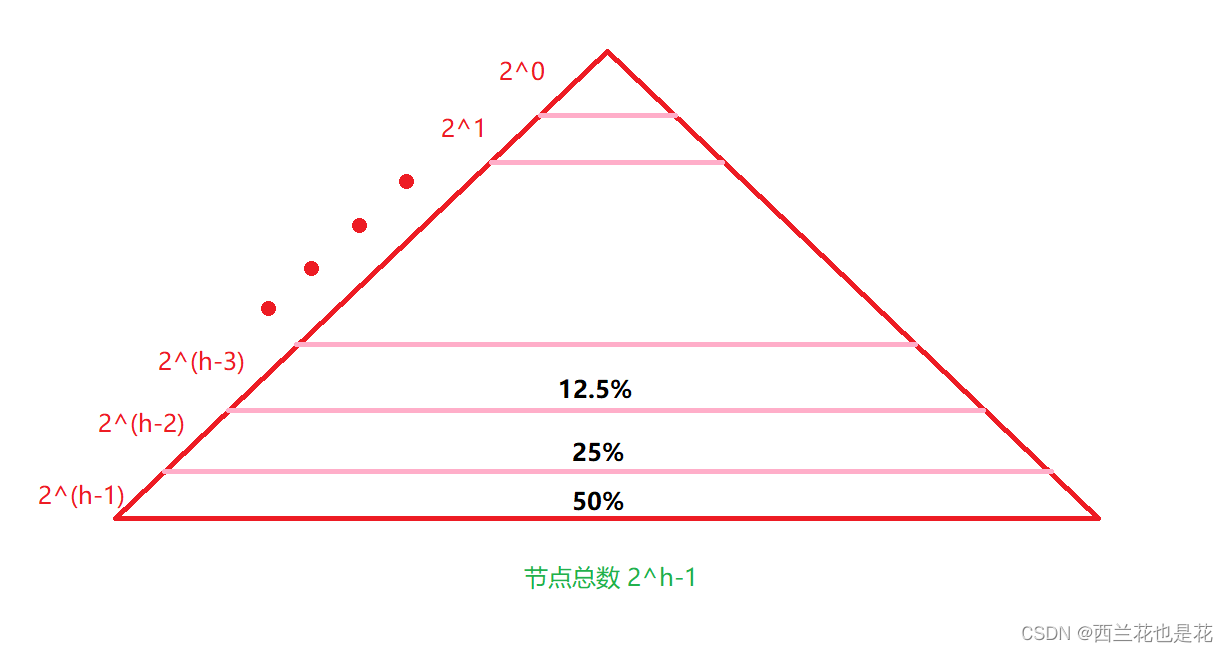
}优化的本质是减小递归调用的次数,由于二叉树的性质。我们可以得出满二叉树后三层大约占总个数的85%。为了减小递归开销,我们可以将小区间的递归调用改为直接插入排序,可以提高一点排序的性能,但也不会提高很多。快排也可以使用这种方式优化。
1.2 非递归实现归并排序
我们可以先让每组gap=1个数据,每次归并两组,然后在让gap*=2,再次归并,直到gap>n。
代码实现:
//非递归实现归并排序
void MergeSortNonR1(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//每组有gap个数据,归并两组int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n || begin2 >= n)//不需要归并{break;}//修正if (end2 >= n){end2 = n - 1;}//归并while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] <= arr[begin2]){tmp[j++] = arr[begin1++];}else{tmp[j++] = arr[begin2++];}}while (begin1 <= end1){tmp[j++] = arr[begin1++];}while (begin2 <= end2){tmp[j++] = arr[begin2++];}//将归并后的两组数据 拷贝回原数组 memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}
}边界越界问题:
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;begin1不会越界,因为begin1 = i,i 复合循环条件 。
- end1,begin2,end2都越界
- begin2,end2越界
- end2越界
1. end1,begin2,end2都越界
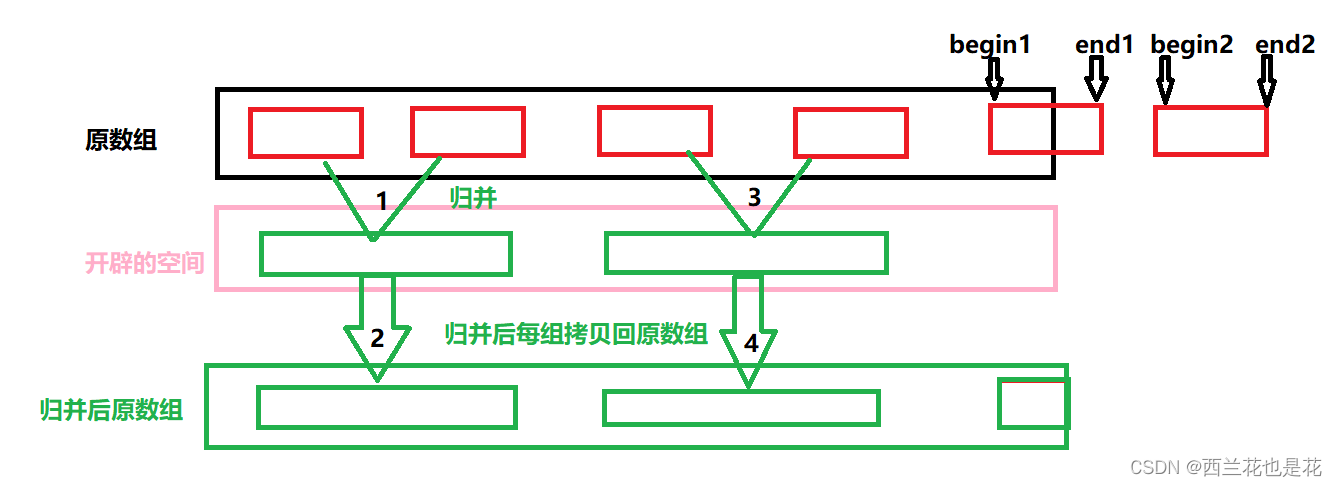
此时不需要归并直接跳出循环。
2. begin2,end2越界
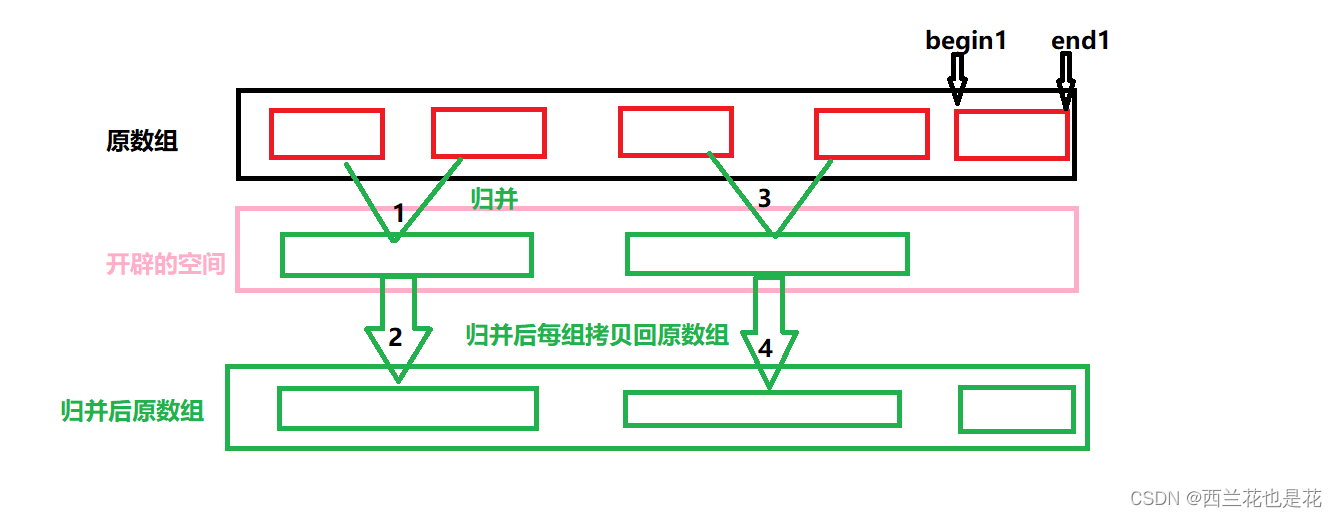
此时也不需要归并直接跳出循环。
3. end2越界
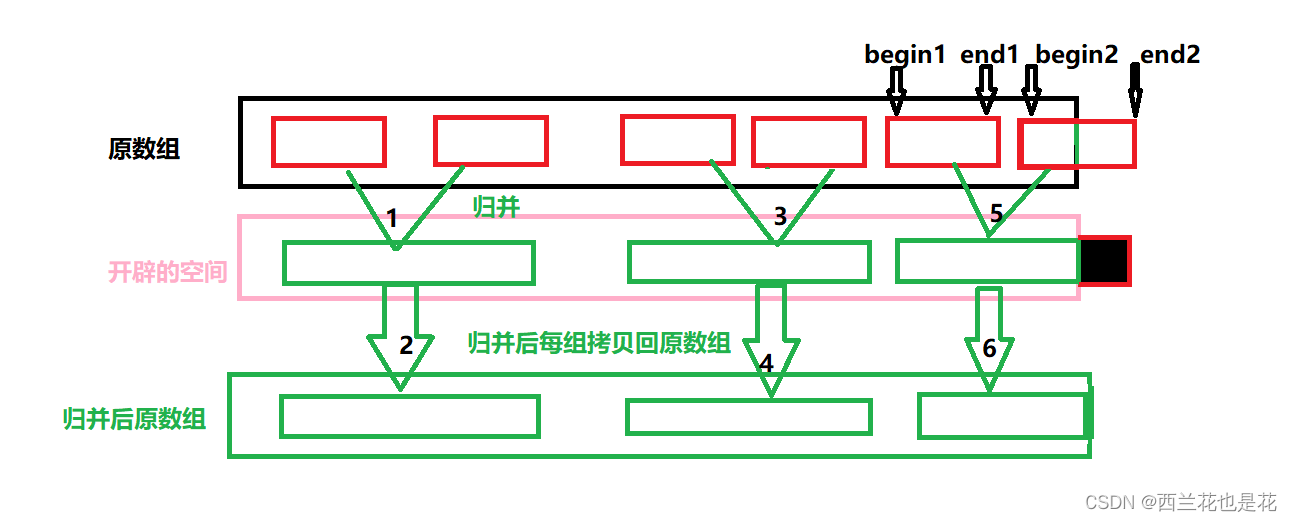
此时需要归并,但是我们要修改end2,将end2改为n-1。
代码:
if (end1 >= n || begin2 >= n)//不需要归并{break;}//修正if (end2 >= n){end2 = n - 1;}1.3 归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
1.4 外部排序
概念:当数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
在我们所学的排序算法中,只有非递归归并排序的思想可以用于外部排序。其他排序算法都只适用于内部排序,因为他们都使用了下标来进行随机存取,而非递归归并排序不需要,是顺序存取,这里举个例子:
假如我们由100亿个整数要排序,也就是大约40G,而我们的内存中只有1G,步骤:
- 把40G的文件分为40份。
- 让每份文件依次放到内部中排序,让40份文件内部有序。
- 两两归并,分别从两个文件中读一个数据,然后选小的写文件,这时就与非递归归并排序相同了。
2.计数排序
思想:计数排序又称为鸽巢原理,是一种非比较排序,是对哈希直接定址法的变形应用。
2.1 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中

代码实现:
// 计数排序
void CountSort(int* arr, int n)
{//遍历 确定最大值与最小值int max = arr[0];int min = arr[0];for (int i = 0; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//遍历计数int range = max - min + 1;int* CountA = (int*)malloc(sizeof(int) * range);memset(CountA, 0, sizeof(int) * range);for (int i = 0; i < n; i++){CountA[arr[i] - min]++;}//回收到原数组int j = 0;for (int i = 0; i < range; i++){while (CountA[i]--){arr[j++] = i + min;}}
}2.2 计数排序的特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
3. 7种常见比较排序比较
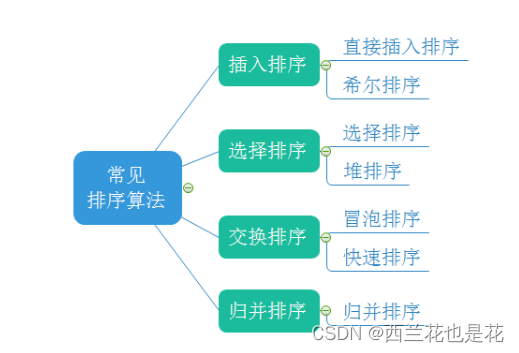
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 简单选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(NlogN)~O(N^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(NlogN) | O(NlogN) | O(N*logN) | O(1) | 不稳定 |
| 归并排序 | O(NlogN) | O(NlogN) | O(N*logN) | O(n) | 稳定 |
| 快速排序 | O(NlogN) | O(NlogN) | O(N^2) | O(logn)~O(n) | 不稳定 |
本篇结束!
相关文章:

归并排序 与 计数排序
目录 1.归并排序 1.1 递归实现归并排序: 1.2 非递归实现归并排序 1.3 归并排序的特性总结: 1.4 外部排序 2.计数排序 2.1 操作步骤: 2.2 计数排序的特性总结: 3. 7种常见比较排序比较 1.归并排序 基本思想: 归并排序(MERGE-SORT)是建立在归并操作上的一种…...

机器学习之逻辑回归
import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LogisticRegression # 获得数据 names[Sample code number,Clump Thickness,Uniformity…...

操作符详解上(非常详细)
目录 二进制介绍二进制2进制转10进制10进制转2进制数字2进制转8进制和16进制2进制转8进制2进制转16进制 原码、反码、补码移位操作符左移操作符右移操作符 位操作符:&、|、^逗号表达式 二进制介绍 在初学计算机时我们常常会听到2进制、8进制、10进制、16进制……...

React 高阶组件(HOC)
React 高阶组件(HOC) 高阶组件不是 React API 的一部分,而是一种用来复用组件逻辑而衍生出来的一种技术。 什么是高阶组件 高阶组件就是一个函数,且该函数接受一个组件作为参数,并返回一个新的组件。基本上,这是从 React 的组成…...
【NepCTF2023】复现
文章目录 【NepCTF2023】复现MISC与AI共舞的哈夫曼codesc语言获取环境变量 小叮弹钢琴陌生的语言你也喜欢三月七么Ez_BASIC_IImisc参考 WEBez_java_checkinPost Crad For You独步天下配置环境独步天下-镜花水月环境变量提权 独步天下-破除虚妄总结 独步天下-破除试炼_加冕成王知…...

大文件切片上传
创建组件:创建一个组件用于处理文件上传,命名为Upload.vue。 <template><div><input type"file" change"handleFileChange" /><button click"startUpload">开始上传</button></div> …...
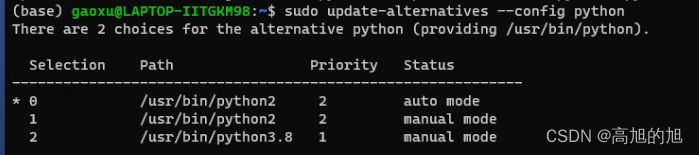
ubuntu切换python版本
在没有安装类似anoconda的管理工具的时候,我们常常会被Ubuntu下的Python版本切换问题所头疼。 可以使用update-alternatives工具进行python版本的任意切换 当使用update-alternatives工具来切换Ubuntu系统上的Python版本时,您实际上是在系统范围内选择…...

docker 安装 elasticsearch、kibana 7.4.2
切换root 用户 su root 拉起镜像 docker pull elasticsearch:7.4.2 docker pull kibana:7.4.2 #1、创建Elasticsearch配置文件夹 mkdir -p /mydata/elasticsearch/config #2、创建Elasticsearch数据文件夹 mkdir -p /mydata/elasticsearch/data #3、创建Elasticsearch插件…...

【es6】函数参数设置默认值
1、es6之前的函数参数默认值写法 1.1、使用短路或||的写法 当y为空时,y判断为false ,走||右边的,所以y world;当y不为空时,y判断为true,不需要再运行||右边的,所以 y y function log(x, y) {y y || W…...

Pytest和Unittest测试框架的区别?
如何区分这两者,很简单unittest作为官方的测试框架,在测试方面更加基础,并且可以再次基础上进行二次开发,同时在用法上格式会更加复杂;而pytest框架作为第三方框架,方便的地方就在于使用更加灵活࿰…...
)
C#基础知识(一)
一、C#程序结构 《1》命名空间的声明(namespace declaration) 《2》一个class 《3》class方法 《4》class属性 《5》一个main方法 《6》语句(statements)&表达式(Expressions) 《7》注释 注:…...
我还不知道?Android组件化插件化模块化
Android组件化、插件化和模块化是针对Android应用程序开发的一种架构设计思想和开发方式。 组件化(Componentization): 组件化是将一个大型的Android应用程序拆分成多个独立的组件(Module),每个组件可以独…...

借助 AI 工具,真的能成为 10x 工程师?
或许你听说过 10x 工程师吗? 如果你问猎头公司 10x 工程师是什么意思,他们可能会说 “生产力”!10x 是指完成任务比别人快 10 倍的工程师。 2019 年,Twitter 上就曾经对 10 x 工程师这一议题有过一次空前热烈的讨论,引…...

TypeScript 面向对象
TypeScript 接口 TypeScript 接口定义如下: interface interface_name { } 以下实例中,我们定义了一个接口 IPerson,接着定义了一个变量 customer,它的类型是 IPerson。 customer 实现了接口 IPerson 的属性和方法。 interf…...

k8s 中快速启动curl pod 做api test
场景 k8s上运行的pod需要进行api测试,由于开发使用的镜像都是最小化构建,不能保证现有的pod中一定有curl工具,于是需要启动一个带有curl工具的测试pod专门进行api测试 指令 kubectl run curl-test-pod --imagecurlimages/curl -n {namespace} -i --tty -- sh上述指令实现在指…...

神经网络基础-神经网络补充概念-56-迁移学习
迁移学习(Transfer Learning)是一种机器学习技术,旨在将在一个任务上学到的知识或模型迁移到另一个相关任务上,以提高新任务的性能。迁移学习的核心思想是通过利用源领域(source domain)的知识来改善目标领…...
)
力扣:65. 有效数字(Python3)
题目: 有效数字(按顺序)可以分成以下几个部分: 一个 小数 或者 整数(可选)一个 e 或 E ,后面跟着一个 整数 小数(按顺序)可以分成以下几个部分: (…...

003-Spring boot 启动流程分析
目录 启动流程分析创建 SpringApplication启动 run(String... args) 读取配置流程分析listeners.environmentPrepared解析配置文件详细分析EnvironmentPostProcessor 详细分析 启动流程分析 SpringApplication.run(App.class, args);return new SpringApplication(primarySour…...
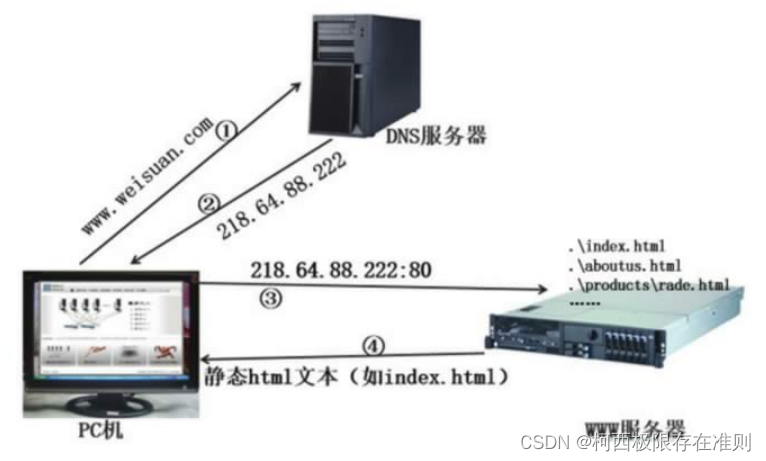
中间件的介绍
1.1 什么是中间件 中间件是介于应用系统和系统软件之间的一类软件,他使用系统软件所提供的基础服务,衔接网络上应用系统的各个部分或不同的应用,能够达到资源共享、功能共享的目的。 例如MySQL就可以看作是具备中间件特性的一种技术&#x…...
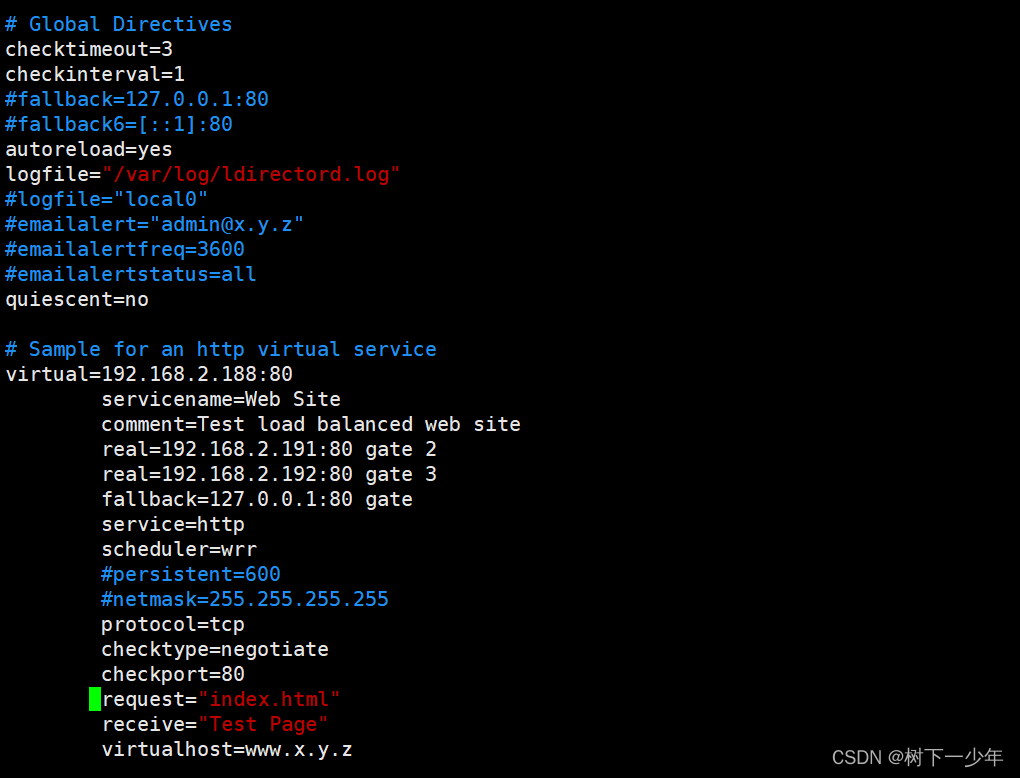
LVS-DR模式下(RS检测)ldirectord工具实现部分节点掉点后将请求发往正常设备进行处理
基于前文的LVS-DR集群构建环境 一.下载ldirectord软件 二.将模板文件中的LVS-DR模式相关文件拷贝到/etc/ha.d主配置目录并按实际设备修改 三.配置两台RS匹配规则 四.停止RS1的http服务进行测试 RS1失去工作能力,RS2接替RS1 基于前文的LVS-DR集群构建环境 一.下…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
