应用层自定义协议(组织数据的格式)
概念
在进行网络传输数据的时候,通常是将要传输的数据组织成一个字符串,再将字符串转换为一个字节流进行网络传输数据,而数据组织的格式是多种多样的,我们只需要保证,客户端和服务器对于字符串的组织和解析统一即可
现有的数据组织格式
由于只需要保证客户端和服务器对于字符串的组织和解析统一即可,所以对于数据的组织格式是多种多样,天马行空的,所以有大佬就提出了现成的数据组织格式
一.xml格式
xml格式例子

上图是xml格式的示例,格式有点像前端的html和css,用了很多的标签采用键值对(key-value)的形式非常清晰的把结构化数据表示出来了
但是缺点也很明显,表示数据需要引入大量的标签,看起来很繁琐,同时由于在进行网络传输的时候标签也需要一起进行传输,所以会占用不少的网络带宽(国内最贵的硬件资源,就是网络带宽)所以现在xml格式以及没有多少地方会使用了
二.json格式
json格式例子

上图是json格式的示例,在json中,使用{ }表示键值对,使用[ ]表示数组,数组里的每一个元素,可以是数字,可以是字符串,还可以是其他的{ }或[ ]
在json数据组织格式中使用的核心思路也是键值对(key-value),很明显,json组织数据的格式比xml清新很多,这是当前最主流使用的一种网络传输数据的格式,未来在实际开发中会经常用到json格式的数据
但是即使是json格式来组织数据依然会引入一些标签,在传输数据的时候占用部分的网络带宽,这也是json格式组织数据的一个小小的缺点
三.protobuffer格式
这是谷歌提出的一套,二进制的数据序列化方式,使用二进制的方式,约定某几个字节,表示哪个属性,这样就不需要引入标签,就可以最大限度的节省空间,就可以在传输数据的时候只传输确实需要的数据,节省网络带宽,最大化效率
但是也有缺点,二进制数据是无法用肉眼观察的,不方便调试,使用起来比较复杂,需要专门编写一个proto文件(有自己一系列的语法规则),描述数据的格式咋样的,再进一步的通过大佬提供的工具,把proto文件转换成一些代码,再嵌入到程序中使用
实际开发中是开发效率重要还是运行效率重要
而在我们实际开发中是开发效率重要还是运行效率重要呢,通常来说是开发效率重要,因为想要提高运行效率,升级硬件也是一种重要手段,不需要花太多的钱,而想要提高开发效率,就得招聘更多的程序猿,在软件开发领域中,人力成本,永远是最贵的,所以通常对于运行效率没有严苛要求的话,我们还是使用json格式来组织数据更多一点
相关文章:

应用层自定义协议(组织数据的格式)
概念 在进行网络传输数据的时候,通常是将要传输的数据组织成一个字符串,再将字符串转换为一个字节流进行网络传输数据,而数据组织的格式是多种多样的,我们只需要保证,客户端和服务器对于字符串的组织和解析统一即可 现…...

5种常见的3D游戏艺术风格及工具栈
在游戏开发领域,3D 艺术风格已成为为玩家创造身临其境、引人入胜的体验的重要组成部分。 随着技术的进步,创造令人惊叹的 3D 视觉效果的可能性已经大大扩展,为游戏开发人员提供了广泛的选择。 在本文中,我们将探讨当今游戏开发中…...
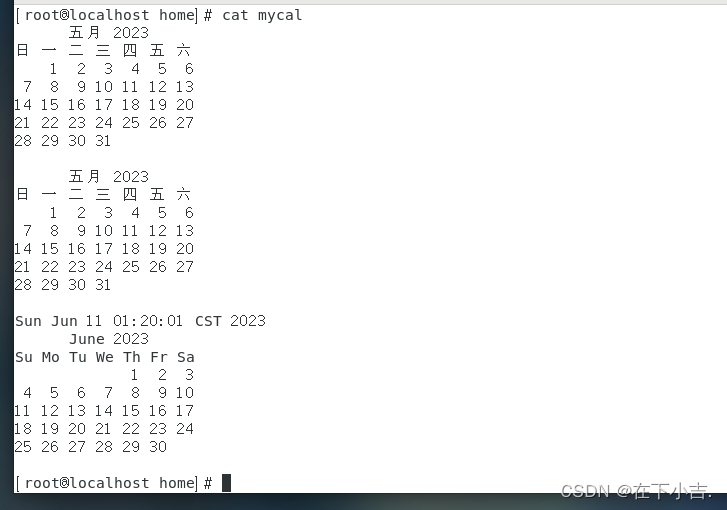
【玩转Linux操作】crond的基本操作
🎊专栏【玩转Linux操作】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【Counting Stars 】 欢迎并且感谢大家指出小吉的问题🥰 文章目录 🍔概述🍔命令⭐常用选项 🍔练…...

设置Linux 静态IP
LInux虚拟机默认的IP地址是动态获取的 作为服务器,我们一般还需要把IP地址设置为静态的 设置静态IP vim /etc/sysconfig/network-scripts/ifcfg-ens33 TYPEEthernet PROXY_METHODnone BROWSER_ONLYno # BOOTPROTOdhcp 动态获取 BOOTPROTOstatic IPADDR"192.16…...
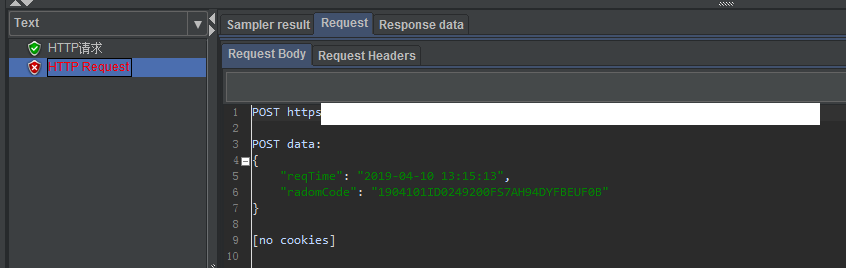
JMeter接口自动化测试实例—JMeter引用javaScript
Jmeter提供了JSR223 PreProcessor前置处理器,通过该工具融合了Java 8 Nashorn 脚本引擎,可以执行js脚本以便对脚本进行前置处理。其中比较典型的应用就是通过执行js脚本对前端数据进行rsa加密,如登录密码加密。但在这里我就简单的应用javaScr…...
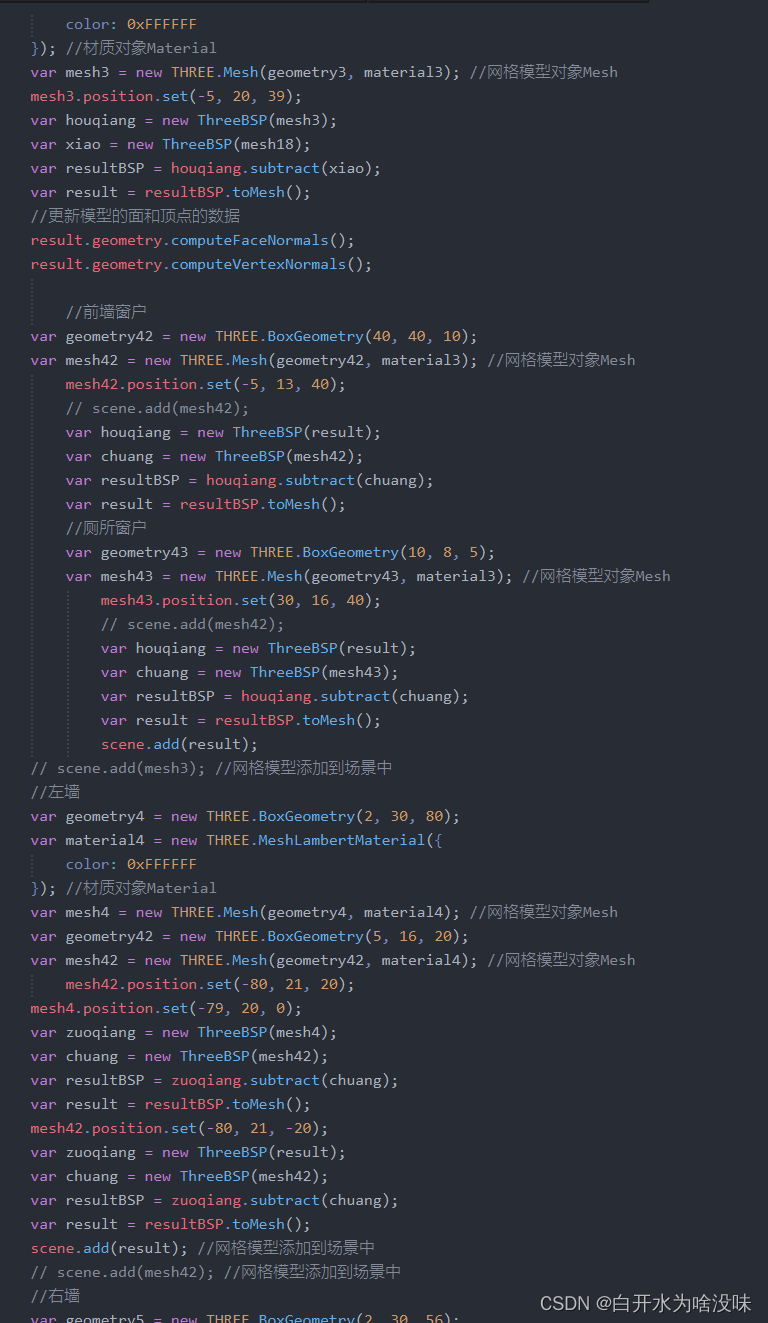
javascript期末作业【三维房屋设计】 【源码+文档下载】
1、引入three.js库 官网下载three.js 库 放置目录并引用 引入js文件: 设置场景(scene) (1)创建场景对象 (2)设置透明相机 1,透明相机的优点 透明相机机制更符合于人的视角,在场景预览和游戏场景多有使用…...

数组详解
1. 一维数组的创建和初始化 1.1 数组的创建 数组是一组相同类型元素的集合。 数组的创建方式: type_t arr_name [const_n]; //type_t 是指数组的元素类型 //const_n 是一个常量表达式,用来指定数组的大小 数组创建的实例: //代码1 int a…...

【记录COCO数据集格式】实例分割的annotations.json的内部格式
在此记录一下实例分割coco的annotations.json的格式 annotations.json,整体是一个字典: { "info": {"description": null,"url": null, "version": null, "year": 2023, "contributor": null, "date_created…...

mac 关于获取手机信息 终端指令
iOS真机命令(自动化测试) 获取设备的的UDID idevice_id --list # 显示当前所连接设备的 udid instruments -s devices # 列出所有设备,包括真机、模拟器、mac ideviceinfo 可以在返回的数据中找到 udid idevice_id -l 苹果手机 safari打开网…...

ios消息推送例子
通过Apple推送服务,将消息发送给特定的ios客户端,这是服务器端实例代码。需要客户端的voip key值,以及相应的客户端回调接口,支持ios9.0以上版本。 下载地址:https://download.csdn.net/download/m0_37567738/8821559…...
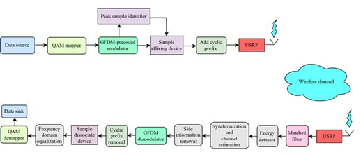
LabVIEW开发最小化5G系统测试平台
LabVIEW开发最小化5G系统测试平台 由于具有大量存储能力和数据的应用程序的智能手机的激增,当前一代产品被迫提高其吞吐效率。正交频分复用由于其卓越的品质,如单抽头均衡和具有成本效益的实施,现在被广泛用作物理层技术。这些好处是以严格的…...

如何用输入函数为数组赋值
在编写程序时我们经常使用数组,而数组的大小可能是很大的但是我们并不需要为每个元素都自己赋值,我们可能会自定义输入数组元素个数,我们应该如何实现通过输入函数为数组赋值呢? 目录 第一种: 第二种: 第一…...

【Python COM】Word 自动纵向合并相同内容单元格
使用场景 docxtempl 库不支持动态纵向合并单元格,所以写了这段代码用来曲线救国。 使用方法 需要纵向合并的单元格加上在文本末尾加上“【纵向合并】”,然后调用此函数,就会自动纵向合并相同内容的单元格。 代码 需要安装 pywin32 库。 …...

maven 环境变量的配置
1、安装好maven /home/sunyuhua/dev/apache-maven-3.9.32、编辑环境变量 vi /etc/profile.d/maven.shexport MAVEN_HOME/home/sunyuhua/dev/apache-maven-3.9.3 export PATH$PATH:$MAVEN_HOME/bin3、执行source source /etc/profile4、检验 mvn -version5、附注:…...

flutter-设置开屏页 解决开屏白屏问题
flutter_native_splash 当您的应用程序打开时,本机应用程序会短暂加载 Flutter。默认情况下,在此期间,本机应用程序会显示白色启动屏幕。该包自动生成 iOS、Android 和 Web 本机代码,用于自定义本机启动画面背景颜色和启动图像。支…...
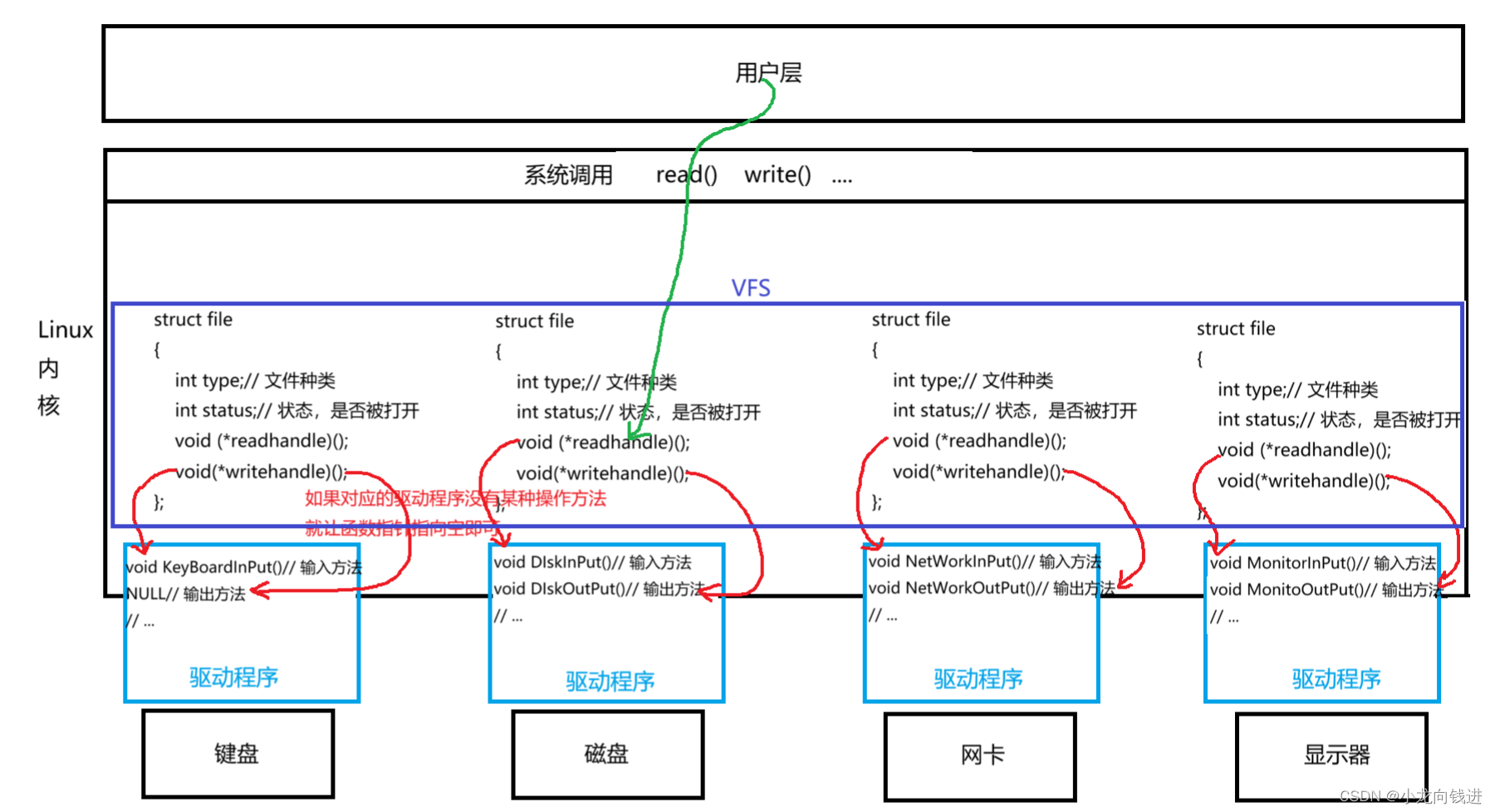
简单理解Linux中的一切皆文件
一款操作系统要管理各种各样不同的硬件,因为硬件的不同所以它们使用的文件系统也不同。但是按道理来说,文件系统的不同对于用户来说可不是一件好事,操作不同的硬件就要使用不同的方法。 但是Linux有一切皆文件。 简单来说,Linux…...
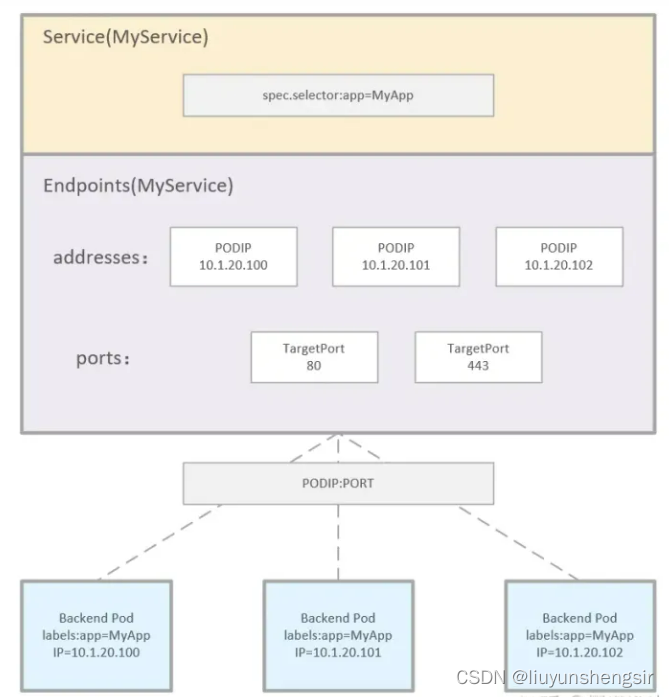
Kubernetes的endpoint
简介 Kubernetes的endpoint(终结点)是用于将服务绑定到集群中其他组件的网络地址。Endpoint为服务提供了一个稳定的虚拟IP地址,它会负责将流量从Service路由到后端Pod。 下面是使用Kubernetes的endpoint的详细步骤: 创建一个Se…...

第四章,向量组,2-矩阵等价与向量组等价的关系
第四章,向量组,2-矩阵等价与向量组等价的关系 矩阵乘法与线性表示矩阵等价与向量组等价 玩转线性代数(23)线性组合与线性表示的应用的笔记,相关证明以及例子见原文 矩阵乘法与线性表示 设有 A m ∗ n B n ∗ l C m ∗ l A_{m*n}B_{n*l}C_{m…...
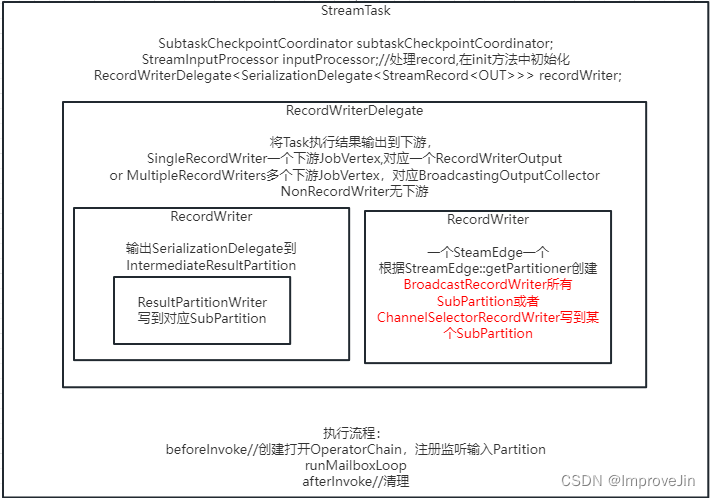
Flink源码之StreamTask启动流程
每个ExecutionVertex分配Slot后,JobMaster就会向Slot所在的TaskExecutor提交RPC请求执行Task,接口为TaskExecutorGateway::submitTask CompletableFuture<Acknowledge> submitTask(TaskDeploymentDescriptor tdd, JobMasterId jobMasterId, RpcTi…...
)
【BASH】回顾与知识点梳理(三十)
【BASH】回顾与知识点梳理 三十 三十. 进程的观察30.1 ps :将某个时间点的进程运作情况撷取下来仅观察自己的 bash 相关进程: ps -l观察系统所有进程: ps aux 30.2 top:动态观察进程的变化30.3 pstree 该系列目录 --> 【BASH】…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...

开疆智能Ethernet/IP转Modbus网关连接斯巴拓压力传感器配置案例
本案例是将ModbusRTU协议的压力传感器数据上传到欧姆龙PLC,由于PLC采用的是Ethernet/IP通讯协议,两者无法直接进行数据采集。故使用开疆智能研发的Ethernet转Modbus网关进行数据转换。 配置过程 首先我们开始配置Ethernet/IP主站(如罗克韦尔…...
