论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读
论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读
- Background
- Introduciton
- Problem Statement
- Methodology
- 总结
今天带来的是由微软Edward Hu等人完成并发表在ICLR 2022上的论文《LoRA: Low-Rank Adaptation of Large Language Models》,论文提出了大模型 tuning 框架 LoRA (Low-Rank Adaptation)。
论文地址:https://openreview.net/pdf?id=nZeVKeeFYf9
附录下载地址:https://openreview.net/attachment?id=nZeVKeeFYf9&name=supplementary_material
代码地址:https://github.com/microsoft/LoRA
Background
一些术语介绍:
· Intrinsic Dimension(本征维度):An objective function’s intrinsic dimensionality describes the minimum dimension needed to solve the optimization problem it defines to some precision level. 是指在pre-trained LLM中,对于下游的tuning工作,实际上不需要对模型所有参数都进行更新,在保证某种精度(如90%)的要求下,可以只更新一部分就可以了(可称为 d 90 d_{90} d90)。
few-shot learning:少样本学习。借助于少样本学习,大模型在特定下游任务的训练过程中,只需要少数的特定任务数据就可以发挥不错的性能。
Prompt Engineering:提示工程。这是 LLM 在 NLP 应用中的特有应用,类似于特征工程,是一种需要专家背景知识,通过组织input的格式,风格等内容,使得输入内容对LLM能够具备更好的促进作用。
Adaptation:适应。也就是大模型对特定下游任务的tuning,使其能够在下游任务中性能更好。
Introduciton
本文提出的主要出发点在于 大模型 的训练模式,即先通过对 大量的 task-independent 语料的预训练,然后再在特定任务上进行精调 fine-tuning,使得模型能够在特定的下游任务中展现较好的表现。
这里就出现一个问题,大模型无论是在存储还是计算上,都是很大的,需要很大的算力和存储。Fine-tuning所有参数就会很费时费力。举例来说,GPT-3 175B总共包含175 billion个参数,也就是1750亿个,fine-tuning所有层,所有Transformer中的Q K V 和 output 矩阵加上 bias,可想而知是一个很大的开销。如何解决这个问题构成本文的 Motivation。
当然已经有诸多此类问题的解决方案。例如,Adapter Layer,也就是在Transformer中插入了两层Adapter Layer 来适应下游任务,只更新Adapter Layer 中的参数,原来的Transformer中的参数 不进行更新。这类模型的问题在于,Adapter Layer 和原来的大模型参数是从输入到输出上下夹在一起的(类似于汉堡),参数计算时必须从输入到输出一层一层进行。那么模型在推理的时候,就必然涉及到等上一层计算完才可以计算下一层,那么就带来了模型的延迟,影响模型体验。
作者提出了低秩矩阵乘法作为任意矩阵 W W W的 特定增量 Δ W \Delta W ΔW,通过只更新 Δ W \Delta W ΔW 的方式减小模型开销的同时,保住模型性能。
是的,模型就是这么“简单”,但是一方面模型的切入点非常犀利;另一方面模型性能不错且带来了巨大的 tuning 节省,让贫穷的学生党探索大模型时能够更自如一些;同时,本文的实验部分也非常充分(附录中),在不同benchmark中的表现都能够佐证LoRA模型的有效性。

Problem Statement
首先是问题形式化,对于fine-tuning,就是把预训练完成的所有参数checkpoint进行存储dump,在精调阶段,将所有参数初始化为dump出来的value,以此作为参数更新的起始点,完成模型优化。表示如下:
max Φ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ ( y t ∣ x , y < t ) ) (1) \max _{\Phi} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(P_{\Phi}\left(y_{t} \mid x, y_{<t}\right)\right) \tag{1} Φmax(x,y)∈Z∑t=1∑∣y∣log(PΦ(yt∣x,y<t))(1)
如上所示,通过对下游任务数据集 Z \mathcal{Z} Z 进行模型所有参数 Φ \Phi Φ 的更新。如果 Φ {\Phi} Φ 很大,那么fine-tuning 就会很麻烦。
对此,作者提出了只更新 task-specific 的 新引入的 少量的参数 Δ Φ = Δ Φ ( Θ ) \Delta \Phi = \Delta \Phi(\Theta) ΔΦ=ΔΦ(Θ),完成模型的tuning。这里 Θ \Theta Θ 是新参数,而且维度相比较于原LLM模型很小( ∣ Θ ∣ ≪ ∣ Φ 0 ∣ |\Theta| \ll |\Phi_{0}| ∣Θ∣≪∣Φ0∣。作者指出,LoRA能够将需要更新的参数数量缩小到万分之一的地步。
max Θ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( p Φ 0 + Δ Φ ( Θ ) ( y t ∣ x , y < t ) ) (2) \max _{\Theta} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(p_{\Phi_{0}+\Delta \Phi(\Theta)}\left(y_{t} \mid x, y_{<t}\right)\right) \tag{2} Θmax(x,y)∈Z∑t=1∑∣y∣log(pΦ0+ΔΦ(Θ)(yt∣x,y<t))(2)
Methodology
LoRA的具体设计实际上用两句话可以完成概括,(1)引入低秩矩阵进行 Δ W \Delta W ΔW 的计算;(2)选择哪些矩阵进行引入。
Δ W \Delta W ΔW 的选择
对于 Δ W \Delta W ΔW 的计算,如下所示:
h = W 0 x + Δ W x = W 0 x + B A x (3) h=W_{0} x+\Delta W x=W_{0} x+B A x \tag{3} h=W0x+ΔWx=W0x+BAx(3)
即,针对Transformer中的矩阵,加入一个 B ⋅ A B \cdot A B⋅A 的操作,其中, B B B 和 A A A 共享的那个维度是 r r r,远小于 输入维度( x x x 的维度)和 输出维度 ( h h h 的维度)。
W W W的选择
Transformer中的几个矩阵可以分为四类,这里分别表示为Q/K/V/O,分别对应到query/key/value/output。作者在附录中加入了对矩阵的选择(所有可训练参数总数18M, 18 M / 175 B ≈ 1 / 10 K 18M/175B \approx 1/10K 18M/175B≈1/10K),可以看到对QKVO所有矩阵都进行更新,性能最佳。但是在文中,作者普遍使用了只更新QV的方式,并说QV表现更好,这里不太明白。

总结
本文simple but effective,值得一看!
相关文章:

论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读
论文《LoRA: Low-Rank Adaptation of Large Language Models》阅读 BackgroundIntroducitonProblem StatementMethodology Δ W \Delta W ΔW 的选择 W W W的选择 总结 今天带来的是由微软Edward Hu等人完成并发表在ICLR 2022上的论文《LoRA: Low-Rank Adaptation of Large Lan…...

MySQL数据类型篇
数值类型 类型有符号(SIGNED)取值范围无符号(UNSIGNED)取值范围大小描述TINYINT(-128,127)(0,255)1byte小整数值SMALLINT(-32768,32767)(0,65535)2bytes大整数值INT/INTEGER(-2147483648,2147483647)(0,429…...

Eureka注册中心
全部流程 注册服务中心 添加maven依赖 <!--引用注册中心--> <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId> </dependency> 配置Eureka 因为自…...

代码随想录算法训练营第53天|动态规划part14
8.19周六 1143.最长公共子序列 1035.不相交的线 53. 最大子序和 动态规划 详细布置 1143.最长公共子序列 题目:两个字符串,问最长的公共子序列多长(不连续) 题解: 1、dp[i][j]:长度为[0, i - 1]的字…...
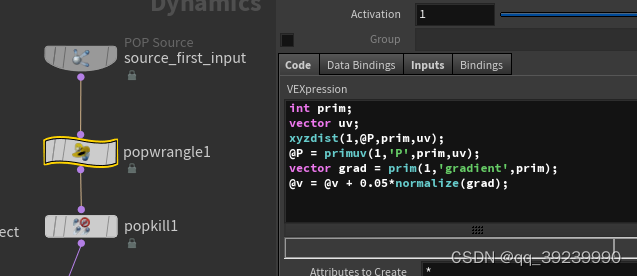
houdini xyzdist primuv 实现按路径走
2. meause distance v 0; add popforce...

Asrock-Z690-PG-Reptide i5-13600kf电脑 Hackintosh 黑苹果引导文件
硬件配置(需要下载请百度搜索:黑果魏叔) 硬件型号驱动情况主板 Asrock Z690 PG Reptide 处理器i5-13600kf RaptorLake (Undervolted)已驱动内存2x16Gb DDR4 3600 ADATA XPG已驱动硬盘1Tb Netac NV7000 NVME M2 (PCI-e 4.0)已驱动显卡Radeon …...
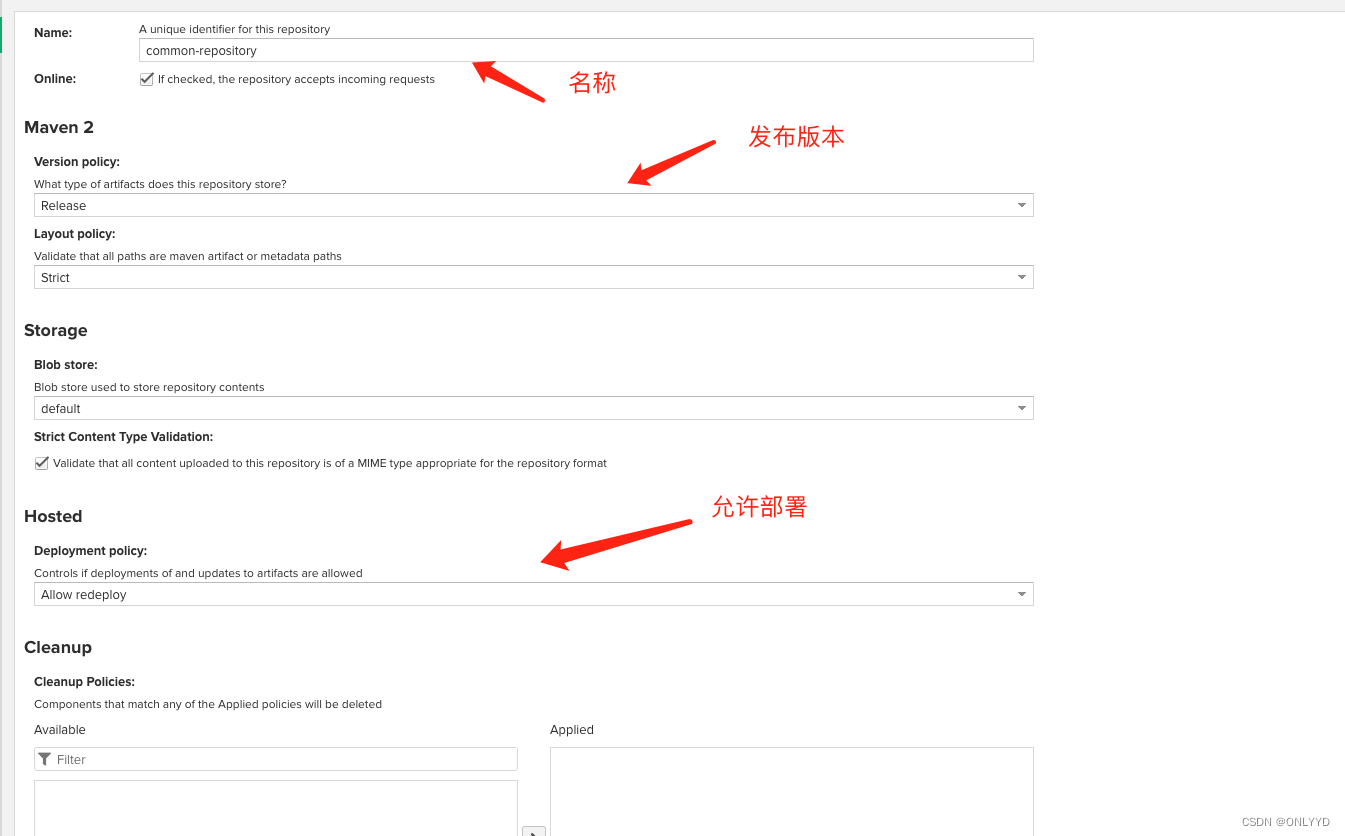
linux 搭建 nexus maven私服
目录 环境: 下载 访问百度网盘链接 官网下载 部署 : 进入目录,创建文件夹,进入文件夹 将安装包放入nexus文件夹,并解压编辑 启动 nexus,并查看状态.编辑 更改 nexus 端口为7020,并重新启动,访问虚拟机7020…...

MySQL中按月统计并逐月累加统计值的几种写法
有时候,我们可能有这样的场景,需要将销量按月统计,并且按月逐月累加。写惯了GROUP BY,按月统计倒是小case,但是逐月累加实现起来,要稍微麻烦一点。下面就整理几种写法,以备不时之需。 本月第一天 -- 本月第一天 SELE…...
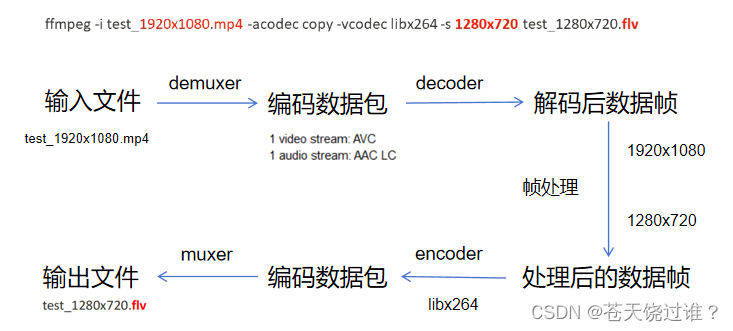
音视频 FFmpeg音视频处理流程
ffmpeg -i test_1920x1080.mp4 -acodec copy -vcodec libx264 -s 1280x720 test_1280x720.flv推荐一个零声学院项目课,个人觉得老师讲得不错,分享给大家: 零声白金学习卡(含基础架构/高性能存储/golang云原生/音视频/Linux内核&am…...

Linux网络编程:多进程 多线程_并发服务器
文章目录: 一:wrap常用函数封装 wrap.h wrap.c server.c client.c 二:多进程process并发服务器 实现思路 server.c服务器 client.c客户端 三:多线程thread并发服务器 实现思路 server.c服务器 client.c客户端 一&am…...
解决:(error) ERR unknown command shutdow,with args beginning with
目录 一、遇到问题 二、出现问题的原因 三、解决办法 一、遇到问题 要解决连接redis闪退的问题,按照许多的方式去进行都没有成功,在尝试使用了以下的命名去尝试时候,发现了这个问题。 二、出现问题的原因 这是一个粗心大意导致的错误&am…...

《TCP IP网络编程》第十八章
第 18 章 多线程服务器端的实现 18.1 理解线程的概念 线程背景: 第 10 章介绍了多进程服务端的实现方法。多进程模型与 select 和 epoll 相比的确有自身的优点,但同时也有问题。如前所述,创建(复制)进程的工作本身会…...

TCP编程流程
目录 1、主机字节序列和网络字节序列 2、套接字地址结构 3、IP地址转换函数 4、TCP协议编程: (1)服务器端: (2)客户端: 1、主机字节序列和网络字节序列 主机字节序列分为大端字节序和小端字节序 大端…...
)
CSDN编程题-每日一练(2023-08-19)
CSDN编程题-每日一练(2023-08-19) 一、题目名称:风险投资二、题目名称:幼稚班作业三、题目名称:韩信点兵一、题目名称:风险投资 时间限制:1000ms内存限制:256M 题目描述: 风险投资是一种感性和理性并存的投资方式,风险投资人一般会对请公允的第三方评估公司对投资对象…...
03_缓存双写一致性
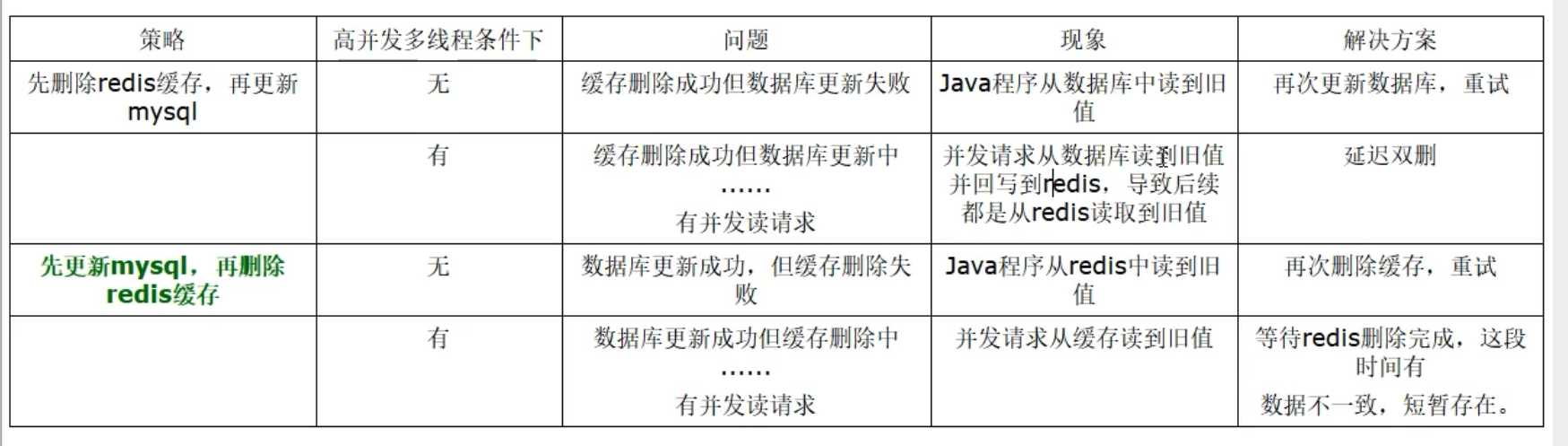
03——缓存双写一致性 一、缓存双写一致性 如果redis中有数据,需要和数据库中的值相同如果redis中无数据,数据库中的值要是最新值,且准备回写redis 缓存按照操作来分,可以分为两种: 只读缓存 读写缓存 同步直写操作…...

机器学习之数据集
目录 1、简介 2、可用数据集 3、scikit-learn数据集API 3.1、小数据集 3.2、大数据集 4、数据集使用 ⭐所属专栏:人工智能 文中提到的代码如有需要可以私信我发给你😊 1、简介 当谈论数据集时,通常是指在机器学习和数据分析中使用的一组…...

PyTorch Geometric基本教程
PyG官方文档 # Install torch geometric !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-geometricimport t…...

MAC 命令行启动tomcat的详细介绍
MAC 命令行启动tomcat MAC 命令行启动tomcat的详细介绍 一、修改授权 进入tomcat的bin目录,修改授权 1 2 3 ➜ bin pwd /Users/yp/Documents/workspace/apache-tomcat-7.0.68/bin ➜ bin sudo chmod 755 *.sh sudo为系统超级管理员权限.chmod 改变一个或多个文件的存取模…...
idea2023 springboot2.7.5+mybatisplus3.5.2+jsp 初学单表增删改查
创建项目 修改pom.xml 为2.7.5 引入mybatisplus 2.1 修改pom.xml <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.2</version></dependency><!--mysq…...
轻松搭建书店小程序
在现今数字化时代,拥有一个自己的小程序成为了许多企业和个人的追求。而对于书店经营者来说,拥有一个能够提供在线购书服务的小程序将有助于吸引更多的读者,并提升销售额。本文将为您介绍如何轻松搭建书店小程序,并将其成功上线。…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

mq安装新版-3.13.7的安装
一、下载包,上传到服务器 https://github.com/rabbitmq/rabbitmq-server/releases/download/v3.13.7/rabbitmq-server-generic-unix-3.13.7.tar.xz 二、 erlang直接安装 rpm -ivh erlang-26.2.4-1.el8.x86_64.rpm不需要配置环境变量,直接就安装了。 erl…...
