解决:(error) ERR unknown command shutdow,with args beginning with
目录
一、遇到问题
二、出现问题的原因
三、解决办法
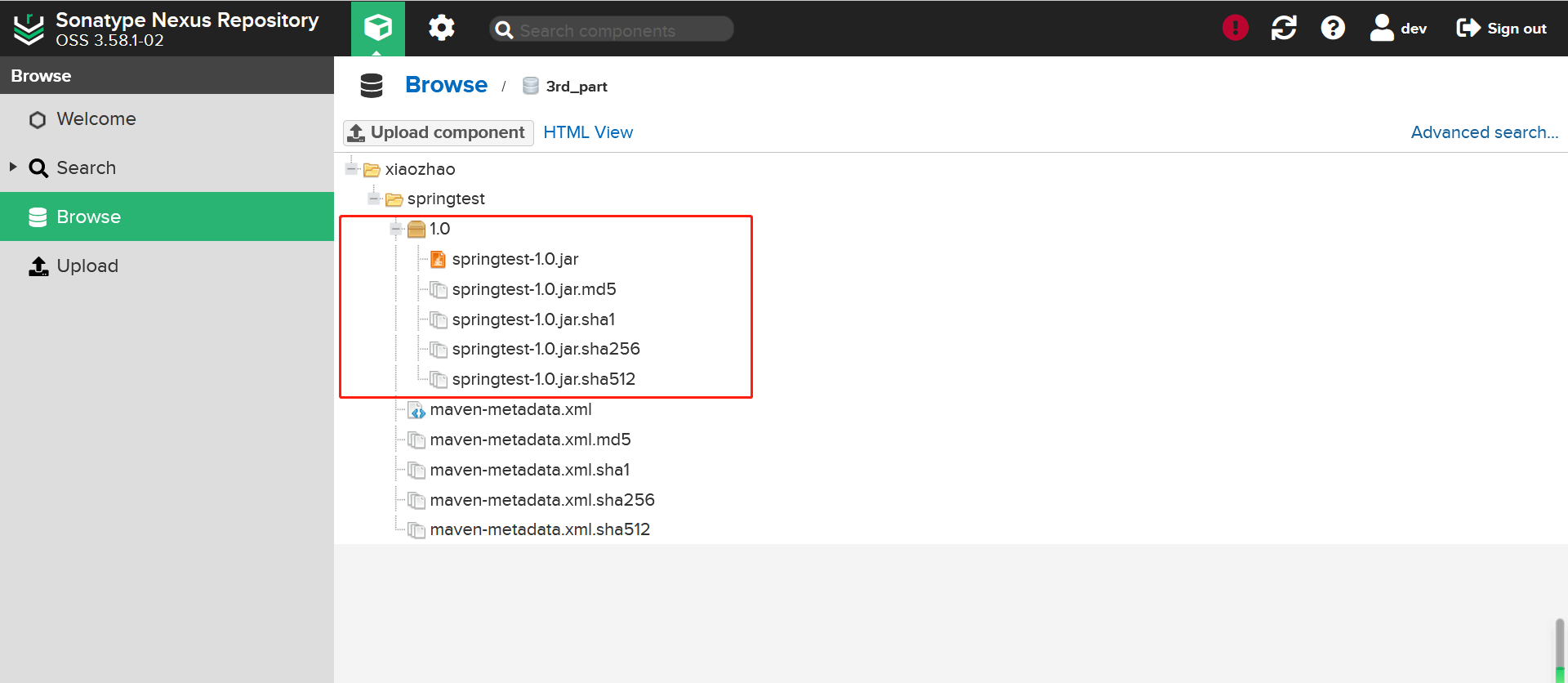
一、遇到问题
要解决连接redis闪退的问题,按照许多的方式去进行都没有成功,在尝试使用了以下的命名去尝试时候,发现了这个问题。
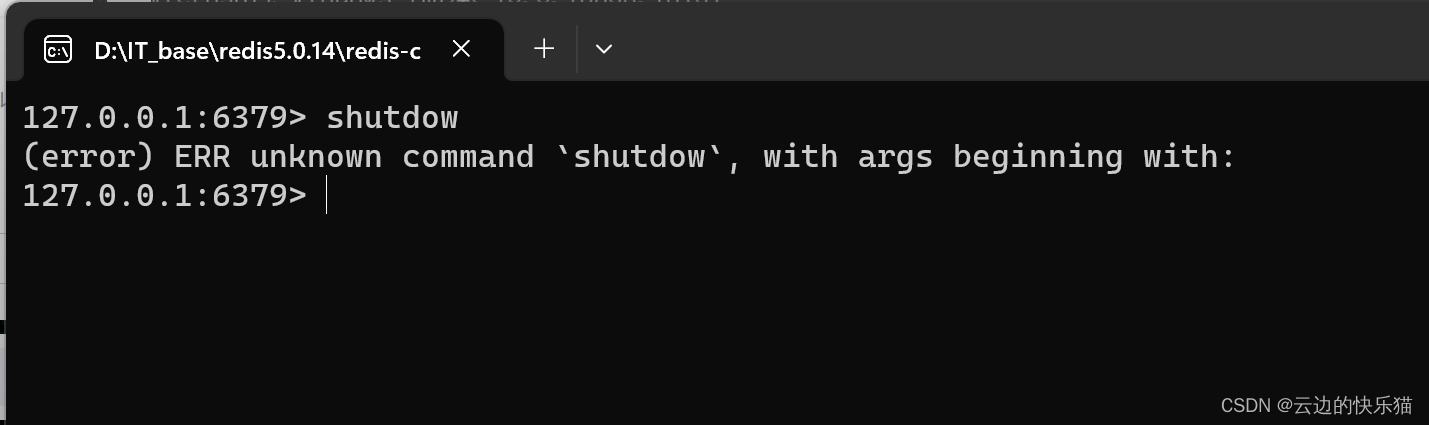
二、出现问题的原因
这是一个粗心大意导致的错误,检查自己输入的命令是否正确。
这个错误消息表明你尝试执行了一个 Redis 不识别的命令或命令参数,具体来说,是尝试执行了类似于
shutdow的命令。正常情况下,正确的命令应该是shutdown,这是用于关闭 Redis 服务器的命令。可能的原因和解决方法如下:
拼写错误:你可能在输入命令时拼写错误,导致 Redis 无法识别命令。确保你输入的是正确的命令,例如
shutdown而不是shutdow。自定义命令:如果你在 Redis 中定义了自定义的命令或别名,可能会导致类似的错误。确保你使用了 Redis 原生的命令。
版本问题:不同版本的 Redis 可能会有不同的命令支持。如果你使用的是较旧的 Redis 版本,可能某些命令不被支持。升级到更新的版本可能会解决这个问题。
命令参数错误:如果你在命令后面添加了不正确的参数,也可能导致类似的错误。检查命令及其参数是否正确。
三、解决办法
输入正确的命令:shutdown
有什么问题都可以评论区留言,看见都会回复的
点赞收藏评论,当然也可以点击文章底部的红包或者👇订阅付费文章创作支持一下了。抱拳了!
相关文章:

解决:(error) ERR unknown command shutdow,with args beginning with
目录 一、遇到问题 二、出现问题的原因 三、解决办法 一、遇到问题 要解决连接redis闪退的问题,按照许多的方式去进行都没有成功,在尝试使用了以下的命名去尝试时候,发现了这个问题。 二、出现问题的原因 这是一个粗心大意导致的错误&am…...

《TCP IP网络编程》第十八章
第 18 章 多线程服务器端的实现 18.1 理解线程的概念 线程背景: 第 10 章介绍了多进程服务端的实现方法。多进程模型与 select 和 epoll 相比的确有自身的优点,但同时也有问题。如前所述,创建(复制)进程的工作本身会…...

TCP编程流程
目录 1、主机字节序列和网络字节序列 2、套接字地址结构 3、IP地址转换函数 4、TCP协议编程: (1)服务器端: (2)客户端: 1、主机字节序列和网络字节序列 主机字节序列分为大端字节序和小端字节序 大端…...
)
CSDN编程题-每日一练(2023-08-19)
CSDN编程题-每日一练(2023-08-19) 一、题目名称:风险投资二、题目名称:幼稚班作业三、题目名称:韩信点兵一、题目名称:风险投资 时间限制:1000ms内存限制:256M 题目描述: 风险投资是一种感性和理性并存的投资方式,风险投资人一般会对请公允的第三方评估公司对投资对象…...
03_缓存双写一致性
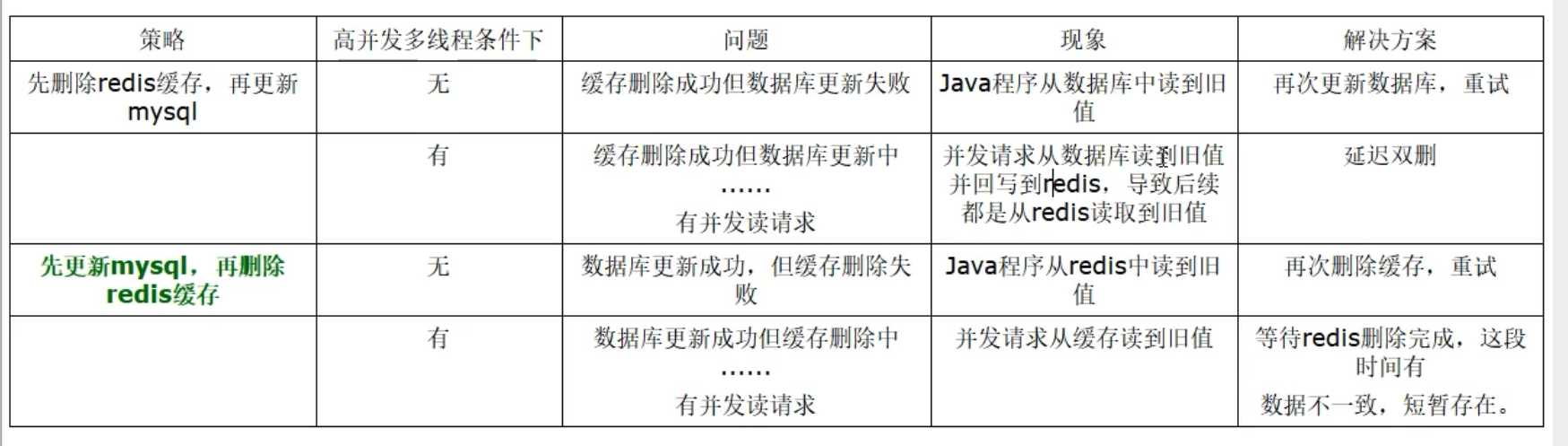
03——缓存双写一致性 一、缓存双写一致性 如果redis中有数据,需要和数据库中的值相同如果redis中无数据,数据库中的值要是最新值,且准备回写redis 缓存按照操作来分,可以分为两种: 只读缓存 读写缓存 同步直写操作…...

机器学习之数据集
目录 1、简介 2、可用数据集 3、scikit-learn数据集API 3.1、小数据集 3.2、大数据集 4、数据集使用 ⭐所属专栏:人工智能 文中提到的代码如有需要可以私信我发给你😊 1、简介 当谈论数据集时,通常是指在机器学习和数据分析中使用的一组…...

PyTorch Geometric基本教程
PyG官方文档 # Install torch geometric !pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.10.2cu102.html !pip install -q torch-geometricimport t…...

MAC 命令行启动tomcat的详细介绍
MAC 命令行启动tomcat MAC 命令行启动tomcat的详细介绍 一、修改授权 进入tomcat的bin目录,修改授权 1 2 3 ➜ bin pwd /Users/yp/Documents/workspace/apache-tomcat-7.0.68/bin ➜ bin sudo chmod 755 *.sh sudo为系统超级管理员权限.chmod 改变一个或多个文件的存取模…...
idea2023 springboot2.7.5+mybatisplus3.5.2+jsp 初学单表增删改查
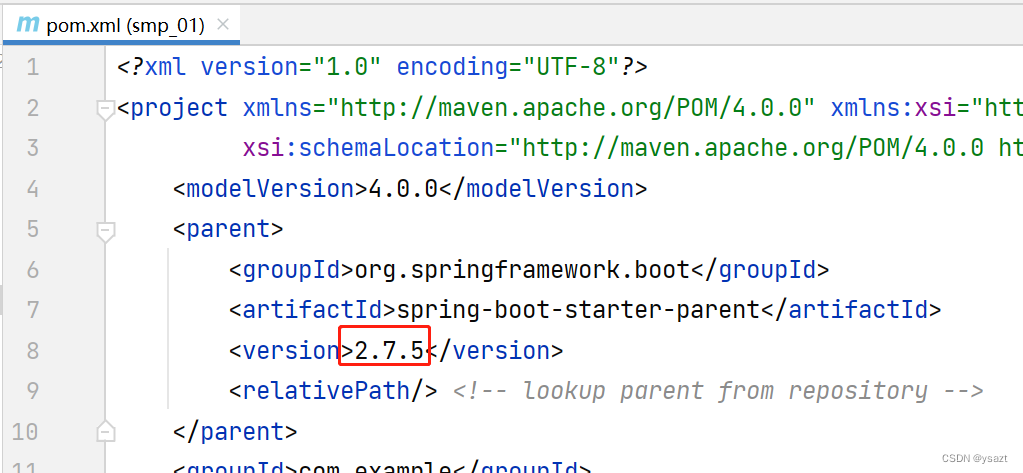
创建项目 修改pom.xml 为2.7.5 引入mybatisplus 2.1 修改pom.xml <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.2</version></dependency><!--mysq…...
轻松搭建书店小程序
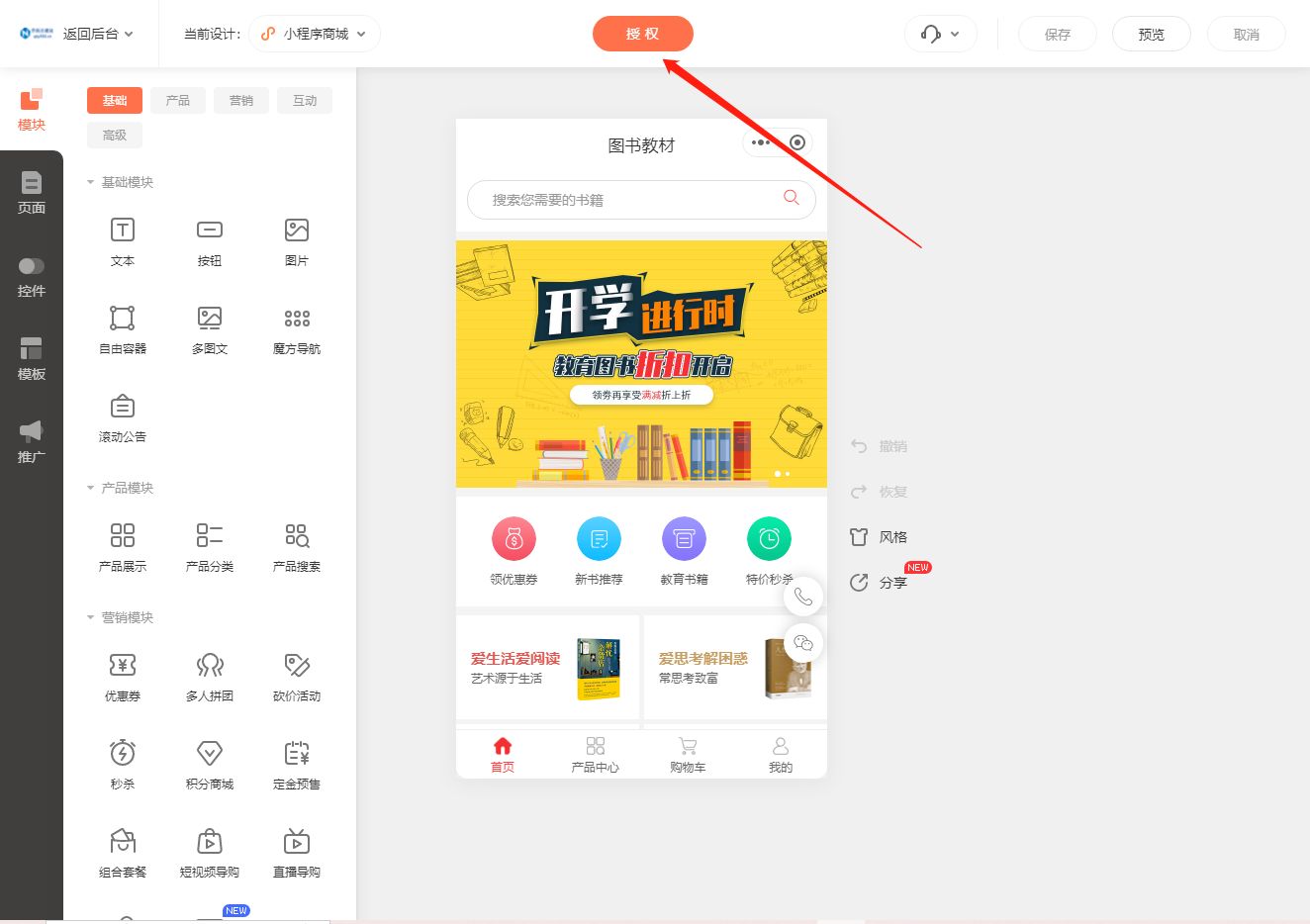
在现今数字化时代,拥有一个自己的小程序成为了许多企业和个人的追求。而对于书店经营者来说,拥有一个能够提供在线购书服务的小程序将有助于吸引更多的读者,并提升销售额。本文将为您介绍如何轻松搭建书店小程序,并将其成功上线。…...

Spark MLlib机器学习库(一)决策树和随机森林案例详解
Spark MLlib机器学习库(一)决策树和随机森林案例详解 1 决策树预测森林植被 1.1 Covtype数据集 数据集的下载地址: https://www.kaggle.com/datasets/uciml/forest-cover-type-dataset 该数据集记录了美国科罗拉多州不同地块的森林植被类型,每个样本…...
CI/CD入门(二)
CI/CD入门(二) 目录 CI/CD入门(二) 1、代码上线方案 1.1 早期手动部署代码1.2 合理化上线方案1.3 大型企业上线制度和流程1.4 php程序代码上线的具体方案1.5 Java程序代码上线的具体方案1.6 代码上线解决方案注意事项2、理解持续集成、持续交付、持续部署 2.1 持续集成2.2 持续…...
)
【BASH】回顾与知识点梳理(三十五)
【BASH】回顾与知识点梳理 三十五 三十五. 二十七至三十四章知识点总结及练习35.1 总结35.2 练习RAIDLVMsystemd 35.3 简答题 该系列目录 --> 【BASH】回顾与知识点梳理(目录) 三十五. 二十七至三十四章知识点总结及练习 35.1 总结 Quota 可公平的分…...
excel逻辑函数篇2
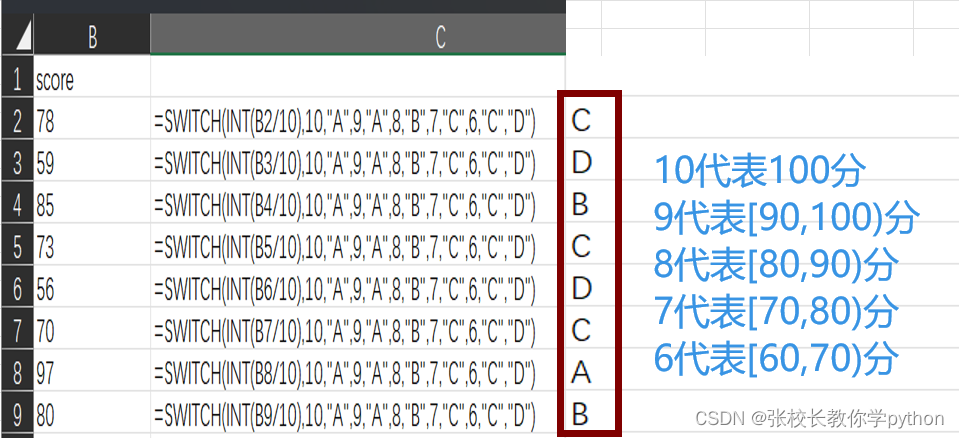
1、IF(logical_test,[value_if_true],[value_if_false]):判断是否满足某个条件,如果满足返回一个值,如果不满足则返回另一个值 if(条件,条件成立返回的值,条件不成立返回的值) 2、IFS(logical_test1,value_if_true1,…):检查是否…...

设计模式详解-解释器模式
类型:行为型模式 实现原理:实现了一个表达式接口,该接口使用标识来解释语言中的句子 作用:给定一个语言,定义它的文法表示,并定义一个解释器,这个解释器来解释。 主要解决:一些重…...

如何在React项目中动态插入HTML内容
React是一种流行的JavaScript库,用于构建用户界面。它提供了一种声明式的方法来创建可复用的组件,使得开发者能够更轻松地构建交互性的Web应用程序。在React中,我们通常使用JSX语法来描述组件的结构和行为。 在某些情况下,我们可…...
十六、Spring Cloud Sleuth 分布式请求链路追踪
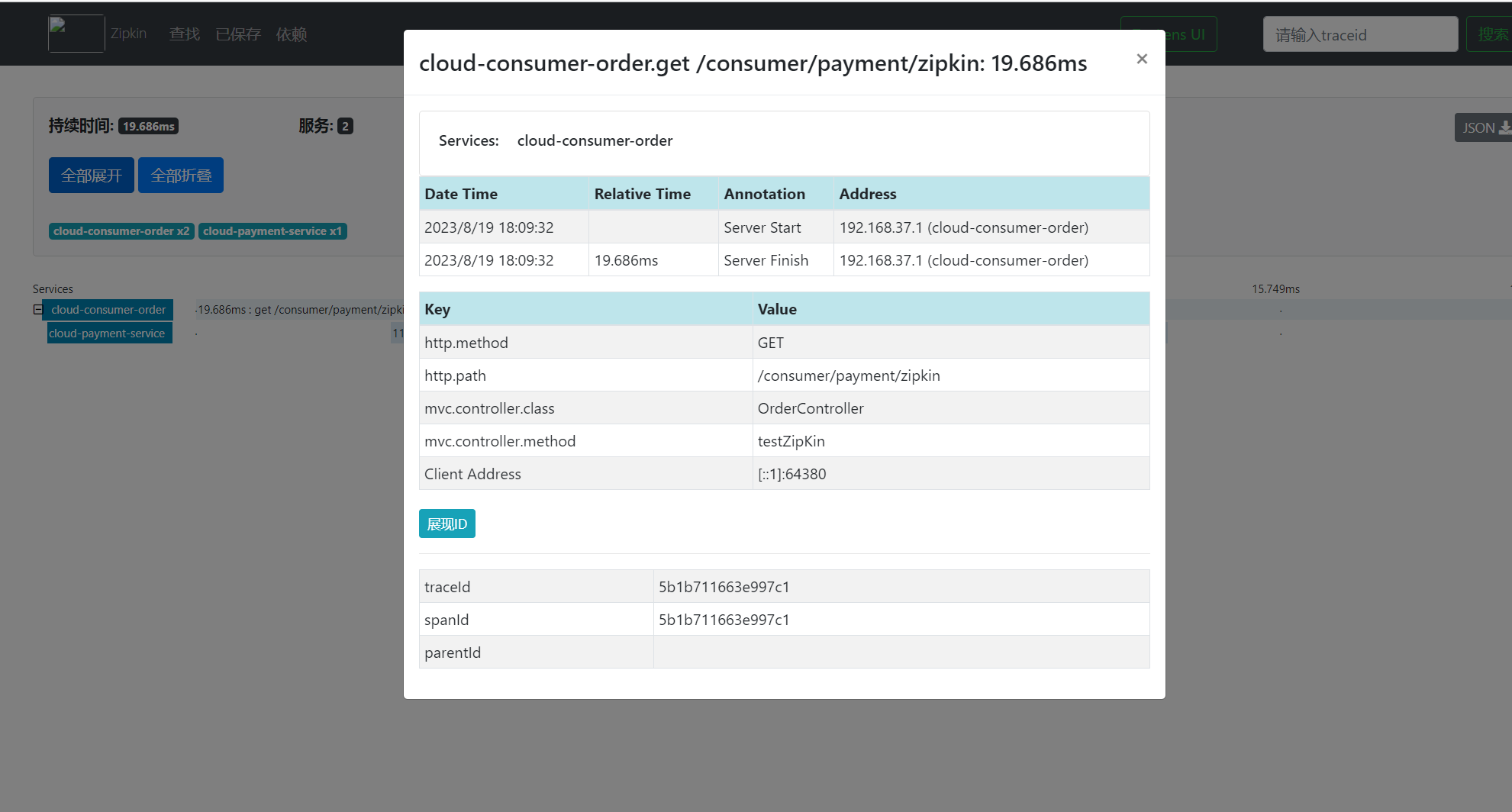
目录 一、概述1、为什么出出现这个技术?需要解决哪些问题2、是什么?3、解决 二、搭建链路监控步骤1、下载运行zipkin2、服务提供者3、服务调用者4、测试 一、概述 1、为什么出出现这个技术?需要解决哪些问题 2、是什么? 官网&am…...

ElasticSearch DSL语句(bool查询、算分控制、地理查询、排序、分页、高亮等)
文章目录 DSL 查询种类DSL query 基本语法1、全文检索2、精确查询3、地理查询4、function score (算分控制)5、bool 查询 搜索结果处理1、排序2、分页3、高亮 RestClient操作 DSL 查询种类 查询所有:查询所有数据,一般在测试时使…...
)
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(2,概率基本公式与事件独立)
文章目录 引言四、概率基本公式4.1 减法公式4.2 加法公式4.3 条件概率公式4.4 乘法公式 五、事件的独立性5.1 事件独立的定义5.1.1 两个事件的独立5.1.2 三个事件的独立 5.2 事件独立的性质 写在最后 引言 承接上文,继续介绍概率论与数理统计第一章的内容。 四、概…...

SpringBoot整合RabbitMQ,笔记整理
1创建生产者工程springboot-rabbitmq-produce 2.修改pom.xml文件 <!--父工程--> <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.0</version><r…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
