神经网络基础-神经网络补充概念-47-动量梯度下降法
概念
动量梯度下降法(Momentum Gradient Descent)是一种优化算法,用于加速梯度下降的收敛速度,特别是在存在高曲率、平原或局部最小值的情况下。动量法引入了一个称为“动量”(momentum)的概念,它模拟了物体在运动中积累的速度,使得参数更新更具有惯性,从而更平稳地更新参数并跳过一些不必要的波动。
基本原理和步骤
1初始化参数:初始化模型的参数。
2初始化速度:初始化速度为零向量。
3计算梯度:计算当前位置的梯度。
4更新速度:根据当前梯度和先前速度,计算新的速度。
velocity = beta * velocity + (1 - beta) * gradient其中,beta 是动量的超参数,通常取值在0到1之间。
5更新参数:根据新的速度,更新模型的参数。
6重复迭代:重复执行步骤 3 到 5,直到达到预定的迭代次数(epochs)或收敛条件。
动量梯度下降法可以帮助算法跳过较为平坦的区域,加速收敛,并减少参数在局部最小值附近的震荡。这在深度学习中特别有用,因为神经网络的参数空间通常很复杂。
代码实现
import numpy as np
import matplotlib.pyplot as plt# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]# 初始化参数
theta = np.random.randn(2, 1)# 学习率
learning_rate = 0.01# 动量参数
beta = 0.9
velocity = np.zeros_like(theta)# 迭代次数
n_iterations = 1000# 动量梯度下降
for iteration in range(n_iterations):gradients = 2 / 100 * X_b.T.dot(X_b.dot(theta) - y)velocity = beta * velocity + (1 - beta) * gradientstheta = theta - learning_rate * velocity# 绘制数据和拟合直线
plt.scatter(X, y)
plt.plot(X, X_b.dot(theta), color='red')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression with Momentum Gradient Descent')
plt.show()print("Intercept (theta0):", theta[0][0])
print("Slope (theta1):", theta[1][0])相关文章:

神经网络基础-神经网络补充概念-47-动量梯度下降法
概念 动量梯度下降法(Momentum Gradient Descent)是一种优化算法,用于加速梯度下降的收敛速度,特别是在存在高曲率、平原或局部最小值的情况下。动量法引入了一个称为“动量”(momentum)的概念,…...
 补充知识、线程池浅谈、数量谈、总结)
C++11并发与多线程笔记(13) 补充知识、线程池浅谈、数量谈、总结
C11并发与多线程笔记(13) 补充知识、线程池浅谈、数量谈、总结 1、补充一些知识点1.1 虚假唤醒:1.2 atomic 2、浅谈线程池:3、线程创建数量谈: 1、补充一些知识点 1.1 虚假唤醒: notify_one或者notify_al…...
python高级基础
文章目录 python高级基础闭包修饰器单例模式跟工厂模式工厂模式单例模式 多线程多进程创建websocket服务端手写客户端 python高级基础 闭包 简单解释一下闭包就是可以在内部访问外部函数的变量,因为如果声明全局变量,那在后面就有可能会修改 在闭包中的…...
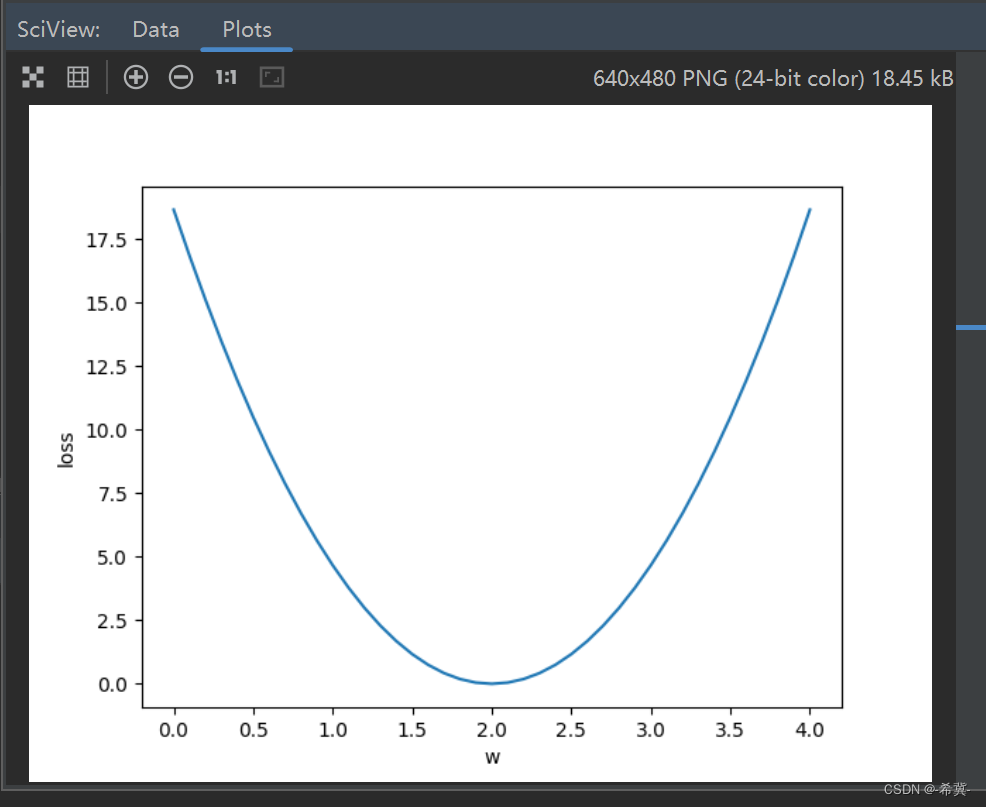
使用线性回归模型优化权重:探索数据拟合的基础
文章目录 前言一、示例代码二、示例代码解读1.线性回归模型2.MSE损失函数3.优化过程4.结果解读 总结 前言 在机器学习和数据科学中,线性回归是一种常见而重要的方法。本文将以一个简单的代码示例为基础,介绍线性回归的基本原理和应用。将使用Python和Nu…...

亿级短视频,如何架构?
说在前面 在尼恩的(50)读者社群中,经常指导大家面试架构,拿高端offer。 前几天,指导一个年薪100W小伙伴,拿到字节面试邀请。 遇到一个 非常、非常高频的一个面试题,但是很不好回答࿰…...
jenkins pipeline方式一键部署github项目
上篇:jenkins一键部署github项目 该篇使用jenkins pipeline-script一键部署,且介绍pipeline-scm jenkins环境配置 前言:按照上篇创建pipeline任务,结果报mvn,jdk环境不存在,就很疑惑,然后配置全…...
Vue 项目搭建
环境配置 1. 安装node.js 官网:nodejs(推荐 v10 以上) 官网:npm 是什么? 由于vue的安装与创建依赖node.js(JavaScript的运行环境)里的npm(包管理和分发工具)ÿ…...
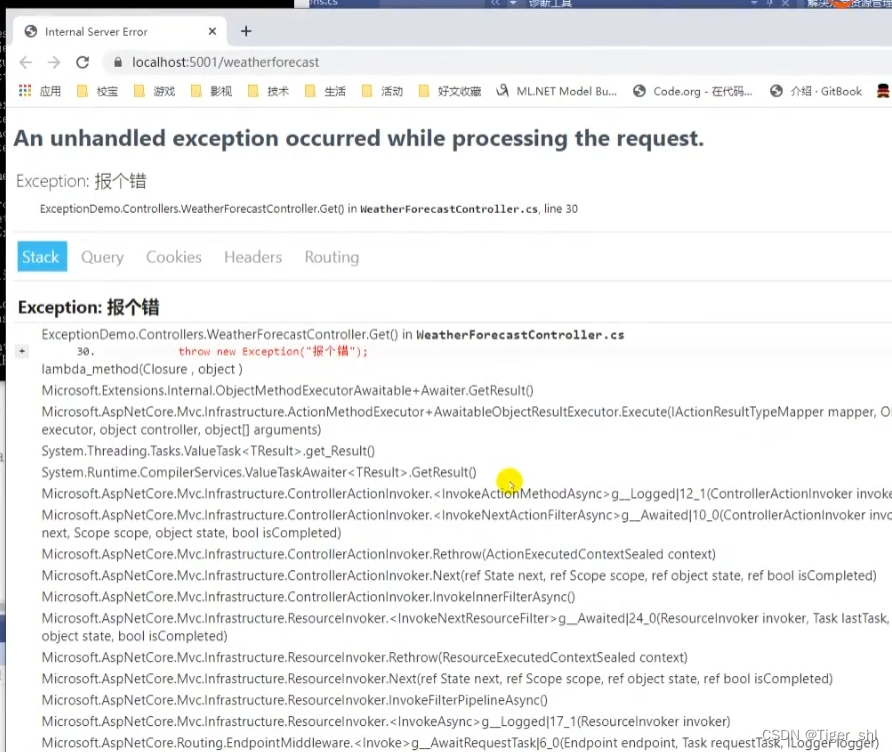
【NetCore】09-中间件
文章目录 中间件:掌控请求处理过程的关键1. 中间件1.1 中间件工作原理1.2 中间件核心对象 2.异常处理中间件:区分真异常和逻辑异常2.1 处理异常的方式2.1.1 日常错误处理--定义错误页的方法2.1.2 使用代理方法处理异常2.1.3 异常过滤器 IExceptionFilter2.1.4 特性过…...
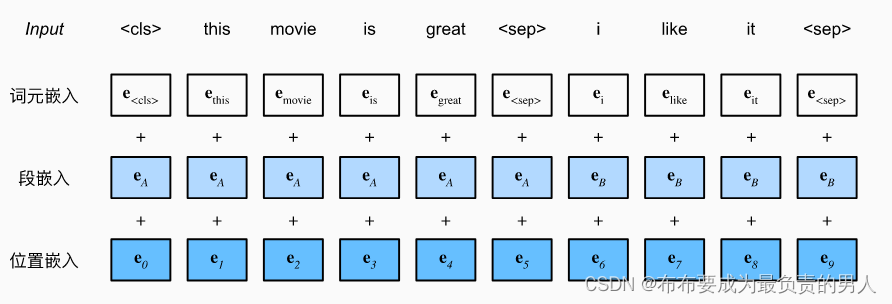
机器学习深度学习——BERT(来自transformer的双向编码器表示)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——transformer(机器翻译的再实现) 📚订阅专栏:机器学习&am…...
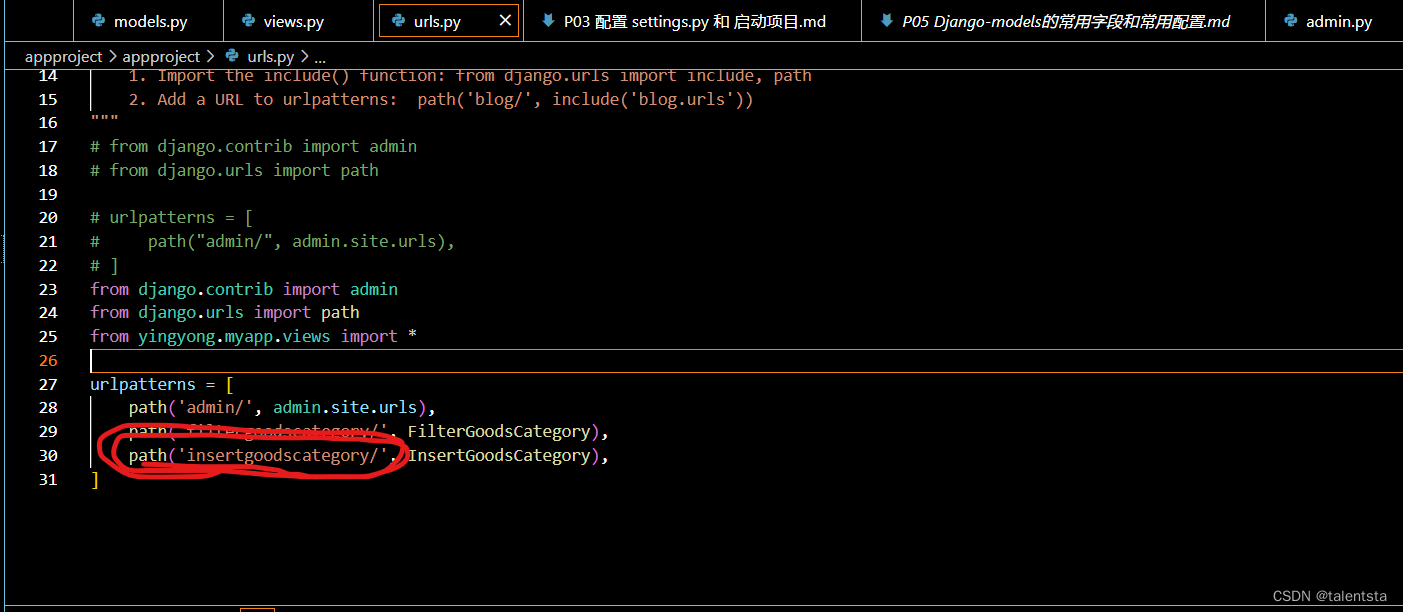
Datawhale Django后端开发入门 Vscode TASK02 Admin管理员、外键的使用
一.Admin管理员的使用 1、启动django服务 使用创建管理员之前,一定要先启动django服务,虽然TASK01和TASK02是分开的,但是进行第二个流程的时候记得先启动django服务,注意此时是在你的项目文件夹下启动的,时刻注意要执…...
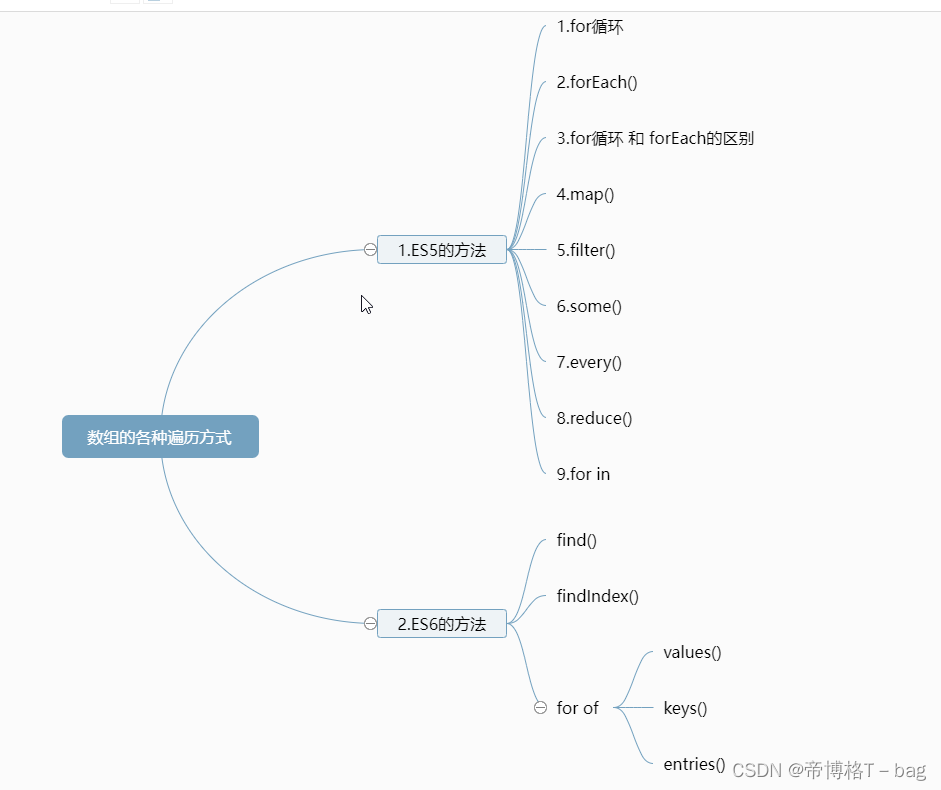
【ES5和ES6】数组遍历的各种方法集合
一、ES5的方法 1.for循环 let arr [1, 2, 3] for (let i 0; i < arr.length; i) {console.log(arr[i]) } // 1 // 2 // 32.forEach() 特点: 没有返回值,只是针对每个元素调用func三个参数:item, index, arr ;当前项&#…...

学科在线教育元宇宙VR虚拟仿真平台落实更高质量的交互学习
为推动教育数字化,建设全民终身学习的学习型社会、学习型大国,元宇宙企业深圳华锐视点深度融合VR虚拟现实、数字孪生、云计算和三维建模等技术,搭建教育元宇宙平台,为学生提供更加沉浸式的学习体验,提高学习效果和兴趣…...
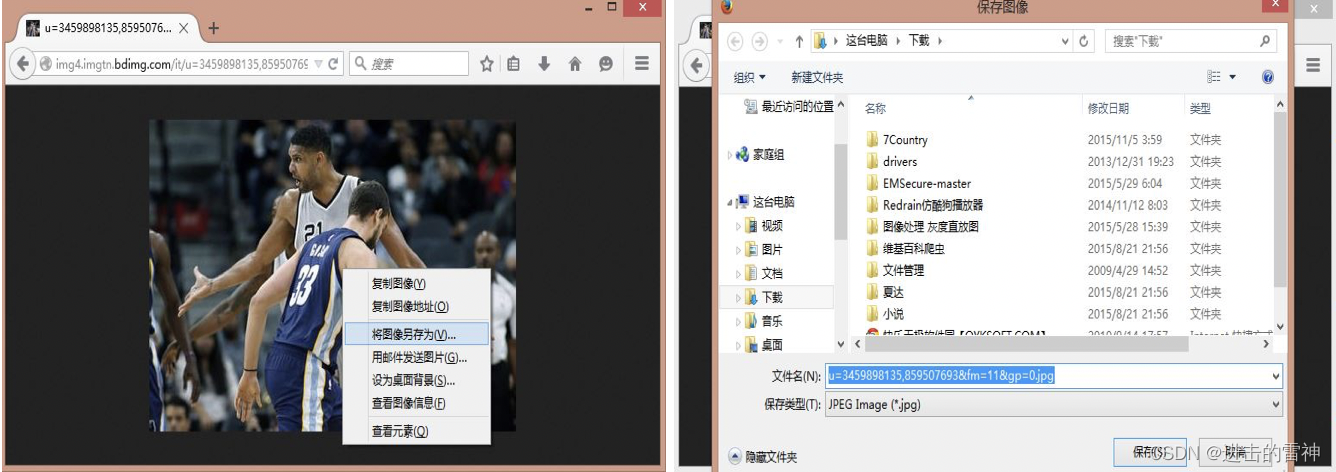
[python爬虫] 爬取图片无法打开或已损坏的简单探讨
本文主要针对python使用urlretrieve或urlopen下载百度、搜狗、googto(谷歌镜像)等图片时,出现"无法打开图片或已损坏"的问题,作者对它进行简单的探讨。同时,作者将进一步帮你巩固selenium自动化操作和urllib…...

vue项目预览pdf功能(解决动态文字无法显示的问题)
最近,因为公司项目需要预览pdf的功能,开始的时候找了市面上的一些pdf插件,都能用,但是,后面因为pdf变成了需要根据内容进行变化的,然后,就出现了需要动态生成的文字不显示了。换了好多好多的插件…...

vue3 样式穿透:deep不生效
初学vue3,今天需要修改el-input组件的属性(去掉border和文字居右) 网上搜了一下,大致都是采用:deep 样式穿透来修改el-input的属性 <div class"input-container"><el-input placeholder"请输入111&qu…...
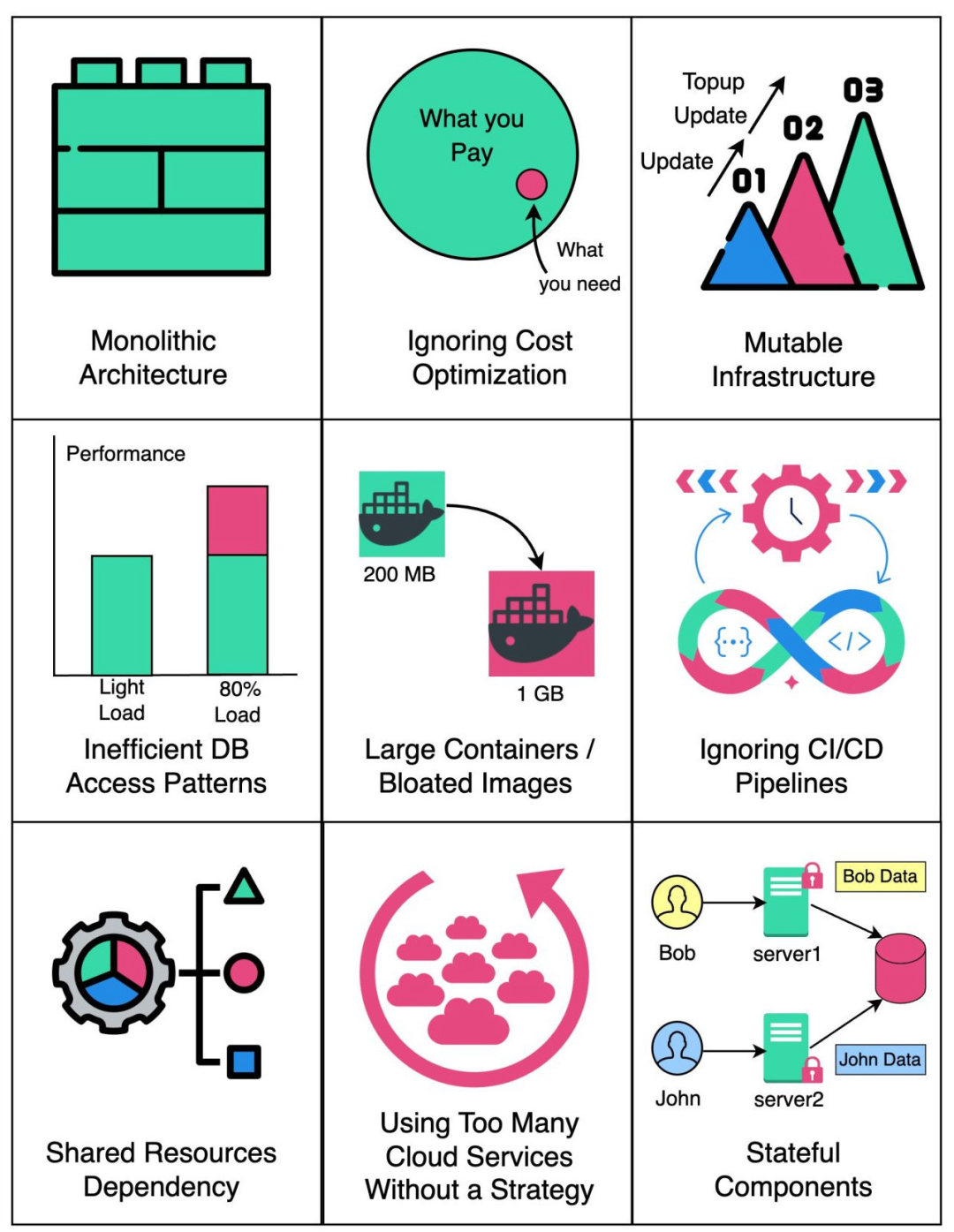
云原生反模式
通过了解这些反模式并遵循云原生最佳实践,您可以设计、构建和运营更加强大、可扩展和成本效益高的云原生应用程序。 1.单体架构:在云上运行一个大而紧密耦合的应用程序,妨碍了可扩展性和敏捷性。2.忽略成本优化:云服务可能昂贵&am…...
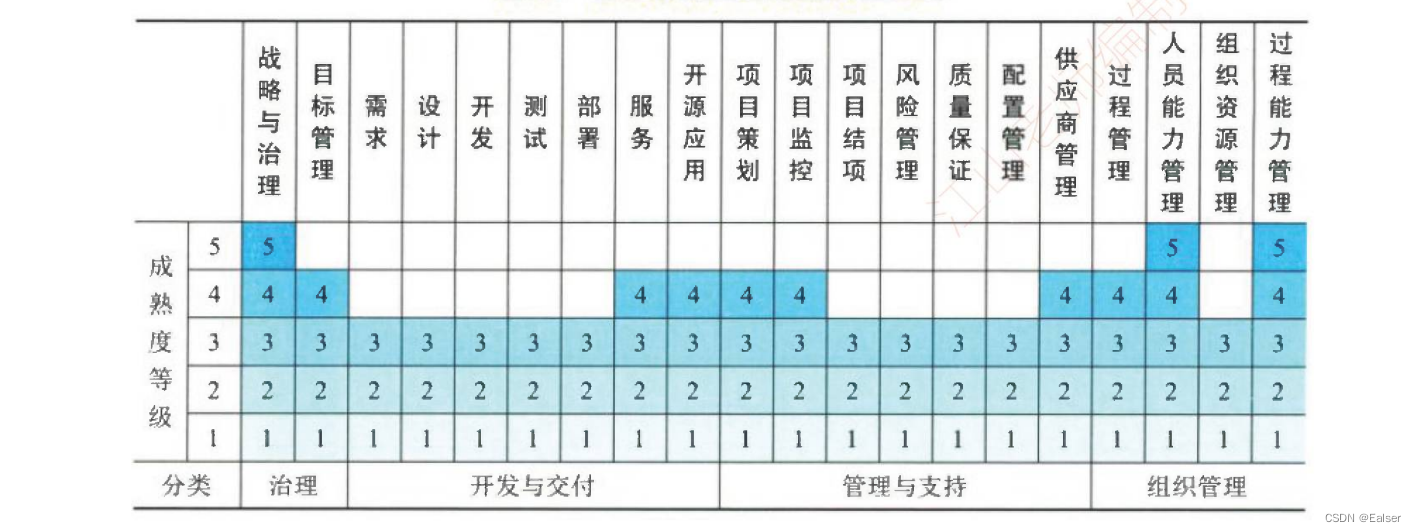
【2023年11月第四版教材】《第5章-信息系统工程(合集篇)》
《第5章-信息系统工程(合集篇)》 章节说明1 软件工程1.1 架构设计1.2 需求分析1.3 软件设计1.4 软件实现[补充第三版教材内容] 1.5 部署交付 2 数据工程2.1 数据建模2.2 数据标准化2.3 数据运维2.4 数据开发利用2.5 数据库安全 3 …...

【qiankun】微前端在项目中的具体使用
1、安装qiankun npm install qiankun --save2、主应用中注册和配置qiankun 在主应用的入口文件main.ts中,引入qiankun的注册方法: import { registerMicroApps, start } from qiankun;创建一个数组,用于配置子应用的相关信息。每个子应用都…...

云安全与多云环境管理:讨论在云计算和多云环境下如何保护数据、应用程序和基础设施的安全
随着云计算和多云环境的广泛应用,企业正面临着数据、应用程序和基础设施安全的新挑战。在这个数字化时代,保护敏感信息和业务运作的连续性变得尤为重要。本文将深入探讨在云计算和多云环境下如何有效地保护数据、应用程序和基础设施的安全。 章节一&…...
npm install ffi各种失败,换命令npm i ffi-napi成功
网上各种帖子安装ffi,基本上到了windows build tools这里会卡住。 使用命令npm install --global --production windows-build-tools 安装报错信息如下: PS E:\codes\nodejsPath\tcpTest> npm install --global --production windows-build-tools …...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
