当前位置： 首页 > news >正文

山西电力市场日前价格预测【2023-08-20】

news 2026/2/10 21:26:59

日前价格预测

预测明日（2023-08-20）山西电力市场全天平均日前电价为341.71元/MWh。其中，最高日前电价为367.66元/MWh，预计出现在20: 30。最低日前电价为318.47元/MWh，预计出现在04: 15。

价差方向预测

1： 实时价格 > 日前价格

0： 实时价格 = 日前价格

-1：实时价格 < 日前价格

注：价差代表的是原始出清价格的价差，并非最终结算价格的价差。

以上预测仅供学习参考，严禁用于商业用途。

昨日日前价格预测回顾

2023-08-19 全天96个点平均预测准确率96.43%，平均绝对偏差为12.66元/MWh。最大偏差为38.68元/MWh,出现在13:30。最小偏差为0.15元/MWh,出现在19:45 。

 价差方向预测回顾

蓝色柱状图表示：该时段预测价差方向与实际价差方向一致。

红色柱状图表示：该时段预测价差方向与实际价差方向相反。

2023-08-18 全天96个时段价差方向预测准确率：-19.6%     

注：价差方向预测准确率计算公式：

图片

D：价差方向预测值（1:实时>日前，0:实时=日前，-1:实时<日前）

P:  价格   

i： 时段

相关文章：

山西电力市场日前价格预测【2023-08-20】

日前价格预测 预测明日&#xff08;2023-08-20&#xff09;山西电力市场全天平均日前电价为341.71元/MWh。其中&#xff0c;最高日前电价为367.66元/MWh&#xff0c;预计出现在20: 30。最低日前电价为318.47元/MWh&#xff0c;预计出现在04: 15。 价差方向预测 1&#xff1a; 实…...

编程日记 2023/8/20 9:30:39

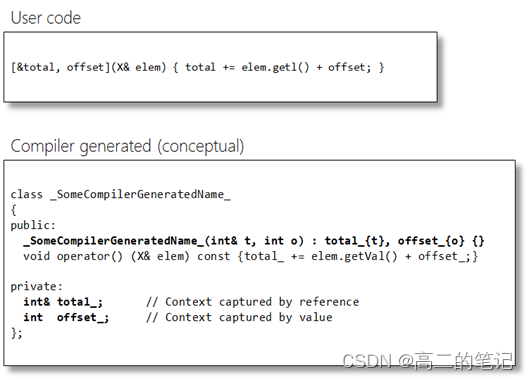
C++中function,bind,lambda

c11之前&#xff0c;STL中提供了bind1st以及bind2nd绑定器 首先来看一下他们如何使用&#xff1a; 如果我们要对vector中的元素排序&#xff0c;首先会想到sort&#xff0c;比如&#xff1a; void output(const vector<int> &vec) {for (auto v : vec) {cout <&l…...

编程日记 2023/8/20 9:29:37

跟着美团学设计模式（感处）

读了着篇文章之后发现真的是&#xff0c;你的思想&#xff0c;你的思维是真的比比你拥有什么技术要强的。 注 开闭原则 开闭原则&#xff08;Open-Closed Principle&#xff09;是面向对象设计中的基本原则之一&#xff0c;它的定义是&#xff1a;一个软件实体应该对扩展开放…...

编程日记 2023/8/20 9:28:36

2023/8/19 小红书 Java 后台开发面经

项目都做了些什么&#xff0c;怎么实现的用Redis实现了什么&#xff0c;Redis是单线程的吗&#xff0c;Redis是单线程的为什么快&#xff0c;IO多路复用模型具体实现&#xff0c;持久化怎么实现的为什么用Kafka&#xff0c;架构是什么样的&#xff0c;Broker、Topic、Partition…...

编程日记 2023/8/20 9:27:34

基于traccar快捷搭建gps轨迹应用

0. 环境 - win10 虚拟机ubuntu18 - i5 ubuntu22笔记本 - USB-GPS模块一台&#xff0c;比如华大北斗TAU1312-232板 - 双笔记本组网设备&#xff1a;路由器&#xff0c;使得win10笔记本ip&#xff1a;192.168.123.x&#xff0c;而i5笔记本IP是192.168.123.215。 - 安卓 手机 1.…...

编程日记 2023/8/20 9:26:31

【深度学习-图像识别】使用fastai对Caltech101数据集进行图像多分类（50行以内的代码就可达到很高准确率）

文章目录 前言fastai介绍数据集介绍 一、环境准备二、数据集处理1.数据目录结构2.导入依赖项2.读入数据3.模型构建3.1 寻找合适的学习率3.2 模型调优 4.模型保存与应用 总结人工智能-图像识别 系列文章目录 前言 fastai介绍 fastai 是一个深度学习库&#xff0c;它为从业人员…...

编程日记 2023/8/20 9:25:30

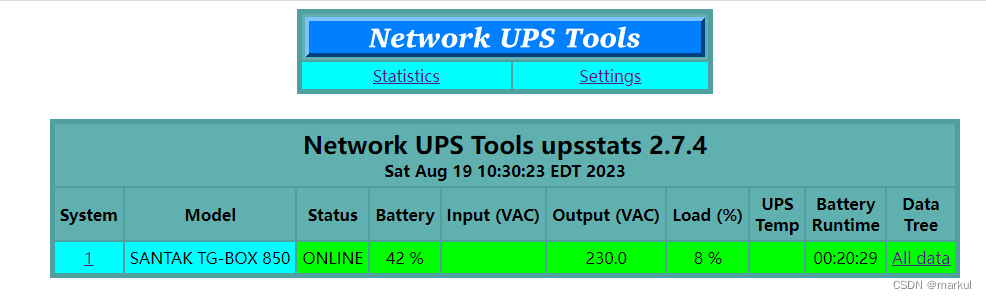
Debian10: 安装nut服务器(UPS)

UPS说明&#xff1a; UPS的作用就不必讲了&#xff0c;我选择是SANTAKTGBOX-850&#xff0c;规格为 850VA/510W&#xff0c;可以满足所需&#xff0c;关键是Debian10自带了驱动可以支持&#xff0c;免去安装驱动&#xff0c;将UPS通过USB线连接服务器即可&#xff0c;如下图所示…...

编程日记 2023/8/20 9:24:28

神经网络基础-神经网络补充概念-47-动量梯度下降法

概念 动量梯度下降法&#xff08;Momentum Gradient Descent&#xff09;是一种优化算法&#xff0c;用于加速梯度下降的收敛速度&#xff0c;特别是在存在高曲率、平原或局部最小值的情况下。动量法引入了一个称为“动量”&#xff08;momentum&#xff09;的概念&#xff0c…...

编程日记 2023/8/20 9:23:27

C++11并发与多线程笔记（13） 补充知识、线程池浅谈、数量谈、总结

C11并发与多线程笔记&#xff08;13&#xff09; 补充知识、线程池浅谈、数量谈、总结 1、补充一些知识点1.1 虚假唤醒&#xff1a;1.2 atomic 2、浅谈线程池&#xff1a;3、线程创建数量谈&#xff1a; 1、补充一些知识点 1.1 虚假唤醒&#xff1a; notify_one或者notify_al…...

编程日记 2023/8/20 9:22:25

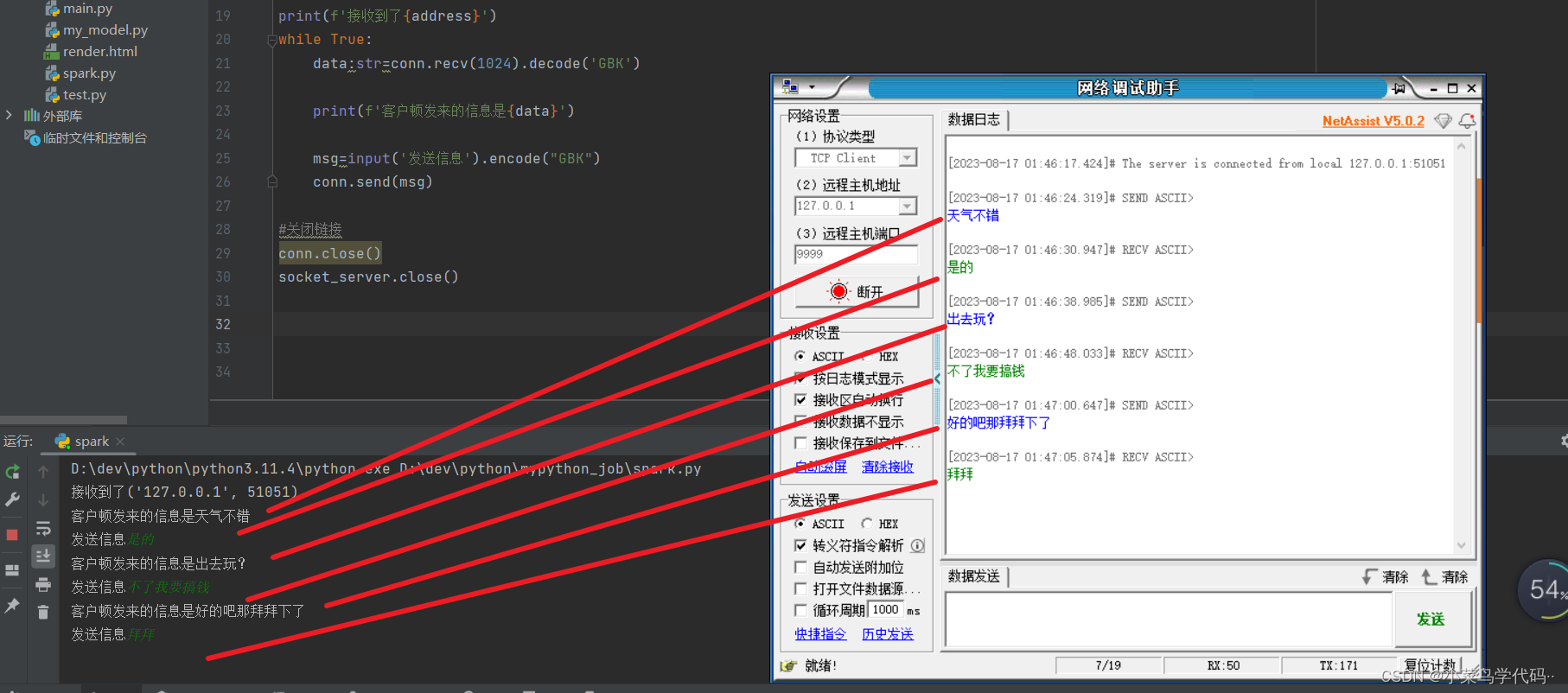
python高级基础

文章目录 python高级基础闭包修饰器单例模式跟工厂模式工厂模式单例模式 多线程多进程创建websocket服务端手写客户端 python高级基础 闭包 简单解释一下闭包就是可以在内部访问外部函数的变量&#xff0c;因为如果声明全局变量&#xff0c;那在后面就有可能会修改 在闭包中的…...

编程日记 2023/8/20 9:21:24

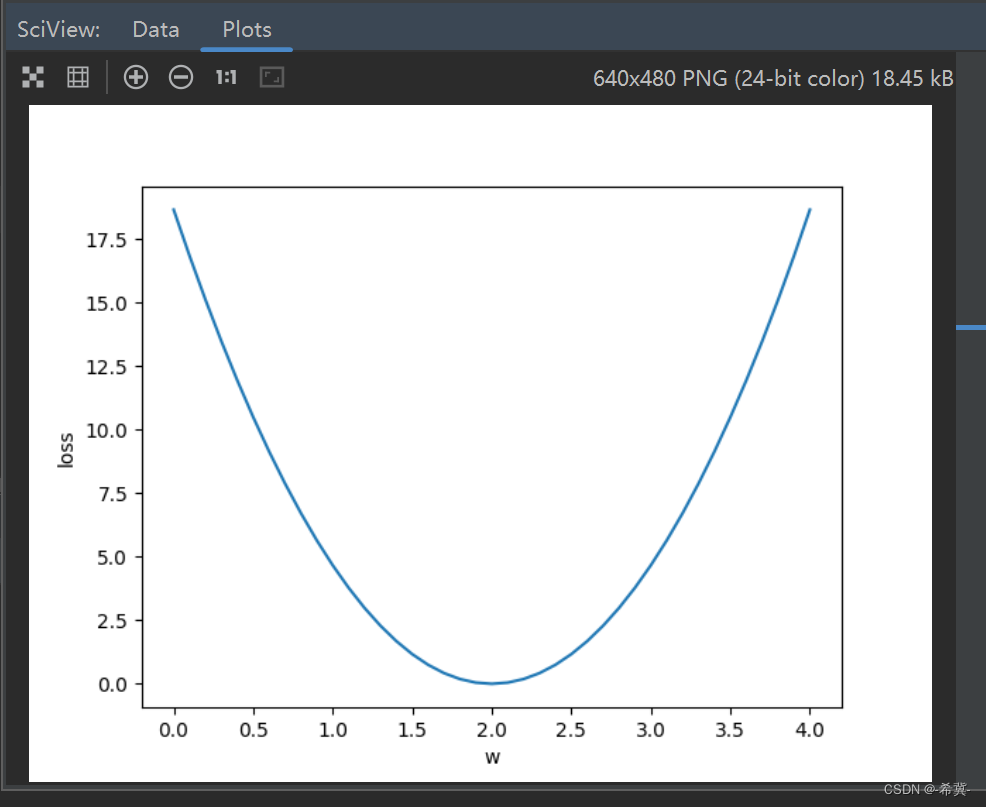
使用线性回归模型优化权重：探索数据拟合的基础

文章目录 前言一、示例代码二、示例代码解读1.线性回归模型2.MSE损失函数3.优化过程4.结果解读 总结 前言 在机器学习和数据科学中&#xff0c;线性回归是一种常见而重要的方法。本文将以一个简单的代码示例为基础&#xff0c;介绍线性回归的基本原理和应用。将使用Python和Nu…...

编程日记 2023/8/20 9:20:22

亿级短视频，如何架构？

说在前面 在尼恩的&#xff08;50&#xff09;读者社群中&#xff0c;经常指导大家面试架构&#xff0c;拿高端offer。 前几天&#xff0c;指导一个年薪100W小伙伴&#xff0c;拿到字节面试邀请。 遇到一个 非常、非常高频的一个面试题&#xff0c;但是很不好回答&#xff0…...

编程日记 2023/8/20 9:19:21

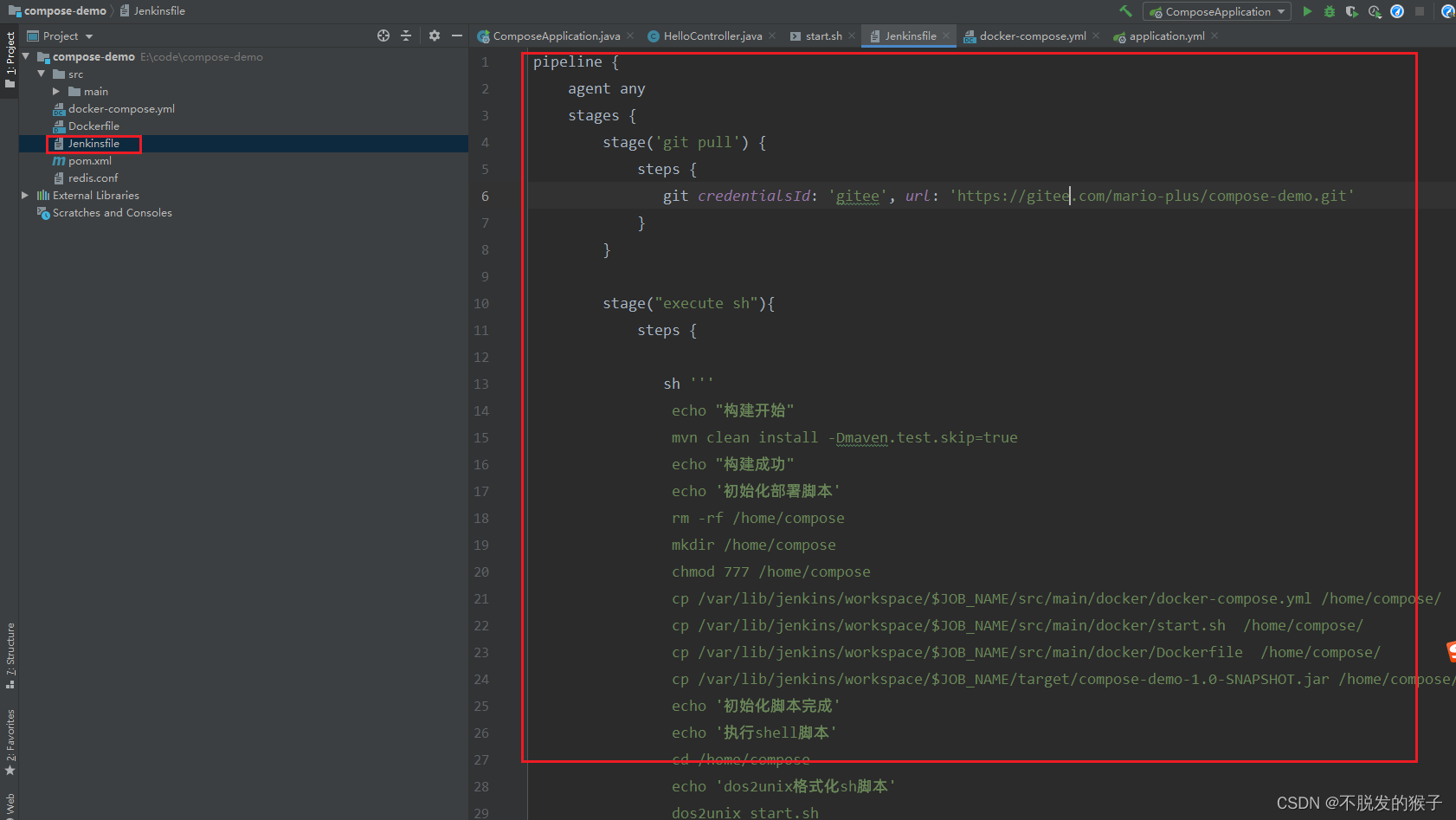
jenkins pipeline方式一键部署github项目

上篇&#xff1a;jenkins一键部署github项目 该篇使用jenkins pipeline-script一键部署&#xff0c;且介绍pipeline-scm jenkins环境配置 前言&#xff1a;按照上篇创建pipeline任务&#xff0c;结果报mvn&#xff0c;jdk环境不存在&#xff0c;就很疑惑&#xff0c;然后配置全…...

编程日记 2023/8/20 9:18:20

Vue 项目搭建

环境配置 1. 安装node.js 官网&#xff1a;nodejs&#xff08;推荐 v10 以上&#xff09; 官网&#xff1a;npm 是什么&#xff1f; 由于vue的安装与创建依赖node.js&#xff08;JavaScript的运行环境&#xff09;里的npm&#xff08;包管理和分发工具&#xff09;&#xff…...

编程日记 2023/8/20 9:17:16

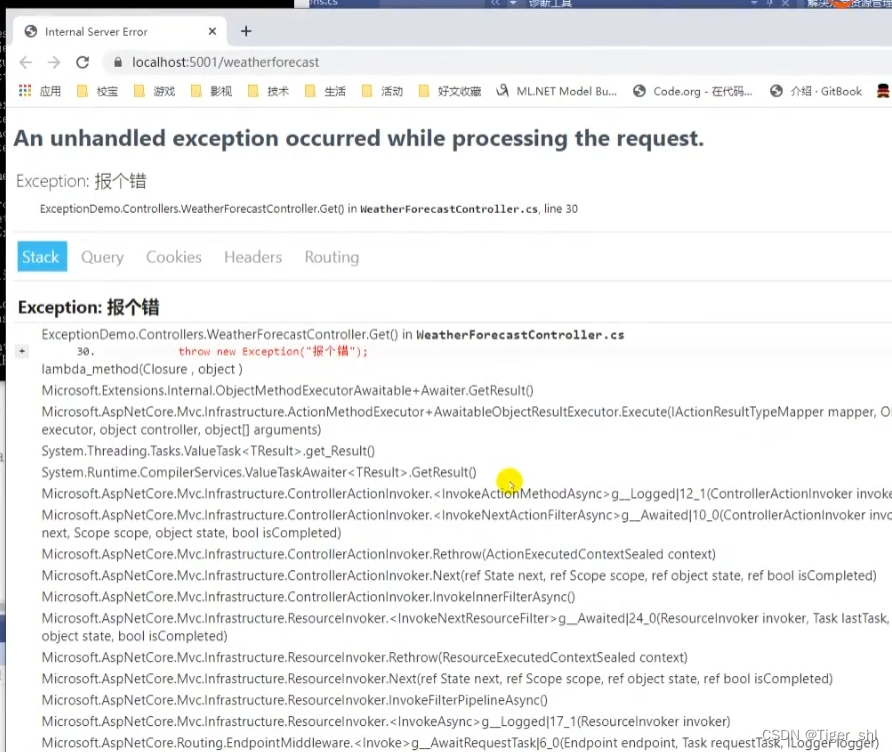
【NetCore】09-中间件

文章目录 中间件&#xff1a;掌控请求处理过程的关键1. 中间件1.1 中间件工作原理1.2 中间件核心对象 2.异常处理中间件:区分真异常和逻辑异常2.1 处理异常的方式2.1.1 日常错误处理--定义错误页的方法2.1.2 使用代理方法处理异常2.1.3 异常过滤器 IExceptionFilter2.1.4 特性过…...

编程日记 2023/8/20 9:16:15

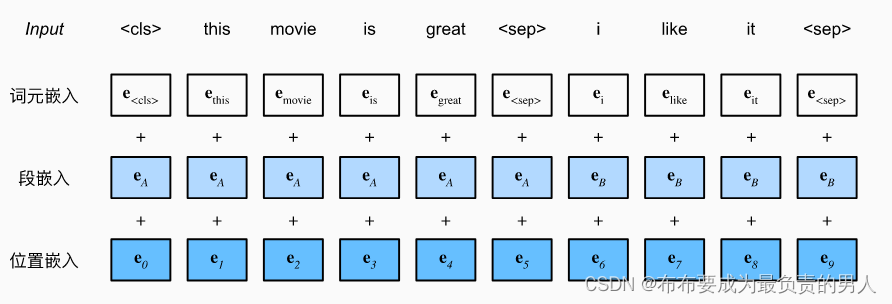
机器学习深度学习——BERT（来自transformer的双向编码器表示）

&#x1f468;‍&#x1f393;作者简介&#xff1a;一位即将上大四&#xff0c;正专攻机器学习的保研er &#x1f30c;上期文章&#xff1a;机器学习&&深度学习——transformer&#xff08;机器翻译的再实现&#xff09; &#x1f4da;订阅专栏&#xff1a;机器学习&am…...

编程日记 2023/8/20 9:15:14

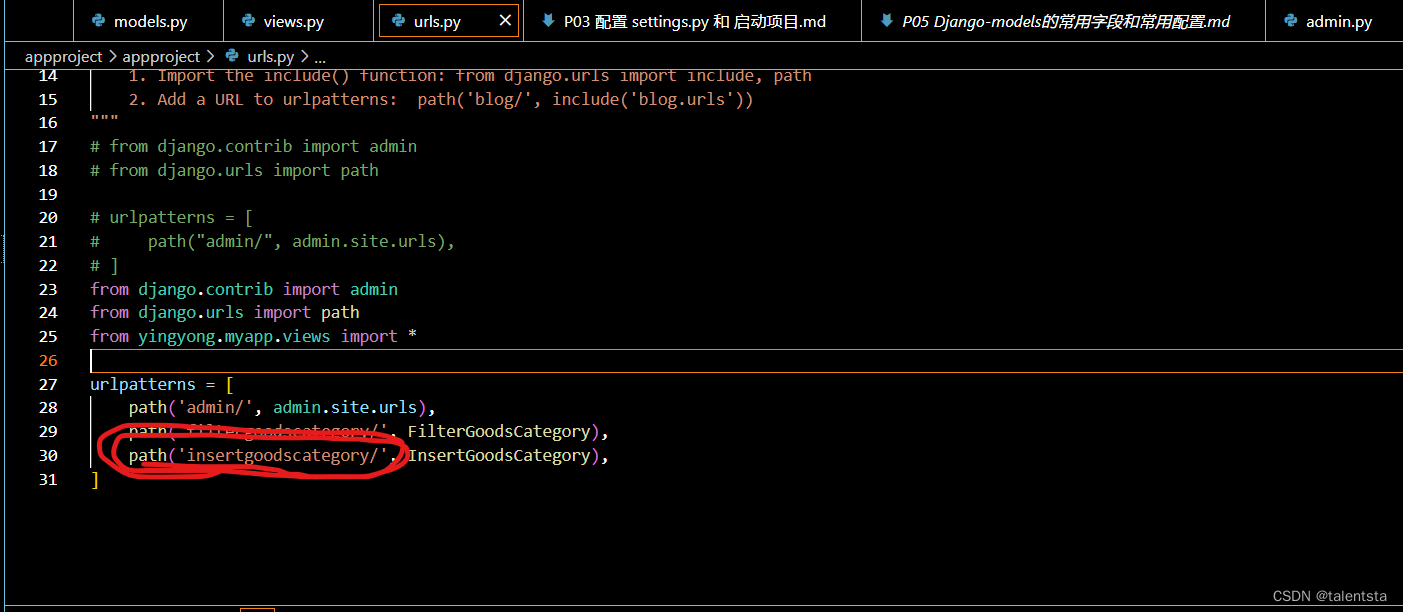
Datawhale Django后端开发入门 Vscode TASK02 Admin管理员、外键的使用

一.Admin管理员的使用 1、启动django服务 使用创建管理员之前&#xff0c;一定要先启动django服务&#xff0c;虽然TASK01和TASK02是分开的&#xff0c;但是进行第二个流程的时候记得先启动django服务&#xff0c;注意此时是在你的项目文件夹下启动的&#xff0c;时刻注意要执…...

编程日记 2023/8/20 9:14:13

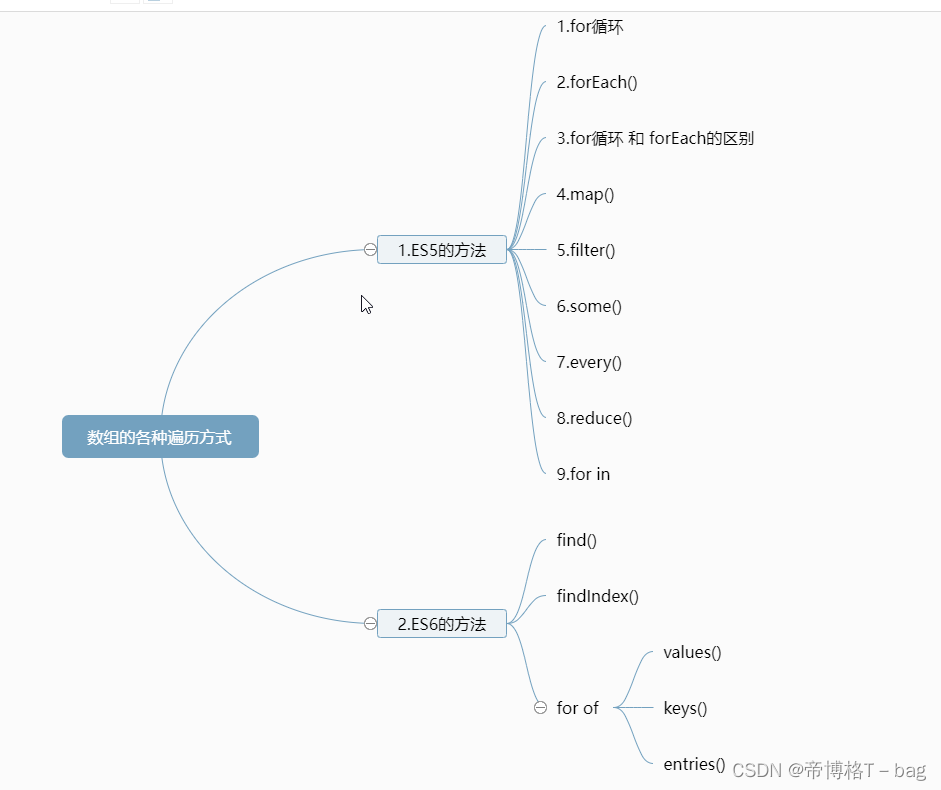
【ES5和ES6】数组遍历的各种方法集合

一、ES5的方法 1.for循环 let arr [1, 2, 3] for (let i 0; i < arr.length; i) {console.log(arr[i]) } // 1 // 2 // 32.forEach() 特点&#xff1a; 没有返回值&#xff0c;只是针对每个元素调用func三个参数&#xff1a;item, index, arr &#xff1b;当前项&#…...

编程日记 2023/8/20 9:13:12

学科在线教育元宇宙VR虚拟仿真平台落实更高质量的交互学习

为推动教育数字化&#xff0c;建设全民终身学习的学习型社会、学习型大国&#xff0c;元宇宙企业深圳华锐视点深度融合VR虚拟现实、数字孪生、云计算和三维建模等技术&#xff0c;搭建教育元宇宙平台&#xff0c;为学生提供更加沉浸式的学习体验&#xff0c;提高学习效果和兴趣…...

编程日记 2023/8/20 9:12:10

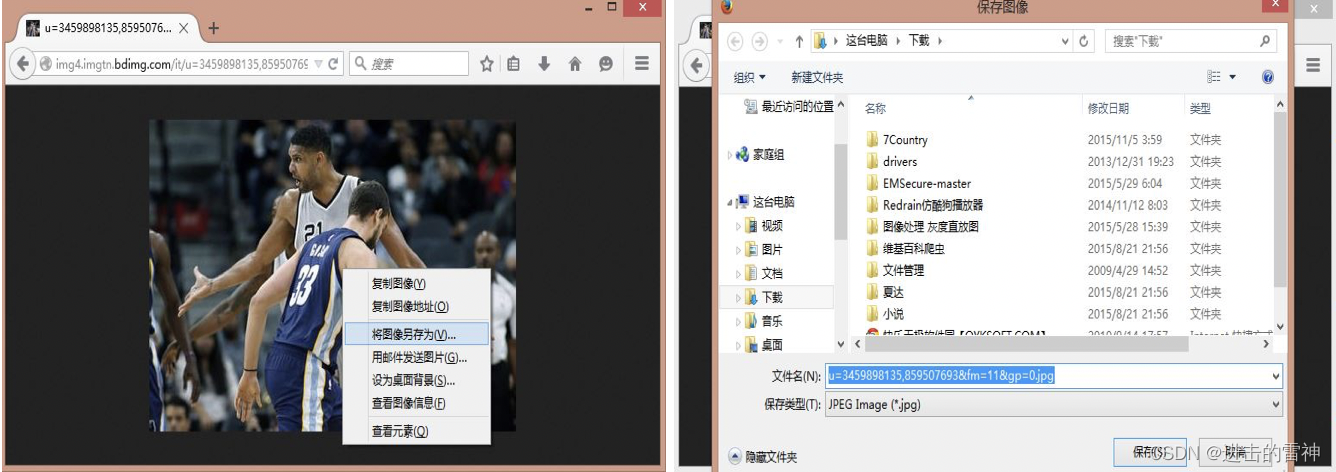
[python爬虫] 爬取图片无法打开或已损坏的简单探讨

本文主要针对python使用urlretrieve或urlopen下载百度、搜狗、googto&#xff08;谷歌镜像&#xff09;等图片时&#xff0c;出现"无法打开图片或已损坏"的问题&#xff0c;作者对它进行简单的探讨。同时&#xff0c;作者将进一步帮你巩固selenium自动化操作和urllib…...

编程日记 2023/8/20 9:11:07

手游刚开服就被攻击怎么办？如何防御DDoS？

开服初期是手游最脆弱的阶段&#xff0c;极易成为DDoS攻击的目标。一旦遭遇攻击&#xff0c;可能导致服务器瘫痪、玩家流失&#xff0c;甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案&#xff0c;帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

编程新知 2026/2/8 4:37:03

python打卡day49

知识点回顾&#xff1a; 通道注意力模块复习空间注意力模块CBAM的定义 作业&#xff1a;尝试对今天的模型检查参数数目&#xff0c;并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

编程新知 2026/2/7 5:37:17

云启出海，智联未来｜阿里云网络「企业出海」系列客户沙龙上海站圆满落地

借阿里云中企出海大会的东风&#xff0c;以**「云启出海&#xff0c;智联未来&#xff5c;打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办&#xff0c;现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

编程新知 2026/1/30 0:00:28

MODBUS TCP转CANopen 技术赋能高效协同作业

在现代工业自动化领域&#xff0c;MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步&#xff0c;这两种通讯协议也正在被逐步融合&#xff0c;形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

编程新知 2026/2/6 9:48:02

ETLCloud可能遇到的问题有哪些？常见坑位解析

数据集成平台ETLCloud&#xff0c;主要用于支持数据的抽取&#xff08;Extract&#xff09;、转换&#xff08;Transform&#xff09;和加载&#xff08;Load&#xff09;过程。提供了一个简洁直观的界面&#xff0c;以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

编程新知 2026/2/3 12:56:31

【HTML-16】深入理解HTML中的块元素与行内元素

HTML元素根据其显示特性可以分为两大类&#xff1a;块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

编程新知 2025/11/11 6:28:42

自然语言处理——循环神经网络

自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元&#xff08;GRU&#xff09;长短期记忆神经网络&#xff08;LSTM&#xff09…...

编程新知 2026/2/4 11:21:40

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统

目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索&#xff08;基于物理空间 广播范围&#xff09;2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

编程新知 2025/12/12 6:01:17

是否存在路径（FIFOBB算法）

题目描述 一个具有 n 个顶点e条边的无向图&#xff0c;该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序&#xff0c;确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数&#xff0c;分别表示n 和 e 的值&#xff08;1…...

编程新知 2025/10/1 6:09:21

优选算法第十二讲：队列 + 宽搜 优先级队列

优选算法第十二讲&#xff1a;队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

编程新知 2026/1/20 17:18:59