C语言小练习(一)

🌞 “人生是用来体验的,不是用来绎示完美的,接受迟钝和平庸,允许出错,允许自己偶尔断电,带着遗憾,拼命绽放,这是与自己达成和解的唯一办法。放下焦虑,和不完美的自己和解,然后去爱那个完整的自己!”
前面,关于C语言的基础知识都学的差不多,但是想要好好掌握这门语言,还是要勤加练习,从现在到开学,每天会更新一个小练笔,大家可以一起来做一下❗
Day01
- 📝 一.选择题
- 📝二.编程题
📝 一.选择题
1.🎈执行下面程序,正确的输出是( )
#include <stdio.h>
int x = 5, y = 7;
void swap()
{int z;z = x;x = y;y = z;
}
int main()
{int x = 3, y = 8;swap();printf("%d,%d\n", x, y);return 0;
}
A: 5,7 B: 7,5 C: 3,8 D: 8,3
🏆答案:C
🔭答题思路:swap函数调用的是全局变量,int x = 3, y = 8;属于局部变量,只在主函数内生效。而主函数内的printf函数考虑局部优先的原则,会输出3,8。
2.🎈以下不正确的定义语句是( )
A: double x[5] = {2.0, 4.0, 6.0, 8.0, 10.0};
B: char c2[] = {‘\x10’, ‘\xa’, ‘\8’};
C: char c1[] = {‘1’,‘2’,‘3’,‘4’,‘5’};
D: int y[5+3]={0, 1, 3, 5, 7, 9};
🏆答案:B
🔭答题思路:这里的B选项,就用到了转义字符的知识,详细的也可以去看我另外一篇博客:链接: 转义字符
✅ 这里,我们就知道\ddd中ddd表示1~3个八进制的数字。如:\130 X
八进制数是由0~7组成,题目中B选项就错在了'\8'中出现了8.
而\ xdd中dd表示2个十六进制的数字。如:\x30 0
十六进制的数是由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A-F分别表示十进制数字10-15.
3.🎈 test.c 文件中包括如下语句,文件中定义的四个变量中,是指针类型的变量为【多选】( )
#define INT_PTR int*
typedef int* int_ptr;
INT_PTR a, b;
int_ptr c, d;
A: a B: b C: c D: d
🏆答案:ACD
🔭答题思路:本题主要需要弄清楚define和typedef。#define是一种宏,一般会用在预处理阶段,在预处理阶段,define只会替换,不会做任何的算计逻辑等处理。而typedef是关键字,在编译时处理,有类型检查功能。它在自己的作用域内给一个已经存在的类型一个别名,但不能在一个函数定义里面使用typedef。用typedef定义数组、指针、结构等类型会带来很大的方便,不仅使程序书写简单,也使意义明确,增强可读性。
🔎那么,在上述代码中,INT_PTR a, b;在预处理阶段就会转化成int*a,b;这里,int *是a的类型,而b的类型是int.而typedef是起了一个别名,别名是一个独立的类型,使用这个类型创建的变量都是这个类型,因此c和d都是int*.
我们也可以通过调试来验证一下:
4.🎈若给定条件表达式 (M)?(a++):(a–) ,则其中表达式 M ( )
A: 和(M==0)等价 B: 和(M ==1)等价C: 和(M!=0)等价 D: 和(M!=1)等价
🏆答案:B
🔭答题思路:本题考察的主要是三目运算符表达式1?表达式2:表达式3
✅唯一 一个三目操作符。
🧩表达式1为真,表达式2的结果为整个表达式的结果,表达式3不算.
🧩表达式1为假,表达式3的结果为整个表达式的结果,表达式2不算。
关于操作符的详细知识点,可以跳转见博客:操作符(上)
操作符(下)本题只要知道了操作符的相关知识,就不难解出!
5.🎈有如下定义语句,则正确的输入语句是【多选】( )
int b;
char c[10];
A: scanf(“%d%s”,&b,&c); B: scanf(“%d%s”,&b,c);
C: scanf(“%d%s”,b,c); D: scanf(“%d%s”,b,&c);
🏆答案:AB
🔭答题思路:作为字符数组,c和&c的地址一致,但是,对于整型变量b,想要取它的地址,必须是&b.
📝二.编程题
1.🎈输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
- 用返回一个整数列表来代替打印
- n 为正整数,0 < n <= 5
OJ链接【牛客网题号: JZ17 打印从1到最大的n位数】【难度:入门】
🔭答题思路:从题目中,我们知道
n的取值范围是正整数1~5,当n为1,应当输出[1,2,3,4,5,6,7,8,9]当n为2时,应当输出[1,2,3...99],当n为3,应当输出[1,2,3...999]当n为4时,应当输出[1,2,3...9999]当n为5时,应当输出[1,2,3...99999]我们发现最大的那位数都可以用10^n^-1来表示,那么打印的过程,我们可以用for循环来实现。
int* printNumbers(int n, int* returnSize)
{*returnSize = pow(10, n) - 1;int* ret = (int*)malloc(sizeof(int) * (*returnSize));//申请足够大的空间//malloc函数是用于动态内存分配的int i = 0;for (i = 0; i < *returnSize; i++){*(ret + i) = i + 1;//下标从0开始,数值从1开始}return ret;
}

📖malloc是动态内存分配函数,用于申请一块连续的指定大小的内存块区域以void*类型返回分配的内存区域地址。如果分配成功则返回指向被分配内存的指针,否则返回空指针NULL。
✅注意:malloc函数的返回的是无类型指针,在使用时一定要强制转换为所需要的类型。❗
🏆在使用malloc开辟空间时,使用完成一定要释放空间,如果不释放会造内存泄漏。
🔎在使用malloc函数开辟的空间中,不要进行指针的移动,因为一旦移动之后可能出现申请的空间和释放空间大小的不匹配。
📝具体使用方法:指针自身 = (指针类型*)malloc(sizeof(指针类型)*数据数量)
2.🎈根据输入的日期,计算是这一年的第几天。输入保证年份为4位数且日期合法。
输入描述:输入一行,每行空格分割,分别是年,月,日。
输出描述:输出是这一年的第几天
OJ链接【牛客网题号: HJ73 计算日期到天数转换】【难度:简单】
🔭答题思路:拿到这个题目,我们首先想到的是,我们需要
判断这一年是否为闰年,闰年的二月有29天,而其他普通年份二月只有28天。那么如果月份大于2,总天数就要进行+1的操作。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
int main()
{int year = 0, month = 0, day = 0;scanf("%d%d%d", &year, &month, &day);int month_day[12] = { 31,59,90,120,151,181,212,243,273,304,334,365 };//建立一个整型数组,表示普通年份,前month个月数的天数和int days = 0;if (month >= 2){days = month_day[month - 2] + day;}elsedays = day;if (month > 2){if (year % 4 == 0 && year % 100 != 0 || year % 400 == 0)//如果是闰年,天数+1{days++;}}printf("%d\n", days);return 0;
}

好啦,第一天的练习到这里就结束啦!后期会继续更新C语言的小练笔,欢迎大家持续关注、点赞和评论!❤️❤️❤️
相关文章:

C语言小练习(一)
🌞 “人生是用来体验的,不是用来绎示完美的,接受迟钝和平庸,允许出错,允许自己偶尔断电,带着遗憾,拼命绽放,这是与自己达成和解的唯一办法。放下焦虑,和不完美的自己和解…...

Flask-flask系统运行后台轮询线程
对于有些flask系统,后台需要启动轮询线程,执行特定的任务,以下是一个简单的例子。 globals/daemon.py import threading from app.executor.ops_service import find_and_run_ops_task_todo_in_redisdef context_run_func(app, func):with …...

jsp本质-servlet
jsp本质-servlet 一、jsp文件 <% page language"java" contentType"text/html; charsetUTF-8" pageEncoding"UTF-8"%> <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>JSP Example…...

回归预测 | MATLAB实现GWO-SVM灰狼优化算法优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GWO-SVM灰狼优化算法优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GWO-SVM灰狼优化算法优化支持向量机多输入单输出回归预测(多指标,多图)效果一览基…...

科技资讯|苹果Vision Pro新专利曝光:可调节液态透镜
苹果公司近日申请了名为“带液态镜头的电子设备”,概述了未来可能的头显设计。头显设备中的透镜采用可调节的液态透镜,每个透镜可以具有填充有液体的透镜腔,透镜室可以具有形成光学透镜表面的刚性和 / 或柔性壁。 包括苹果自家的 Vision Pr…...

神经网络基础-神经网络补充概念-38-归一化输入
概念 归一化输入是一种常见的数据预处理技术,旨在将不同特征的取值范围映射到相似的尺度,从而帮助优化机器学习模型的训练过程。归一化可以提高模型的收敛速度、稳定性和泛化能力,减少模型受到不同特征尺度影响的情况。 常见的归一化方法 …...

【Redis】什么是缓存雪崩,如何预防缓存雪崩?
【Redis】什么是缓存雪崩,如何预防缓存雪崩? 如果缓存集中在一段时间内失效,也就是通常所说的热点数据集中失效 (一般都会给缓存设定一个失效时间,过了失效时间后,该数据库会被缓存直接删除,从…...

[国产MCU]-W801开发实例-开发环境搭建
W801开发环境搭建 文章目录 W801开发环境搭建1、W801芯片介绍2、W801芯片特性3、W801芯片结构4、开发环境搭建1、W801芯片介绍 W801芯片是联盛德微电子推出的一款高性价比物联网芯片。 W801 芯片是一款安全 IoT Wi-Fi/蓝牙 双模 SoC芯片。芯片提供丰富的数字功能接口。支持2.…...
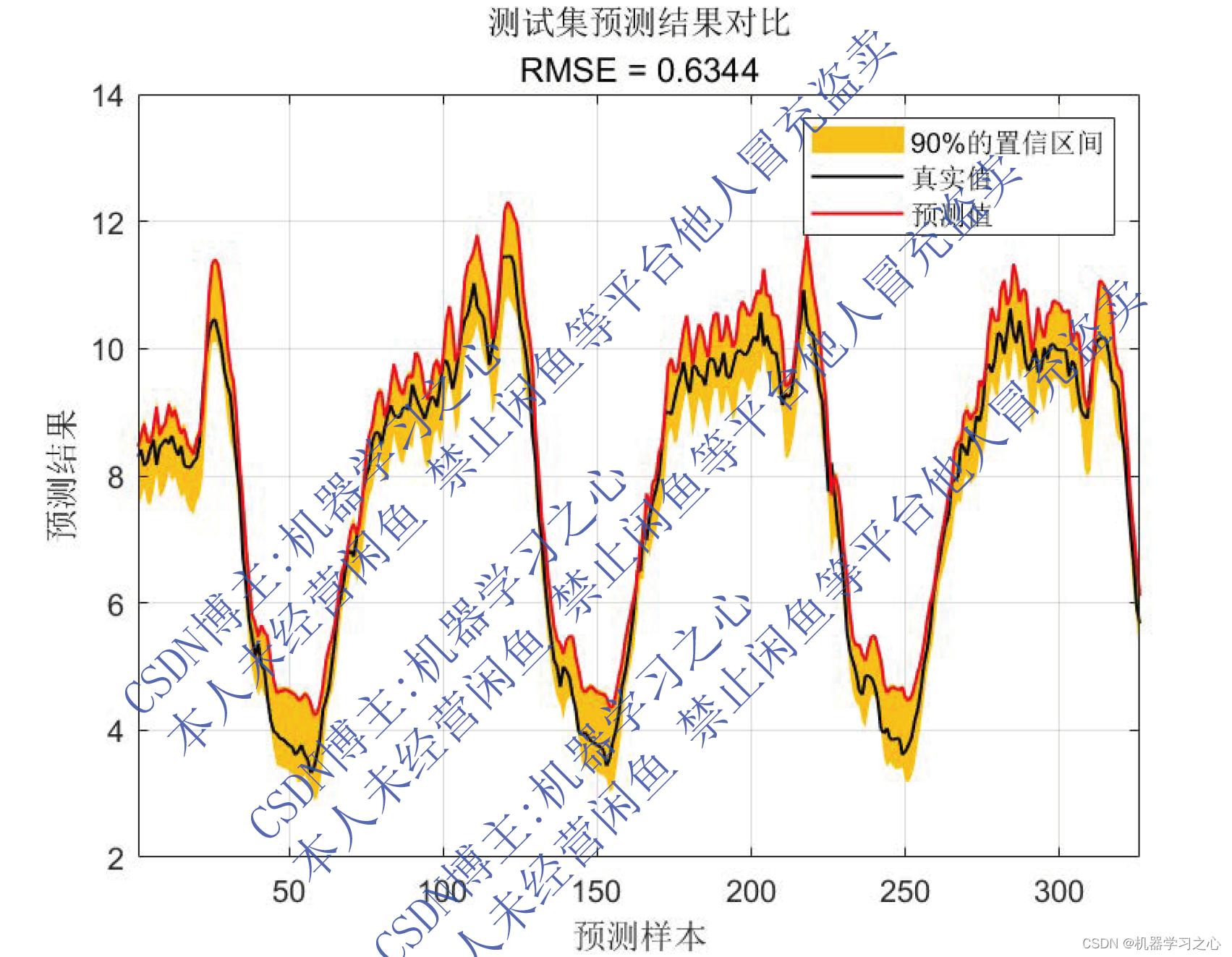
区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测
区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测 目录 区间预测 | MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测效果一览基本介绍模型描述程序设计参考资料 效果一览 基本介绍 MATLAB实现QRGRU门控循环单元分位数回归时间序列区间预测。基于分位…...
改善神经网络——优化算法(mini-batch、动量梯度下降法、Adam优化算法)
改善神经网络——优化算法 梯度下降Mini-batch 梯度下降(Mini-batch Gradient Descent)指数加权平均包含动量的梯度下降RMSprop算法Adam算法 优化算法可以使神经网络运行的更快,机器学习的应用是一个高度依赖经验的过程,伴随着大量…...
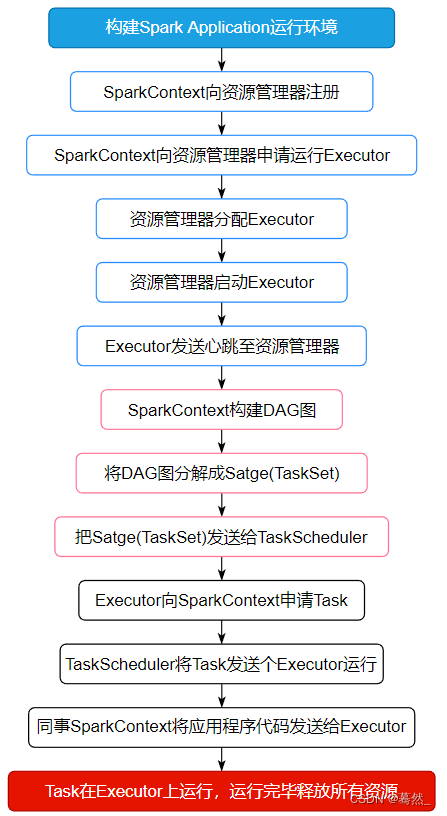
大数据面试题:Spark的任务执行流程
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)Spark的工作流程?2)Spark的调度流程;3)Spark的任务调度原理…...

通过 Amazon SageMaker JumpStart 部署 Llama 2 快速构建专属 LLM 应用
来自 Meta 的 Llama 2 基础模型现已在 Amazon SageMaker JumpStart 中提供。我们可以通过使用 Amazon SageMaker JumpStart 快速部署 Llama 2 模型,并且结合开源 UI 工具 Gradio 打造专属 LLM 应用。 Llama 2 简介 Llama 2 是使用优化的 Transformer 架构的自回归语…...

ansible远程执行命令
一、ansible简介 需要在一台机器上搭建ansible环境,且配置目的ip的密码,通道没有问题即可下发命令 使用的通道是ssh(端口:36000) 二、搭建细节 1、安装ansible yum install -y ansible 2、把目的ip密码写到配置…...

Windows快速恢复丢失的颜色校准
场景 有时开机或启动某个软件后,颜色校准(设置项:校准显示器颜色)会丢失,每次重新设置很麻烦。 文章首发及后续更新:https://mwhls.top/4723.html,无图/无目录/格式错误/更多相关请至首发页查看…...

Vue安装单文件组件
安装 npm npm 全称为 Node Package Manager,是一个基于Node.js的包管理器,也是整个Node.js社区最流行、支持的第三方模块最多的包管理器。 npm -v由于网络原因 安装 cnpm npm install -g cnpm --registryhttps://registry.npm.taobao.org安装 vue-cli…...

小白的Node.js学习笔记大全---不定期更新
Node.js是什么 Node. js 是一个基于 Chrome v8 引擎的服务器端 JavaScript 运行环境Node. js 是一个事件驱动、非阻塞式I/O 的模型,轻量而又高效Node. js 的包管理器 npm 是全球最大的开源库生态系统 特性 单一线程 Node.js 沿用了 JavaScript 单一线程的执行特…...
)
第二周晨考自测(2.0)
1.冒泡排序 冒泡排序是数组解构中的常见排序算法之一。规则如下:先遍历数组,让相邻的两个数据进行比较,如果前一个比后一个大,那么就把这两个数据交换位置,经过一轮遍历之后,最大的那个数字就排在数组最后…...
(单视图测量))
计算机视觉之三维重建(三)(单视图测量)
2D变换 等距变换 旋转平移保留形状、面积通常描述刚性物体运动 相似变换 在等距变换的基础增加缩放特点 射影变换 共线性、四共线点的交比保持不变 仿射变换 面积比值、平行关系等不变仿射变换是特殊的射影变换 影消点与影消线 2D无穷远点 两直线的交点可由两直线的…...

docker 批量快速删除容器和镜像
一、批量删除镜像 如果你想要批量删除 Docker 镜像,可以使用各种命令。以下是一些示例: 1. 删除所有镜像: docker rmi $(docker images -q) 2. 删除所有未标记的镜像(即 <none> 镜像): docker rmi $(docker images -f "dangling=true" -q) 请注意…...
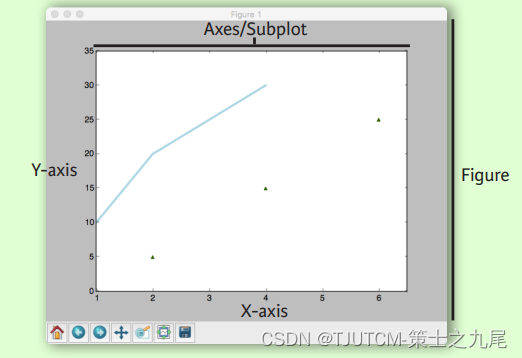
【数据分析入门】Matplotlib
目录 零、图形解析与工作流0.1 图形解析0.2 工作流 一、准备数据1.1 一维数据1.2 二维数据或图片 二、绘制图形2.1 画布2.2 坐标轴 三、绘图例程3.1 一维数据3.2 向量场3.3 数据分布3.4 二维数据或图片 四、自定义图形4.1 颜色、色条与色彩表4.2 标记4.3 线型4.4 文本与标注4.5…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...


