数据结构——B-树、B+树、B*树
一、B-树
1. B-树概念
B树是一种适合外查找的、平衡的多叉树。一棵m阶(m>2)的B树,是一棵平衡的M路平衡搜索树,它可以是空树或满足以下性质:
(1)根节点至少有两个孩子。
(2)每个分支节点都包含k-1个关键字和k个孩子,其中ceil(m/2)<= k <= m。(ceil表示向上取整)
(3)每个叶子节点都包含k-1个关键字,其中ceil(m/2)<= k <= m。
(4)所有叶子节点都在同一层。
(5)每个节点中的关键字从小到大排列,节点中k-1个元素正好是k个孩子包含的元素的值域划分。
(6)每个节点的结构为:(n, A0, K1, A1, K2, A2……, Kn, An),其中Ki(1<=i<=n)为关键字,且ki<ki + 1(1<=i<=n)。Ai(0<=i<=n)为指向子树根节点的指针,且Ai所指子树所有节点中的关键字均小于Ki+1。n为节点中关键字的个数,满足ceil(m/2)-1 <=n <= m-1。
2. B树的插入
采用m为3的一棵三叉B树的插入过程进行演示。根据B树性质可知,m为3,则每个节点最多有三个孩子(m-1个),每个节点包含k-1个关键字,2<=k<=3。注意:插入只能插入到叶子节点。
(1)首先插入两个值20,30

(2)插入第三个值25,由于每个节点最多有2个关键字,所以此时会进行分裂来维持B树平衡。
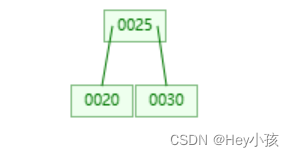
2.1 B树分裂规则
创建一个兄弟节点,拷贝当前节点内右半区间的数据到兄弟节点中,保留当前节点中左半区间的数据,将该节点内的中位数提到父节点中(若没有父节点,则创建新的父节点)。
(3)插入35

(4) 插入40
此时根节点的右侧孩子内数据超过2个,则按照B树分裂规则分裂后如下:
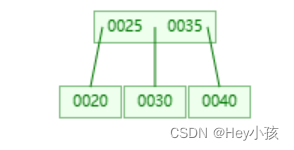
(5)插入33
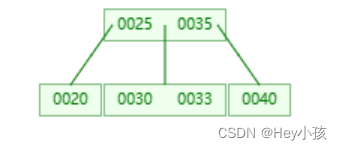
(6)插入34
此时根节点的中间孩子内数据超过2两个,进行分裂,当提取33到父节点后,根节点内数据也超过了2个,则根节点也会进行分裂,此时没有父节点,则会创建新的父节点,结构如下:
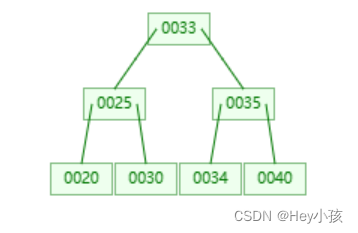
三、B+树
1. B+树概念
B+树是B树的变形,它是在B树基础上进行优化的多路平衡搜索树,B+树的规则和B树基本类似,但在其基础上进行了以下优化:
(1)分支节点的子树指针与关键字个数相同;
(2)分支节点的子树指针p[i]指向关键字值大小在[k[i], k[i+1]]之间;
(3)所有叶子节点增加一个链接指针链接在一起;
(4)所有关键字及其映射数据都在叶子节点出现。
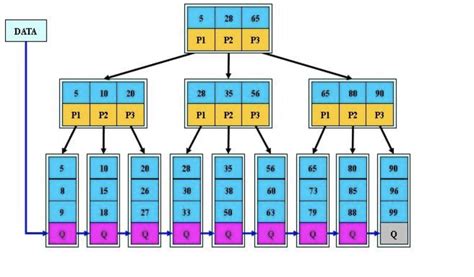
优点:
(1)简化了B树孩子币关键字多一个的规则,由多一个变成相等。
(2)所有值都在叶子节点中,且叶子节点通过指针链接起来,方便遍历。
2. B+树的插入
B+树的插入过程与B树基本类似,区别在于:
(1)第一次插入两层节点,一层做分支,一层做根;
(2)B+树在分裂时,是将左半部分的数据保留,右半部分的数据放入新建兄弟节点中,并将新建节点中的最小值更新到父节点中。
三、B*树
1. B*树概念
B*树又是B+树的变形,做了以下改动:
(1)在B+树的非根和非叶子节点再增加指向兄弟节点的指针。
(2)节点在分裂时,保证每个节点中值的数量至少为2/3 * M,最多为M个,也就是从1/2提高到了2/3,提高空间利用率。
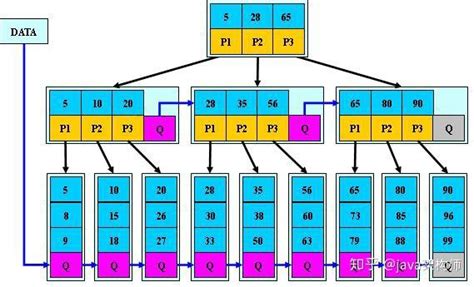
2. B*树的插入
B*树的插入与B+树基本类似,区别主要在于分裂规则,B*树的分裂规则:
如果它的下一个兄弟节点未满,则将一部分数据移到兄弟节点中,再在原节点中插入关键字,最后修改父节点中兄弟节点的关键字(因为兄弟节点的关键字范围发生了变化);
如果兄弟节点也满了,则在原节点与兄弟节点之间添加新节点,并各复制1/3的数据到新节点中,最后在父节点中添加新节点的指针。
四、B树系列的优缺点
1. 优点
(1)高效的查找操作:B树系列的数据结构通过将数据分布在多层节点上,使用索引快速导航到目标元素所在的叶子节点,从而实现了高效的查找操作。其时间复杂度通常为O()
(2)适应大规模数据集:B树系列的数据结构能够充分利用磁盘块的大小,减少磁盘I/O操作的次数,提高存储和访问效率。它们被广泛应用于数据库索引、文件系统等需要处理大规模数据集的场景。
(3)自平衡特性:B树系列的数据结构通过节点的分裂和合并来自动保持树的平衡,保证了各个节点的高度相对较小,从而维持了高效的操作性能。
(4)支持范围查询:由于B树系列的数据结构中数据是按照键的大小顺序进行排序,因此可以很方便地进行范围查询操作。
2. 缺点
(1)空间利用率低,消耗高。
(2)插入删除数据、分裂合并节点,都必然存在数据挪动。
(3)虽然B树系列的高度更低,但是在内存中和哈希、平衡搜索树的查找效率处于同一量级。
相关文章:
数据结构——B-树、B+树、B*树
一、B-树 1. B-树概念 B树是一种适合外查找的、平衡的多叉树。一棵m阶(m>2)的B树,是一棵平衡的M路平衡搜索树,它可以是空树或满足以下性质: (1)根节点至少有两个孩子。 (2&#…...

2023国赛数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录 算法介绍FP树表示法构建FP树实现代码 建模资料 ## 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,…...

GPT系列总结
1.GPT1 无监督预训练有监督的子任务finetuning https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf 1.1 Unsupervised pre-training (1)基于一个transformer decoder,通过一个窗口的输入得…...

【福建事业单位-综合基础知识】05民法典
这里写自定义目录标题 一、民法概述概念原则总结 二、自然人概念总结 三、民事法律行为总结 民法考察2-4题(重点总则篇) 一、民法概述 概念原则 总结 二、自然人 概念 总结 三、民事法律行为 总结...

微服务篇
微服务篇 springcloud 常见组件有哪些 面试官: Spring Cloud 5大组件有哪些? 候选人: 早期我们一般认为的Spring Cloud五大组件是 Eureka:注册中心Ribbon:负载均衡Feign:远程调用Hystrix:…...
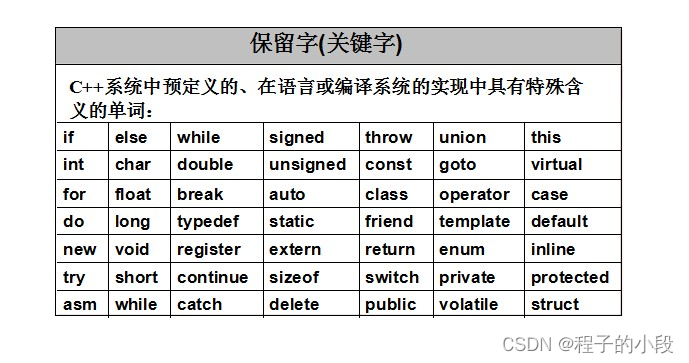
C++ 的关键字(保留字)完整介绍
1. asm asm (指令字符串):允许在 C 程序中嵌入汇编代码。 2. auto auto(自动,automatic)是存储类型标识符,表明变量"自动"具有本地范围,块范围的变量声明(如for循环体内的变量声明…...
C#小轮子:MiniExcel,快速操作Excel
文章目录 前言环境安装功能测试普通读写读新建Excel表格完全一致测试:成功大小写测试:严格大小写别名读测试:成功 写普通写别名写内容追加更新模板写 其它功能xlsx和CSV互转 前言 Excel的操作是我们最常用的操作,Excel相当于一个…...

Ribbon负载均衡
Ribbon与Eureka的关系 Eureka的服务拉取与负载均衡都是由Ribbon来实现的。 当服务发送http://userservice/user/xxxhtt://userservice/user/xxx请求时,是无法到达userservice服务的,会通过Ribbon会把这个请求拦截下来,通过Eureka-server转换…...
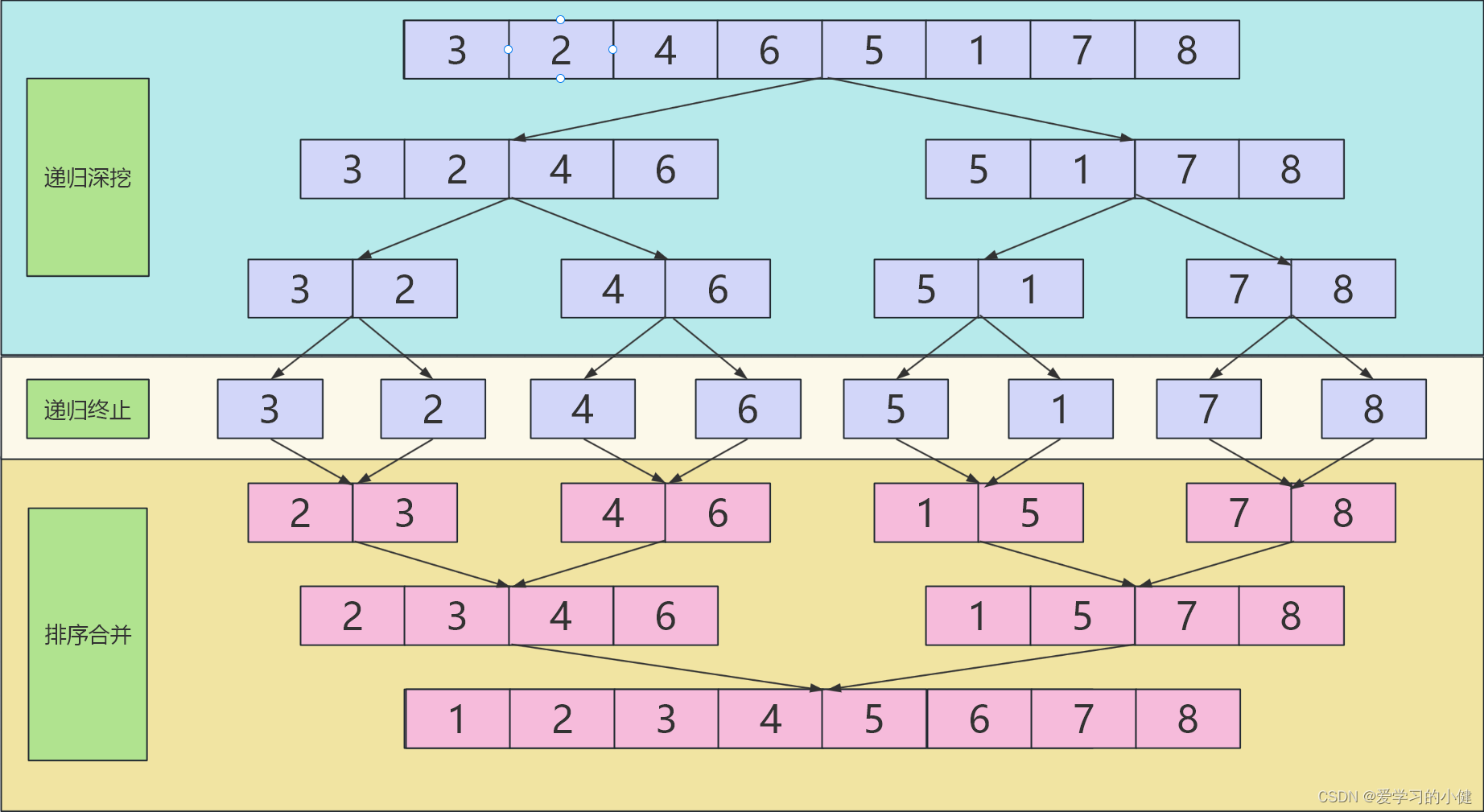
LeetCode--HOT100题(33)
目录 题目描述:148. 排序链表(中等)题目接口解题思路代码 PS: 题目描述:148. 排序链表(中等) 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 LeetCode做题链接࿱…...

【docker练习】
1.安装docker服务,配置镜像加速器 看这篇文章https://blog.csdn.net/HealerCCX/article/details/132342679?spm1001.2014.3001.5501 2.下载系统镜像(Ubuntu、 centos) [rootnode1 ~]# docker pull centos [rootnode1 ~]# docker pull ubu…...
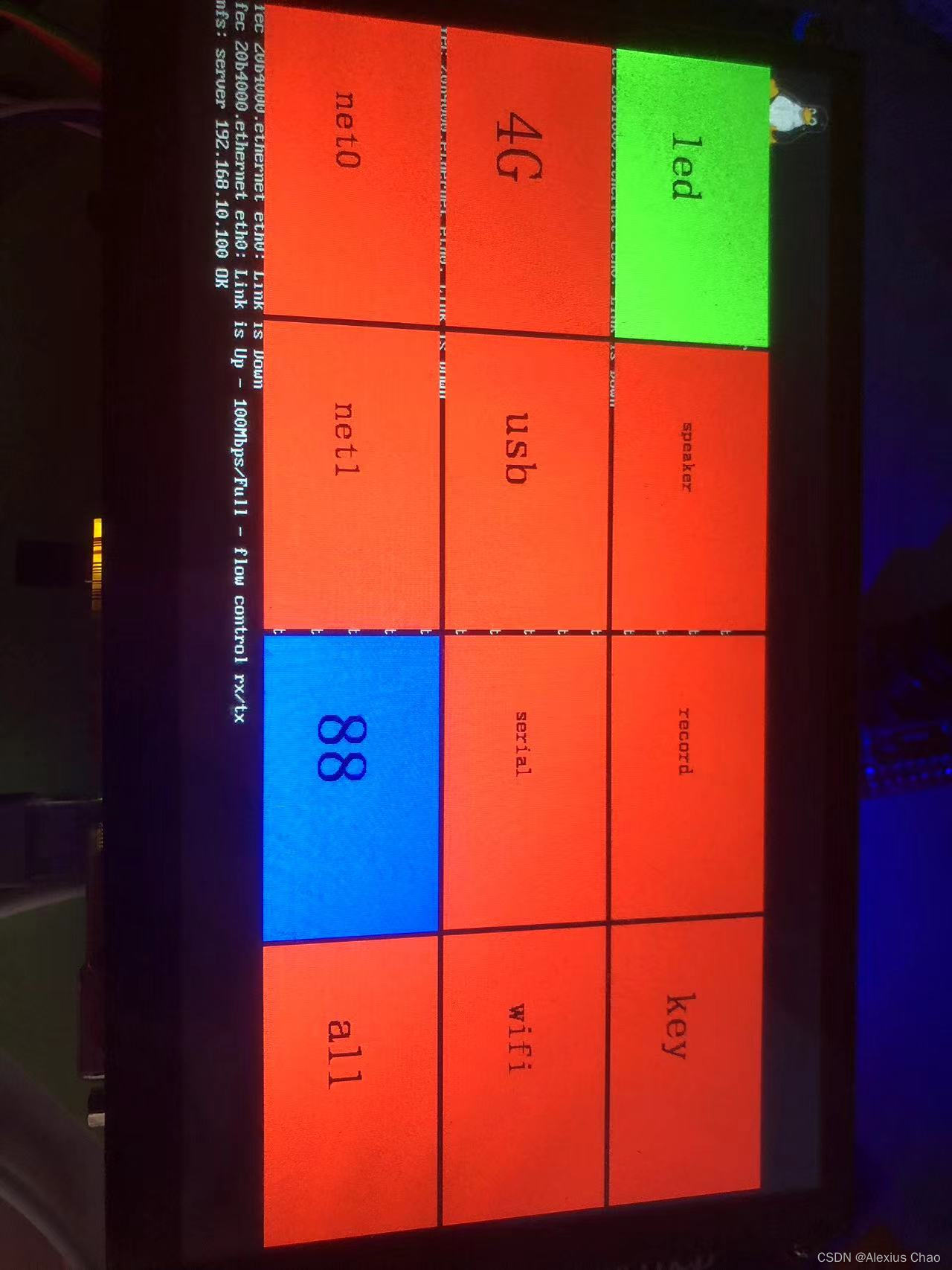
韦东山-电子量产工具项目:业务系统
代码结构 所有代码都已通过测试跑通,其中代码结构如下: 一、include文件夹 1.1 common.h #ifndef _COMMON_H #define _COMMON_Htypedef struct Region {int iLeftUpX; //区域左上方的坐标int iLeftUpY; //区域左下方的坐标int iWidth; //区域宽…...
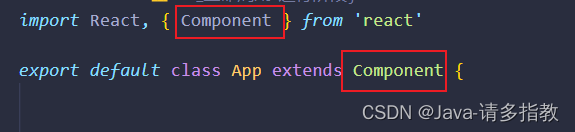
React(6)
1.React插槽 import React, { Component } from react import Child from ./compoent/Childexport default class App extends Component {render() {return (<div><Child><div>App下的div</div></Child></div>)} }import React, { Compon…...
RabbitMq-2安装与配置
Rabbitmq的安装 1.上传资源 注意:rabbitmq的版本必须与erlang编译器的版本适配 2.安装依赖环境 //打开虚拟机 yum install build-essential openssl openssl-devel unixODBC unixODBC-devel make gcc gcc-c kernel-devel m4 ncurses-devel tk tc xz3.安装erlan…...
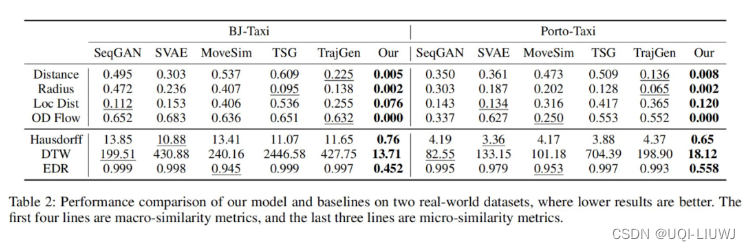
论文笔记:Continuous Trajectory Generation Based on Two-Stage GAN
2023 AAAI 1 intro 1.1 背景 建模人类个体移动模式并生成接近真实的轨迹在许多应用中至关重要 1)生成轨迹方法能够为城市规划、流行病传播分析和交通管控等城市假设分析场景提供仿仿真数据支撑2)生成轨迹方法也是目前促进轨迹数据开源共享与解决轨迹数…...

redis实战-缓存数据解决缓存与数据库数据一致性
缓存的定义 缓存(Cache),就是数据交换的缓冲区,俗称的缓存就是缓冲区内的数据,一般从数据库中获取,存储于本地代码。防止过高的数据访问猛冲系统,导致其操作线程无法及时处理信息而瘫痪,这在实际开发中对企业讲,对产品口碑,用户评价都是致命的;所以企业非常重视缓存…...

【排序】选择排序
文章目录 选择排序时间复杂度空间复杂度稳定性 代码 选择排序 以从小到大为例进行说明。 选择排序就是定义出一个最小值下标,然后遍历整个剩下的数组选择出最小的放进最小值下标的位置。 时间复杂度 O(N) 遍历一次即可 空间复杂度 O(1) 稳定性 不稳定 代码 p…...

深入浅出Pytorch函数——torch.nn.init.trunc_normal_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...

探索高级UI、源码解析与性能优化,了解开源框架及Flutter,助力Java和Kotlin筑基,揭秘NDK的魅力!
课程链接: 链接: https://pan.baidu.com/s/13cR0Ip6lzgFoz0rcmgYGZA?pwdy7hp 提取码: y7hp 复制这段内容后打开百度网盘手机App,操作更方便哦 --来自百度网盘超级会员v4的分享 课程介绍: 📚【01】Java筑基:全方位指…...

国外服务器怎么有效降低延迟
国外服务器怎么有效降低延迟?在全球化网络环境下,越来越多的企业和个人选择使用国外服务器来托管网站、应用程序或数据。然而,由于地理位置、网络连接等因素,使用国外服务器时可能会遇到延迟较高的问题。高延迟不仅影响用户体验,…...
AI百度文心一言大语言模型接入使用(中国版ChatGPT)
百度文心一言接入使用(中国版ChatGPT) 一、百度文心一言API二、使用步骤1、接口2、请求参数3、请求参数示例4、接口 返回示例 三、 如何获取appKey和uid1、申请appKey:2、获取appKey和uid 四、重要说明 一、百度文心一言API 基于百度文心一言语言大模型…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
