【C语言】什么是结构体内存对齐?结构体的大小怎么计算?

目录
1.结构体内存对齐
对偏移量的理解:
2.结构体的大小计算
2.1结构体中只有普通的数据类型的大小计算
2.2 结构体中有嵌套的结构体的大小计算
3.修改默认对齐数
4.为什么存在内存对齐?
这篇文章主要介绍结构体内存对齐和如何计算大小。
在学习结构体内存对齐之前,不知道大家有没有注意到,当我们有两个结构体,它们的成员变量类型和个数相同,只是顺序不同,当计算它们的大小时,它们的大小不相同,例如下面的代码:
#include<stdio.h>
struct S1
{char c1;int i;char c2;
};
struct S2
{int i;char c1;char c2;
};
int main()
{printf("%d\n", sizeof(struct S1));printf("%d\n", sizeof(struct S2));return 0;
}sizeof计算的大小不相同:

现在,我们就来学习如何计算结构体的大小。
1.结构体内存对齐
结构体内存对齐(Struct Memory Alignment)是指编译器在分配结构体变量的内存空间时,按照一定规则对结构体成员进行排列,以保证结构体的访问效率和内存对齐要求。
在计算结构体的大小之前,我们需要了解结构体的内存对齐规则:
1. 第一个成员在与结构体变量偏移量为0的地址处。
2. 其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。 对齐数 = 编译器默认的一个对齐数与该成员大小的较小值。 VS中默认的值为8,Linux中没有默认对齐数,对齐数就是成员自身的大小
3. 结构体总大小为最大对齐数(每个成员变量都有一个对齐数)的整数倍。
4. 如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
对偏移量的理解:
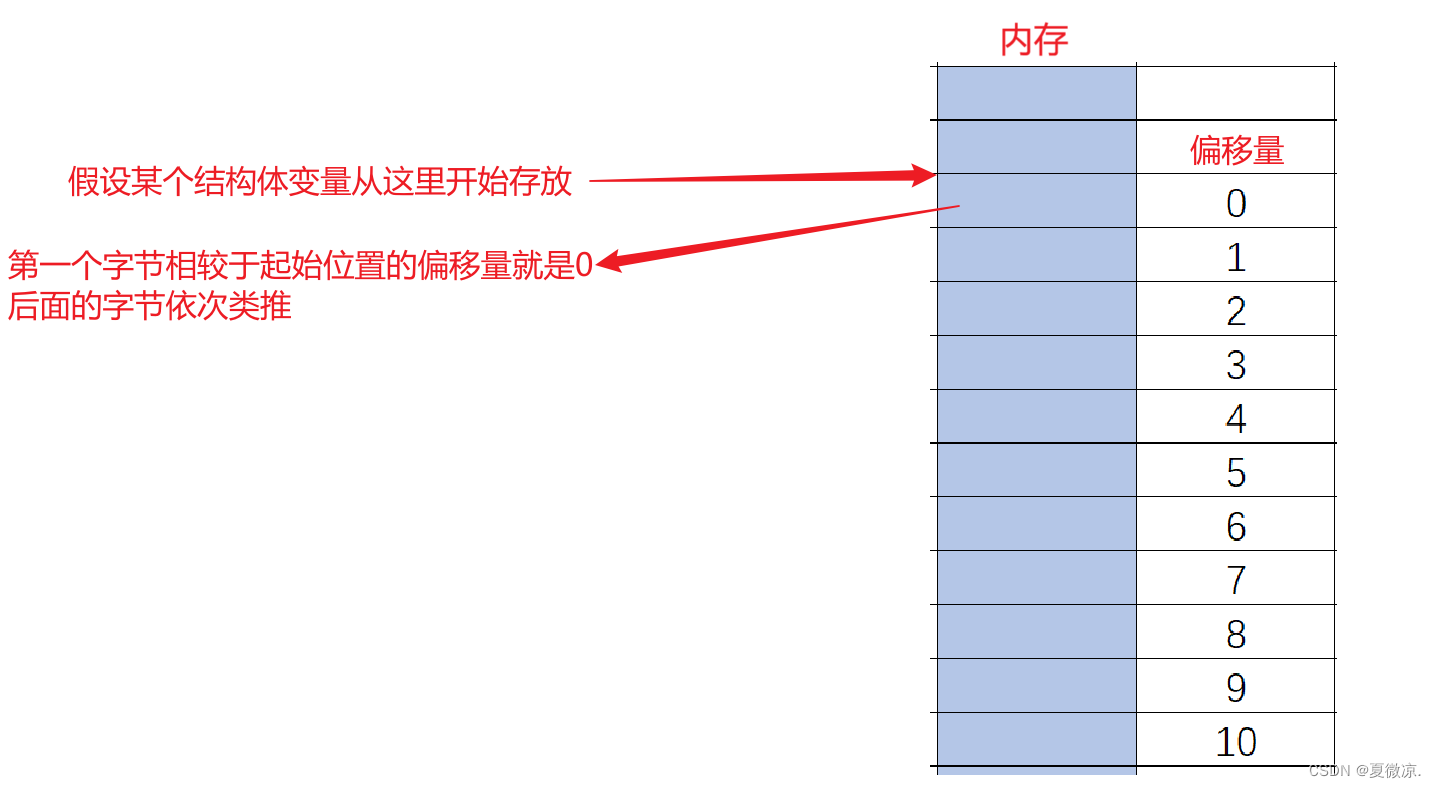
利用 offsetof 可以结算结构体成员变量相较于结构体起始位置的偏移量
#include<stddef.h>
#include<stdio.h>
struct S1
{char c1;int i;char c2;
};
int main()
{printf("%d\n", offsetof(struct S1, c1));printf("%d\n", offsetof(struct S1, i));printf("%d\n", offsetof(struct S1, c2));return 0;
}
根据每个成员变量的偏移量,我们可以结算结构体成员变量在内存中的存储位置:

根据上面的现象分析,我们发现结构体成员不是在内存中连续存放的。
如果想要知道为什么会有浪费掉的空间,我们还得根据结构体的对齐规则继续学习。
2.结构体的大小计算
下面讲解如何根据结构体内存对齐规则来计算结构体的大小:
2.1结构体中只有普通的数据类型的大小计算
还是以这个结构体类型为例:
struct S1
{char c1;int i;char c2;
};
以同样的方法,再来计算下面这个结构体的大小:
struct S2
{int i;char c1;char c2;
};
此时就已经解决了开头的疑问了。
为了巩固学习的知识,再举出一个计算结构体大小的例子:
struct S3
{double d;char c;int i;
};
当结构体中含有数组时,该怎么计算大小呢?
当结构体中有数组类型的变量,我们只需要将数组看作是多个相同类型的变量即可,如下图所示:

编译测试:
2.2 结构体中有嵌套的结构体的大小计算
对于结构体中含有嵌套的结构体,我们就需要使用第4条规则了:
如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整 体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
计算一个试试:
struct S
{double d1;char c1;int i;
};
struct S7
{char c2;struct S s;double d2;
};
int main()
{printf("%d\n", sizeof(struct S7));return 0;
}
3.修改默认对齐数
之前我们见过了 #pragma 这个预处理指令,这里我们再次使用,可以改变我们的默认对齐数。
#pragma pack(8)//设置默认对齐数为8
struct S1
{char c1;int i;char c2;
};
#pragma pack() //取消设置的默认对齐数,还原为默认#pragma pack(1)//设置默认对齐数为1
struct S2
{char c1;int i;char c2;
};
#pragma pack()//取消设置的默认对齐数,还原为默认int main()
{printf("%d\n", sizeof(struct S1));printf("%d\n", sizeof(struct S2));return 0;
}输出结果:
一般情况下,对齐数都是设置成2的次方数,不会随意设置成其他数 。
结论: 结构在对齐方式不合适的时候,我们可以自己更改默认对齐数。
4.为什么存在内存对齐?
大部分的参考资料都是如是说的:
1. 平台原因(移植原因):
不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
2. 性能原因:
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。 原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访 问。
总体来说: 结构体的内存对齐是拿空间来换取时间的做法
拓展:
结构体内存对齐(Struct Memory Alignment)是指编译器在分配结构体变量的内存空间时,按照一定规则对结构体成员进行排列,以保证结构体的访问效率和内存对齐要求。
在计算机中,访问内存的速度是有限的,而且通常是按照特定的字节大小进行的。为了提高内存访问的效率,许多计算机体系结构要求特定类型的数据在内存中的地址必须是某个特定值的倍数。这个特定值通常是数据类型的大小或者是处理器的字长。
结构体内存对齐的目的是为了满足这些对齐要求,以减少内存访问的时间和成本。当结构体的成员变量按照对齐规则进行排列时,可以保证每个成员变量的地址都是对齐的,从而提高内存访问的效率。
具体的对齐规则可能因编译器、操作系统和处理器的不同而有所差异。通常情况下,对齐规则会考虑数据类型的大小和对齐要求,以及结构体成员的顺序和类型。编译器会在结构体的成员之间插入填充字节(Padding Bytes),以保证每个成员的地址满足对齐要求。
需要注意的是,结构体内存对齐可能会导致结构体的大小增加,因为填充字节会占用额外的内存空间。这种增加的大小可能会影响结构体的内存布局和内存占用,特别是在涉及到结构体的嵌套、数组和文件IO等情况下。
在一些特殊情况下,可以使用编译器提供的指令或者属性来控制结构体的内存对齐方式,以满足特定的需求。
那在设计结构体的时候,我们既要满足对齐,又要节省空间,如何做到:
让占用空间小的成员尽量集中在一起。
struct S1
{char c1;int i;char c2;
};
struct S2
{char c1;char c2;int i;
};
S1和S2类型的成员一模一样,但是S1和S2所占空间的大小有了一些区别。

相关文章:

【C语言】什么是结构体内存对齐?结构体的大小怎么计算?
目录 1.结构体内存对齐 对偏移量的理解: 2.结构体的大小计算 2.1结构体中只有普通的数据类型的大小计算 2.2 结构体中有嵌套的结构体的大小计算 3.修改默认对齐数 4.为什么存在内存对齐? 这篇文章主要介绍结构体内存对齐和如何计算大小。 在学习结构体内存…...

【Redis】Redis中的布隆过滤器
【Redis】Redis中的布隆过滤器 前言 在实际开发中,会遇到很多要判断一个元素是否在某个集合中的业务场景,类似于垃圾邮件的识别,恶意IP地址的访问,缓存穿透等情况。类似于缓存穿透这种情况,有许多的解决方法…...

接口测试 —— Jmeter 参数加密实现
Jmeter有两种方法可以实现算法加密 1、使用__digest自带函数 参数说明: Digest algorithm:算法摘要,可输入值:MD2、MD5、SHA-1、SHA-224、SHA-256、SHA-384、SHA-512 String to be hashed:要加密的数据 Salt to be…...

Linux c语言字节序
文章目录 一、简介二、大小端判断2.1 联合体2.2 指针2.3 网络字节序 一、简介 字节序(Byte Order)指的是在存储和表示多字节数据类型(如整数和浮点数)时,字节的排列顺序。常见的字节序有大端字节序(Big En…...

批量将excel中第5列中内容将人名和电话号码进行分列
使用Python可以使用openpyxl库来实现批量将Excel中第5列的内容分列为人名和电话号码的操作。下面是示例代码: import openpyxl def split_names_and_phone_numbers(file_path, sheet_name): # 加载Excel文件 workbook openpyxl.load_workbook(file_path) …...

WPF DataGrid columns表头根据数据集动态动态生成Demo
思路是这样的,数组集合装表头的信息,遍历这个集合,遍历过程中处理一下数据,然后就把每表头信息添加到dataGrid2.Columns.Add(templateColumn); 1,页面Xaml代码: <DataGrid x:Name"dataGrid" …...
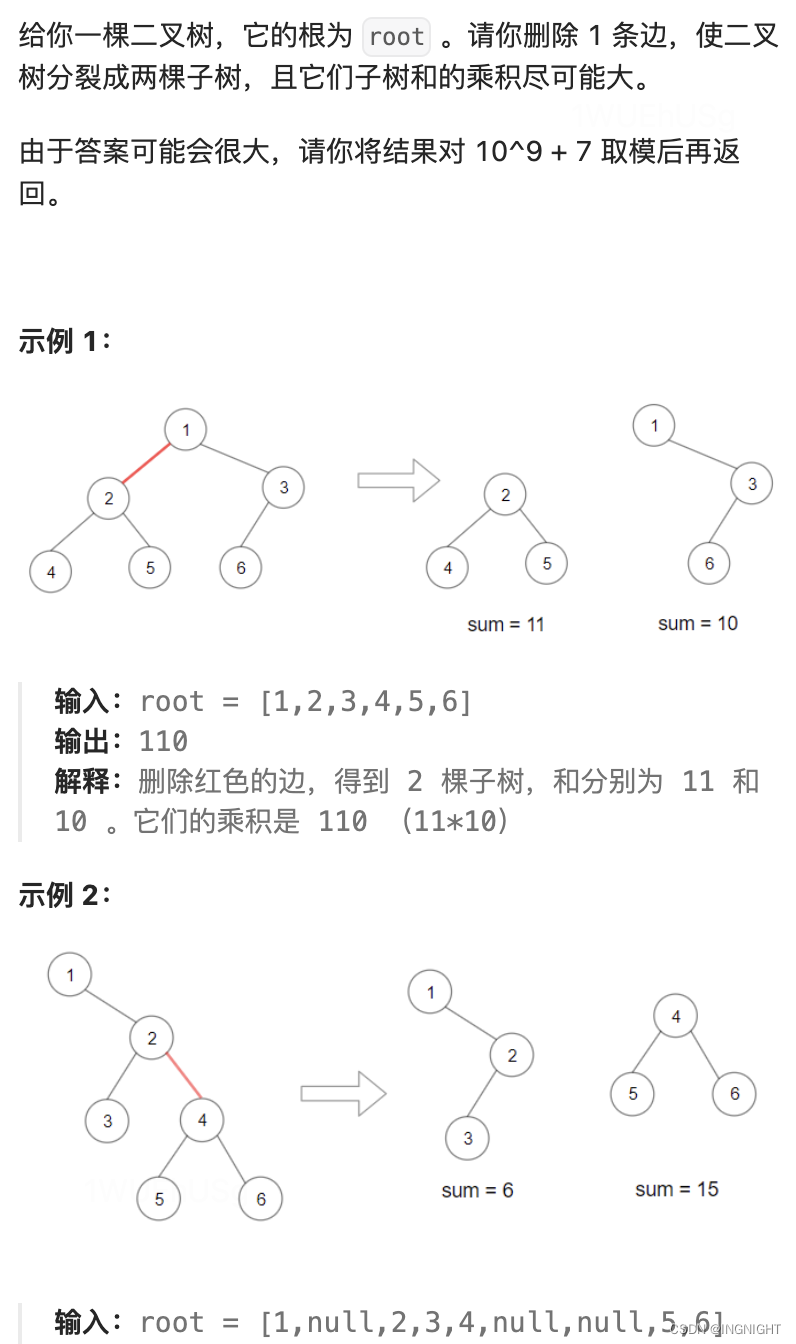
1339. 分裂二叉树的最大乘积
链接: 1339. 分裂二叉树的最大乘积 题解: /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* …...

【C++】Stack和Queue
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析3 目录 👉🏻Stack Constructor👉🏻Stack …...

Maven之tomcat7-maven-plugin 版本低的问题
tomcat7-maven-plugin 版本『低』的问题 相较于当前最新版的 tomcat 10 而言,tomcat7-maven-plugin 确实看起来很显老旧。但是,这个问题并不是问题,至少不是大问题。 原因 1:tomcat7-maven-plugin 仅用于我们(程序员&…...
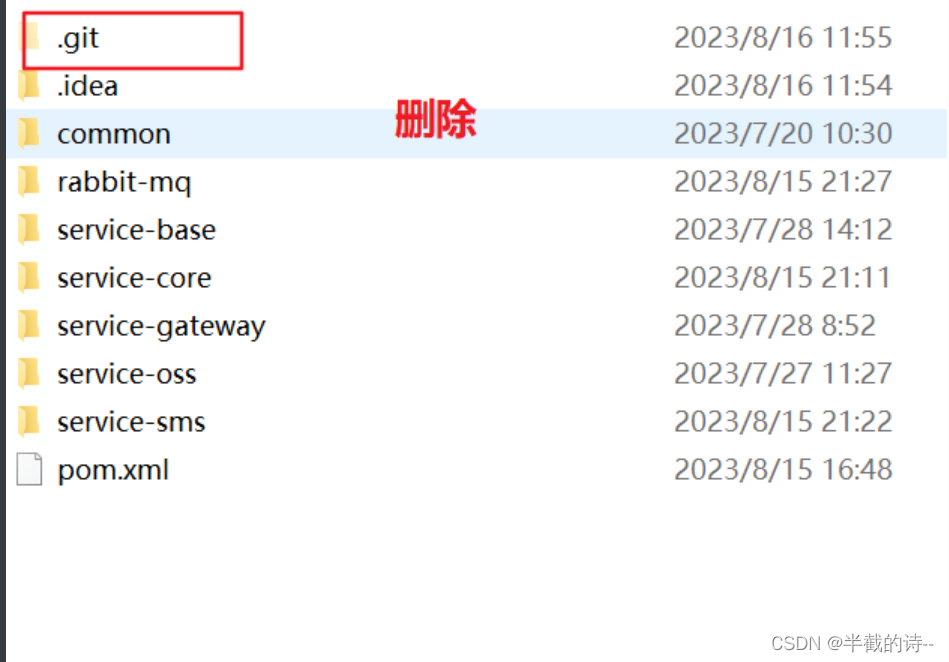
在项目中如何解除idea和Git的绑定
在项目中如何解除idea和Git的绑定 1、点击File--->Settings...(CtrlAltS)--->Version Control--->Directory Mappings--->点击取消Git的注册根路径: 2、回到idea界面就没有Git了: 3、给这个项目初始化 这样就可以重新绑定远程仓库了&#x…...
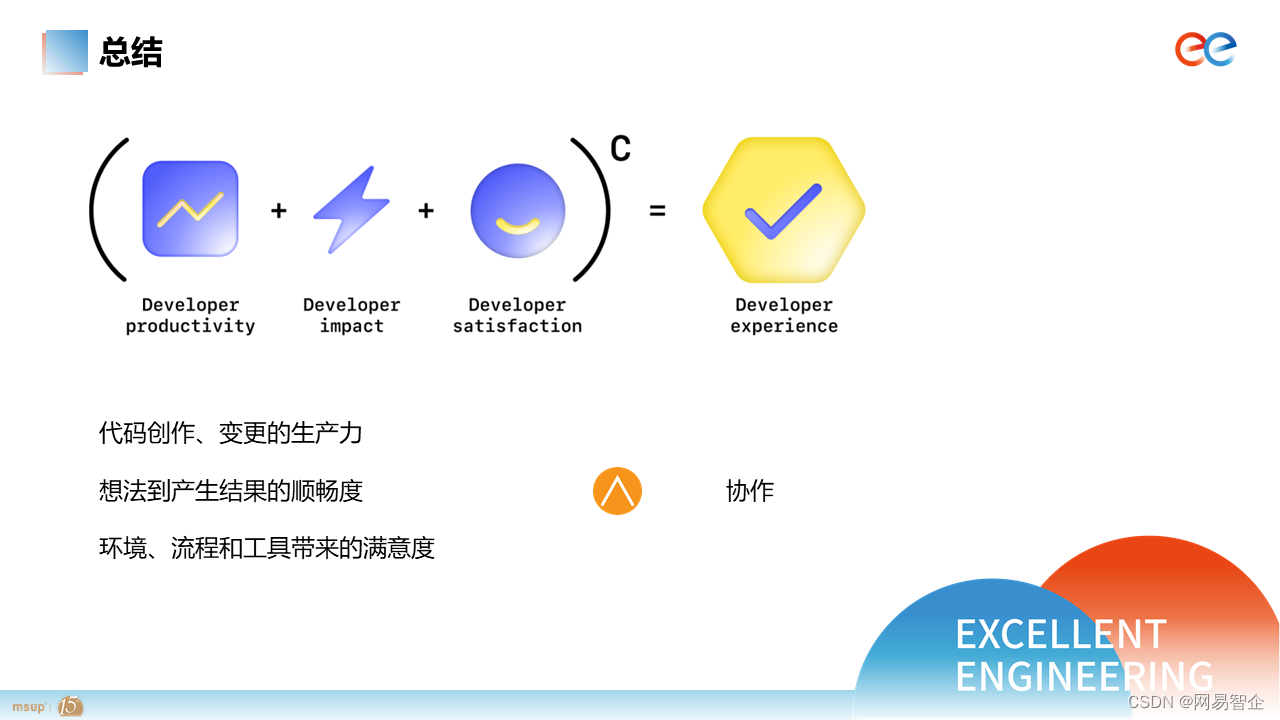
AGI 在网易云信的技术提效和业务创新
We believe our research will eventually lead to artificial general intelligence, a system that can solve human-level problems. Building safe and beneficial AGI is our mission. ---- OpenAI 通用人工智能 AGI 作为 AI 的终极形态,是 AI 行业内追求的演…...

线性代数的学习和整理9(草稿-----未完成)
3.3 特征值和特征向量是什么? 直接说现在:特征向量这个块往哪个方向进行了拉伸,各个方向拉伸了几倍。这也让人很容易理解为什么,行列式的值就是特征值的乘积。 特征向量也代表了一些良好的性质,即这些线在线性变换后…...

React的useReducer与Reudx对比
useReducer 和 Redux 都是用于处理应用程序的状态管理的工具,但它们在概念和使用场景上存在一些区别。 useReducer: useReducer 是 React 提供的一个 Hook,用于管理局部状态。它接受一个 reducer 函数和初始状态,并返回一个包含当…...
深度学习环境搭建 cuda、模型量化bitsandbytes安装教程 windows、linux
cuda、cudann、conda安装教程 输入以下命令,查看 GPU 支持的最高 CUDA 版本。 nvidia-smi cuda安装(cudatoolkit) 前往 Nvidia 的 CUDA 官网:CUDA Toolkit Archive | NVIDIA Developer CUDA Toolkit 11.8 Downloads | NVIDIA …...

pythond assert 0 <= colx < X12_MAX_COLS AssertionError
python使用xlrd读取excel时,报错: assert 0 < colx < X12_MAX_COLS AssertionError 大意是excel列太多了。主要是xlrd库的问题。最好的方法是不用它,但是我用的其他人提供的工具用到它,没法改。 尝试手动删除excel的列&am…...
js简介以及在html中的2种使用方式(hello world)
简介 javascript :是一个跨平台的脚本语言;是一种轻量级的编程语言。 JavaScript 是 Web 的编程语言。所有现代的 HTML 页面都使用 JavaScript。 HTML: 结构 css: 表现 JS: 行为 HTMLCSS 只能称之为静态网页࿰…...

vsCode使用cuda
一、vsCode使用cuda 前情提要:配置好mingw: 1.安装cuda 参考: **CUDA Toolkit安装教程(Windows):**https://blog.csdn.net/qq_42951560/article/details/116131410 2.在vscode中添加includePath c_cp…...

ubuntu无法使用apt命令时怎么安装库
如题 因为某些原因,不能直接联网使用apt命令安装库。只能手动去ubuntu镜像源里 找对应的包的deb安装文件 镜像源地址(适用于AMD64架构,就是常见的PC的X86-64啦) 镜像源地址(适用于ARM64,armhf,ppc64el,riscv64,s390x架构ÿ…...

防火墙firewall
一、什么是防火墙 二、iptables 1、iptables介绍 2、实验 138的已经被拒绝,1可以 三、firewalld 1、firewalld简介 关闭iptables,开启firewalld,curl不能使用,远程连接ssh可以使用 添加80端口 这样写也可以:添加http…...

拿来即用,自己封装的 axios
文章目录 一、需求二、分析1. 安装axios2. 新建一个 ts 文件,封装 axios3. store 存放 token 信息4. 使用5. 文件 type.js 一、需求 在日常开发中,我们会经常用到 axios ,那么如何在自己的项目中自己封装 axios 二、分析 1. 安装axios np…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
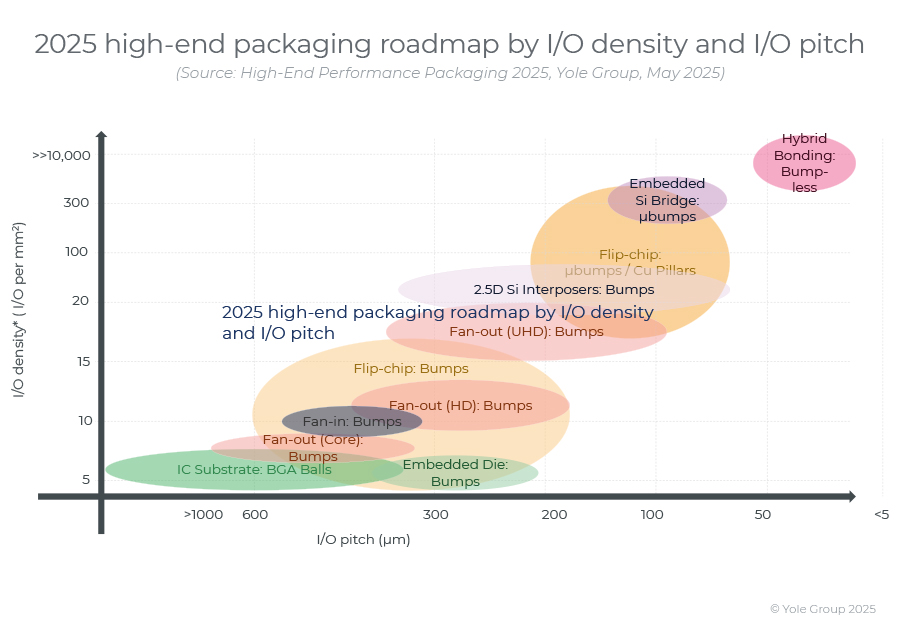
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...

