C++11 std::async推荐使用 std::launch::async 模式
async真假多线程
std::launch::async真多线程
std::launch::async | std::launch::deferred可能多线程
std::launch::deferred假多线程
枚举变量说明
枚举定义
enum class launch
{async = 1, // 0b1deferred = 2, // 0b10any = async | deferred // 0b11
};
std::launch::async: 一定在另一个线程跑函数
std::launch::deferred: get,wait代码所在线程跑函数;
即调用get,wait的时候再串行执行函数; 如果不调用则不执行;
默认: any
即默认可能延迟, 也可能立即执行; 跟系统当时的负载均衡, 超限等方面的阈值决定, 采取延迟还是立即执行;
默认机制的问题std::launch::any
案例
void t() {auto fut = std::async(f); // run f using default launch policy
}
问题: 不确定性
f, t可能在一个线程执行, 也可能在不同的线程执行;fut.get|fut.wait, f这两个也可能在一个线程, 也可能不在一个线程;f可能在执行, 可能不在执行;
影响数据: TLS:thread local storage
thread_local修饰的可能会新创建, 也可能不创建; 就有很大的问题;
影响逻辑: wait问题
auto fut = std::async(f);while (fut.wait_for(100ms) != std::future_status::ready) {
}
enum class future_status {ready,timeout,deferred
};
f可能永远也没有执行; fut的状态永远是deferred; 永远循环下去;
这种可能漏洞可能永远也不会触发, 因为即使是压测或其他测试, 测试环境可能永远也不会出现; 但是在一些极端环境就啃根出现;
影响逻辑: 规避方案
wait_for(0)状态查询;
auto fut = std::async(f);if (fut.wait_for(0) != std::future_status::deferred) {// do something and return;// ...use wait or get on fut to call f synchronously
} else {while (fut.wait_for(100ms) != std::future_status::deferred) {// task is neither deferred nor ready, so do concurrent work until it's ready}// now is ready.
}
default使用条件
f不用和get,wait调用者所在线程并行;- 不关注
thread_local变量的线程安全; - 接受函数执行和不执行的代价; 接受
get,wait时阻塞执行; 接受不调用get, wait不执行; - 考虑到了延迟执行的情况和代价;
一定多线程
std::launch::async
auto fut = std::async(std::launch::async, f);
默认std::launch::async: c++11
template<typename F, typename... Ts>
inline
std::future<typename std::result_of<F(Ts...)>::type>
reallyAsync(F&& f, Ts&&... params) // return future
{// for asynchronous // call to f(params...)return std::async(std::launch::async,std::forward<F>(f), std::forward<Ts> (params)...);
}默认std::launch::async: c++14
template<typename F, typename... Ts>
inline
auto
reallyAsync(F&& f, Ts&&... params) // return future
{// for asynchronous // call to f(params...)return std::async(std::launch::async,std::forward<F>(f), std::forward<Ts> (params)...);
}
差异: c++11不支持返回值类型推理;
总结
默认: deferred + async的结合, 行为未知, 大多数异步;
默认影响: thread_local, 任务不执行, wait无限等待;
std::launch::async强制多线程;
相关文章:

C++11 std::async推荐使用 std::launch::async 模式
async真假多线程 std::launch::async真多线程 std::launch::async | std::launch::deferred可能多线程 std::launch::deferred假多线程 枚举变量说明 枚举定义 enum class launch {async 1, // 0b1deferred 2, // 0b10any async | def…...

没有使用springboot 单独使用spring-boot-starter-logging
如果您不使用Spring Boot框架,但想单独使用Spring Boot Starter Logging,您可以按照以下步骤进行: 1. 添加Maven依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boo…...

创建Azure资源锁
锁的介绍 在Azure中,资源锁是一种用于保护订阅、资源组或者单个资源的机制。它可以防止对受锁定的资源进行删除或修改操作,帮助确保资源的连续可用性和安全性。 Azure中的资源锁可以分为两种类型: 删除锁(CanNotDelete…...
 – 使用 TensorFlow 在 Python 中开发图像分类器)
卷积神经网络教程 (CNN) – 使用 TensorFlow 在 Python 中开发图像分类器
在这篇博客中,让我们讨论什么是卷积神经网络 (CNN) 以及 卷积神经网络背后的架构——旨在解决 图像识别系统和分类问题。 卷积神经网络在图像和视频识别、推荐系统和自然语言处理方面有着广泛的应用。 目录 计算机如何读取图像? 为什么不是全连接网络?...

MyBatis XML映射处理CLOB和BLOB类型
Mybatis的MapperXML映射文件应该处理数据库字段类型为CLOB和BLOB类型的数据呢?首先我们先看下CLOB和BLOB这两种数据类型的介绍。 介绍 使用Mybatis时涉及到两种特殊类型的处理,分别是Blob(Binary Large Object)和Clob࿰…...

FPGA_学习_14_第一个自写模块的感悟和ila在线调试教程与技巧(寻找APD的击穿偏压)
前一篇博客我们提到了,如果要使用算法找到Vbr,通过寻找APD采集信号的噪声方差的剧变点去寻找Vbr是一个不错的方式。此功能的第一步是在FPGA中实现方差的计算,这个我们已经在上一篇博客中实现了。 继上一篇博客之后,感觉过了很久了…...

【2023新教程】树莓派定时自动拍照并上传腾讯云对象存储COS
1 换源 仅适用于Release date: May 3rd 2023、Debian version: 11 (bullseye)这个树莓派OS版本,其他版本不保证有效。 首先使用如下命令,查看自己树莓派的架构。 uname -a结果如下: 如果红圈处显示为aarch64,使用命令sudo na…...

校企合作谋发展 合作共赢谱新篇|云畅科技与湖南民族职业学院签订校企合作协议
产业是经济发展的重要引擎,人才是产业发展的重要资源。为积极探索软件人才培育新路径,共商政产学研协同新机制,8月8日,云畅科技与湖南省民族职业学院教育技术学院软件技术专业签订校企合作协议。 会上,学院副校长王志平…...
vue技术学习
vue快速入门 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>vue快速入门</title> </head> <body> <!--老师解读 1. div元素不是必须的,也可以是其它元素࿰…...
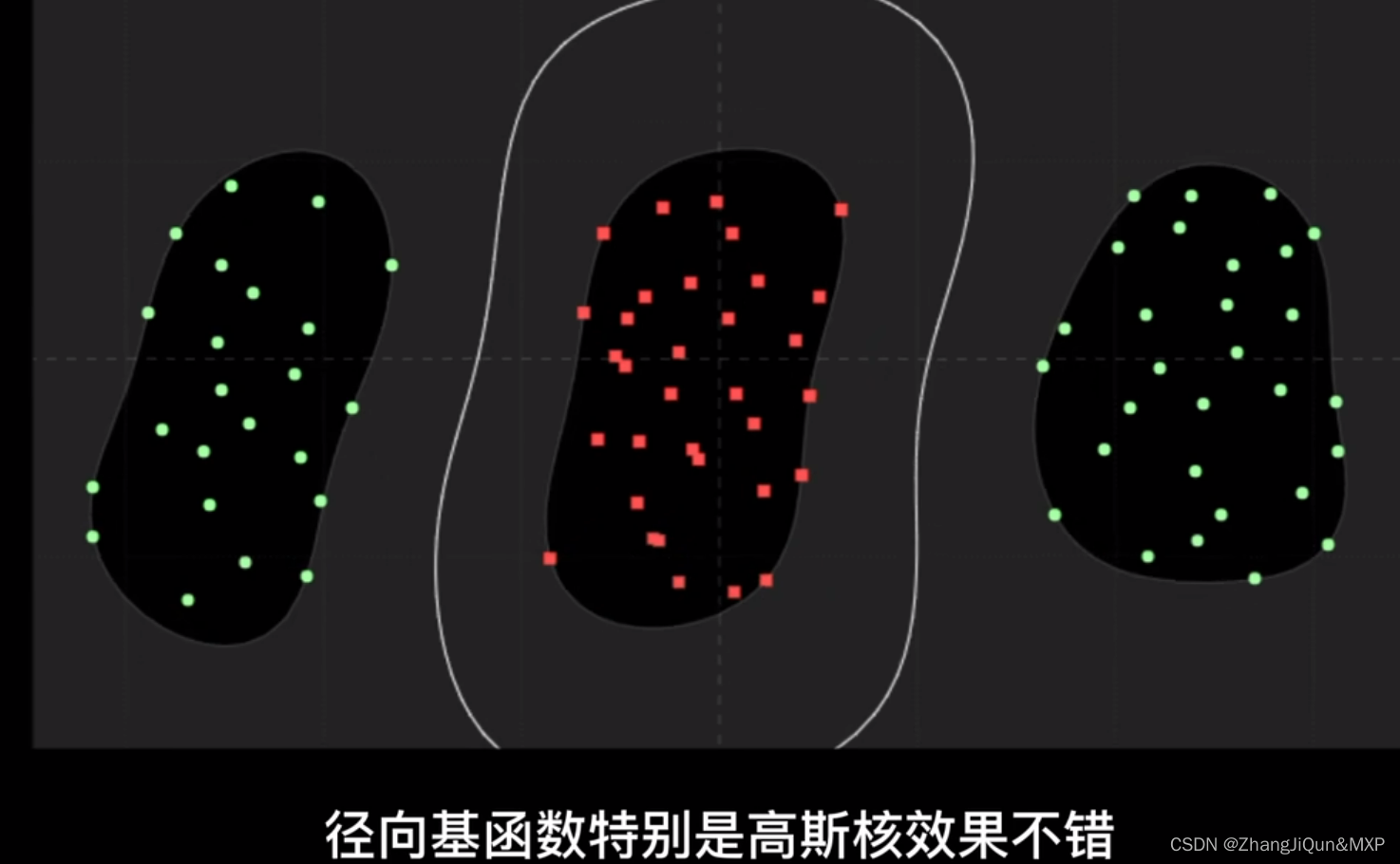
基于空间的图卷积神经网络:GNN
目录 欧氏空间中神经网络发挥巨大最作用,DNA,知识图谱三维或者多维空间不行 邻接矩阵实现图结构的矩阵化表示:造梦师 局和操作实现层内消息传递:带线的连接机传递消息 GCN通过邻域聚合实现特征提取 SVM支持向量机 编辑 硬分…...

.net core发布到IIS上出现 HTTP 错误 500.19
1.检查.net core 环境运行环境是否安装完成,类似如下环境 2.IIS是否安装全 本次原因就是IIS未安装全导致的 按照网上说的手动重启iis(iisreset)也不行...

01_Redis单线程与多线程
01——Redis单线程与多线程 一、Redis是单线程还是多线程 在谈Redis的单线程或多线程时,需要根据版本来区分。 在redis 3.x之前,redis是单线程的从redis 4.x开始,redis引入多线程。处理客户端请求时,使用单线程;在异…...

机器学习——随机森林【手动代码】
随机森林这个内容,是目前来说。。。最最最简单,最好理解,应该也是最好实现的了!!! 先挖坑,慢慢填 随机森林,这个名字取得,果然深得该算法的核心精髓,既随机&a…...

Vue 2 处理边界情况
访问元素和组件 通过Vue 2 组件基础一文的学习,我们知道组件之间可以通过传递props或事件来进行通信。 但在一些情况下,我们使用下面的方法将更有用。 1.访问根实例 根实例可通过this.$root获取。 我们在所有子组件中都可以像上面那样访问根实例&…...

写一个mysql 正则表达式,每三个img标签图片后面添加<hr>
你可以使用MySQL的REGEXP_REPLACE函数来实现这个需求。下面是一个示例的正则表达式和SQL语句: sql UPDATE your_table SET your_column REGEXP_REPLACE(your_column, (<img[^>]*>){3}, $0<hr>) WHERE your_column REGEXP (<img[^>]*>){3}…...
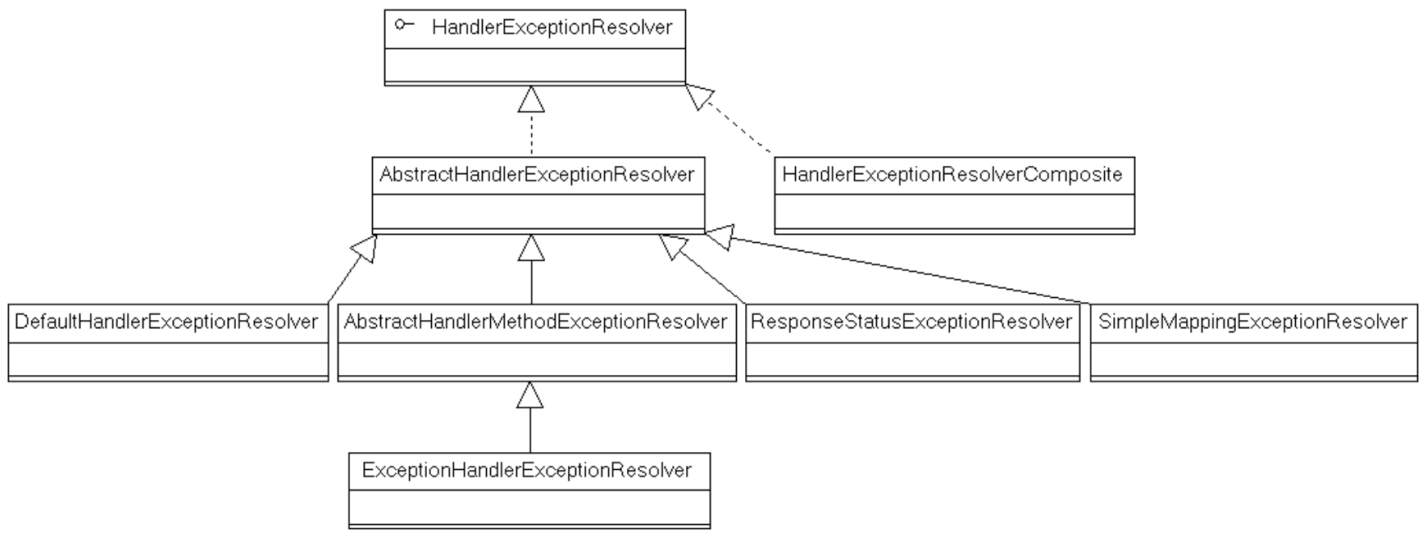
Spring MVC异常处理
Spring MVC异常处理 Spring MVC异常处理机制HandlerExceptionResolver的实现类DefaultHandlerExceptionResolver实现类DefaultHandlerExceptionResolver 在Controller的请求处理方法中手动使用try…catch块捕捉异常,当捕捉到指定的异常时,系统返回对应的…...

Centos7安装docker后默认开启docker0的网卡|卸载默认网卡
docker实战(一):centos7 yum安装docker docker实战(二):基础命令篇 docker实战(三):docker网络模式(超详细) docker实战(四):docker架构原理 docker实战(五):docker镜像及仓库配置 docker实战(六):docker 网络及数据卷设置 docker实战(七):docker 性质及版本选择 认知升…...
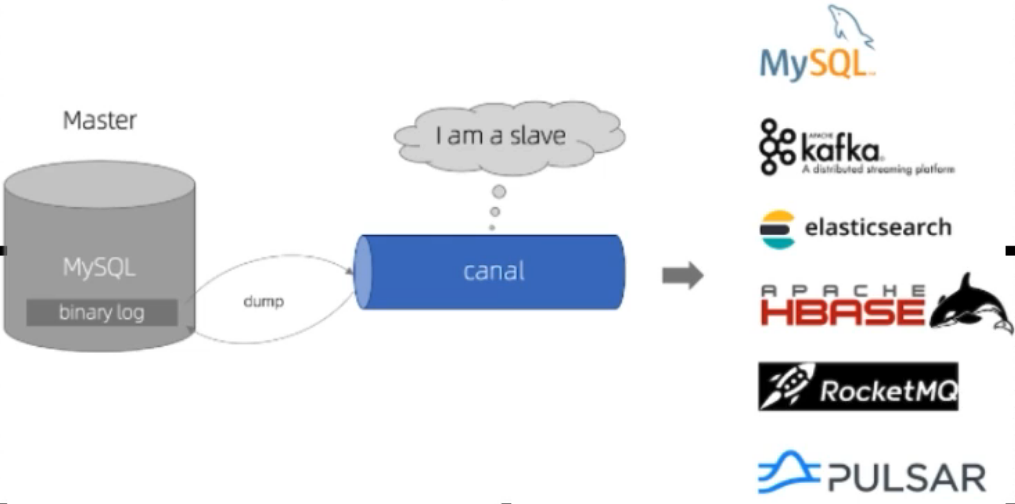
04_Redis与mysql数据双写一致性案例
04——redis与mysql数据双写一致性 一、canal 是什么 canal[ka’nel,中文翻译为水道/管道/沟渠/运河,主要用途是用于MySQL数据库增量日志数据的订阅、消费和解析,是阿里巴巴开发并开源的,采用Java语言开发; 历史背景是早期阿里巴巴因为杭州和…...

vue的开发者工具下载『保姆级别』
1.先进官网 极简插件_Chrome扩展插件商店_优质crx应用下载 (zzzmh.cn) 2.搜索vue devtools,点击进去 3.下载插件 4.下载到文件下你自己的文件下:我的是下载到E盘下。 5.压缩到当前目录下 6.电脑进入拓展程序(不同的浏览器操作不同ÿ…...
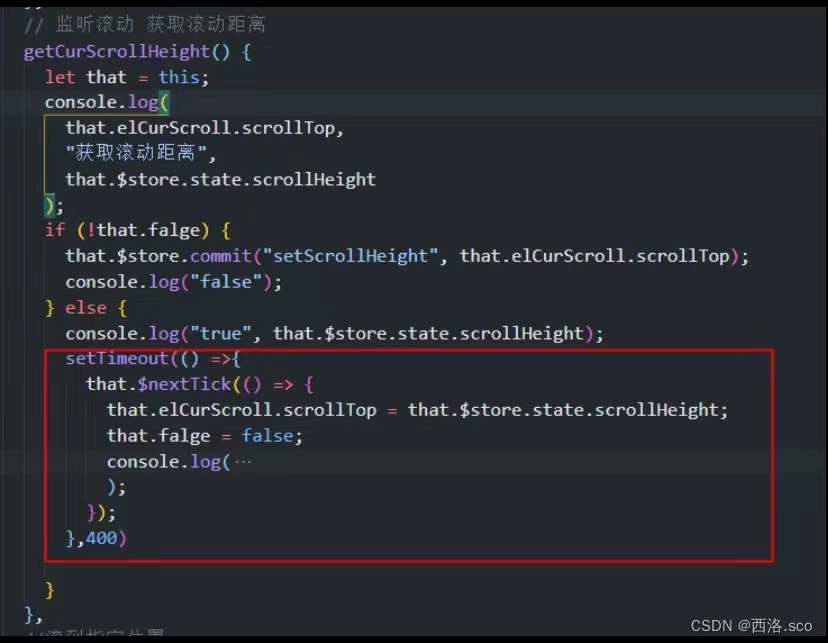
vue的scrollTop手机环境设置值失效,本地正常可以赋值
获取div盒子ref或者document获取都行 监听方法 一定要加this.$nexttick,在本地测试只用nexttick是没有问题的,但是到手机测试就不行了,原因是因为手机渲染比本地更快,所以结合setTimeout使用 如果有更好的处理方法,恳请大佬指点一…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
