85-最大矩阵
题目
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
示例 3:
输入:matrix = [[“0”]]
输出:0
示例 4:
输入:matrix = [[“1”]]
输出:1
示例 5:
输入:matrix = [[“0”,“0”]]
输出:0
思路
最大矩形面积问题可以使用栈来解决,结合柱状图的特性。下面我将详细解释解题思路,并提供关键算法和算法思想的说明。
解题思路:
对于每一行,我们可以将每个元素的值视为当前位置向上的高度。我们可以根据每一行的高度构建一个柱状图,然后使用栈来计算柱状图中的最大矩形面积。
-
对于每一行,我们构建一个高度数组
heights,其中heights[j]表示从当前行的第j列向上的连续 1 的数量。我们可以根据上一行的高度数组和当前行的元素来更新这个数组。 -
对于
heights数组,我们使用栈来辅助计算最大矩形面积。我们遍历heights数组,如果当前高度大于栈顶高度,就将当前索引入栈。否则,我们弹出栈顶索引,并计算以该高度为高的矩形面积,宽度为当前索引与弹出索引之间的距离。我们不断更新最大面积,直到栈为空或者当前高度大于栈顶高度。
关键算法和算法思想:
栈是解决这个问题的关键算法思想。通过使用栈,我们可以维护一个递增的高度序列,当遇到下降的高度时,我们可以计算以当前高度为高的矩形面积,利用栈中保存的索引信息。
代码
object Solution {def maximalRectangle(matrix: Array[Array[Char]]): Int = {if (matrix.isEmpty) return 0val rows = matrix.lengthval cols = matrix(0).lengthvar maxArea = 0val heights = Array.fill(cols)(0)def largestRectangleArea(heights: Array[Int]): Int = {val stack = collection.mutable.Stack[Int]()var maxArea = 0for (i <- 0 until heights.length) {while (stack.nonEmpty && heights(i) < heights(stack.top)) {val height = heights(stack.pop())val width = if (stack.isEmpty) i else i - stack.top - 1maxArea = math.max(maxArea, height * width)}stack.push(i)}while (stack.nonEmpty) {val height = heights(stack.pop())val width = if (stack.isEmpty) heights.length else heights.length - stack.top - 1maxArea = math.max(maxArea, height * width)}maxArea}for (i <- 0 until rows) {for (j <- 0 until cols) {if (matrix(i)(j) == '1') heights(j) += 1else heights(j) = 0}maxArea = math.max(maxArea, largestRectangleArea(heights))}maxArea}
}// 示例
val matrix = Array(Array('1','0','1','0','0'),Array('1','0','1','1','1'),Array('1','1','1','1','1'),Array('1','0','0','1','0')
)
val result = Solution.maximalRectangle(matrix)
println(result) // 输出:6
相关文章:

85-最大矩阵
题目 给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。 示例 1: 输入:matrix [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,…...

8.3 【C语言】通过指针引用数组
8.3.1 数组元素的指针 所谓数组元素的指针就是数组元素的地址。 可以用一个指针变量指向一个数组元素。例如: int a[10]{1,3,5,7,9,11,13,15,17,19}; int *p; p&a[0]; 引用数组元素可以用下标法,也可以用指针法…...

基于Flink CDC实时同步PostgreSQL与Tidb【Flink SQL Client模式下亲测可行,详细教程】
文章目录 一、PostgreSQL作为数据来源(source),由flink读取1.postgre安装与配置2.flink安装与配置3.flink cdc postgre配置3.1 postgre配置(for flink cdc)3.2 flink cdc postgres的jar包下载 4.flink cdc postgre测试…...
Vue-5.编译器Idea
Vue专栏(帮助你搭建一个优秀的Vue架子) Vue-1.零基础学习Vue Vue-2.Nodejs的介绍和安装 Vue-3.Vue简介 Vue-4.编译器VsCode Vue-5.编译器Idea Vue-6.编译器webstorm Vue-7.命令创建Vue项目 Vue-8.Vue项目配置详解 Vue-9.集成(.editorconfig、…...

qiuzhiji3
本篇想介绍一下慧与,这里的工作氛围和企业文化令人难忘,希望更多人了解它 也想探讨一下不同的文化铸就的不同企业,究竟有哪些差别。 本篇将从我个人角度出发描述慧与。 2022/3/16至2023/7/31 本篇初次写于2023年8月20日 说起来在毕业之前那段…...
JVM——垃圾回收(垃圾回收算法+分代垃圾回收+垃圾回收器)
1.如何判断对象可以回收 1.1引用计数法 只要一个对象被其他对象所引用,就要让该对象的技术加1,某个对象不再引用其,则让它计数减1。当计数变为0时就可以作为垃圾被回收。 有一个弊端叫做循环引用,两个的引用计数都是1ÿ…...

QT TLS initialization failed问题(已解决) QT基础入门【网络编程】openssl
问题: qt.network.ssl: QSslSocket::connectToHostEncrypted: TLS initialization failed 这个问题的出现主要是使用了https请求:HTTPS ≈ HTTP + SSL,即有了加密层的HTTP 所以Qt 组件库需要OpenSSL dll 文件支持HTTPS 解决: 1.加入以下两行代码获取QT是否支持opensll以…...

SpringMVC之获取请求参数
文章目录 前言一、通过ServletAPI获取二、通过控制器方法的形参获取请求参数三、注解1.RequestParam2.RequestHeader3.CookieValue前面的代码总和:4.通过POJO获取请求参数 三、解决获取请求参数的乱码问题总结 前言 下面用到了thymeleaf,不知道的可以看…...
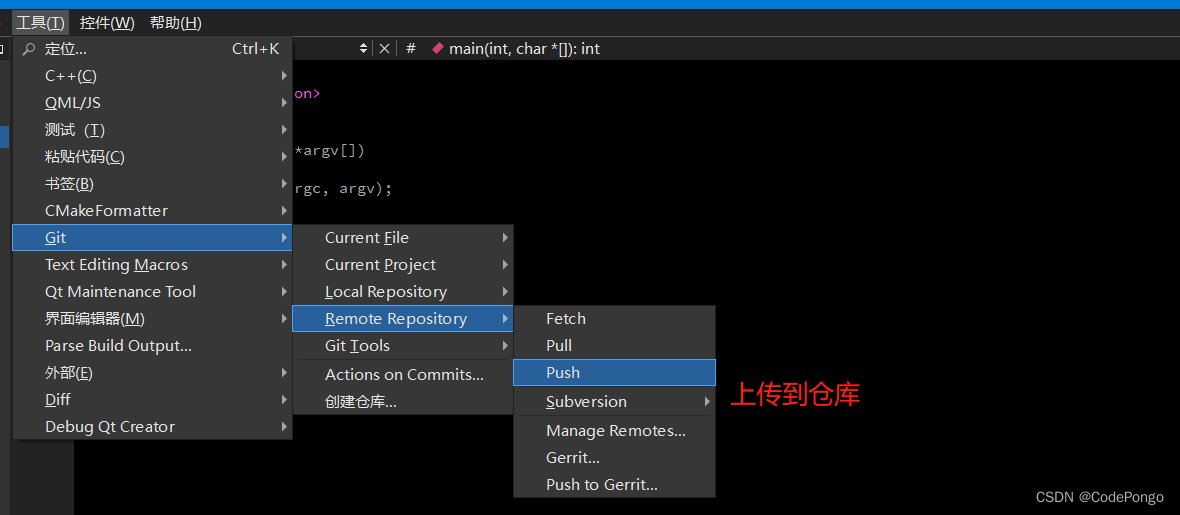
【无标题】QT应用编程: QtCreator配置Git版本控制(码云)
QT应用编程: QtCreator配置Git版本控制(码云) 感谢:DS小龙哥的文章,这篇主要参考小龙哥的内容。 https://cloud.tencent.com/developer/article/1930531?areaSource102001.15&traceIdW2mKALltGu5f8-HOI8fsN Qt Creater 自带了git支持。但是一直没…...

JVM面试题-2
1、有哪几种垃圾回收器,各自的优缺点是什么? 垃圾回收器主要分为以下几种:Serial、ParNew、Parallel Scavenge、Serial Old、Parallel Old、CMS、G1; Serial:单线程的收集器,收集垃圾时,必须stop the worl…...
kafka安装说明以及在项目中使用
一、window 安装 1.1、下载安装包 下载kafka 地址,其中官方版内置zk, kafka_2.12-3.4.0.tgz其中这个名称的意思是 kafka3.4.0 版本 ,所用语言 scala 版本为 2.12 1.2、安装配置 1、解压刚刚下载的配置文件,解压后如下&#x…...
二叉树搜索
✅<1>主页:我的代码爱吃辣📃<2>知识讲解:数据结构——二叉搜索树☂️<3>开发环境 :Visual Studio 2022💬<4>前言:在之前的我们已经学过了普通二叉树,了解了基本的二叉树…...
【先进PID控制算法(ADRC,TD,ESO)加入永磁同步电机发电控制仿真模型研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
k8s集群生产环境的问题处理
2 k8s上的服务均无法访问 执行命令kubectl get pods -ALL,k8s集群中的服务均是running状态 1 kuboard 网页无法访问 kuboard无法通过浏览器访问,但是查看端口是被占用的...
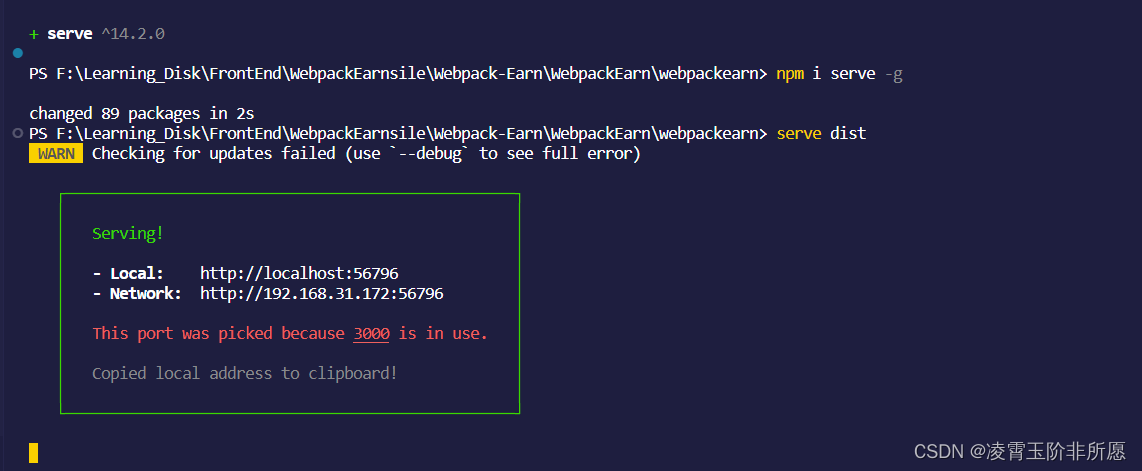
serve : 无法将“serve”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。
1、在学习webpack打包的时候,需要 serve用来启动开发服务器来部署代码查看效果的。安装完之后运行出现以下错误: 2、使用命令查看安装目录: npm list -g我们已经安装过了 3、解决: 我们看到上图路径在:C:\Users\qiy…...
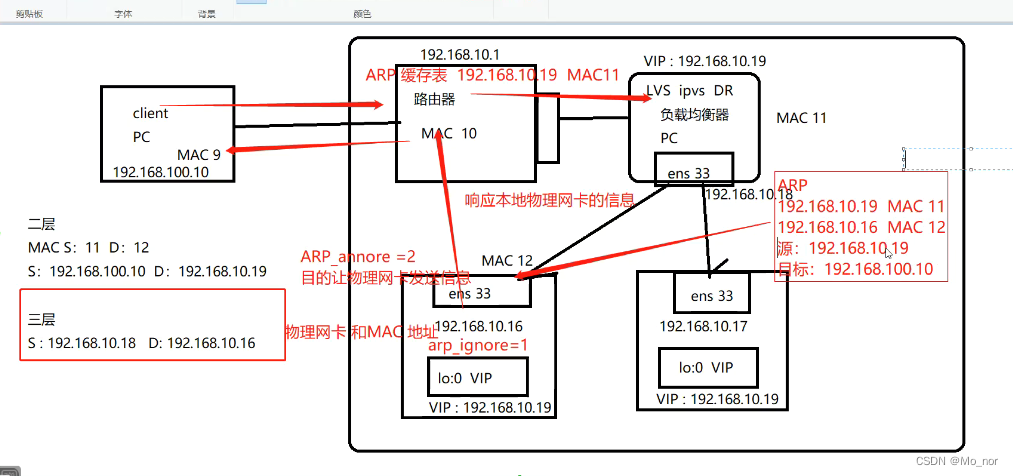
【LVS】2、部署LVS-DR群集
LVS-DR数据包的流向分析 1.客户端发送请求到负载均衡器,请求的数据报文到达内核空间; 2.负载均衡服务器和正式服务器在同一个网络中,数据通过二层数据链路层来传输; 3.内核空间判断数据包的目标IP是本机VIP,此时IP虚…...
)
设计模式 -- 单例模式(传统面向对象与JavaScript 的对比实现)
单例模式 – 传统面向对象与JavaScript 的对比实现 文章目录 单例模式 -- 传统面向对象与JavaScript 的对比实现传统的面向对象的实现定义实现思路初级实现缺点 透明的单例模式实现目的(实现效果)实现缺点 用代理实现单例模式优点 JavaScript 中的单例模…...
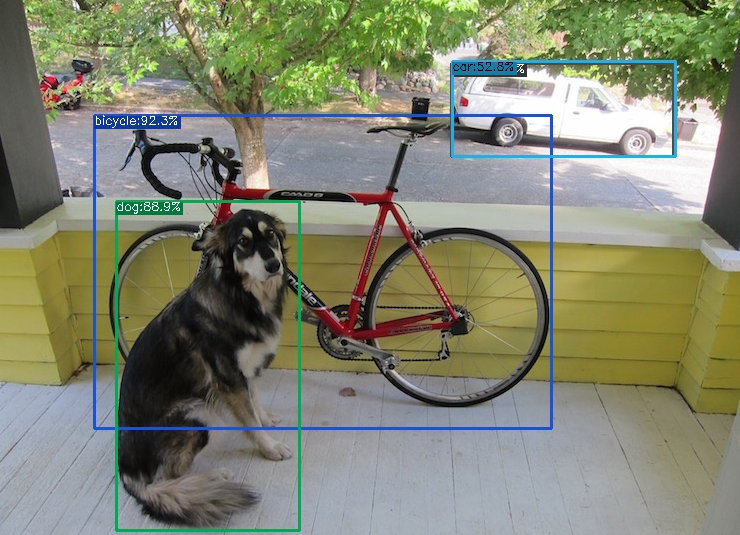
YOLOX算法调试记录
YOLOX是在YOLOv3基础上改进而来,具有与YOLOv5相媲美的性能,其模型结构如下: 由于博主只是要用YOLOX做对比试验,因此并不需要对模型的结构太过了解。 先前博主调试过YOLOv5,YOLOv7,YOLOv8,相比而言,YOLOX的环…...
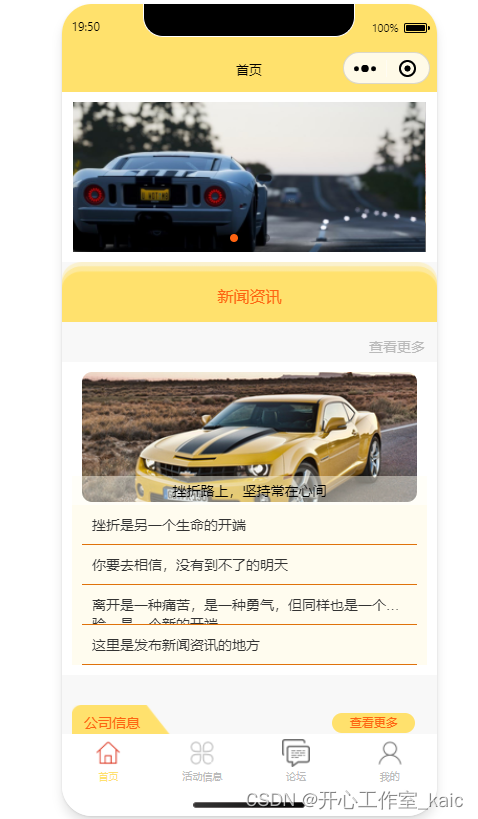
基于小程序的汽车俱乐部系统的设计与实现(论文+源码)_kaic
目录 前 言 1 系统概述 1.1 系统主要功能 1.2 开发及运行环境 2 系统分析和总体设计 2.1 需求分析 2.2 可行性分析 2.3 设计目标 2.4 项目规划 2.5 系统开发语言简介 2.6 系统功能模块图 3 系统数据库设计 3.1 数据库开发工具简介 3.2 数据库需求分析 3.3 数据库…...

ProgrammingArduino物联网
programming_arduino_ed2 IO 延时闪灯 void setup() {pinMode(13, OUTPUT); }void loop() {digitalWrite(13, HIGH);delay(500);digitalWrite(13, LOW);delay(500); }// sketch 03-02 加入变量 int ledPin 13; int delayPeriod 500;void setup() {pinMode(ledPin, OUTPUT)…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
