二叉树搜索
✅<1>主页:我的代码爱吃辣
📃<2>知识讲解:数据结构——二叉搜索树
☂️<3>开发环境
:Visual Studio 2022
💬<4>前言:在之前的我们已经学过了普通二叉树,了解了基本的二叉树的结构和基本操作了,不过我们之前的二叉树结构都是使用C语言实现的,我们这次来介绍二叉树中更加复杂的树结构,C语言在实现这些结构已经有些吃力了,更适合我们使用C++来实现。
目录
一.前言
二.二叉搜索树
三. 二叉搜索树操作
1.结点与整体结构
2.insert()
3.find()
4.erase()
5.构造与析构
四.二叉搜索树的应用
五. 二叉搜索树的性能分析
六.整体代码
一.前言
map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构,二叉搜索树的特性了解,有助于更好的理解map和set的特性,二叉树中部分面试题稍微有点难度,在前面讲解大家不容易接受,且时间长容易忘。本节借二叉树搜索树,对二叉树部分进行收尾总结。
二.二叉搜索树
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

三. 二叉搜索树操作
1.结点与整体结构
template<class K>
struct BSTreeNode
{BSTreeNode(K key):_key(key),_right(nullptr),_left(nullptr){}K _key; //数值BSTreeNode<K>* _right; //右孩子BSTreeNode<K>* _left; //左孩子
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://...
private:Node* _root = nullptr;
};2.insert()
我们主要针对两种情况:
- 二叉树中一个数据都没有
- 二叉树已经有数据了
如果二叉树中还没有数据,我们需要将插入的第一个数据作为二叉搜索树的根节点。
如果二叉搜索树中,已经有了数据,我们根据搜索二叉树的特性,如果插入的值比根小,我们就往根的左子树去插入,如果插入的值比根大,我们就往根的右子树去插入,如果遇到相同的值就算是插入失败了,循环上面得动作,直到找到一个空位置。

循环版本:
bool insert(const K& key){//如果BSTree还没有结点if (_root == nullptr){_root = new Node(key);return true;}//找到插入的合适位置,和其父亲结点//父亲结点得作用是,我们新插入得结点要和父亲结点连接,//简单来说就是,父亲结点要孩子指针,要指向我们新的结点。Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}//创建新节点cur = new Node(key);//判断新插入得结点是父亲得左孩子还是右孩子if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;}
递归版本:
bool Rinsert(const K& key){return _Rinsert(_root, key);}bool _Rinsert(Node*& root, const K& key){//如果BSTree还没有结点、或者已经找到得合适的空位置if (root == nullptr){root = new Node(key);return true;}//BSTree已经有结点if (key < root->_key){//key比当前结点小,往左树插入return _Rinsert(root->_left, key);}else if (key > root->_key){//key比当前结点大,往右树插入return _Rinsert(root->_right, key);}else{return false;}}//中序遍历void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " " ;_InOrder(root->_right);}测试:
二叉搜索树,中序遍历得结果就是排序结果,我们可以通过这个特性判断我们插入得是否正确。
int main()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> b;BSTree<int> Rb;for (auto e : a){b.insert(e);Rb.Rinsert(e);}b.InOrder();cout << endl;Rb.InOrder();return 0;
}
3.find()
二叉搜索树的查找
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到到空,还没找到,这个值不存在。
找到以后返回目标结点得指针。

循环版本:
Node* find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;}}return nullptr;}递归版本:
Node* Rfind(const K& key){return _Rfind(_root, key);}Node* _Rfind(Node*& root, const K& key){if (root == nullptr){return nullptr;}if (key < root->_key){return _Rfind(root->_left, key);}else if (key > root->_key){return _Rfind(root->_right, key);}else{return root;}}4.erase()
二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否要删除则的结点可能分下面四种情
况:
- a. 要删除的结点无孩子结点
- b. 要删除的结点只有左孩子结点
- c. 要删除的结点只有右孩子结点
- d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程
如下:
- 情况1:要删除的结点只有左孩子结点,删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
- 情况2:要删除的结点只有右孩子结点,删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
- 情况3:要删除的结点有左、右孩子结点,在它的右子树中寻找中序下的第一个结点(数值最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除

情况二与情况一处理方法相同:

循环版本:
bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//准备删除//待删除结点,左节点为空,将其右边结点交给父亲if (cur->_left == nullptr){//此时如果删除的是根节点需要改变根节点指向if (cur == _root){_root = _root->_right;}else{//判断待删除结点是父亲的左孩子还是右孩子if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}//待删除结点,左节点为空,将其左边结点交给父亲else if (cur->_right == nullptr){//此时如果删除的是根节点需要改变根节点指向if (cur == _root){_root = _root->_left;}else{//判断待删除结点是父亲的左孩子还是右孩子if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;return true;} else{//由于删除的结点左右都有孩子//需要找一个能代替删除结点的位置结点,即比左子树大比右子树小//最适合的结点就是,左子树的最右结点(最大节点),右子树的最左节点(最小结点)Node* MinNode = cur->_right;Node* MinParent = cur;while (MinNode->_left){MinParent = MinNode;MinNode = MinNode->_left;}//先将MinNode结点的孩子交给他的父亲//注意:不能因为是找的最左边结点就因为MinNode结点一定是MinParent的左孩子if (MinParent->_left == MinNode){MinParent->_left = MinNode->_right;}else{MinParent->_right = MinNode->_right;}//将MinNode结点的值赋值给curcur->_key = MinNode->_key;delete MinNode;return true;}}}return false;}递归版本:
bool _Rerase(Node*& root, const K& key){//空树、没有找到删除的结点if (root == nullptr){return false;}if (key < root->_key){//key比当前结点小,往左树删除return _Rerase(root->_left, key);}else if(key > root->_key){//key比当前结点小,往左树删除return _Rerase(root->_right, key);}else{//找到,开始删除Node* cur = root;if (root->_left == nullptr){//1.待删除结点,左孩子为空root = root->_right;}else if (root->_right == nullptr){//2.待删除结点,右孩子为空root = root->_left;}else//待删除结点,左右孩子都不为空{//找到左树的最大结点Node* maxleft = root->_left;while (maxleft->_right){maxleft = maxleft->_right;}//交换maxleft和待删除结点的Key值,//并再次转换成左树删除一个单孩子结点,复用上述情况一二的代码swap(maxleft->_key, root->_key);return _Rerase(root->_left, key);}delete cur;}}
测试:
int main()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> b;BSTree<int> Rb;for (auto e : a){b.insert(e);Rb.Rinsert(e);}for (auto e : a){b.erase(e);b.InOrder();cout << endl;Rb.Rerase(e);Rb.InOrder();cout << endl;}return 0;
}
5.构造与析构
拷贝构造:
前序创建结点,后续连接指向。
BSTree(const BSTree<K>& root){_root = _copy(root._root);}Node* _copy(const Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->_key);newnode->_left = _copy(root->_left);newnode->_right = _copy(root->_right);return newnode;}析构函数:
后续销毁结点
~BSTree(){Destroy(_root);}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}默认构造:
如果我们写了拷贝构造,编译器就不会自己生成默认构造函数了,我们可以自己写一个默认构造函数,也可以强制编译器生成一个,但是默认构造只能有一个。
//告诉编译器强制生成BSTree() = default;//自己写BSTree(){}四.二叉搜索树的应用
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到
的值。比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方
式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英
文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出
现次数就是<word, count>就构成一种键值对。
例如:我们将上述的代码改造成K/V结构:
template<class K,class V>
struct BSTreeNode
{BSTreeNode(const K& key, const V& val):_key(key),_val(val),_right(nullptr),_left(nullptr){}K _key;V _val;BSTreeNode<K,V>* _right;BSTreeNode<K,V>* _left;
};template<class K, class V >
class KV_BSTree
{typedef BSTreeNode<K,V> Node;
public:KV_BSTree() = default;KV_BSTree(const KV_BSTree<K,V>& root){_root = _copy(root._root);}~KV_BSTree(){//...}bool insert(const K& key,const V& val){//如果BSTree还没有结点if (_root == nullptr){_root = new Node(key,val);return true;}//找到插入的合适位置,和其父亲结点Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}//判断链接cur = new Node(key,val);if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* find(const K& key){//...}bool erase(const K& key){//...}void InOrder(){_InOrder(_root);}private:void Destroy(Node* root){//...}void _InOrder(Node* root){//...}Node* _root = nullptr;
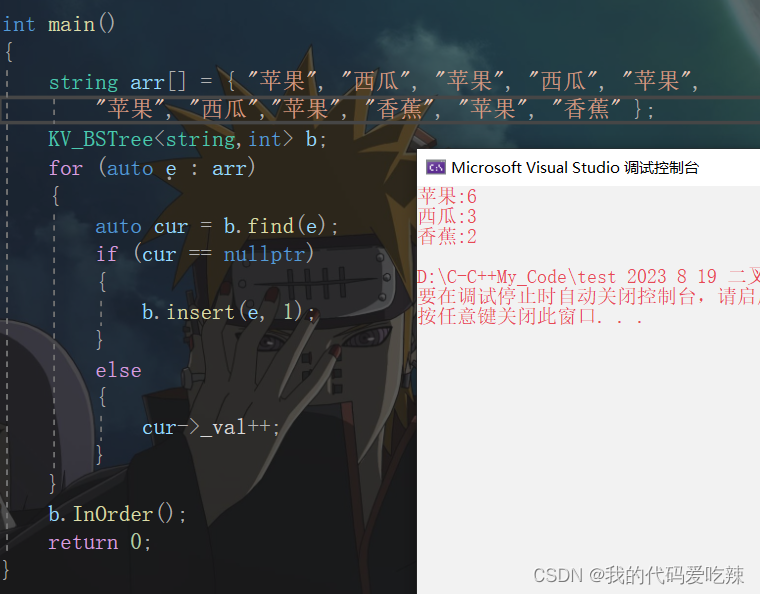
};int main()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };KV_BSTree<string,int> b;for (auto e : arr){auto cur = b.find(e);if (cur == nullptr){b.insert(e, 1);}else{cur->_val++;}}b.InOrder();return 0;
}统计水果出现的次数:
五. 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
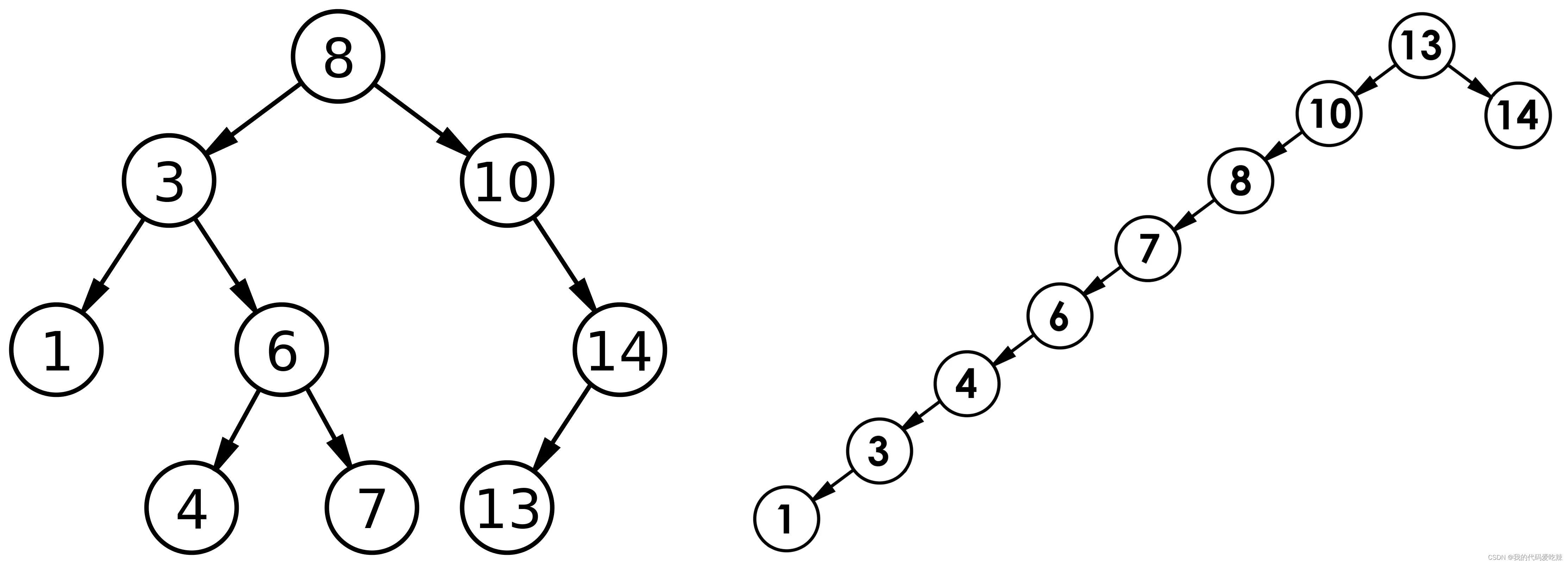
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:$log_2 N$
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:$\frac{N}{2}$
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插
入关键码,二叉搜索树的性能都能达到最优?那么我们后续章节学习的AVL树和红黑树就可以上
场了。
六.整体代码
BSTree.hpp
#pragma once
#include<iostream>
using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode(const K& key):_key(key),_right(nullptr),_left(nullptr){}K _key;BSTreeNode<K>* _right;BSTreeNode<K>* _left;
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://告诉编译器强制生成BSTree() = default;//自己写//BSTree()//{//}BSTree(const BSTree<K>& root){_root = _copy(root._root);}~BSTree(){Destroy(_root);}bool insert(const K& key){//如果BSTree还没有结点if (_root == nullptr){_root = new Node(key);return true;}//找到插入的合适位置,和其父亲结点//父亲结点得作用是,我们新插入得结点要和父亲结点连接,//简单来说就是,父亲结点要孩子指针,要指向我们新的结点。Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}//创建新节点cur = new Node(key);//判断新插入得结点是父亲得左孩子还是右孩子if (key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;}}return nullptr;}bool erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//准备删除//待删除结点,左节点为空,将其右边结点交给父亲if (cur->_left == nullptr){//此时如果删除的是根节点需要改变根节点指向if (cur == _root){_root = _root->_right;}else{//判断待删除结点是父亲的左孩子还是右孩子if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}//待删除结点,左节点为空,将其左边结点交给父亲else if (cur->_right == nullptr){//此时如果删除的是根节点需要改变根节点指向if (cur == _root){_root = _root->_left;}else{//判断待删除结点是父亲的左孩子还是右孩子if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;return true;} else{//由于删除的结点左右都有孩子//需要找一个能代替删除结点的位置结点,即比左子树大比右子树小//最适合的结点就是,左子树的最右结点(最大节点),右子树的最左节点(最小结点)Node* MinNode = cur->_right;Node* MinParent = cur;while (MinNode->_left){MinParent = MinNode;MinNode = MinNode->_left;}//先将MinNode结点的孩子交给他的父亲//注意:不能因为是找的最左边结点就因为MinNode结点一定是MinParent的左孩子if (MinParent->_left == MinNode){MinParent->_left = MinNode->_right;}else{MinParent->_right = MinNode->_right;}//将MinNode结点的值赋值给curcur->_key = MinNode->_key;delete MinNode;return true;}}}return false;}bool Rerase(const K& key){return _Rerase(_root,key);}Node* Rfind(const K& key){return _Rfind(_root, key);}bool Rinsert(const K& key){return _Rinsert(_root, key);}void InOrder(){_InOrder(_root);}private:Node* _copy(const Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->_key);newnode->_left = _copy(root->_left);newnode->_right = _copy(root->_right);return newnode;}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}bool _Rerase(Node*& root, const K& key){//空树、没有找到删除的结点if (root == nullptr){return false;}if (key < root->_key){//key比当前结点小,往左树删除return _Rerase(root->_left, key);}else if(key > root->_key){//key比当前结点小,往左树删除return _Rerase(root->_right, key);}else{//找到,开始删除Node* cur = root;if (root->_left == nullptr){//1.待删除结点,左孩子为空root = root->_right;}else if (root->_right == nullptr){//2.待删除结点,右孩子为空root = root->_left;}else//待删除结点,左右孩子都不为空{//找到左树的最大结点Node* maxleft = root->_left;while (maxleft->_right){maxleft = maxleft->_right;}//交换maxleft和待删除结点的Key值,//并再次转换成左树删除一个单孩子结点,复用上述情况一二的代码swap(maxleft->_key, root->_key);return _Rerase(root->_left, key);}delete cur;}}Node* _Rfind(Node*& root, const K& key){if (root == nullptr){return nullptr;}if (key < root->_key){return _Rfind(root->_left, key);}else if (key > root->_key){return _Rfind(root->_right, key);}else{return root;}}bool _Rinsert(Node*& root, const K& key){//如果BSTree还没有结点if (root == nullptr){root = new Node(key);return true;}//BSTree已经有结点if (key < root->_key){//key比当前结点小,往左树插入return _Rinsert(root->_left, key);}else if (key > root->_key){//key比当前结点大,往右树插入return _Rinsert(root->_right, key);}else{return false;}}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " " ;_InOrder(root->_right);}Node* _root = nullptr;
};
相关文章:

二叉树搜索
✅<1>主页:我的代码爱吃辣📃<2>知识讲解:数据结构——二叉搜索树☂️<3>开发环境 :Visual Studio 2022💬<4>前言:在之前的我们已经学过了普通二叉树,了解了基本的二叉树…...
【先进PID控制算法(ADRC,TD,ESO)加入永磁同步电机发电控制仿真模型研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
k8s集群生产环境的问题处理
2 k8s上的服务均无法访问 执行命令kubectl get pods -ALL,k8s集群中的服务均是running状态 1 kuboard 网页无法访问 kuboard无法通过浏览器访问,但是查看端口是被占用的...
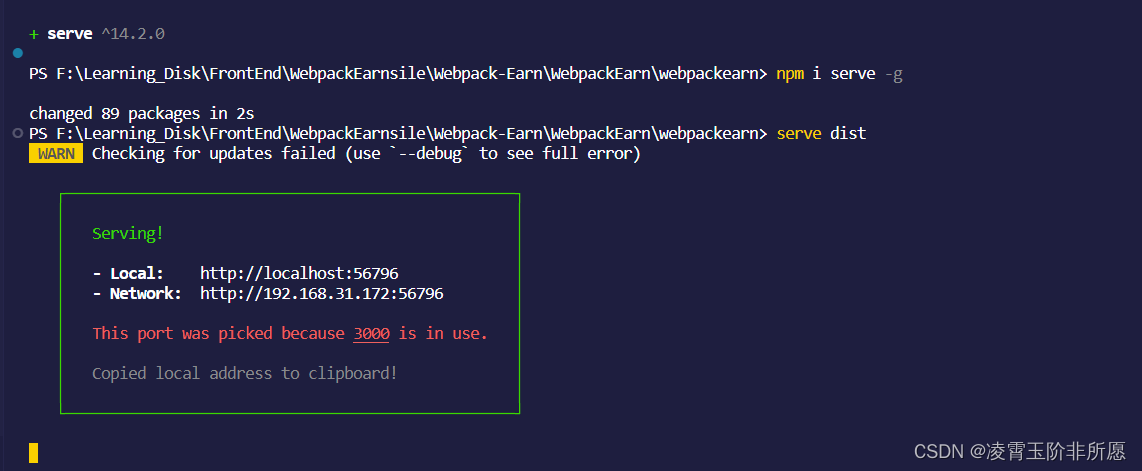
serve : 无法将“serve”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。
1、在学习webpack打包的时候,需要 serve用来启动开发服务器来部署代码查看效果的。安装完之后运行出现以下错误: 2、使用命令查看安装目录: npm list -g我们已经安装过了 3、解决: 我们看到上图路径在:C:\Users\qiy…...
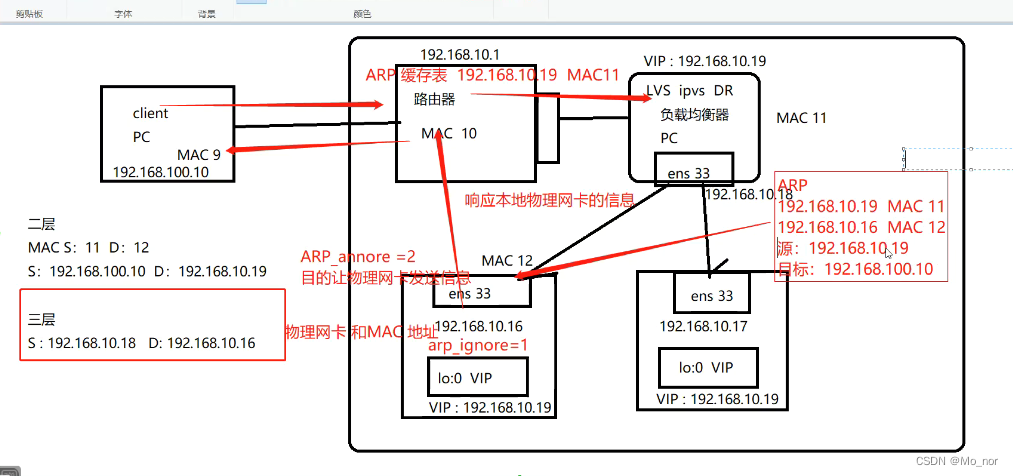
【LVS】2、部署LVS-DR群集
LVS-DR数据包的流向分析 1.客户端发送请求到负载均衡器,请求的数据报文到达内核空间; 2.负载均衡服务器和正式服务器在同一个网络中,数据通过二层数据链路层来传输; 3.内核空间判断数据包的目标IP是本机VIP,此时IP虚…...
)
设计模式 -- 单例模式(传统面向对象与JavaScript 的对比实现)
单例模式 – 传统面向对象与JavaScript 的对比实现 文章目录 单例模式 -- 传统面向对象与JavaScript 的对比实现传统的面向对象的实现定义实现思路初级实现缺点 透明的单例模式实现目的(实现效果)实现缺点 用代理实现单例模式优点 JavaScript 中的单例模…...
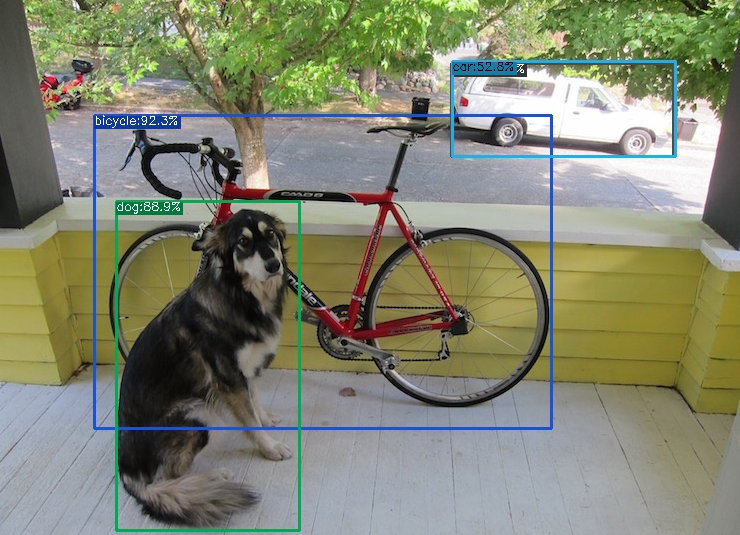
YOLOX算法调试记录
YOLOX是在YOLOv3基础上改进而来,具有与YOLOv5相媲美的性能,其模型结构如下: 由于博主只是要用YOLOX做对比试验,因此并不需要对模型的结构太过了解。 先前博主调试过YOLOv5,YOLOv7,YOLOv8,相比而言,YOLOX的环…...
基于小程序的汽车俱乐部系统的设计与实现(论文+源码)_kaic
目录 前 言 1 系统概述 1.1 系统主要功能 1.2 开发及运行环境 2 系统分析和总体设计 2.1 需求分析 2.2 可行性分析 2.3 设计目标 2.4 项目规划 2.5 系统开发语言简介 2.6 系统功能模块图 3 系统数据库设计 3.1 数据库开发工具简介 3.2 数据库需求分析 3.3 数据库…...

ProgrammingArduino物联网
programming_arduino_ed2 IO 延时闪灯 void setup() {pinMode(13, OUTPUT); }void loop() {digitalWrite(13, HIGH);delay(500);digitalWrite(13, LOW);delay(500); }// sketch 03-02 加入变量 int ledPin 13; int delayPeriod 500;void setup() {pinMode(ledPin, OUTPUT)…...

SSM框架的学习与应用(Spring + Spring MVC + MyBatis)-Java EE企业级应用开发学习记录(第一天)Mybatis的学习
SSM框架的学习与应用(Spring Spring MVC MyBatis)-Java EE企业级应用开发学习记录(第一天)Mybatis的学习 一、当前的主流框架介绍(这就是后期我会发出来的框架学习) Spring框架 Spring是一个开源框架,是为了解决企业应用程序开发复杂…...

Programming abstractions in C阅读笔记: p118-p122
《Programming Abstractions In C》学习第49天,p118-p122,总结如下: 一、技术总结 1.随机数 (1)seed p119,“The initial value–the value that is used to get the entire process start–is call a seed for the random ge…...

2023国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
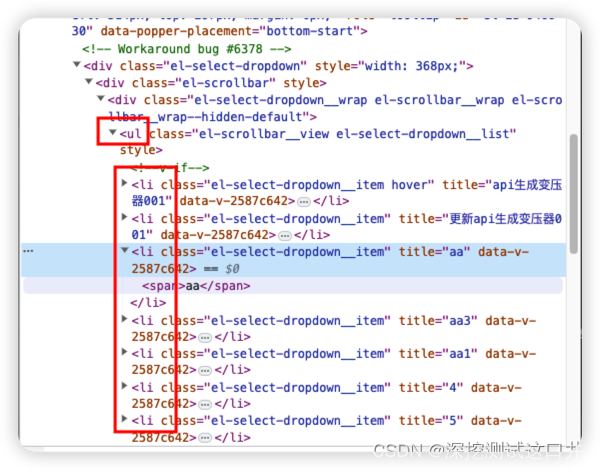
selenium 选定ul-li下拉选项中某个指定选项
场景:selenium的下拉选项是ul-li模式,选定某个指定的选项。 from selenium.webdriver.support.ui import WebDriverWait from selenium.webdriver.support import expected_conditions as EC # 显示等待def select_li(self, text, *ul_locator):"…...

回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)效果一览基本介绍…...

使用pytorch 的Transformer进行中英文翻译训练
下面是一个使用torch.nn.Transformer进行序列到序列(Sequence-to-Sequence)的机器翻译任务的示例代码,包括数据加载、模型搭建和训练过程。 import torch import torch.nn as nn from torch.nn import Transformer from torch.utils.data im…...

解决element的select组件创建新的选项可多选且opitions数据源中有数据的情况下,回车不能自动选中创建的问题
前言 最近开发项目使用element-plus库内的select组件,其中有提供一个创建新的选项的用法,但是发现一些小问题,在此记录 版本 “element-plus”: “^2.3.9”, “vue”: “^3.3.4”, 问题 1、在options数据源中无数据的时候,在输入框…...
人工智能大模型加速数据库存储模型发展 行列混合存储下的破局
数据存储模型 专栏内容: postgresql内核源码分析手写数据库toadb并发编程toadb开源库 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 概述 在数据库的发展过程中,关…...
K8S用户管理体系介绍
1 K8S账户体系介绍 在k8s中,有两类用户,service account和user,我们可以通过创建role或clusterrole,再将账户和role或clusterrole进行绑定来给账号赋予权限,实现权限控制,两类账户的作用如下。 server acc…...
实现chatGPT 聊天样式
效果图 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Chat Example</title&g…...

day9 STM32 I2C总线通信
I2C总线简介 I2C总线介绍 I2C(Inter-Integrated Circuit)总线(也称IIC或I2C)是由PHILIPS公司开发的两线式串行总线,用于连接微控制器及其外围设备,是微电子通信控制领域广泛采用的一种总线标准。 它是同步通…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
