卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network
卷积计算公式:N = (W-F+2p)/s+1
这个公式每次都得看看,不能忘
1 经典网络
按照时间顺序
1.1 LeNet
LeNet是 Yann LeCun在1998年提出,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。
深度学习开山之作LeNet实战:(现代卷积神经网络/网络结构/原理解析/源码解读)、《Gradient-Based Learning Appliedto Document Recognition》_会害羞的杨卓越的博客-CSDN博客
1.2 AlexNet
深度学习奠基作AlexNet《ImageNet Classification with Deep Convolutional Neural Networks》之论文解读上篇_会害羞的杨卓越的博客-CSDN博客
AlexNet网络结构详解_会害羞的杨卓越的博客-CSDN博客
AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的,把CNN的基本原理应用到了很深很宽的网络中。
主要参数:AlexNet网络包含8层,其中前5层为卷积-池化层,后3层为全连接层;输入224×224×3的图像,第一卷积层用96个11×11×3的卷积核对进行滤波,步幅4像素;全连接的每层有4096个神经元,最后一个完全连接的层的输出被馈送到1000路SoftMax,它产生超过1000个类别标签的分布;整个网络共650000个神经元。
特点:
- 使用ReLU作为激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题
- 使用Dropout(丢弃学习)随机忽略一部分神经元防止过拟合
- 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果
- 提出了LRN(Local Response Normalization,局部正规化)层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力
- 使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算
1.3 VGG
- 网络深度:16-19层
- 5组卷积-池化,3个全连接
- 三个全连接层,前两层都有4096通道,第三层共1000路及代表1000个标签类别;最后一层为softmax层
- 所有卷积层有相同的配置,即卷积核大小为3x3,步长为1,填充为1
深度学习奠基作VGG《Very Deep Convolutional Networks for Large-Scale Image Recognition》(现代卷积神经网络/网络结构)_会害羞的杨卓越的博客-CSDN博客
1.4 GoogleNet
深度学习奠基作GoogleNet《Very Deep Convolutional Networks for Large-Scale Image Recognition》(现代卷积神经网络/网络结构)_会害羞的杨卓越的博客-CSDN博客
1.5 ResNet
深度学习最强奠基作ResNet《Deep Residual Learning for Image Recognition》论文解读(上篇)_会害羞的杨卓越的博客-CSDN博客
2 网络结构
2.1 卷积层
通过卷积操作,进行特征提取和降维。
2.2 激活层
将前一层的输出,通过非线性的激活函数进行处理,用以模拟任意维度的函数,增强网络的表征能力。
常用的激活函数:
- 阶跃函数(用的较少)
- sigmoid函数:
- 优点:平滑,易求导
- 缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练
- 改善方案:归一化,用sk-learn函数处理
- tanh函数 常用于NLP,其他类似sigmiod函数
- Relu函数(常用),优点:
- 更加有效率的梯度下降以及反向传播,避免了梯度爆炸和梯度消失问题
- 计算过程简单
- softmax函数,特点:多分类模型适用
2.3 池化
也称子采样层或下采样层(Subsampling Layer),目的是缩小高、长方向上的空间的运算,以降低计算量,提高泛化能力。
计算方式:
- Max池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域取最大值,形成的新矩阵。在图像识别领域,主要使用Max池化
- Average池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域计算平均值
池化层特征:
- 没有要学习的参数。池化层和卷积层不同,没有要学习的参数。池化只是从目标区域中取最大值(或者平均值),所以不存在要学习的参数
- 通道数不发生变化。经过池化运算,输入数据和输出数据的通道数不会发生变化
- 对微小的位置变化具有鲁棒性(健壮)。输入数据发生微小偏差时,池化仍会返回相同的结果
2.4 全连接层
这个网络层相当于多层感知机(Multi-Layer Perceptron,简称MLP),其在整个卷积神经网络中起到分类器的作用。
通过前面多个“卷积-激活-池化”层的反复处理,待处理的数据特性已有了显著提高:一方面,输入数据的维度已下降到可用传统的前馈全连接网络来处理了;另一方面,此时的全连接层输入的数据已不是“泥沙俱下、鱼龙混杂”,而是经过反复提纯过的结果,因此输出的分类品质要高得多。
相关文章:

卷积神经网络全解:(AlexNet/VGG/ GoogLeNet/LeNet/ResNet/卷积/激活/池化/全连接)、现代卷积神经网络、经典卷积神经网络
CNN,卷积神经网络,Convolution Neural Network 卷积计算公式:N (W-F2p)/s1 这个公式每次都得看看,不能忘 1 经典网络 按照时间顺序 1.1 LeNet LeNet是 Yann LeCun在1998年提出,用于解决手…...
简述)
WDM 模型(Windows Driver Model)简述
WDM 模型(Windows Driver Model) 是微软公司为 Windows98 和 Windows2000 的驱动程序设计的一种架构,在 WDM 驱动程序模型中,每个硬件设备 至少有两个驱动程序。其中一个为功能驱动程序,它了解硬件工作的所有细节,负 责初始化 …...

【算法刷题之数组篇(1)】
目录 1.leetcode-59. 螺旋矩阵 II(题2.题3相当于二分变形)2.leetcode-33. 搜索旋转排序数组3.leetcode-81. 搜索旋转排序数组 II(与题目2对比理解)(题4和题5都是排序双指针)4.leetcode-15. 三数之和5.leetcode-18. 四数之和6.leet…...

【数据挖掘】使用 Python 分析公共数据【01/10】
一、说明 本文讨论了如何使用 Python 使用 Pandas 库分析官方 COVID-19 病例数据。您将看到如何从实际数据集中收集见解,发现乍一看可能不那么明显的信息。特别是,本文中提供的示例说明了如何获取有关疾病在不同国家/地区传播速度的信息。 二、准备您的…...

html怎么插入视频?视频如何插入页面
html怎么插入视频?视频如何插入页面 HTML 的功能强大,基本所有的静态效果都可以在此轻松呈现,各种视频网站内有大量的视频内容,本篇文章教你如何在 html 中插入视频 代码如下: <!DOCTYPE html> <html> …...
游戏服务端性能测试
导语:近期经历了一系列的性能测试,涵盖了Web服务器和游戏服务器的领域。在这篇文章中,我将会对游戏服务端所做的测试进行详细整理和记录。需要注意的是,本文着重于记录,而并非深入的编程讨论。在这里,我将与…...
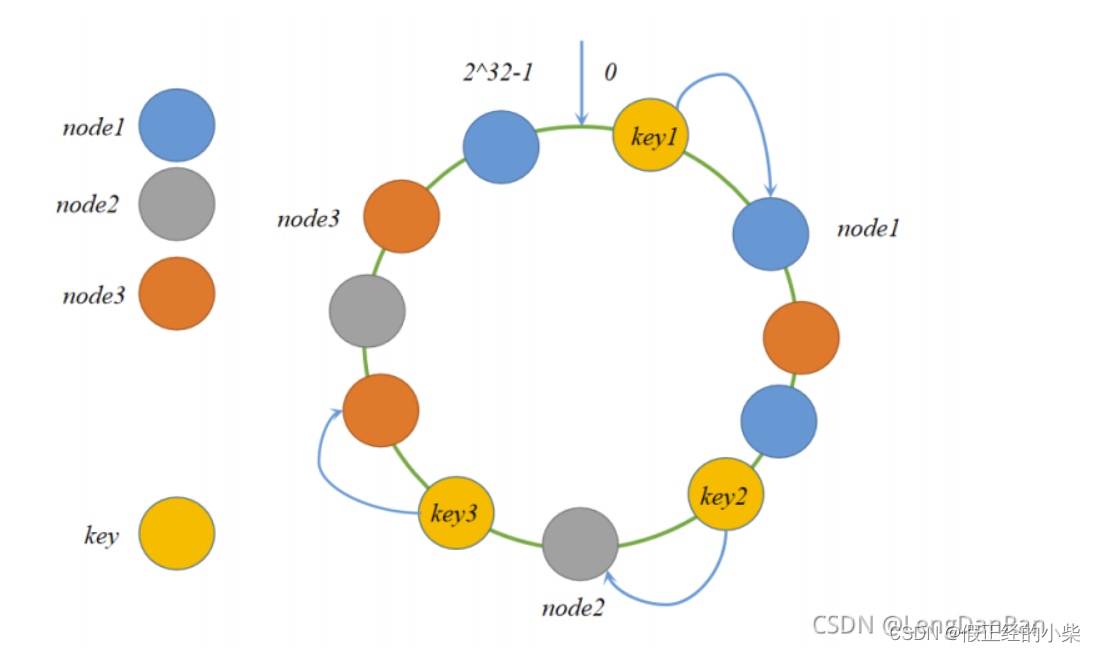
【使用Zookeeper当作注册中心】自己定制负载均衡常见策略
自己定制负载均衡常见策略 一、前言随机(Random)策略的实现轮询(Round Robin)策略的实现哈希(Hash)策略 一、前言 大伙肯定知道,在分布式开发中,目前使用较多的注册中心有以下几个&…...
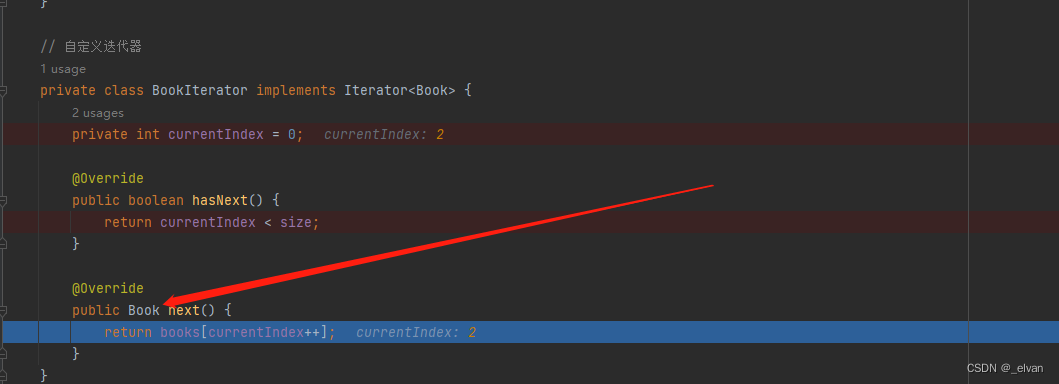
设计模式十七:迭代器模式(Iterator Pattern)
迭代器模式(Iterator Pattern)是一种行为型设计模式,它提供了一种访问聚合对象(例如列表、集合、数组等)中各个元素的方法,而无需暴露其内部表示。迭代器模式将遍历元素和访问元素的责任分离开来࿰…...

Python制作爱心并打包成手机端可执行文件
前言 本文是想要将python代码打包成在手机上能执行的文件 尝试了几个库, 有这也那样的限制,最终还是选了BeeWare 环境:python3.7.x 开始 找到打包有相关工具os-android-apk-builder,buildozer,cx_Freezeÿ…...
以及多容器通信和统一配置)
使用docker-compose.yml快速搭建开发、部署环境(nginx、tomcat、mysql、jar包、各种程序)以及多容器通信和统一配置
目录 docker-compose语法(更多说明可查看下面代码)imagehostnamecontainer_namevolumesnetworks yml文件的使用启动停止 开发环境(这里以python为例)部署环境nginxmysqltomcatjar包打包后的可执行程序 常见问题与解决方案多个容器…...

管理类联考——逻辑——真题篇——按知识分类——汇总篇——二、论证逻辑——支持加强——第三节——分类3——类比题干支持
文章目录 第三节 支持加强-分类3-类比题干支持真题(2017-28)-支持加强-正面支持-表达“确实如此”真题(2017-36)-支持加强-正面支持-表达“确实如此”真题(2017-39)-支持加强-正面支持-方法有效或方法可行,但多半不选择方法无恶果真题(2017-50)-支持加强真题(2018-2…...

搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nums[1], …, …...

Steam搬砖项目:最长久稳定的副业!
项目应该大家都有听说话,但是细节问题,如何操作可能有些不是很清楚,今天在这里简单分享一下。 这个Steam搬砖项目主要赚钱汇率差和价值差,是一个细分领取的小项目。 不用引流,时间也是比较自由的,你可以兼…...
最小化安装移动云大云操作系统--BCLinux-R8-U8-Server-x86_64-230802版
CentOS 结束技术支持,转为RHEL的前置stream版本后,国内开源Linux服务器OS生态转向了开源龙蜥和开源欧拉两大开源社区,对应衍生出了一系列商用Linux服务器系统。BC-Linux V8.8是中国移动基于龙蜥社区Anolis OS 8.8版本深度定制的企业级X86服务…...

神经网络基础-神经网络补充概念-05-导数
概念 导数是微积分中的一个概念,用于描述函数在某一点的变化率。在数学中,函数的导数表示函数值随着自变量的微小变化而产生的变化量,即斜率或变化率。 假设有一个函数 f(x),其中 x 是自变量,y f(x) 是因变量。函数…...

kubernetes — 安装Ingress
1、 Ingress 1、安装-Nginx-Ingress kubectl apply -f https://raw.githubusercontent.com/kubernetes/ingress-nginx/controller-v1.8.1/deploy/static/provider/cloud/deploy.yaml 2、设为默认的Ingress [rootk8s01 ~]# vim default_ingress.yaml apiVersion: networking.…...

SSR使用HTTPS
1.安装 npm i browser-sync 2. 再angular.json里配置 "serve-ssr": {"builder": "nguniversal/builders:ssr-dev-server","options": {"ssl": true,"sslCert": "./node_modules/browser-sync/certs/server…...

Spring Boot中使用validator如何实现接口入参自动检验
文章目录 一、背景二、使用三、举例 一、背景 在项目开发过程中,经常会对一些字段进行校验,比如字段的非空校验、字段的长度校验等,如果在每个需要的地方写一堆if else 会让你的代码变的冗余笨重且相对不好维护,如何更加规范和优…...

thinkphp 5 实现UNION ALL 3个联表查询,并且带上搜索条件,名称,时间,手机号
在ThinkPHP 5中实现带有搜索条件、名称、时间和手机号的3个联表查询(UNION ALL),您可以按照以下步骤进行操作: 确保已经配置好数据库连接信息和相关的模型。 使用union()方法来构建3个联表查询,同时在每个查询中添加所…...
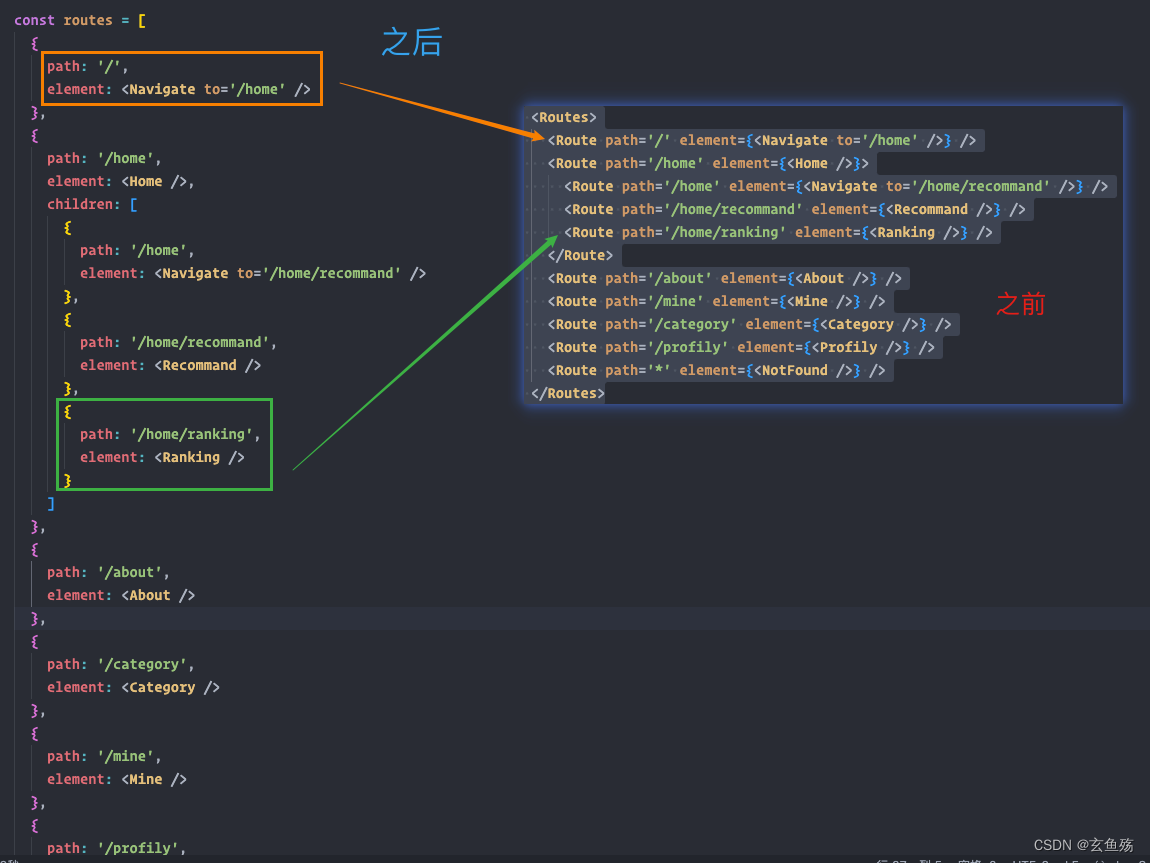
React 之 Router - 路由详解
一、Router的基本使用 1. 安装react-router react-router会包含一些react-native的内容,web开发并不需要 npm install react-router-dom 2. 设置使用模式 BrowserRouter或HashRouter Router中包含了对路径改变的监听,并且会将相应的路径传递给子组件Bro…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
