LeetCode——51. N 皇后
一、题目
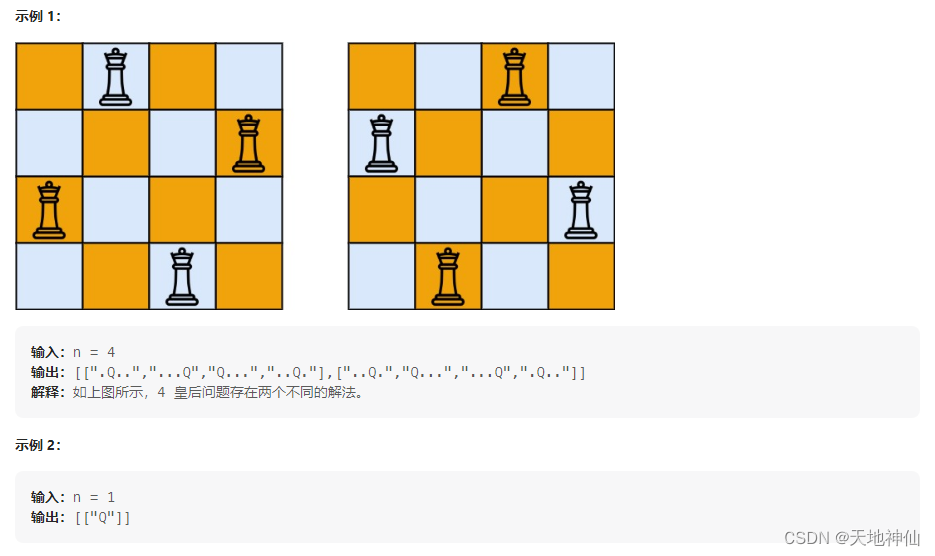
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/n-queens/description/
二、C++解法
我的思路及代码
采用回溯的思想。这里需要一个判断的函数 isValid ,来处理当前位置是否是可选的位置。每一次选择的时候都会前进一行,然后在当前行中,选择可用的列。如果这个列是可用的那么就可以选择此路径,然后继续后面的回溯,如果不可用则继续往下找。本质是一个全排列的问题。由于我们的方式是从一行一行的往下找,那么在 isValid 中,就不必判定左下角和右下角的合理情况,这必然是可选的。
class Solution {
public:vector<vector<string>> ans;bool isValid(int &row,int &col,vector<string> &temp){int rowTemp = row;int colTemp = col;//判断列有没有棋子for(int i=0;i<temp.size();i++){if(temp[i][col] == 'Q')return false;}//判断左上有没有棋子for(;rowTemp>=0&&colTemp>=0;rowTemp--,colTemp--){if(temp[rowTemp][colTemp] == 'Q')return false;}//判断右上有没有棋子for(rowTemp = row,colTemp = col;rowTemp>=0&&colTemp<temp.size();rowTemp--,colTemp++){if(temp[rowTemp][colTemp] == 'Q')return false;}return true;}void backtrance(vector<string> &temp,int row){if(row==temp.size()){ans.push_back(temp);return;}for(int col=0;col<temp.size();col++){if(isValid(row,col,temp)){temp[row][col] = 'Q';backtrance(temp,row+1);temp[row][col] = '.';}}}vector<vector<string>> solveNQueens(int n) {vector<string> temp(n,string(n,'.'));backtrance(temp,0);return ans;}
};
- 时间复杂度:O(N!),其中 N 是皇后数量
- 空间复杂度:O(N),其中 N 是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N
官方参考代码
方法一:基于集合的回溯
采用了集合的方式来存储各个线上皇后的情况,本质还是回溯算法。
class Solution {
public:vector<vector<string>> solveNQueens(int n) {auto solutions = vector<vector<string>>();auto queens = vector<int>(n, -1);auto columns = unordered_set<int>();auto diagonals1 = unordered_set<int>();auto diagonals2 = unordered_set<int>();backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);return solutions;}void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {if (row == n) {vector<string> board = generateBoard(queens, n);solutions.push_back(board);} else {for (int i = 0; i < n; i++) {if (columns.find(i) != columns.end()) {continue;}int diagonal1 = row - i;if (diagonals1.find(diagonal1) != diagonals1.end()) {continue;}int diagonal2 = row + i;if (diagonals2.find(diagonal2) != diagonals2.end()) {continue;}queens[row] = i;columns.insert(i);diagonals1.insert(diagonal1);diagonals2.insert(diagonal2);backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);queens[row] = -1;columns.erase(i);diagonals1.erase(diagonal1);diagonals2.erase(diagonal2);}}}vector<string> generateBoard(vector<int> &queens, int n) {auto board = vector<string>();for (int i = 0; i < n; i++) {string row = string(n, '.');row[queens[i]] = 'Q';board.push_back(row);}return board;}
};
- 时间复杂度:O(N!),其中 N 是皇后数量
- 空间复杂度:O(N),其中 N 是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N
相关文章:

LeetCode——51. N 皇后
一、题目 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案…...

jQuery基本操作
学习目标: 会使用基本选择器获取元素 会使用层次选择器获取元素 会使用属性选择器获取元素 会使用过滤选择器获取元素 学习内容: 1.回顾jQuery语法结构 语法 $(selector).action; 工厂函数$():将DOM对象转化为jQuery对象。 选择器 sele…...
基于蜣螂算法优化Kmeans图像分割-附代码
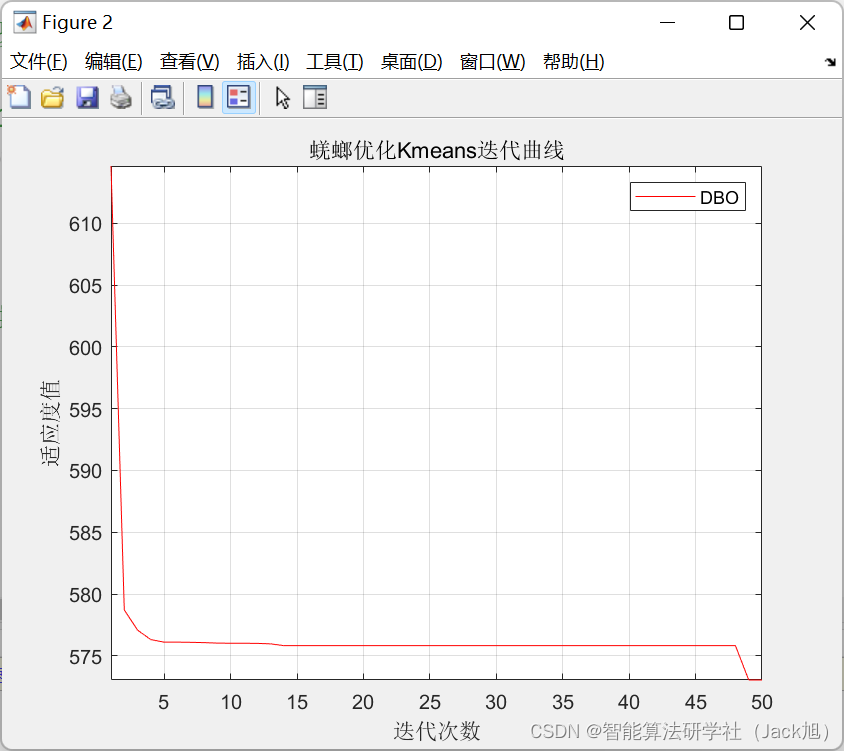
基于蜣螂优化Kmeans图像分割算法 - 附代码 文章目录基于蜣螂优化Kmeans图像分割算法 - 附代码1.Kmeans原理2.基于蜣螂算法的Kmeans聚类3.算法实验结果4.Matlab代码摘要:基于蜣螂优化Kmeans图像分割算法。1.Kmeans原理 K-Means算法是一种无监督分类算法,…...
第二章 Kafka设计原理详解
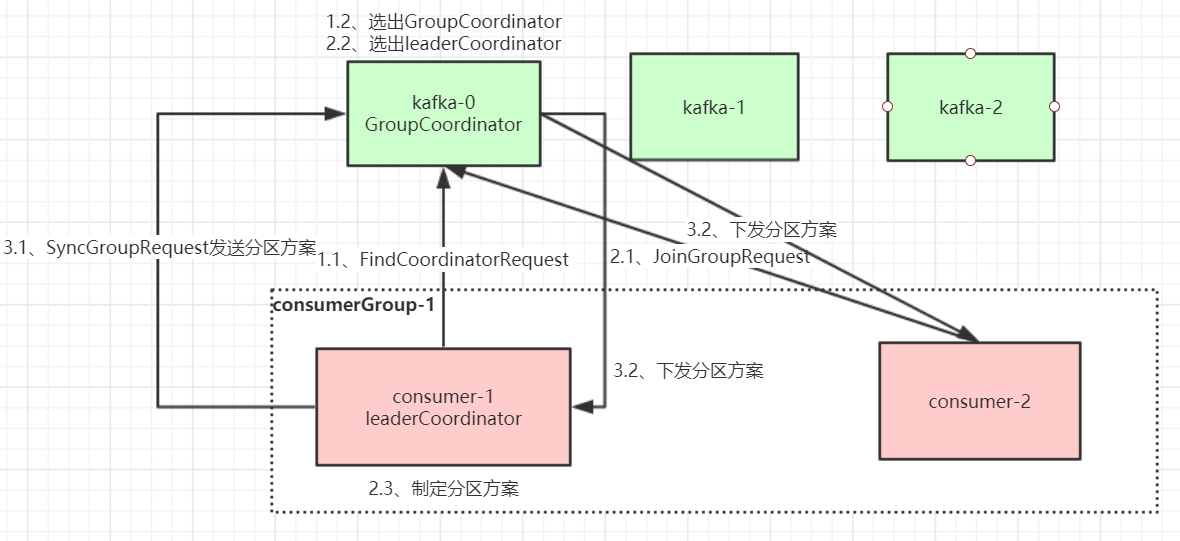
第二章 Kafka设计原理详解 1、Kafka核心总控制器Controller 在 Kafka 集群中会有一个或者多个 broker,其中有一个 broker 会被选举为控制器(Kafka Controller),它负责管理整个集群中所有分区和副本的状态。 当某个分区的 leader…...

《NFL橄榄球》:费城老鹰·橄榄1号位
费城老鹰(英语:Philadelphia Eagles)是美国橄榄球联盟在宾夕法尼亚州费城的一支球队。1933年在国家橄榄球联盟扩编时与匹兹堡钢人和辛辛那提红人一起加入;1943年赛季因二次大战的缘故,和匹兹堡钢人作短暂的合并。 在20…...
【人工智能AI】四、NoSQL进阶《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章的标题是《四、NoSQL进阶》,不少于3000字。帮我细化到三级目录,使用markdown格式。这篇文章的目录是: 四、NoSQL 进阶 4.1 NoSQL 高可用 4.2 NoSQL 数据安全 4.3 NoSQL 性能优化 4.4 总结 四、…...
K8S 部署 Jenkins
本文使用 bitnami 镜像部署 Jenkins 官方文档:https://github.com/bitnami/charts/tree/main/bitnami/jenkins 添加 bitnami 仓库 helm repo add bitnami https://charts.bitnami.com/bitnami自定义 values.yaml storageClass:集群的存储类ÿ…...

【人工智能AI】五、NoSQL 应用实践《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章的标题是《五、NoSQL 应用实践》,不少于3000字。目录需要细化到三级目录,使用markdown格式。这篇文章的大的目录是: 五、NoSQL 应用实践 5.1 NoSQL 实时数据分析 5.2 NoSQL 分布式系统 5.3 NoS…...
Java爬虫系列 - 爬虫补充内容+ElasticSearch展示数据
一,定时任务Cron表达式Component public class TaskTest {Scheduled(cron "0/5 * * * * *") // 从0秒开始,每个五秒 执行一次 { 秒 分 时 天 月 周 }public void test(){System.out.println("定时任务执行了");} }二,网…...

Typora常用快捷键
Typora常用快捷键大全 ctrl1到6:1~6级标题,标题用ctrlH是没用的 ctrlshiftk:随时随地插入代码块,极为方便。 ctrlt:创建表格,也可直接输入|列1|列2|列3|并回车来创建表 ctrlshiftq:能实现添加…...
开学季好用电容笔有哪些?好用实惠的电容笔推荐
随着科学技术的快速发展,ipad的影响力越来越大,而且ipad的用户也越来越多,如果要提高ipad的功能,让ipad更加有趣,那么就需要一款非常适合自己,并且非常实用的电容笔。那么,究竟该选择哪个品牌的…...
C++_复习Recording
文章目录C复习课填空题编程题C复习课 试卷说明: 题型: 填空 编程题目 填空题 构造函数无返回类型,与类名同名; 复制构造函数用于创建对象,形实参结合,返回和接收对象。 补充: 只有在声明语句中使用一个变…...
【java】Spring Cloud --Spring Cloud 的核心组件
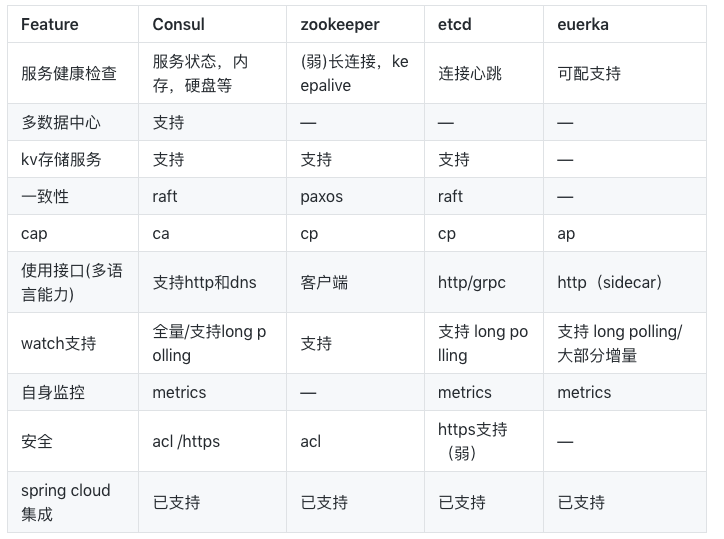
文章目录前言一、Eureka(注册中心)二、Zuul(服务网关)三、 Ribbon(负载均衡)四、Hystrix(熔断保护器)五、 Feign(REST转换器)六、 Config(分布式配…...
【C++】RBTree——红黑树
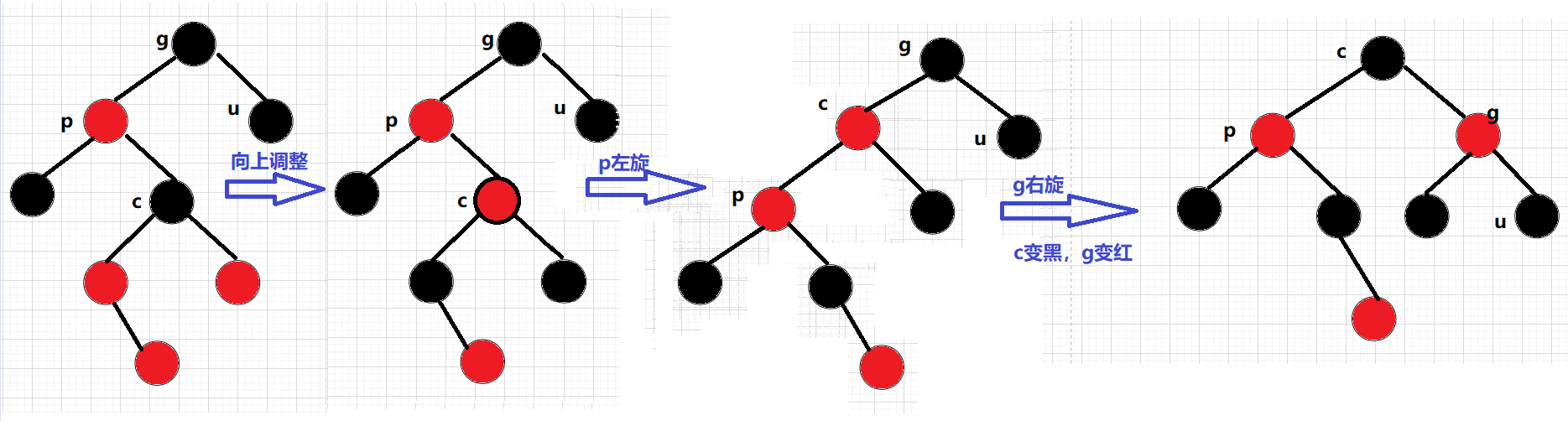
文章目录一、红黑树的概念二、红黑树的性质三、红黑树节点的定义四、红黑树的插入五、代码实现一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上…...

【5G RRC】5G系统消息SIB2介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

自托管提醒平台Noted Reminders
什么是 Noted Reminders ? Noted 是一个简单的自托管应用程序,用于创建使用 Apprise API 推送到设备的提醒。您可以向几乎每个平台发送消息,包括定时电子邮件! 什么是 Apprise API ? Apprise 允许您向我们今天可用的几乎所有最流…...

LockSupport常用方法源码分析
前言:本文将介绍LockSupport类中的方法和部分源码,以及面试常问到的一个小问题,感兴趣的大佬可以指点下。 希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么需要改进的地方还请大佬不吝赐教&am…...

Mybatis Notes
文章目录1 Mybatis 介绍1.1 快速入门2 JDBC2.1 JDBC介绍2.3 JDBC问题分析2.4 Mybatis与JDBC技术对比3 数据库连接池3.1 数据库连接池介绍3.2 数据库连接池产品产品3.3 Druid引入项目4lombok4.1 lombok介绍4.2 lombok使用4.2.1 在pom.xml文件中引入依赖4.2.2 pojo类代码引入1 My…...
MySQL 10:MySQL事务
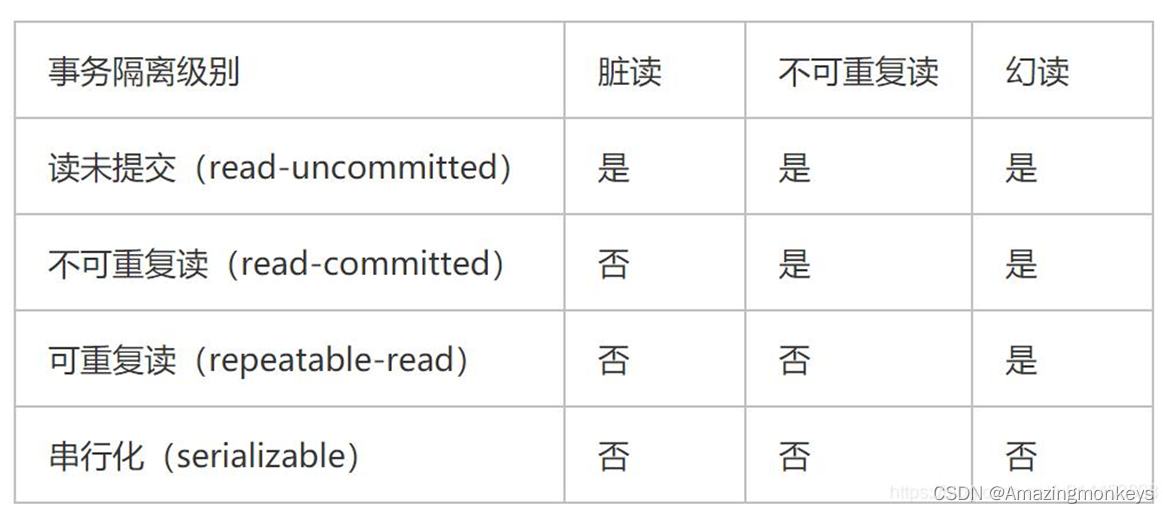
MySQL 中的事务是由存储引擎实现的。在 MySQL 中,只有 InnoDB 存储引擎支持事务。事务处理可用于维护数据库的完整性,确保批处理的 SQL 语句要么执行要么根本不执行。事务用于管理 DDL、DML 和 DCL 操作,例如插入、更新和删除语句,…...
软件设计(十三)-原码、反码、补码、移码
软件设计(十二)数据结构(下)https://blog.csdn.net/ke1ying/article/details/129035300 下面把一个数转成二进制表达形式 原码: 数值1 : 0000 0001 数值-1 : 1000 0001 1 (- 1) : 1000 0010 这是8个…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
