C++set集合与并查集map映射,哈希表应用实例B3632 集合运算 1P1918 保龄球
集合的性质
- 无序性
- 互异性
- 确定性
B3632 集合运算 1
题面
题目背景
集合是数学中的一个概念,用通俗的话来讲就是:一大堆数在一起就构成了集合。
集合有如下的特性:
-
无序性:任一个集合中,每个元素的地位都是相同的,元素之间是无序的。
-
互异性:一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。
-
确定性:给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
元素 a 属于集合 A 记作 a∈A,反之则记作 a∈/A。
若一个集合中不存在任何元素,则称该集合为空集,记作 ∅。空集是所有集合的子集。
一个集合内的元素个数称为该集合的大小。A 集合的大小可记作 ∣A∣。
集合 C 是集合 A 与 B 的交集,当且仅当对于任何元素 a∈C,有 a∈A 且 a∈B,并且对于任何元素 b∈/C,有 b∈/A 或 b∈/B。记作 A∩B。
简单地说,交集是由所有同时属于两个集合的元素所构成的,就像两个集合相交;而并集是由所有属于其中任意一个集合的元素所构成的,就像两个集合合并。
特别地,对于形如 {x∣a≤x≤b} 的集合,可以记作 [a,b]。其中,如果左侧符号改为小于号,则左侧中括号改为小括号。右侧同理。
题目描述
现在给予两个集合 A 和 B,均由 00 到 6363 之间的整数组成。
请依次求出:
- ∣A∣
- A∩B
- A∪B
输入格式
输入四行。
第一行一个整数 x(0≤x≤63),表示集合 A 的元素个数。
第二行 x 个整数 a1,...ax,表示集合 A 的各个元素,保证不重复。如果 A 是空集,则这一行没有数字。
第三行一个整数 y(0≤y≤63),表示集合 B 的元素个数。
第四行 y 个整数 b1,...bx,表示集合 B 的各个元素,保证不重复。如果 B 是空集,则这一行没有数字。
输出格式
输出三行。
第一行输出一个整数,表示 ∣A∣。
第二行输出若干个整数,表示 A∩B 中对应元素,从小到大输出,用空格隔开。如果是空集,则这一行什么也不输出,保留换行。
第三行输出若干个整数,表示 A∪B 中对应元素,从小到大输出,用空格隔开。如果是空集,则这一行什么也不输出,保留换行。
输入输出样例
输入 #1
4 1 3 5 8 3 3 6 8
输出 #1
4 3 8 1 3 5 6 8
输入 #2
04 1 2 3 4
输出 #2
01 2 3 4
题解
使用set的方法有很多种,根据这道题目的要求可以做出以下输出
循环,如果读到了一个数,就将 a 数组对应的元素标记为 1
循环,如果读到了一个数,就将 b 数组对应的元素标记为 1
循环,i 从 0 到 63,输出 A 和 B 的交集
如果 i 同时在集合 A 和 B 中,说明它是 A∩B 的元素。
循环,i 从 0 到 63,输出 A 和 B 的并集
如果 i 在集合 A 或 B 至少一个集合,说明它是 A∪B 的元素。
代码
#include<iostream>
using namespace std;
int a[65], b[65], x, y, tmp;
int main() {// 读入 xcin >> x;for (int i = 0; i < x; i++) {cin >> tmp;a[tmp] = 1; // 将集合 A 对应的元素标记为 1}int sizeA = 0; // 集合 A 的大小// 循环,i 从 0 到 64,计算集合 A 的大小for (int i = 0; i < 65; i++) {if (a[i] == 1) {sizeA++;}}cout<<sizeA<<endl;// 读入 ycin >> y;for (int i = 0; i < y; i++) {cin >> tmp;b[tmp] = 1; // 将集合 B 对应的元素标记为 1}// 循环,i 从 0 到 63,输出 A 和 B 的交集for (int i = 0; i < 63; i++) {if (a[i] == 1 && b[i] == 1) {cout << i << " "; // 输出交集元素}}cout << endl;// 循环,i 从 0 到 63,输出 A 和 B 的并集for (int i = 0; i < 63; i++) {if (a[i] == 1 || b[i] == 1) {cout << i << " "; // 输出并集元素}}return 0;
}相关文章:

C++set集合与并查集map映射,哈希表应用实例B3632 集合运算 1P1918 保龄球
集合的性质 无序性互异性确定性 B3632 集合运算 1 题面 题目背景 集合是数学中的一个概念,用通俗的话来讲就是:一大堆数在一起就构成了集合。 集合有如下的特性: 无序性:任一个集合中,每个元素的地位都是相同的&…...
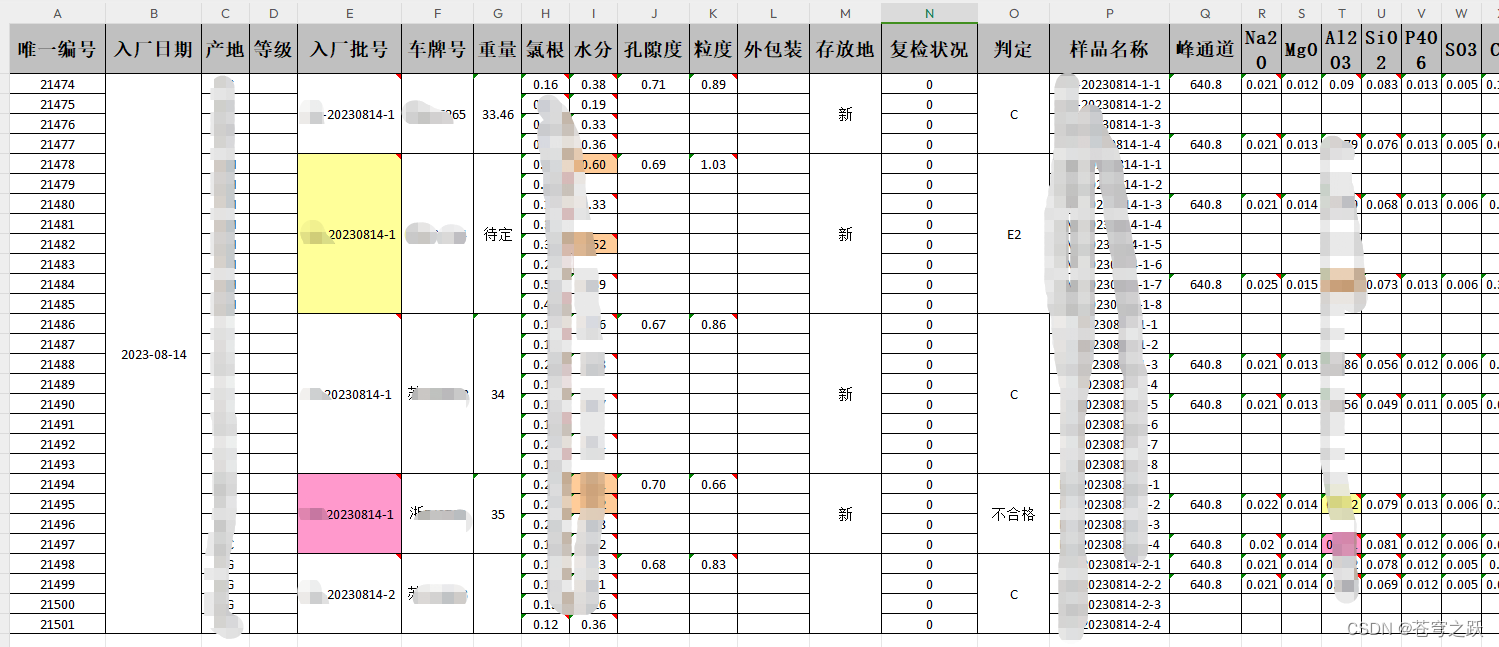
easyexcel合并单元格底色
一、效果图 二、导出接口代码 PostMapping("selectAllMagicExport")public void selectAllMagicExport(HttpServletRequest request, HttpServletResponse response) throws IOException {ServiceResult<SearchResult<TestMetLineFe2o3Export>> result …...

OpenCV图片校正
OpenCV图片校正 背景几种校正方法1.傅里叶变换 霍夫变换 直线 角度 旋转3.四点透视 角度 旋转4.检测矩形轮廓 角度 旋转参考 背景 遇到偏的图片想要校正成水平或者垂直的。 几种校正方法 对于倾斜的图片通过矫正可以得到水平的图片。一般有如下几种基于opencv的组合方…...
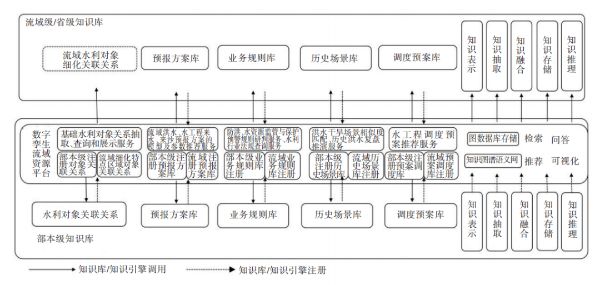
数字孪生流域共建共享相关政策解读
当前数字孪生技术在水利方面的应用刚起步,2021年水利部首次提出“数字孪生流域”概念,即以物理流域为单元、时空数据为底座、数学模型为核心、水利知识为驱动,对物理流域全要素和水利治理管理活动全过程的数字映射、智能模拟、前瞻预演&#…...
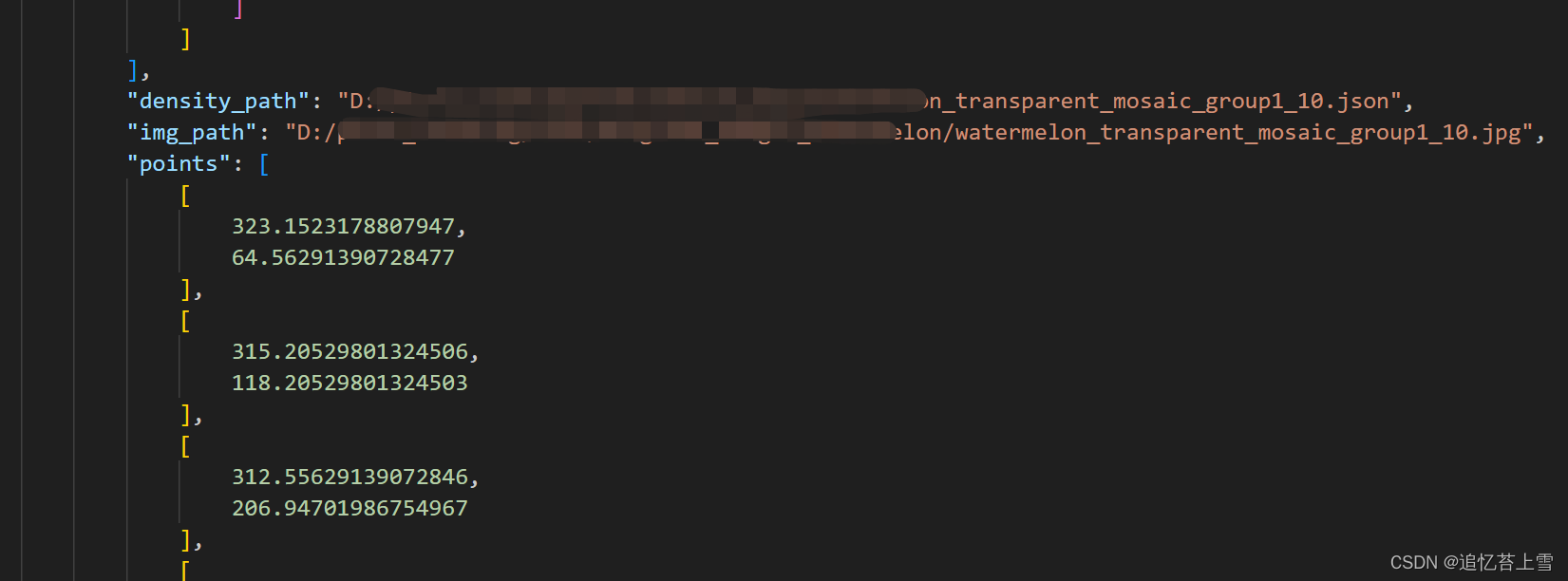
FSC147数据集格式解析
一. 引言 在研究很多深度学习框架的时候,往往需要使用到FSC147格式数据集,若要是想在自己的数据集上验证深度学习框架,就需要自己制作数据集以及相关标签,在论文Learning To Count Everything中,该数据集首次被提出。 …...

el-element中el-tabs案例的使用
el-element中el-tabs的使用 代码呈现 <template><div class"enterprise-audit"><div class"card"><div class"cardTitle"><p>交易查询</p></div><el-tabs v-model"activeName" tab-cl…...

tomcat结构目录有哪些?
bin 启动,关闭和其他脚本。这些 .sh文件(对于Unix系统)是这些.bat文件的功能副本(对于 Windows系统)。由于Win32命令行缺少某些功能,因此此处包含一些其他文件。 比如说:windows下启动tomcat用的…...

生成式AI系列 —— DCGAN生成手写数字
1、模型构建 1.1 构建生成器 # 导入软件包 import torch import torch.nn as nnclass Generator(nn.Module):def __init__(self, z_dim20, image_size256):super(Generator, self).__init__()self.layer1 nn.Sequential(nn.ConvTranspose2d(z_dim, image_size * 32,kernel_s…...

vscode-vue项目格式化+语法检验-草稿
Vue学习笔记7 - 在Vscode中配置Vetur,ESlint,Prettier_vetur规则_Myron.Maoyz的博客-CSDN博客...

【Java从0到1学习】10 Java常用类汇总
1. System类 System类对读者来说并不陌生,因为在之前所学知识中,需要打印结果时,使用的都是“System.out.println();”语句,这句代码中就使用了System类。System类定义了一些与系统相关的属性和方法,它所提供的属性和…...

第三届人工智能与智能制造国际研讨会(AIIM 2023)
第三届人工智能与智能制造国际研讨会(AIIM 2023) The 3rd International Symposium on Artificial Intelligence and Intelligent Manufacturing 第三届人工智能与智能制造国际研讨会(AIIM 2023)将于2023年10月27-29日在成都召开…...

层次分析法
目录 一:问题的引入 二:模型的建立 1.分析系统中各因素之间的关系,建立系统的递阶层次结构。 2.对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。 3.由判…...

Error Handling
有几个特定的异常类允许用户代码对与CAN总线相关的特定场景做出反应: Exception (Python standard library)+-- ...+-- CanError (python-can)+-- CanInterfaceNotImplementedError+-- CanInitializationError...
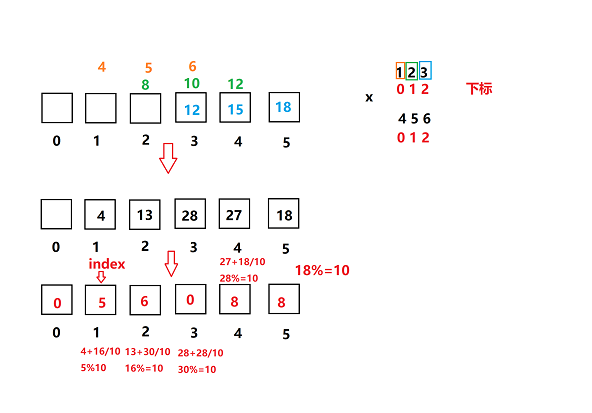
leetcode:字符串相乘(两种方法)
题目: 给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。 注意:不能使用任何内置的 BigInteger 库或直接将输入转换为整数。 示例 1: 输入: num1 "2", nu…...
【爬虫练习之glidedsky】爬虫-基础2
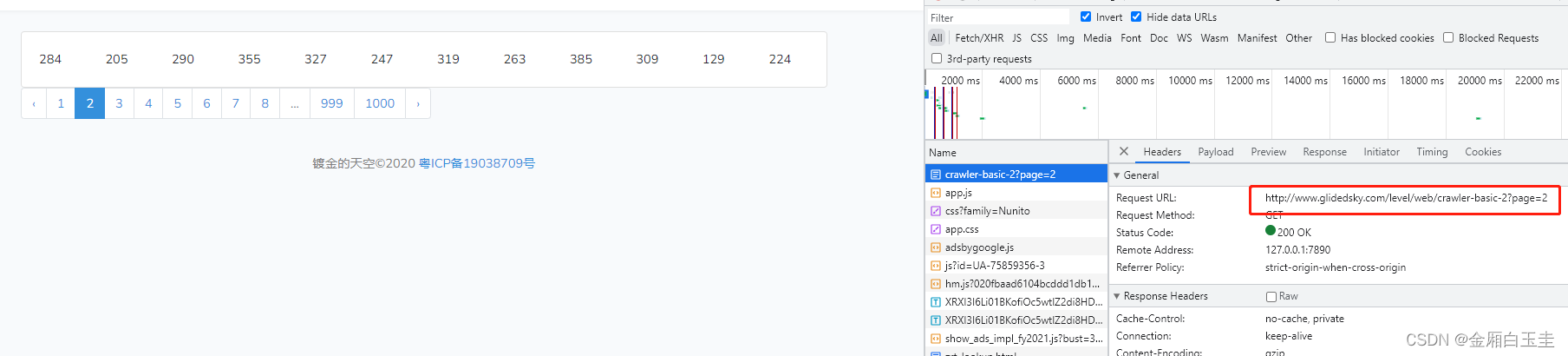
题目 链接 爬虫往往不能在一个页面里面获取全部想要的数据,需要访问大量的网页才能够完成任务。 这里有一个网站,还是求所有数字的和,只是这次分了1000页。 思路 找到调用接口 可以看到后面有个参数page来控制页码 代码实现 import reques…...

03.有监督算法——决策树
1.决策树算法 决策树算法可以做分类,也可以做回归 决策树的训练与测试: 训练阶段:从给定的训练集构造出一棵树(从根节点开始选择特征,如何进行特征切分) 测试阶段:根据构造出来的树模型从上…...
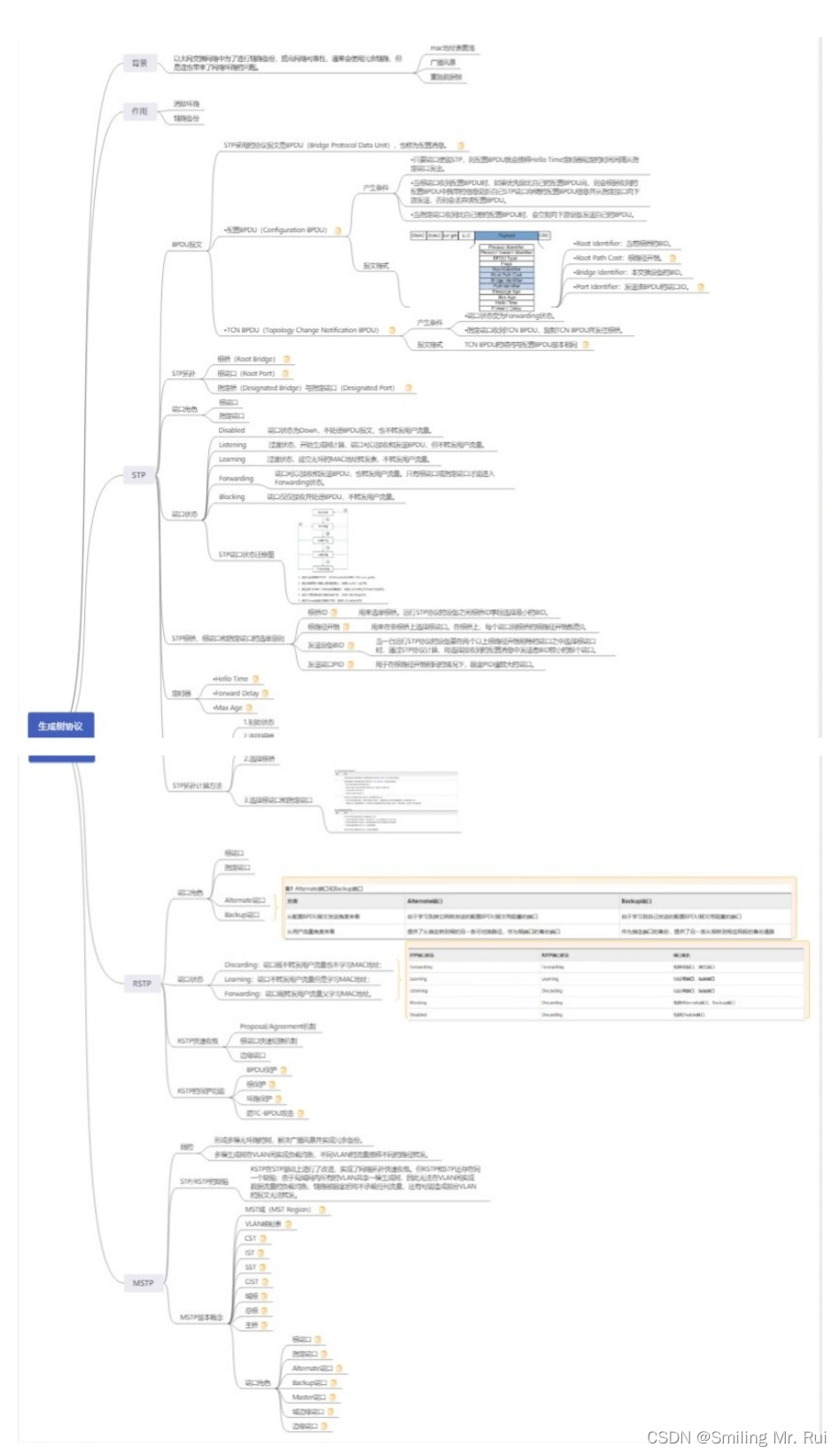
网络协议详解之STP
目录 一、STP协议(生成树) 1.1 生成树协议核心知识点: 1.2 生成树协议与导致问题: 生成树含义: 1.3 802.1D 规则: 802.1D 缺点: 1.4 PVST cisco私有 1.5 PVST 1.6 快速生成树 快速的原…...
Eltima USB Network Gate 10.0 Crack
USB Network Gate -通过网络共享USB 设备 USB Network Gate (前身为以太网USB控制器USB) 轻松的通过网络(Internet/LAN/WAN)分享您的一个或者多个连接到您计算机的USB设备。 无论您身处异国还是近在隔壁办公室,您都可以轻松使用远程扫描仪、打印机、摄像头、调制解…...
)
SpringCloudGateway网关实战(一)
SpringCloudGateway网关实战(一) 目前对cloud的gateway功能还是不太熟悉,因此特意新建了对应的应用来尝试网关功能。 网关模块搭建 首先我们新建一个父模块用于添加对应的springboot依赖和cloud依赖。本模块我们的配置读取使用的是nacos&a…...
django中使用ajax发送请求
1、ajax简单介绍 浏览器向网站发送请求时 是以URL和表单的形式提交的post 或get 请求,特点是:页面刷新 除此之外,也可以基于ajax向后台发送请求(异步) 依赖jQuery 编写ajax代码 $.ajax({url: "发送的地址"…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
