最大公约数和最小公倍数
最大公约数:
概念:
公约数中最大的称为最大公约数。 对任意的若干个正整数,1总是它们的公因数。 公约数与公倍数相反,就是既是A的约数同时也是B的约数的数,12和15的公约数有1,3,最大公约数就是3。
代码思路:
采取辗转相除法——如果 a 和 b 是两个正整数,且 a>b ,则a和b的最⼤公约数等于 b 和 a%b ( a 除以 b 所得的余数)的最⼤公约数。
通过辗转相除法的原理,我们可以明白,在此处可能需要使用while的循环进行运算。
而循环的条件则是进入循环的二者能够进行完全的整除,那么便得到了最大公约数。
代码展示:
#include <stdio.h>
int main()
{int m = 0;int n = 0;scanf("%d %d", &m, &n);//18 24//辗转相除法int k = 0;//当n不能整除m,即k≠0,更新两个最值重复步骤计算n与m%n的最⼤公约数while (k = m % n){m = n;n = k;}printf("%d\n", n);return 0;
}
最小公倍数:
概念:
指在两个或两个以上的自然数中,如果它们有相同的倍数,这些倍数就是它们的公倍数,其中除0以外最小的一个公倍数,叫做这几个数的最小公倍数。
代码思路:
可以利用最小公倍数和最大公约数之间的关系——最⼩公倍数可以由两数乘积除以两数的最⼤公约数求得。
因此,我们可以先使用辗转相除法求出最大公约数,在将两个数相乘,得到的积在除取最大公约数,因此得到最小公倍数。
代码演示:
#include <stdio.h>
int main()
{int m = 0;int n = 0;//输⼊scanf("%d %d", &m, &n);//18 24int k = 0;int mul = m*n;//辗转相除法求得最⼤公约数while (k = m % n){m = n;n = k;}printf("%d\n", mul/n);return 0;
}相关文章:

最大公约数和最小公倍数
最大公约数: 概念: 公约数中最大的称为最大公约数。 对任意的若干个正整数,1总是它们的公因数。 公约数与公倍数相反,就是既是A的约数同时也是B的约数的数,12和15的公约数有1,3,最大公约数就是…...
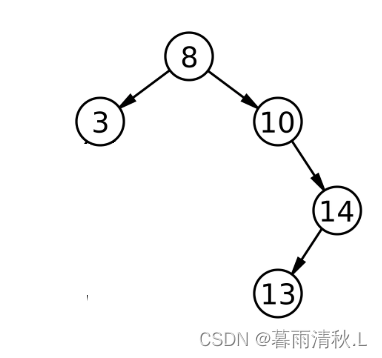
数据结构——二叉搜索树(附带C++实现版本)
文章目录 二叉搜索树概念 二叉树的实际应用二叉树模拟实现存储结构二叉搜索树构成二叉搜索树的查找插入操作中序遍历二叉树的删除循环(利用左子树最右节点)递归(利用右子树根节点) 二叉树拷贝二叉树资源的销毁 二叉树实现完整代码总结 二叉搜索树 概念 二叉搜索树…...
C++对C的扩展Extension)
C++(3)C++对C的扩展Extension
类型增强 1、类型更加严格 不初始化,无法通过编译;C不初始化,则随机赋值 #include <iostream> #include <stdlib.h>int main() {const int a 100; //真正的const,无法修改 // int *p &a; 报错const int *p…...
使用GitHub账号、Copilot异常)
在vscode(idea)使用GitHub账号、Copilot异常
在idea使用GitHub账号、Copilot异常 登录GitHub显示 Invalid authentication data.Connection refused: connect或者副驾驶显示 Failed to initiate the GitHub login process. Please try again.一般网上的方法推荐使用token登录,或者降级副驾驶 经过研究&#x…...

新的后端渲染:服务器驱动UI
通过API发送UI是一种彻底的新方法,将改变传统的UI开发。 一项正在改变我们对用户界面 (UI) 的看法的技术是通过 API 发送 UI,也称为服务器驱动UI。这种方法提供了新水平的活力和灵活性,正在改变 UI 开发的传统范例。 服务器驱动 UI 不仅仅是…...

Postman如何做接口自动化测试?
前言 什么是自动化测试 把人对软件的测试行为转化为由机器执行测试行为的一种实践。 例如GUI自动化测试,模拟人去操作软件界面,把人从简单重复的劳动中解放出来。 本质是用代码去测试另一段代码,属于一种软件开发工作,已经开发完…...

excel文本函数篇2
本期主要介绍LEN、FIND、SEARCH以及后面加B的情况: (1)后缀没有B:一个字节代表一个中文字符 (2)后缀有B:两个字节代表一个中文字符 1、LEN(text):返回文本字符串中的字符个数 2、…...
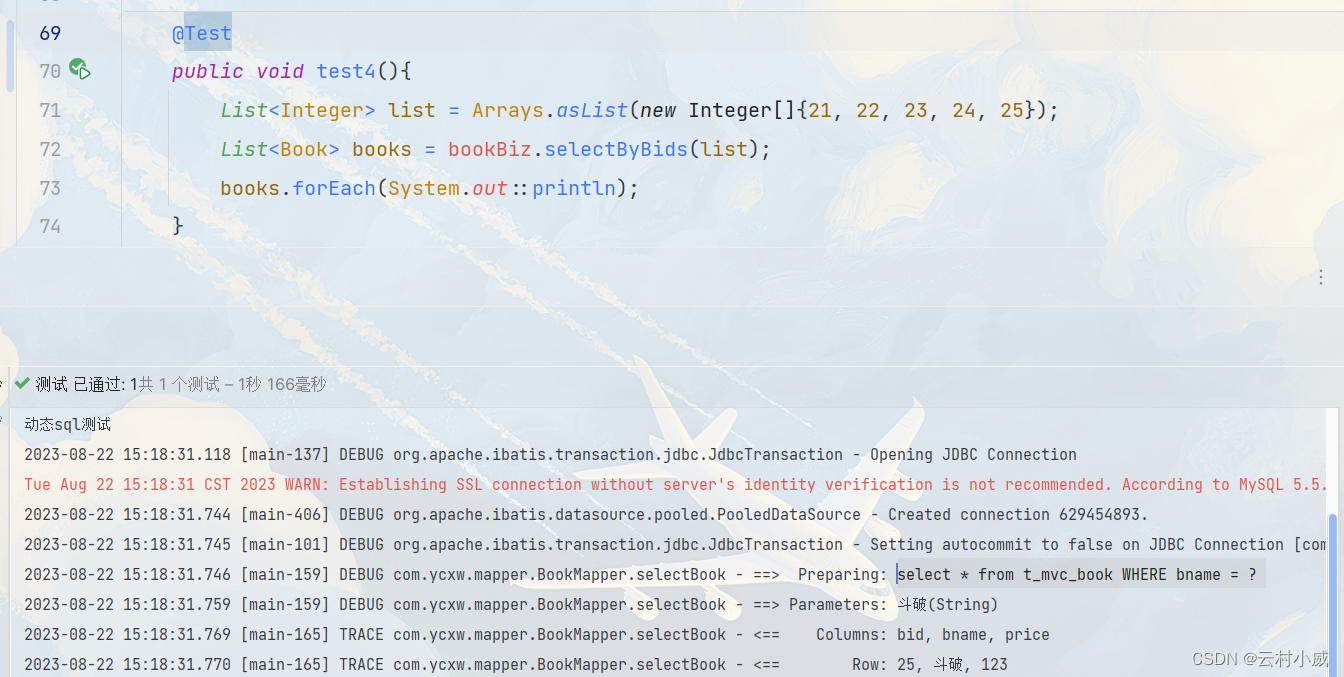
【MyBatis】动态SQL > 重点:${...}和#{...}与resultMap和resultType的区别
目录 一、MyBatis动态sql 1.1 动态sql的作用 1.2 动态sql作用论证 1.2.1 条件判断:<if> 1.2.2 循环迭代:<foreach> 1.2.3 SQL片段重用 1.2.4 动态条件组合:<choose><when><otherwise> 1.2.5 <where…...

什么是BEM命名规范?为什么要使用BEM命名规范?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ BEM命名规范⭐ 为什么使用BEM命名规范?⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为…...

JavaScript:交集和差集的应用场景
在集合A和集合B中,属于集合A,同时也属于集合B的元素组成的集合,就是交集。 在A中所有不属于集合B元素,组合成集合,就是差集。 那么在平时的开发中,如何使用差集和交集来解决问题呢? 现在有这…...
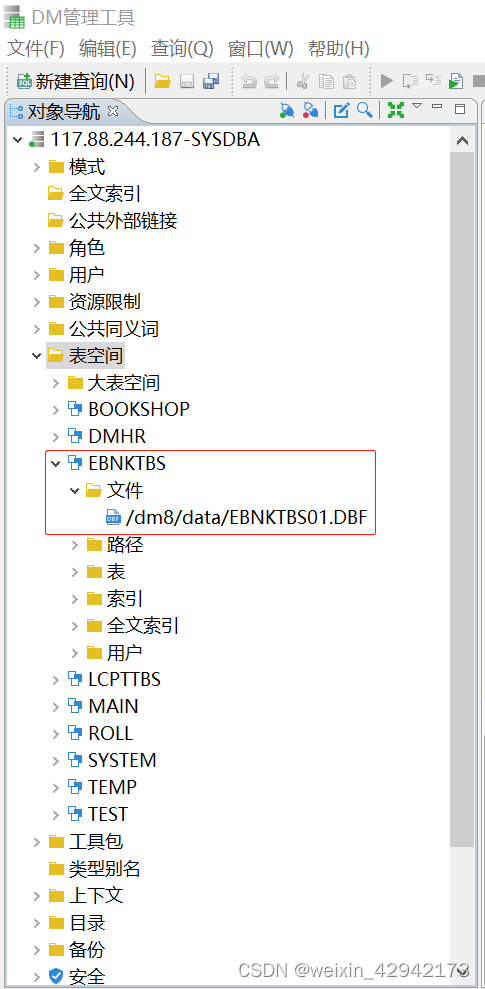
达梦数据库表空间创建和管理
概述 本文将介绍在达梦数据库如何创建和管理表空间。 1.创建表空间 1.1表空间个数限制 理论上最多允许有65535个表空间,但用户允许创建的表空间 ID 取值范围为0~32767, 超过 32767 的只允许系统使用,ID 由系统自动分配,ID不能…...

三、MySQL 数据库安装集
一、CentOS—YUM 1. MySQL—卸载 # 1、查看存在的MySQL。 rpm -qa | grep -i mysql rpm -qa | grep mysql# 2、删除存在的MySQL。 rpm -e –-nodeps 包名# 3、查找存在的MySQL目录。 find / -name mysql# 4、删除存在的MySQL目录。 rm -rf 目录# 5、删除存在的MySQL配置文件。…...
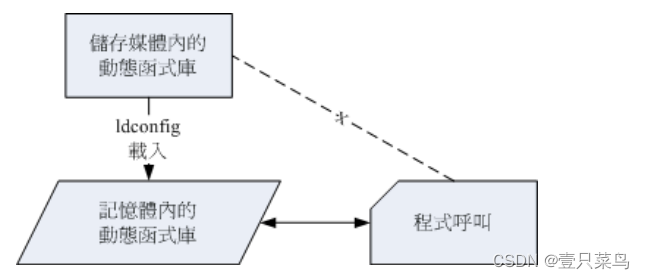
【BASH】回顾与知识点梳理(三十九)
【BASH】回顾与知识点梳理 三十九 三十九. make、tarball、函数库及软件校验39.1 用 make 进行宏编译为什么要用 makemakefile 的基本语法与变量 39.2 Tarball 的管理与建议使用原始码管理软件所需要的基础软件Tarball 安装的基本步骤一般 Tarball 软件安装的建议事项 (如何移除…...

蓝蓝设计-UI设计公司案例-HMI列车监控系统界面设计解决方案
2013年,为加拿大庞巴迪(Bombardier)设计列车监控系统界面设计。 2015-至今,为中车集团旗下若干公司提供HMI列车监控系统界面设计,综合考虑中车特点、城轨车、动车组的不同需求以及HMI硬键屏和触摸 屏的不同操作方式,重构框架设计、交互设计、…...

Blazor前后端框架Known-V1.2.13
V1.2.13 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazo…...

vue 复制文本
一个常用的库就是 clipboard.js,它可以帮助您实现跨浏览器的复制到剪贴板功能 首先,安装 clipboard.js: cnpm install clipboard 创建一个 Vue 组件并使用 clipboard.js: <template><div><input v-model"…...
西瓜书第三章
广义线性模型 考虑单点可微函数 g ( ⋅ ) g(\cdot) g(⋅),令 y g − 1 ( ω T x b ) yg^{-1}(\omega^{T}xb) yg−1(ωTxb),这样得到的模型称为“广义线性模型”,其中函数 g ( ⋅ ) g(\cdot) g(⋅)称为“联系函数”。显然,对数线…...

关于python如何使用sqlalchemy连接sap_hana数据库
1.先安装sqlalchemy pip install sqlalchemy 2.from sqlalchemy import create_engine 3.创建数据库连接方式: 假设数据连接方式如下: usernameH_TEOPT passwordww122222 jdbcUrljdbc:sap://192.163.1.161:21681/?currentschema 那么使用sqlalchemy 的…...
)
微信小程序教学系列(5)
微信小程序教学系列 第五章:小程序发布与推广 第一节:小程序发布流程介绍 小伙伴们,欢迎来到第五章的教学啦!在这一章中,我们将一起来探索小程序的发布与推广流程。你准备好了吗?让我们开始吧࿰…...

【计算机网络篇】TCP协议
✅作者简介:大家好,我是小杨 📃个人主页:「小杨」的csdn博客 🐳希望大家多多支持🥰一起进步呀! TCP协议 1,TCP 简介 TCP(Transmission Control Protocol)是…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

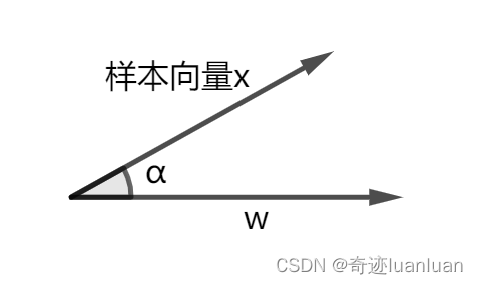
向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
