刷题记录:牛客NC54585小魂和他的数列 [线段树卡常,真恶心]
传送门:牛客
题目描述:
一天,小魂正和一个数列玩得不亦乐乎。
小魂的数列一共有n个元素,第i个数为Ai。
他发现,这个数列的一些子序列中的元素是严格递增的。
他想知道,这个数列一共有多少个长度为K的子序列是严格递增的。
请你帮帮他,答案对998244353取模。
对于100%的数据,1≤ n ≤ 500,000,2≤ K ≤ 10,1≤ Ai ≤ 109。
输入:
5 3
2 3 3 5 1
输出:
2
前置提要:本题卡线段树常数,十分恶心,本人试了几次卡常,只能优化到85分
首先看到题面,我们会发现这是一个比较清明的dpdpdp题.我们设dp[i][j]dp[i][j]dp[i][j]为以iii位置结尾长度为jjj的子序列的的个数.那么对于当前的i,ji,ji,j来说,我们的需要找到前i−1i-1i−1个位置中每一个dp[k][j−1]k∈[1,i−1]&&a[k]<a[i]dp[k][j-1] \quad k\in[1,i-1] \&\& a[k]<a[i]dp[k][j−1]k∈[1,i−1]&&a[k]<a[i]然后进行累加,此时如果我们直接使用forforfor进行枚举会发现时间复杂度是不对的.此时复杂度达到了n∗k∗lognn*k*lognn∗k∗logn所以我们需要进行优化
我们可以用线段树树状数组来维护这个题目.开kkk个线段树树状数组来维护i−1i-1i−1之前所有位置子序列长度为lenlen∈[1,k]len \quad len\in[1,k]lenlen∈[1,k]的子序列个数.那么对于我们现在的dp[i][j]dp[i][j]dp[i][j]来说,dp[i][j]=query(j−1,1,i−1)参数(id,l,r)dp[i][j]=query(j-1,1,i-1) \quad 参数(id,l,r)dp[i][j]=query(j−1,1,i−1)参数(id,l,r).用ansansans累加一下即可
本题需要进行离散化操作
下面是本人优化到平常极限的线段树代码(85分):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 500100
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,sum;
}tree[11][maxn*4];
const int mod=998244353;
inline void update(int id,int pos,int v,int l,int r,int rt) {if(l==pos&&r==pos) {tree[id][rt].sum=(tree[id][rt].sum+v)%mod;return ;}int mid=(l+r)>>1;if(pos<=mid) update(id,pos,v,l,mid,ls);else update(id,pos,v,mid+1,r,rs);tree[id][rt].sum=(tree[id][ls].sum+tree[id][rs].sum)%mod;
}
inline int query(int id,int l,int r,int L,int R,int rt) {if(L==l&&R==r) return tree[id][rt].sum;int mid=(L+R)>>1;if(r<=mid) return query(id,l,r,L,mid,ls);else if(l>mid) return query(id,l,r,mid+1,R,rs);else return (query(id,l,mid,L,mid,ls)+query(id,mid+1,r,mid+1,R,rs))%mod;
}
int n,k;int a[maxn];
int v[maxn];
int main() {n=read();k=read();for(int i=1;i<=n;i++){a[i]=read();v[i-1]=a[i];}sort(v,v+n);int Size=unique(v,v+n)-v;int ans=0;for(int i=1;i<=n;i++) {int x=lower_bound(v,v+Size,a[i])-v+1;update(1,x,1,1,Size,1);if(x-1==0) continue;for(int j=2;j<=k;j++) {if(j-1>i) continue;int sum=query(j-1,1,x-1,1,Size,1);if(j==k) ans=(ans+sum)%mod;update(j,x,sum,1,Size,1);}}cout<<ans<<endl;return 0;
}
下面是可以AC本题的树状数组代码(等我去学完立马补上,博主已简单过了一遍):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
const int mod=998244353;
inline int lowbit(int x) {return x&(~x+1);
}
int n,k;int a[maxn];int sum[11][maxn];
vector<int>v;
void add(int id,int pos,int v) {while(pos<=n) {sum[id][pos]=(sum[id][pos]+v)%mod;pos+=lowbit(pos);}
}
int query(int id,int pos) {int ans=0;while(pos) {ans=(ans+sum[id][pos])%mod;pos-=lowbit(pos);}return ans;
}
int main() {n=read();k=read();for(int i=1;i<=n;i++) {a[i]=read();v.push_back(a[i]);}sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int ans=0;for(int i=1;i<=n;i++) {int x=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1;add(1,x,1);for(int j=2;j<=k;j++) {int sum=query(j-1,x-1);if(j==k) ans=(ans+sum)%mod;add(j,x,sum);}}cout<<ans<<endl;return 0;
}
相关文章:

刷题记录:牛客NC54585小魂和他的数列 [线段树卡常,真恶心]
传送门:牛客 题目描述: 一天,小魂正和一个数列玩得不亦乐乎。 小魂的数列一共有n个元素,第i个数为Ai。 他发现,这个数列的一些子序列中的元素是严格递增的。 他想知道,这个数列一共有多少个长度为K的子序列是严格递增的。 请你帮…...

2019蓝桥杯真题旋转 C语言/C++
题目描述 图片旋转是对图片最简单的处理方式之一,在本题中,你需要对图片顺时针旋转 90 度。 我们用一个 nm 的二维数组来表示一个图片,例如下面给出一个 34 的 图片的例子: 1 3 5 7 9 8 7 6 3 5 9 7 这个图片顺时针旋转 90 度…...
<JVM上篇:内存与垃圾回收篇>11 - 垃圾回收相关算法
对象存活判断 在堆里存放着几乎所有的 Java 对象实例,在 GC 执行垃圾回收之前,首先需要区分出内存中哪些是存活对象,哪些是已经死亡的对象。只有被标记为己经死亡的对象,GC 才会在执行垃圾回收时,释放掉其所占用的内存…...
狂飙Linux平台,软件部署大全
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
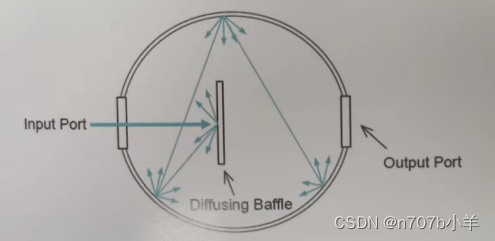
积分球原理及积分球类型介绍
标题积分球标准型积分球LED积分球均匀光源便携式高亮度积分球均匀光源微光积分球均匀光源积分球均匀光源iSphere高光谱响应光学积分球其他分类积分球 积分球原理:由于球体内整涂有白色漫反射材料的空腔球体,球壁上开有采样口,当待测样品光源进入积分球的…...

Vision Transformer(ViT) 2: 应用及代码讲解
文章目录1. 代码讲解1.1 PatchEmbed类1)__init__ 函数2) forward 过程1.2 Attention类1)__init__ 函数2)forward 过程1.3 MLP类1)__init__ 函数2)forward函数1.4 Block类1)__init__ 函数2)forwa…...
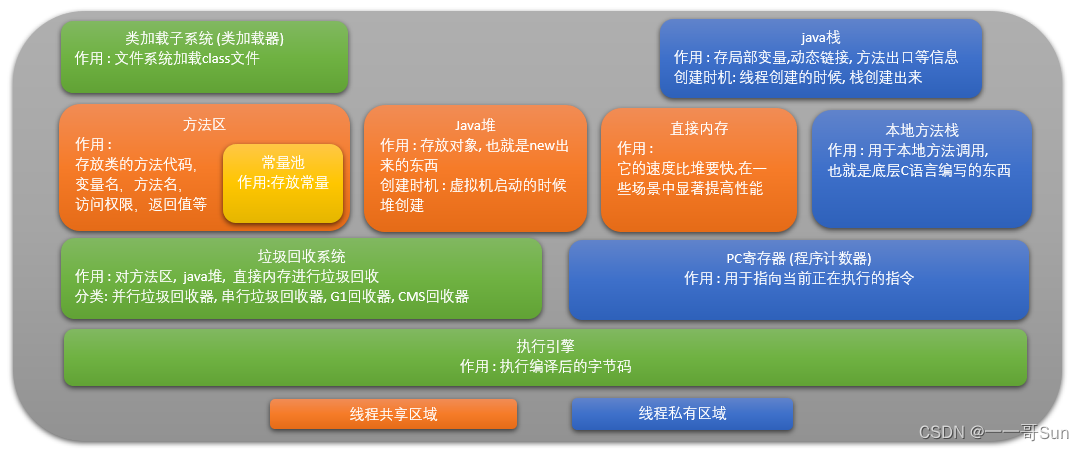
高频面试题|JVM虚拟机的体系结构是什么样的?
一. 前言最近有很多小伙伴都在找工作,他们在面试时经常被面试官问到一个问题:请说说JVM虚拟机的体系结构是什么样的?很多小伙伴都能说出堆、栈等相关内容,但面试官紧接着又问,你还知道其他内容吗?这时不少小伙伴就语塞…...
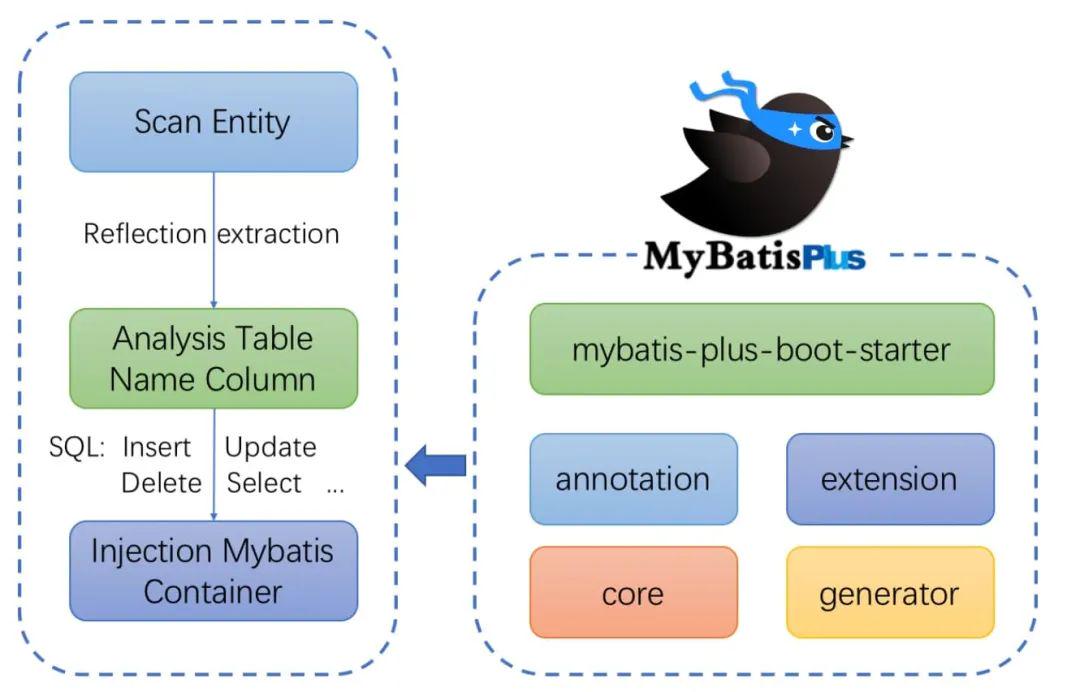
MyBatis-Plus详细讲解(整合spring Boot)
哈喽,大家好,今天带大家了解的是MyBatis-Plus(简称 MP),是一个 MyBatis 的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。首先说一下MyBatis-Plus的愿景是什么&…...

骨传导耳机是不是智商税?骨传导耳机真的不伤耳吗?
很多人对骨传导耳机是具有一定的了解,但是对骨传导耳机还是有一定的刻板印象,那么骨传导耳机到底是不是智商税呢?主要还是要从骨传导耳机传声原理上讨论。 骨传导耳机是属于固体传声的一种方式,通过骨骼传递声音,在使用…...
模拟实现string
目录 1、基本成员变量 2、默认成员函数 构造函数 析构函数 拷贝构造函数(深拷贝) 赋值运算符重载 3、容量与大小相关的函数 size capacity 4、字符串访问相关函数 operator [ ]重载 迭代器 5、增加的相关函数 reserve扩容 resize push_back追加字符 appe…...
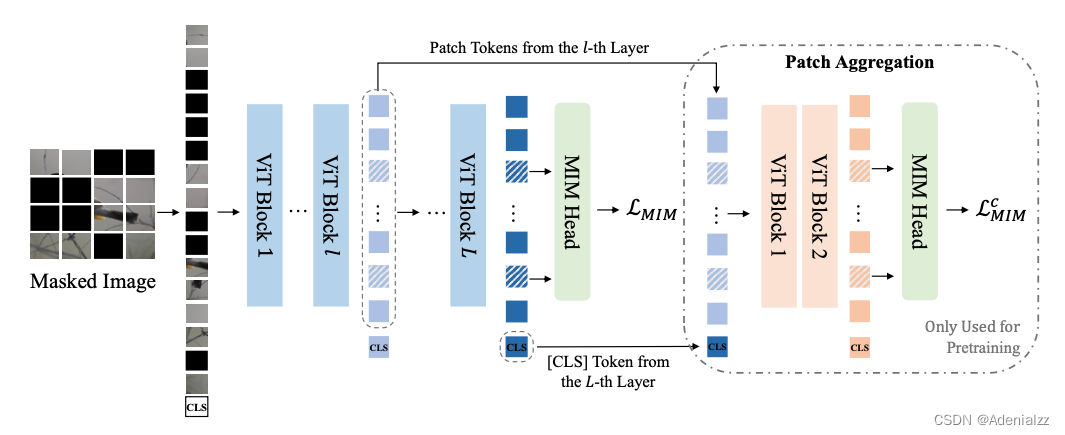
自监督表征预训练之掩码图像建模
自监督表征预训练之掩码图像建模 前言 目前,在计算机视觉领域,自监督表征预训练有两个主流方向,分别是对比学习(contrastive learning)和掩码图像建模(masked image modeling)。两个方向在近几…...
| 代码+思路+重要知识点)
华为OD机试题 - 磁盘容量(JavaScript)| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 使用说明 参加华为od机试,一定要注意不要完全背…...

ChatGPT:“抢走你工作的不会是 AI ,而是先掌握 AI 能力的人”
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! ChatGPT:“抢走你工作的不会是 AI ,而是先掌握 AI 能力的人” ChatGPT:美国OpenAI 研发的聊天机器人程序,人工智能技术…...

数据结构与算法(Java版) | 线性结构和非线性结构
之前,我们说过,数据结构是算法的基础,因此接下来在这一讲我就要来给大家重点介绍一下数据结构了。 首先,大家需要知道的是,数据结构包括两部分,即线性结构和非线性结构。知道这点之后,接下来我…...
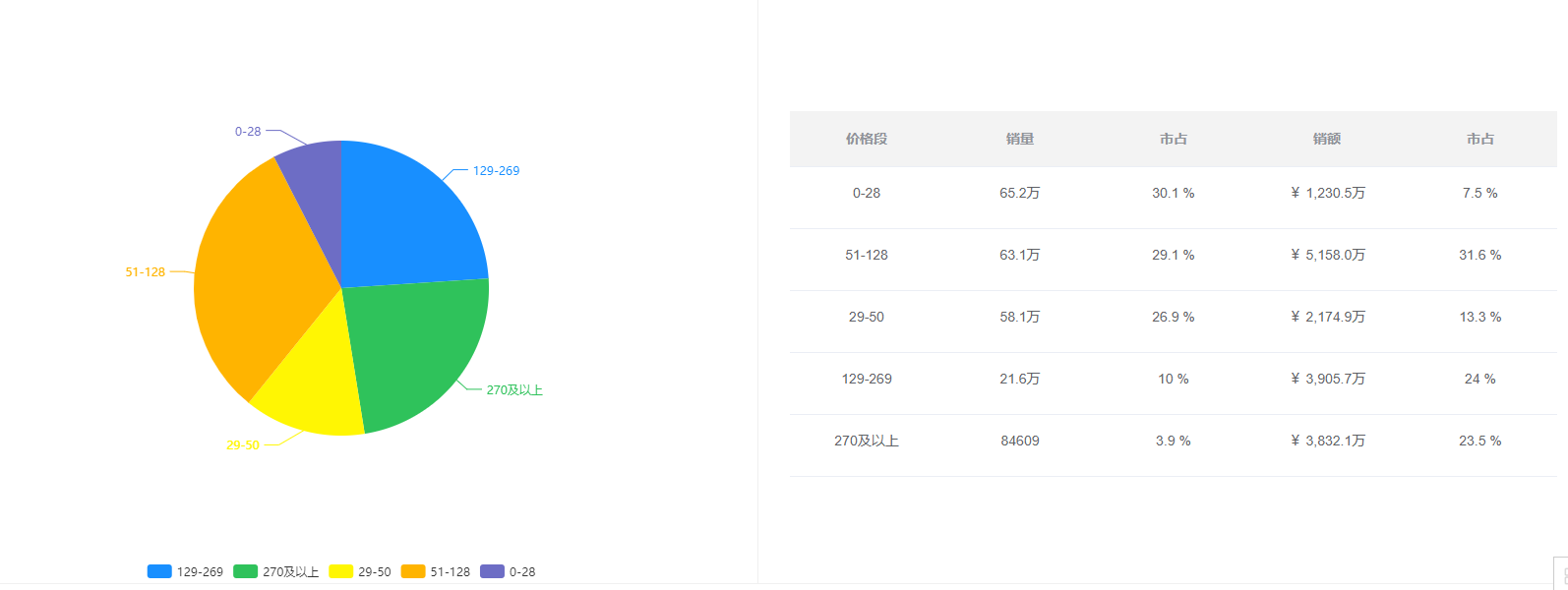
电商数据查询平台:母婴行业妈妈用品全网热销,头部品牌格局初现
以往,奶粉、纸尿裤这类产品基本就代表了整体母婴市场中的消费品。而如今,随着母婴行业的高速发展和消费升级,母婴商品的种类日益丰富,需求也不断深入。 在京东平台,母婴大品类中除了包含婴童相关的食品(奶粉…...
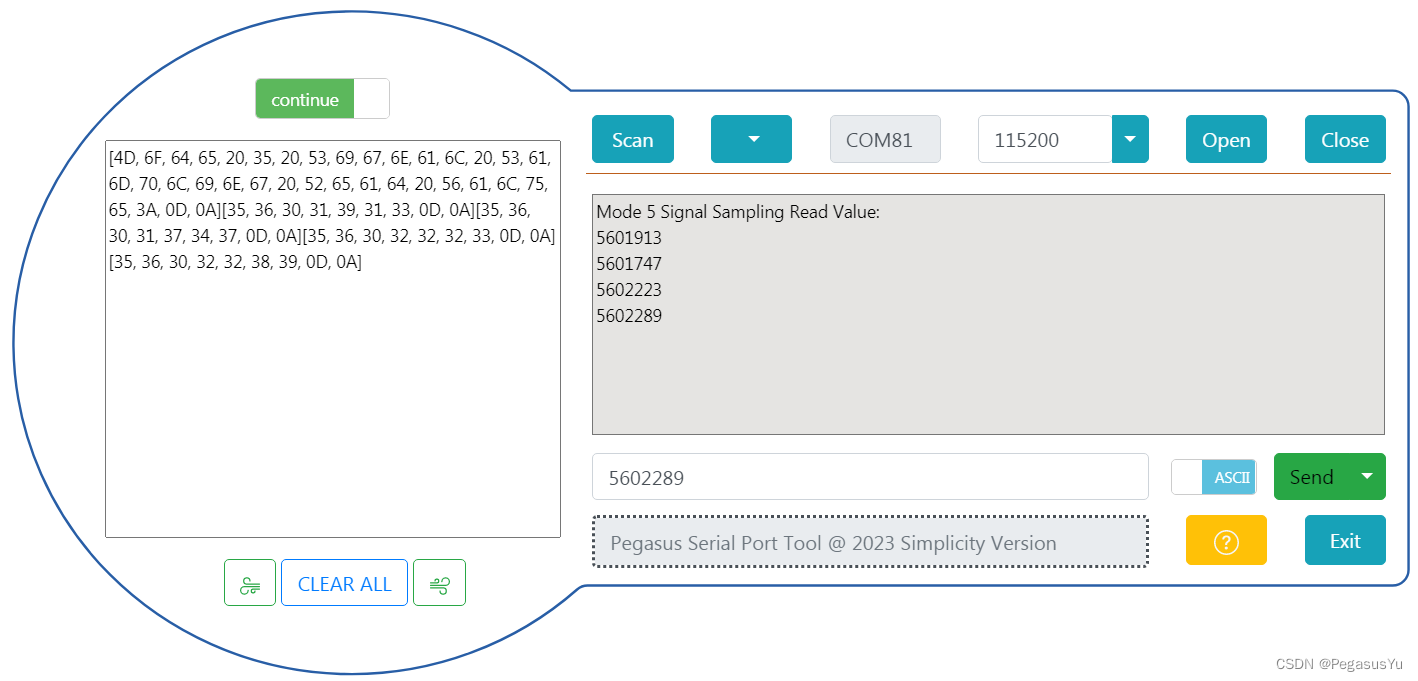
STM32模拟SPI协议获取24位模数转换(24bit ADC)芯片AD7791电压采样数据
STM32模拟SPI协议获取24位模数转换(24bit ADC)芯片AD7791电压采样数据 STM32大部分芯片只有12位的ADC采样性能,如果要实现更高精度的模数转换如24位ADC采样,则需要连接外部ADC实现。AD7791是亚德诺(ADI)半导体一款用于低功耗、24…...
| 代码+思路+重要知识点)
华为OD机试题 - 交换字符(JavaScript)| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 字符串加密(JavaScript) 华为OD机试题 - 字母消消乐(JavaScript) 华为OD机试题 - 字母计数(JavaScript) 华为OD机试题 - 整数分解(JavaScript) 华为OD机试题 - 单词反转(JavaScript) 使用说明 参加华为od机试,一定要注意不要完全背…...

最好的工程师像投资者一样思考,而不是建设者
我在大学期间住在图书馆。“我学习的教科书理论越多,我就会成为一名更好的工程师,”我想。然而,当我开始工作时,我注意到业内最优秀的工程师并不一定比应届毕业生了解更多的理论。他们只是带来了不同的心态,即投资者的…...
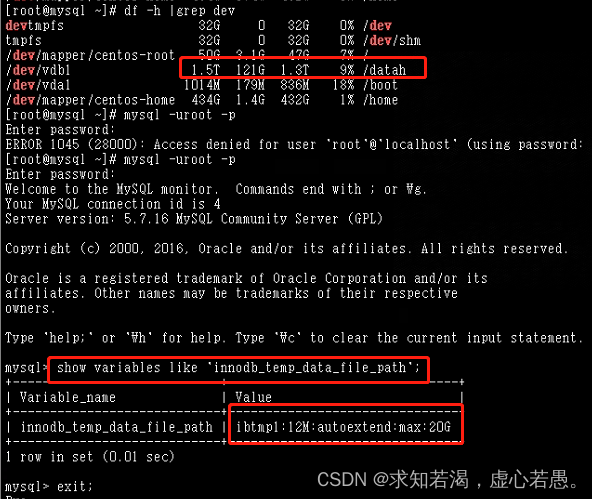
Mysql里的ibtmp1文件太大,导致磁盘空间被占满
目录 一、查看磁盘的时候发现磁盘空间100% 二、 排查的时候:查看是什么文件占用的时候,发现是数据库临时表空间增长的 三、为了避免以后再次出现ibtmp1文件暴涨,限制其大小,需在配置文件加入 四、重启Mysql实例(重启后…...
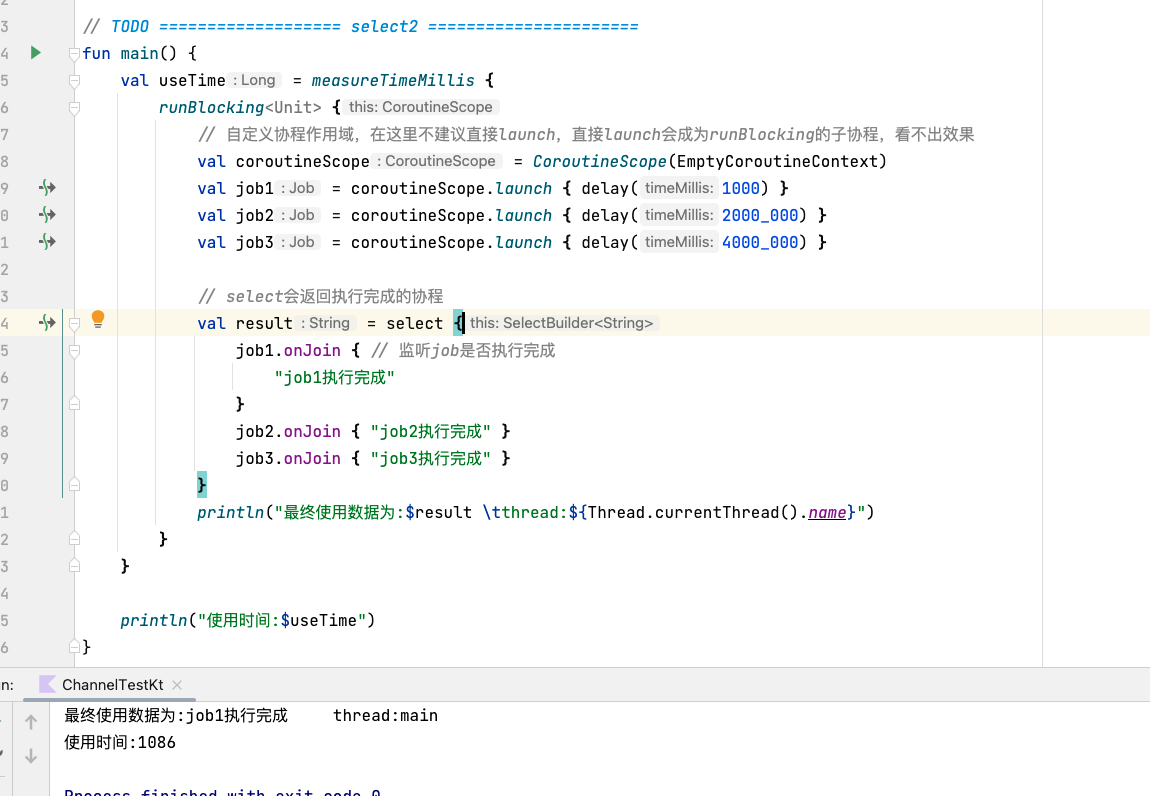
android kotlin 协程(四) 协程间的通信
android kotlin 协程(四) 协程间的通信 学完本篇你将会了解到: channelproduceactorselect 先来通过上一篇的简单案例回顾一下挂起于恢复: fun main() {val waitTime measureTimeMillis {runBlocking<Unit> {println("main start") // 1 // …...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
