车道线检测-PolyLaneNet 论文学习笔记
- 论文:《PolyLaneNet: Lane Estimation via Deep Polynomial Regression》
- 代码:https://github.com/lucastabelini/PolyLaneNet
- 地址:https://arxiv.org/pdf/2004.10924.pdf
- 参考:https://blog.csdn.net/sinat_17456165/article/details/107171888
- 利用 CNN,基于三次曲线拟合车道线
模型的输入与输出
输入
单张车辆前向图
输出
曲线参数 Pj={ak,j}k=0K\mathcal{P}_j=\{a_{k,j}\}^K_{k=0}Pj={ak,j}k=0K、地平线高度 hhh、车道线的存在性 cjc_jcj、车道线起始高度 sjs_jsj(见下图)
其中,曲线参数确定了车道线的形状:
pj(y)=Σk=0Kak,jykp_j(y)=\Sigma^K_{k=0}a_{k,j}y^k pj(y)=Σk=0Kak,jyk
模型结构

backbone + fully connected layer
f(I;θ)=({Pj,sj,cj}j=1Mmax,h)f(I;\theta)=(\{\mathcal{P}_j,s_j,c_j\}^{M_{max}}_{j=1}, h) f(I;θ)=({Pj,sj,cj}j=1Mmax,h)
损失函数
L({Pj},h,{sj},{cj})=WpLp({Pj},{Lj∗})+Ws1MΣjLreg(sj,sj∗)+Wc1MΣjLcls(cj,cj∗)+WhLreg(h,h∗)\begin{aligned} L(\{\mathcal{P}_j\},h,\{s_j\},\{c_j\})&=W_p L_p(\{\mathcal{P}_j\},\{\mathcal{L}^*_j\})\\&+W_s\frac{1}{M}\Sigma_j L_{reg}(s_j,s^*_j)\\&+W_c\frac{1}{M}\Sigma_j L_{cls}(c_j,c^*_j)\\&+W_h L_{reg}(h,h^*) \end{aligned} L({Pj},h,{sj},{cj})=WpLp({Pj},{Lj∗})+WsM1ΣjLreg(sj,sj∗)+WcM1ΣjLcls(cj,cj∗)+WhLreg(h,h∗)
其中,
Lp({Pj},{Lj∗})=Lreg(xj,xj∗)L_p(\{\mathcal{P}_j\},\{\mathcal{L}^*_j\})=L_{reg}(\pmb{x}_j,\pmb{x}^*_j) Lp({Pj},{Lj∗})=Lreg(xj,xj∗)
xj=[x1,j,...,xN,j]\pmb{x}_j=[x_{1,j},\ ...,\ x_{N,j}] xj=[x1,j, ..., xN,j]
xi,j={pj(yi,j∗),if∣pj(yi,j∗)−xi,j∗∣>τloss0,otherwisex_{i,j}=\begin{cases}p_j(y^*_{i,j}),\ \ \ \ if\ |p_j(y^*_{i,j})-x^*_{i,j}|>\tau_{loss}\\ 0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{cases} xi,j={pj(yi,j∗), if ∣pj(yi,j∗)−xi,j∗∣>τloss0, otherwise
注意这里的0,可以这样理解:设置0之后,就不用计算对应位置的 grad 了。
相关文章:

车道线检测-PolyLaneNet 论文学习笔记
论文:《PolyLaneNet: Lane Estimation via Deep Polynomial Regression》代码:https://github.com/lucastabelini/PolyLaneNet地址:https://arxiv.org/pdf/2004.10924.pdf参考:https://blog.csdn.net/sinat_17456165/article/deta…...
)
GO——接口(下)
接口接口值警告:一个包含空指针值的接口不是nil接口sort.Interface接口http.Handler接口类型断言类型分支接口值 接口值,由两个部分组成,一个具体的类型和那个类型的值。它们被称为接口的动态类型和动态值。对于像Go语言这种静态类型的语言&…...
计算机网络之http02| HTTPS HTTP1.1的优化
post与get请求的区别 get 是获取资源,Post是向指定URI提交资源,相关信息放在body里 2.http有哪些优点 (1)简单 报文只有报文首部和报文主体,易于理解 (2)灵活易拓展 URI相应码、首部字段都没有…...

基于matlab使用神经网络清除海杂波
一、前言此示例演示如何使用深度学习工具箱™训练和评估卷积神经网络,以消除海上雷达 PPI 图像中的杂波返回。深度学习工具箱提供了一个框架,用于设计和实现具有算法、预训练模型和应用程序的深度神经网络。二、数据集该数据集包含 84 对合成雷达图像。每…...

每天10个前端小知识 【Day 8】
前端面试基础知识题 1. Javascript中如何实现函数缓存?函数缓存有哪些应用场景? 函数缓存,就是将函数运算过的结果进行缓存。本质上就是用空间(缓存存储)换时间(计算过程), 常用于…...
【项目精选】基于Java的敬老院管理系统的设计和实现
本系统主要是针对敬老院工作人员即管理员和员工设计的。敬老院管理系统 将IT技术为养老院提供一个接口便于管理信息,存储老人个人信息和其他信息,查找 和更新信息的养老院档案,节省了员工的劳动时间,大大降低了成本。 其主要功能包括: 系统管理员用户功能介绍&#…...
Spark SQL 介绍
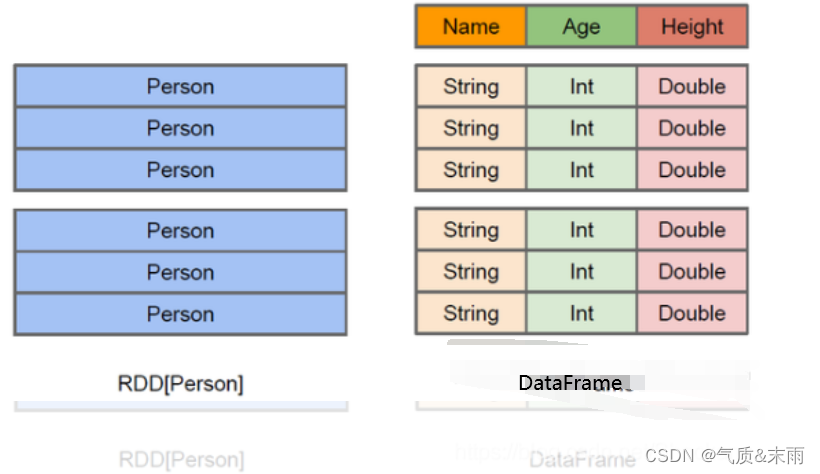
文章目录Spark SQL1、Hive on SparkSQL2、SparkSQL 优点3、SparkSQL 特点1) 容易整合2) 统一的数据访问3) 兼容 Hive4) 标准的数据连接4、DataFrame 是什么5、DataSet 是什么Spark SQL Spark SQL 是 Spark 用于结构化数据(structured data) 处理的Spark模块。 1、Hive on Spa…...

升级到 CDP 后Hive on Tez 性能调整和故障排除指南
优化Hive on Tez查询永远不能以一种万能的方法来完成。查询的性能取决于数据的大小、文件类型、查询设计和查询模式。在性能测试期间,要评估和验证配置参数和任何 SQL 修改。建议在工作负载的性能测试期间一次进行一项更改,并且最好在生产环境中使用它们…...

理解HDFS工作流程与机制,看这篇文章就够了
HDFS(The Hadoop Distributed File System) 是最初由Yahoo提出的分布式文件系统,它主要用来: 1)存储大数据 2)为应用提供大数据高速读取的能力 重点是掌握HDFS的文件读写流程,体会这种机制对整个分布式系统性能提升…...

Intel处理器分页机制
分页模式 Intel 64位处理器支持3种分页模式: 32-bit分页PAE分页IA-32e分页 32-bit分页 32-bit分页模式支持两种页面大小:4KB以及4MB。 4KB页面的线性地址转换 4MB页面的线性地址转换 PAE分页模式 PAE分页模式支持两种页面大小:4KB以及…...
Linux常用命令
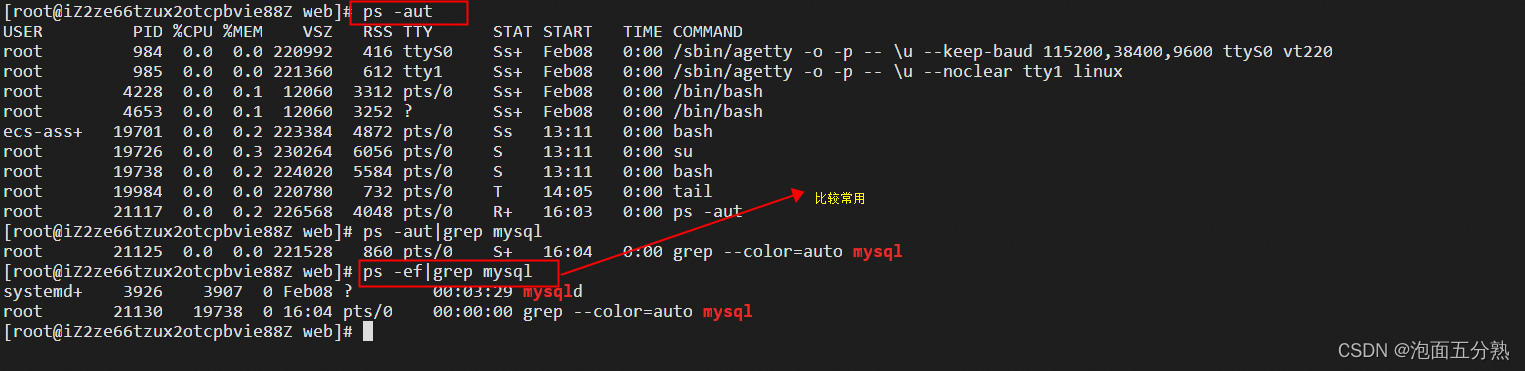
linux常用命令创建一个目录mkdir 命令可以创建新目录。mkdir 是 make directory 的缩写。[rootiZ2ze66tzux2otcpbvie88Z ~]# ls [rootiZ2ze66tzux2otcpbvie88Z ~]# mkdir web [rootiZ2ze66tzux2otcpbvie88Z ~]# ls web [rootiZ2ze66tzux2otcpbvie88Z ~]# 创建一个文件2.1 在 Li…...

基于STM32设计的音乐播放器
一、项目背景与设计思路 1.1 项目背景 时代进步,科学技术的不断创新,促进电子产品的不断更迭换代,各种新功能和新技术的电子产品牵引着消费者的眼球。人们生活水平的逐渐提高,对娱乐消费市场需求日益扩大,而其消费电子产品在市场中的占有份额越来越举足轻重。目前消费电…...

微服务开发
目录 微服务配置管理 权限认证 批处理 定时任务 异步 微服务调用 (协议)...
【(C语言)数据结构奋斗100天】二叉树(上)
【(C语言)数据结构奋斗100天】二叉树(上) 🏠个人主页:泡泡牛奶 🌵系列专栏:数据结构奋斗100天 本期所介绍的是二叉树,那么什么是二叉树呢?在知道答案之前,请大家思考一下…...
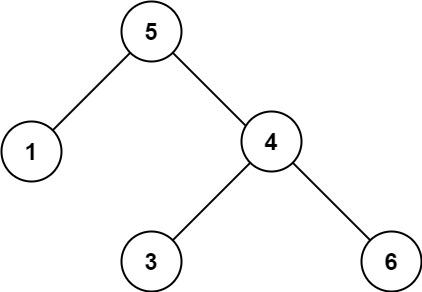
Java 验证二叉搜索树
验证二叉搜索树中等给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效 二叉搜索树定义如下:节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。示例 1&…...

C/C++单项选择题标准化考试系统[2023-02-09]
C/C单项选择题标准化考试系统[2023-02-09] ©3.17 单项选择题标准化考试系统 【难度系数】5级 【任务描述】 设计一个单项选择题的考试系统,可实现试题维护、自动组卷等功能。 【功能描述】 (1)管理员功能: 试题管理:每个试题包括题干、四个备选答案标准答案…...
爱了爱了,这些顶级的 Python 工具包太棒了
Python 语言向来以丰富的第三方库而闻名,今天来介绍几个非常nice的库,有趣好玩且强大!推荐好好学习。 文章目录技术交流数据采集AKShareTuShareGoPUPGeneralNewsExtractor爬虫playwright-pythonawesome-python-login-modelDecryptLoginScylla…...
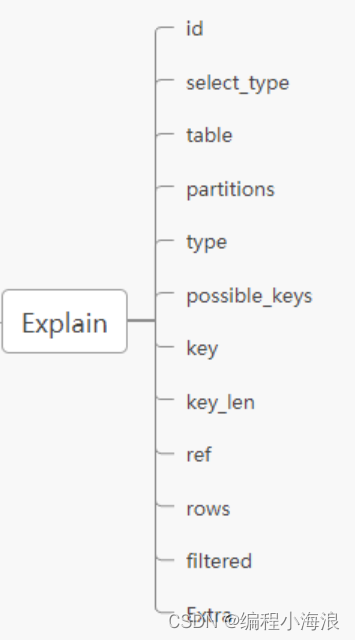
【Explain详解与索引优化最佳实践】
摘要 explain命令是查看MySQL查询优化器如何执行查询的主要方法,可以很好的分析SQL语句的执行情况。每当遇到执行慢(在业务角度)的SQL,都可以使用explain检查SQL的执行情况,并根据explain的结果相应的去调优SQL等。 …...
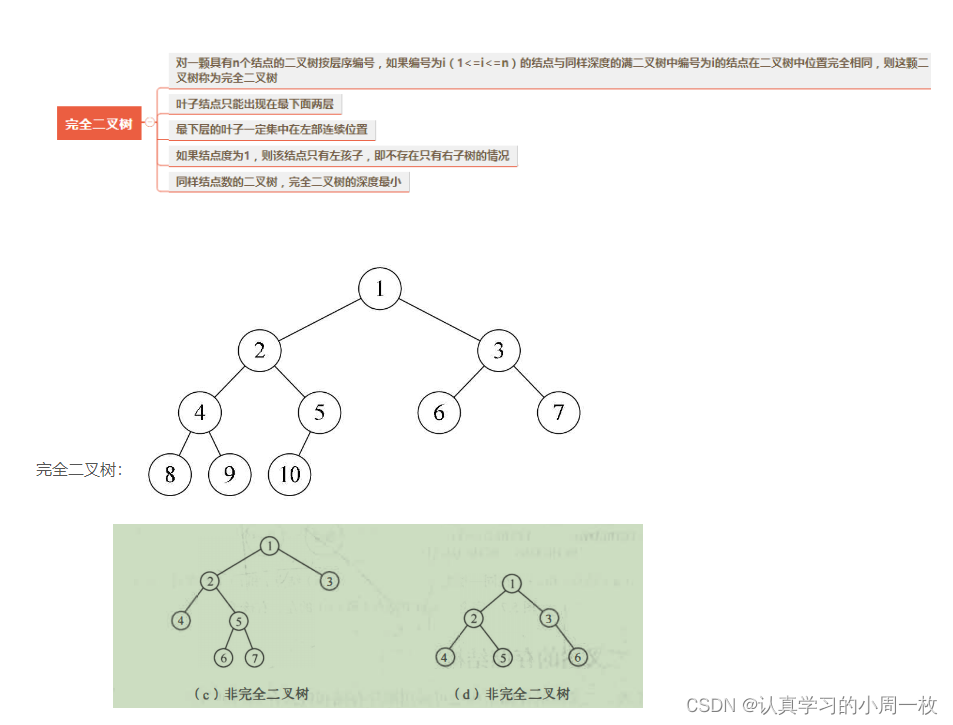
【树和二叉树】数据结构二叉树和树的概念认识
前言:在之前,我们已经把栈和队列的相关概念以及实现的方法进行了学习,今天我们将认识一个新的知识“树”!!! 目录1.树概念及结构1.1树的概念1.2树的结构1.3树的相关概念1.4 树的表示1.5 树在实际中的运用&a…...

通达信收费接口查询可申购新股c++源码分享
有很多股民在做股票交易时为了实现盈利会借助第三三方炒股工具帮助自己,那么通达信收费接口就是人们常用到的,今天小编来分享一下通达信收费接口查询可申购新股c源码: std::cout << " 查询可申购新股: category 12 \n"; c…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
