高等数学:线性代数-第二章
文章目录
- 第2章 矩阵及其运算
- 2.1 线性方程组和矩阵
- 2.2 矩阵的运算
- 2.3 逆矩阵
- 2.4 Cramer法则
第2章 矩阵及其运算
2.1 线性方程组和矩阵
n \bm{n} n 元线性方程组 设有 n 个未知数 m 个方程的线性方程组
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots + a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} = b_{2} \\ \cdots\cdots\cdots\cdots \\ a_{m1}x_{1} + a_{m2}x_{2} + \cdots + a_{mn}x_{n} = b_{m} \\ \end{cases} \\ ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯am1x1+am2x2+⋯+amnxn=bm
当常数项 b i b_{i} bi 不全为零时,称该方程组为n 元非齐次线性方程组,当 b i b_{i} bi 全为零时,称该方程组为n 元齐次线性方程组。
矩阵 由 m × n m \times n m×n 个数 a i j a_{ij} aij 排成的 m 行 n 列的数表
a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{matrix} \\ a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
称为 m × n m \times n m×n矩阵,记作
A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) \bm{A} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \\ A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
特别地,当 m = n 时,该矩阵叫做n 阶方阵。
增广矩阵 对于非齐次线性方程组
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ ⋯ ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots + a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} = b_{2} \\ \cdots\cdots\cdots\cdots \\ a_{m1}x_{1} + a_{m2}x_{2} + \cdots + a_{mn}x_{n} = b_{m} \\ \end{cases} \\ ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯am1x1+am2x2+⋯+amnxn=bm
它的系数矩阵、未知数矩阵和常数项矩阵分别如下:
A = ( a i j ) m × n x = ( x 1 x 2 ⋯ x n ) b = ( b 1 b 2 ⋯ b m ) \begin{align} &\bm{A} = (a_{ij})_{m \times n} \\ &\bm{x} = \begin{pmatrix} x_{1} & x_{2} & \cdots & x_{n} \\ \end{pmatrix} \\ &\bm{b} = \begin{pmatrix} b_{1} & b_{2} & \cdots & b_{m} \\ \end{pmatrix} \\ \end{align} \\ A=(aij)m×nx=(x1x2⋯xn)b=(b1b2⋯bm)
它的增广矩阵定义为
B = ( A b ) = ( a 11 a 12 ⋯ a 1 n b 1 a 21 a 22 ⋯ a 2 n b 2 ⋮ ⋮ ⋱ ⋮ ⋮ a m 1 a m 2 ⋯ a m n b m ) \bm{B} = ( \begin{array}{c|c} \bm{A} & \bm{b} \end{array} ) = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_{1} \\ a_{21} & a_{22} & \cdots & a_{2n} & b_{2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_{m} \\ \end{pmatrix} \\ B=(Ab)= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amnb1b2⋮bm
对角矩阵 方阵
( λ 1 λ 2 ⋱ λ n ) \begin{pmatrix} \lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n} \\ \end{pmatrix} \\ λ1λ2⋱λn
叫做对角矩阵,简称对角阵,记作 d i a g ( λ 1 λ 2 ⋯ λ n ) \mathrm{diag}(\begin{array}{ccc} \lambda_{1} & \lambda_{2} & \cdots & \lambda_{n} \end{array}) diag(λ1λ2⋯λn) .
单位矩阵 对角矩阵 d i a g ( 1 1 ⋯ 1 ) \mathrm{diag}(\begin{array}{ccc} 1 & 1 & \cdots & 1 \end{array}) diag(11⋯1) 叫做 n 阶单位矩阵,简称单位阵,记作 E n \bm{E}_{n} En .
2.2 矩阵的运算
矩阵加法
A + B = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) + ( b 11 b 12 ⋯ b 1 n b 21 b 22 ⋯ b 2 n ⋮ ⋮ ⋱ ⋮ b m 1 b m 2 ⋯ b m n ) = ( a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 + b 21 a 22 + b 22 ⋯ a 2 n + b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 + b m 1 a m 2 + b m 2 ⋯ a m n + b m n ) \begin{align} \bm{A} + \bm{B} &= \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \\ \end{pmatrix} \\ &= \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\ a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn} \\ \end{pmatrix} \\ \end{align} \\ A+B= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn + b11b21⋮bm1b12b22⋮bm2⋯⋯⋱⋯b1nb2n⋮bmn = a11+b11a21+b21⋮am1+bm1a12+b12a22+b22⋮am2+bm2⋯⋯⋱⋯a1n+b1na2n+b2n⋮amn+bmn
矩阵加法满足:
A + B = B + A ( A + B ) + C = A + ( B + C ) \bm{A} + \bm{B} = \bm{B} + \bm{A} (\bm{A} + \bm{B}) + \bm{C} = \bm{A} + (\bm{B} + \bm{C}) A+B=B+A(A+B)+C=A+(B+C)
矩阵数乘
c A = c ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ) = ( c a 11 c a 12 ⋯ c a 1 n c a 21 c a 22 ⋯ c a 2 n ⋮ ⋮ ⋱ ⋮ c a m 1 c a m 2 ⋯ c a m n ) \begin{align} c\bm{A} &= c \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \\ &= \begin{pmatrix} ca_{11} & ca_{12} & \cdots & ca_{1n} \\ ca_{21} & ca_{22} & \cdots & ca_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ ca_{m1} & ca_{m2} & \cdots & ca_{mn} \\ \end{pmatrix} \\ \end{align} \\ cA=c a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn = ca11ca21⋮cam1ca12ca22⋮cam2⋯⋯⋱⋯ca1nca2n⋮camn
矩阵数乘满足:
c A = A c ( λ μ ) A = λ ( μ A ) ( λ + μ ) A = λ A + μ A λ ( A + B ) = λ A + λ B c\bm{A} = \bm{A}c (\lambda\mu)\bm{A} = \lambda(\mu\bm{A}) (\lambda + \mu)\bm{A} = \lambda\bm{A} + \mu\bm{A} \lambda(\bm{A} + \bm{B})=\lambda\bm{A} + \lambda\bm{B} cA=Ac(λμ)A=λ(μA)(λ+μ)A=λA+μAλ(A+B)=λA+λB
矩阵乘法 对于 m × s m \times s m×s矩阵 A \bm{A} A 和 s × n s \times n s×n矩阵 B \bm{B} B ,它们的乘法定义为 C = A B = ( c i j ) m × n \bm{C} = \bm{A}\bm{B} = (c_{ij})_{m \times n} C=AB=(cij)m×n ,且满足
c i j = ∑ k = 1 s a i k b k j ( i ∈ Z ≤ m , j ∈ Z ≤ n ) c_{ij} = \sum_{k = 1}^{s}a_{ik}b_{kj} ~~~~ (i \in \mathbb{Z} \leq m, j \in \mathbb{Z} \leq n) \\ cij=k=1∑saikbkj (i∈Z≤m,j∈Z≤n)
矩阵乘法满足:
( A B ) C = A ( B C ) c ( A B ) = ( c A ) B = A ( c B ) A ( B + C ) = A B + A C ( B + C ) A = B A + C A (\bm{A}\bm{B})\bm{C} = \bm{A}(\bm{B}\bm{C}) c(\bm{A}\bm{B}) = (c\bm{A})\bm{B} = \bm{A}(c\bm{B}) \bm{A}(\bm{B} + \bm{C}) = \bm{A}\bm{B} + \bm{A}\bm{C} (\bm{B} + \bm{C})\bm{A} = \bm{B}\bm{A} + \bm{C}\bm{A} (AB)C=A(BC)c(AB)=(cA)B=A(cB)A(B+C)=AB+AC(B+C)A=BA+CA
需要注意的是,
A B ≠ B A ( B ≠ E ) . \bm{A}\bm{B} \ne \bm{B}\bm{A} ~~~~ (\bm{B} \ne \bm{E}) . AB=BA (B=E).
矩阵转置 矩阵 A = ( a i j ) m × n \bm{A} = (a_{ij})_{m \times n} A=(aij)m×n的转置矩阵记作 A T \bm{A}^\mathrm{T} AT ,且满足
A T = ( a j i ) n × m \bm{A}^\mathrm{T} = (a_{ji})_{n \times m} \\ AT=(aji)n×m
矩阵转置满足:
( A T ) T = A ( A + B ) T = A T + B T ( λ A ) T = λ A T ( A B ) T = B T A T (\bm{A}^{T})^{T} = \bm{A} (\bm{A} + \bm{B})^\mathrm{T} = \bm{A}^\mathrm{T} + \bm{B}^\mathrm{T} (\lambda \bm{A})^\mathrm{T} = \lambda\bm{A}^\mathrm{T} (\bm{A}\bm{B})^\mathrm{T} =\bm{B}^\mathrm{T}\bm{A}^\mathrm{T} (AT)T=A(A+B)T=AT+BT(λA)T=λAT(AB)T=BTAT
方阵的行列式 由 n 阶方阵 A \bm{A} A的元素所构成的行列式,称为方阵 A \pmb{A} A 的行列式,记作 det A \det\bm{A} detA或 ∣ A ∣ | \bm{A} | ∣A∣
方阵的行列式满足:
∣ A T ∣ = ∣ A ∣ ∣ λ A ∣ = λ n ∣ A ∣ | \bm{A}^\mathrm{T} | = | \bm{A} | | \lambda\bm{A} | = \lambda^{n} | \bm{A} | ∣AT∣=∣A∣∣λA∣=λn∣A∣
其中 n 为矩阵 A \bm{A} A的阶数
∣ A B ∣ = ∣ A ∣ ∣ B ∣ | \pmb{A}\bm{B} | = | \pmb{A} || \bm{B} | ∣AB∣=∣A∣∣B∣
2.3 逆矩阵
伴随矩阵 行列式 | \bm{A} | 的各个元素的代数余子式 A_{ij} 所构成的如下的矩阵
A ∗ = ( A 11 A 21 ⋯ A n 1 A 12 A 22 ⋯ A n 2 ⋮ ⋮ ⋱ ⋮ A 1 n A 2 n ⋯ A n n ) \bm{A}^{*} = \begin{pmatrix} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \\ \end{pmatrix} \\ A∗= A11A12⋮A1nA21A22⋮A2n⋯⋯⋱⋯An1An2⋮Ann
称为矩阵 A \bm{A} A的伴随矩阵,简称伴随阵,记作 A ∗ \bm{A}^{*} A∗
矩阵 A \bm{A} A和它的伴随矩阵 A ∗ \bm{A}^{*} A∗ 满足
A A ∗ = A ∗ A = ∣ A ∣ E \bm{A}\bm{A}^{*}=\bm{A}^{*}\bm{A}=|\bm{A}|\bm{E} \\ AA∗=A∗A=∣A∣E
逆矩阵 对于 n 阶矩阵 A \bm{A} A,如果有一个 n 阶矩阵 B \bm{B} B ,使得
A B = B A = E \bm{A}\bm{B} = \bm{B}\bm{A} = \bm{E} \\ AB=BA=E
则说矩阵 A \bm{A} A是可逆的,并把矩阵 B \bm{B} B称为矩阵 A \bm{A} A的逆矩阵,简称逆阵,记作 A − 1 \bm{A}^{-1} A−1.
如果矩阵 A \bm{A} A是可逆的,那么 A \bm{A} A 的逆矩阵是惟一的。
矩阵 A \bm{A} A 可逆的充分必要条件是 ∣ A ∣ ≠ 0 | \bm{A} | \ne 0 ∣A∣=0 。若 ∣ A ∣ ≠ 0 | \bm{A} | \ne 0 ∣A∣=0,则
A − 1 = 1 ∣ A ∣ A ∗ \bm{A}^{-1} = \frac{1}{| \bm{A} |}\bm{A}^{*} \\ A−1=∣A∣1A∗
逆矩阵满足:
( A − 1 ) − 1 = A ( λ A ) − 1 = λ − 1 A − 1 (\bm{A}^{-1})^{-1} = \bm{A} (\lambda \bm{A})^{-1} = \lambda^{-1}\bm{A}^{-1} (A−1)−1=A(λA)−1=λ−1A−1
若 A \bm{A} A、 B \bm{B} B 为同阶矩阵且均可逆,则
( A B ) − 1 = B − 1 A − 1 (\bm{A}\bm{B})^{-1} = \bm{B}^{-1}\bm{A}^{-1} (AB)−1=B−1A−1
奇异矩阵 不可逆矩阵叫做奇异矩阵。
非奇异矩阵 可逆矩阵叫做非奇异矩阵。
2.4 Cramer法则
Cramer法则 如果线性方程组
{ a 11 x 1 + a 12 x 2 + ⋯ = b 1 a 21 x 1 + a 22 x 2 + ⋯ = b 2 ⋯ ⋯ ⋯ ⋯ a n 1 x 1 + a n 2 x 2 + ⋯ = b n \begin{cases} a_{11}x_{1} + a_{12}x_{2} + \cdots = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} + \cdots = b_{2} \\ \cdots\cdots\cdots\cdots \\ a_{n1}x_{1} + a_{n2}x_{2} + \cdots = b_{n} \\ \end{cases} \\ ⎩ ⎨ ⎧a11x1+a12x2+⋯=b1a21x1+a22x2+⋯=b2⋯⋯⋯⋯an1x1+an2x2+⋯=bn
的系数矩阵 A 的行列式不等于零,即
∣ A ∣ = ∣ a 11 ⋯ a 1 n ⋮ ⋮ a n 1 ⋯ a n n ∣ ≠ 0 \left\lvert A \right\rvert = \begin{vmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \\ \end{vmatrix} \ne 0 \\ ∣A∣= a11⋮an1⋯⋯a1n⋮ann =0
则该方程组有惟一解
x i = ∣ A i ∣ ∣ A ∣ x_{i} = \frac{\left\lvert A_{i} \right\rvert}{\left\lvert A \right\rvert} \\ xi=∣A∣∣Ai∣
其中
A i = ( a 11 ⋯ a 1 , i − 1 b 1 a 1 , i + 1 ⋯ a 1 n ⋮ ⋮ ⋮ ⋮ ⋮ a n 1 ⋯ a n , i − 1 b n a n , i + 1 ⋯ a n n ) A_{i} = \begin{pmatrix} a_{11} & \cdots & a_{1, i - 1} & b_{1} & a_{1, i + 1} & \cdots & a_{1n} \\ \vdots & & \vdots & \vdots & \vdots & & \vdots \\ a_{n1} & \cdots & a_{n, i - 1} & b_{n} & a_{n, i + 1} & \cdots & a_{nn} \\ \end{pmatrix} \\ Ai= a11⋮an1⋯⋯a1,i−1⋮an,i−1b1⋮bna1,i+1⋮an,i+1⋯⋯a1n⋮ann
相关文章:

高等数学:线性代数-第二章
文章目录 第2章 矩阵及其运算2.1 线性方程组和矩阵2.2 矩阵的运算2.3 逆矩阵2.4 Cramer法则 第2章 矩阵及其运算 2.1 线性方程组和矩阵 n \bm{n} n 元线性方程组 设有 n 个未知数 m 个方程的线性方程组 { a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 a 21 x 1 a 22 x 2 ⋯ a …...

星戈瑞分析FITC-PEG-Alkyne的荧光特性和光谱特性
欢迎来到星戈瑞荧光stargraydye!小编带您盘点: FITC-PEG-Alkyne的荧光特性和光谱特性是对其荧光性能进行分析的方面。以下是FITC-PEG-Alkyne的一些常见荧光特性和光谱特性: **1. 荧光激发波长:**FITC-PEG-Alkyne的荧光激发波长通…...

VB.NET调用VB6 Activex EXE实现PowerBasic和FreeBasic的标准DLL调用
VB6写的ActiveX EXE公共对象是外置进程,因此,尽管它是x86 32位的进程,但可以集成到 VB.NET的x64和x32程序中使用。 VS2022的VB.NET程序,调用ActiveX DLL对象我在上篇笔记中写了 VB.NET通过VB6 ActiveX DLL调用PowerBasic及FreeB…...
(下篇))
深入了解Unity的Physics类:一份详细的技术指南(七)(下篇)
接着上一篇深入了解Unity的Physics类(上篇),我们继续把Physics类剩余的属性和方法进行讲解 碰撞检测和忽略: (这些方法和属性涉及查询和处理物体之间的碰撞) Physics.CheckBox: 检查给定位置的盒子是否与任何碰撞器接触或者位于任何碰撞器内部。 Physics.CheckCapsu…...
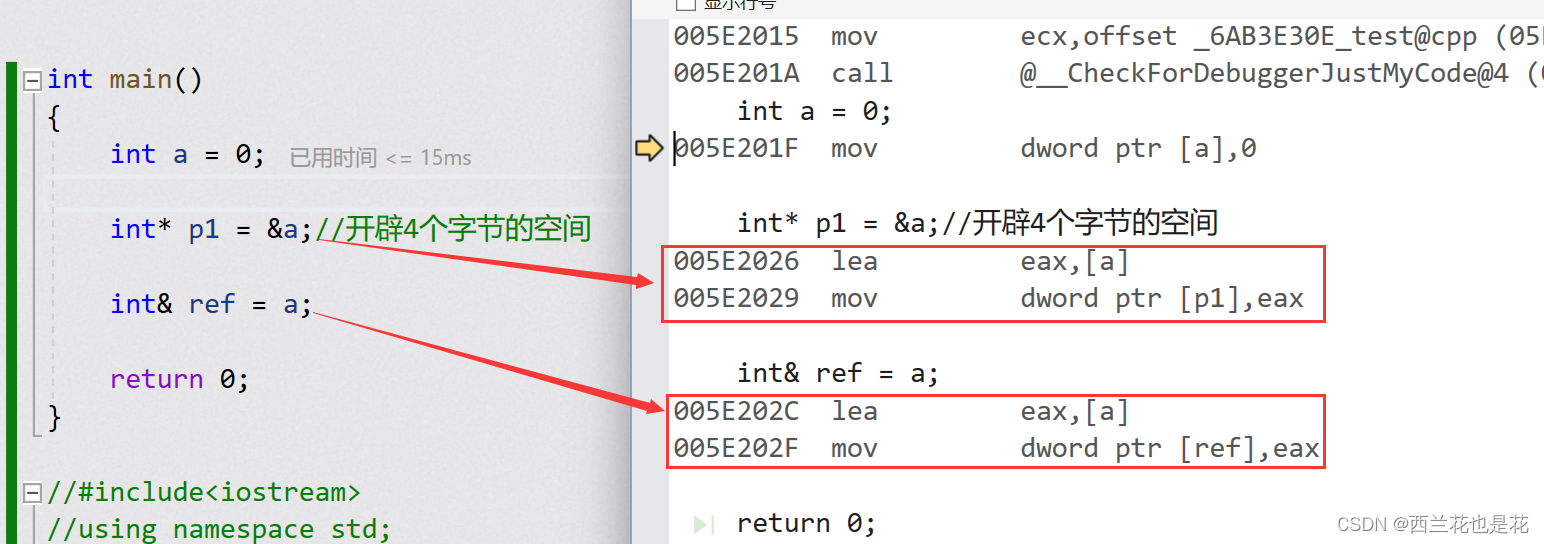
C++入门:引用是什么
目录 1.引用的概念 2.引用的特征 3.常引用 4.引用使用场景 5.传值,传引用效率比较 6.引用与指针的区别 1.引用的概念 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空 间,它和它引用…...

2023年人工智能与自动化控制国际学术会议(AIAC 2023)
2023年人工智能与自动化控制国际学术会议(AIAC 2023) The 2023 International Conference on Artificial Intelligence and Automation Control 2023年人工智能与自动化控制国际学术会议(AIAC 2023)将于2023年10月27-29日在中…...
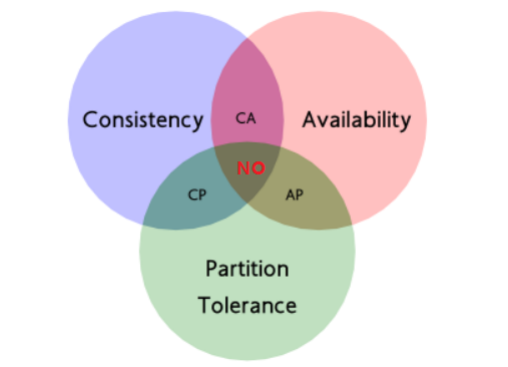
分布式核心知识以及常见微服务框架
分布式中的远程调用 在微服务架构中,通常存在多个服务之间的远程调用的需求。远程调用通常包含两个部分:序列化和通信协议。常见的序列化协议包括json、xml、 hession、 protobuf、thrift、text、 bytes等,目前主流的远程调用技术有基于HTTP…...

Unity记录4.1-存储-根据关键字加载Tile
文章首发见博客:https://mwhls.top/4810.html。 无图/格式错误/后续更新请见首发页。 更多更新请到mwhls.top查看 欢迎留言提问或批评建议,私信不回。 汇总:Unity 记录 摘要:实现完 Tilemap 地图生成后,实现根据关键字…...
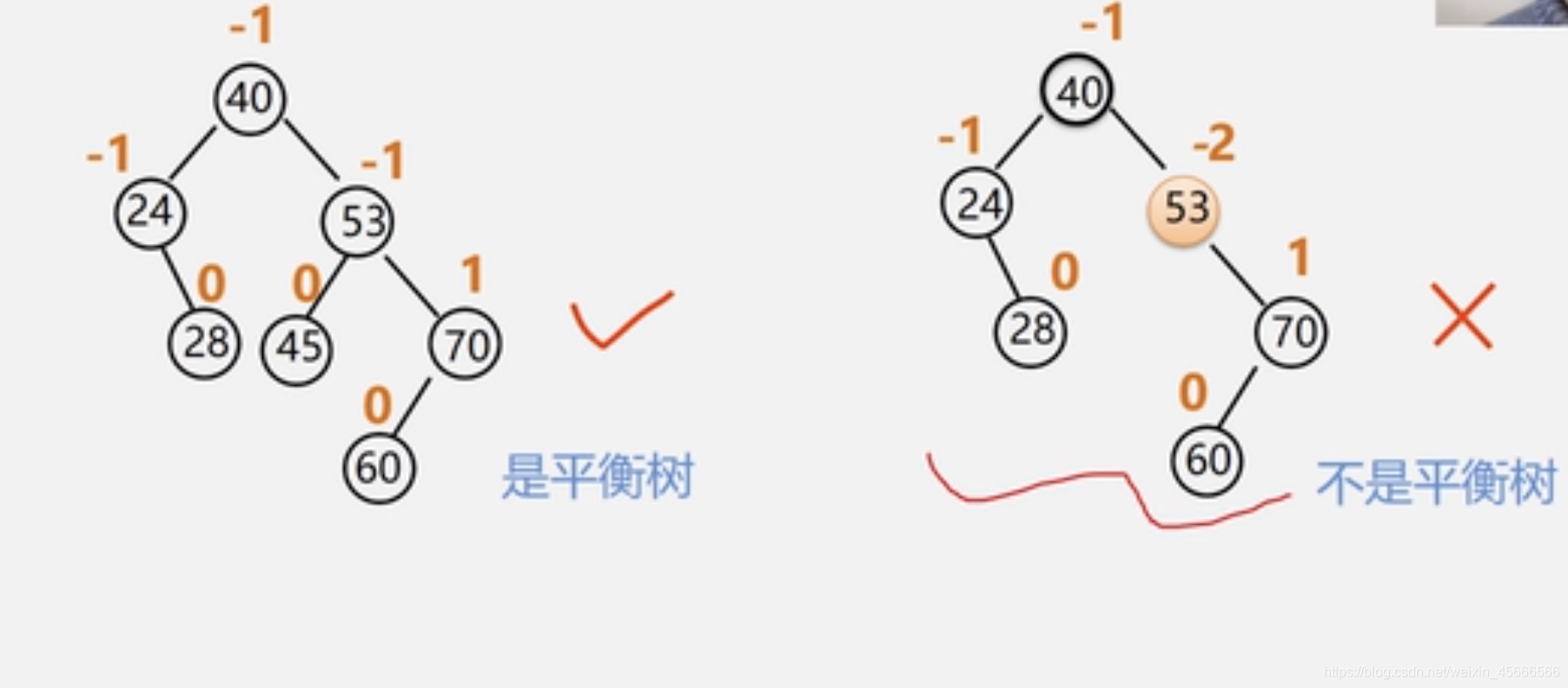
数据结构—树表的查找
7.3树表的查找 当表插入、删除操作频繁时,为维护表的有序表,需要移动表中很多记录。 改用动态查找表——几种特殊的树 表结构在查找过程中动态生成 对于给定值key 若表中存在,则成功返回; 否则࿰…...

微信小程序测试策略和注意事项?
一、测试前准备(环境搭建) 1、前端页面 微信 Web 开发者工具安装、授权测试用的微信号可预览和调试小程序 2、管理后台 配置内网测试服务器环境,通过 PC 端 Web 站点管理小程序前端的输出内容,可从开发人员获取管理账号进行测…...

VUE3封装EL-ELEMENT-PLUS input组件
VUE3封装EL-ELEMENT-PLUS input组件 完整代码 <template><div><div><div class"lable_top" v-if"label"><label :class"lable_sty">{{ label }}</label></div><el-inputv-model"inputValue&…...

RISC-V公测平台发布 · 在SG2042上配置Jupiter+Octave科学计算环境
简介 JupyterHub是一个开源的共享计算平台,它为每个用户管理一个单独的 Jupyter 环境, 可以用于学生班级、企业数据科学小组或科学研究小组。它是一个多用户中心,可以生成、管理和代理多个单用户Jupyter笔记本服务器的实例。 GNU Octave是一…...
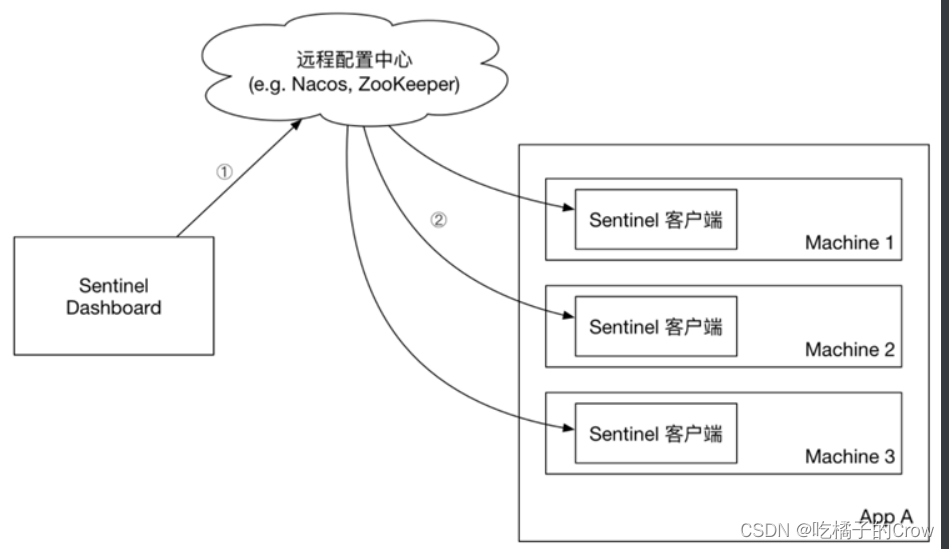
初识Sentinel
目录 1.解决雪崩的方式有4种: 1.1.2超时处理: 1.1.3仓壁模式 1.1.4.断路器 1.1.5.限流 1.1.6.总结 1.2.服务保护技术对比 1.3.Sentinel介绍和安装 1.3.1.初识Sentinel 1.3.2.安装Sentinel 1.4.微服务整合Sentinel 2.流量控制 2.1.簇点链路 …...

【官方中文文档】Mybatis-Spring #注入映射器
注入映射器 与其在数据访问对象(DAO)中手工编写使用 SqlSessionDaoSupport 或 SqlSessionTemplate 的代码,还不如让 Mybatis-Spring 为你创建一个线程安全的映射器,这样你就可以直接注入到其它的 bean 中了: <bea…...
UG\NX 二次开发 相切面、相邻面的选择控件
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan 简介: 有群友问“UFUN多选功能过滤面不能选择相切面或相邻面之类的吗?” 这个用Block UI的"面收集器"就可以,ufun函数是不行的。 效果: C++语言在UG二次开发中的应用及综合分析 C++ …...
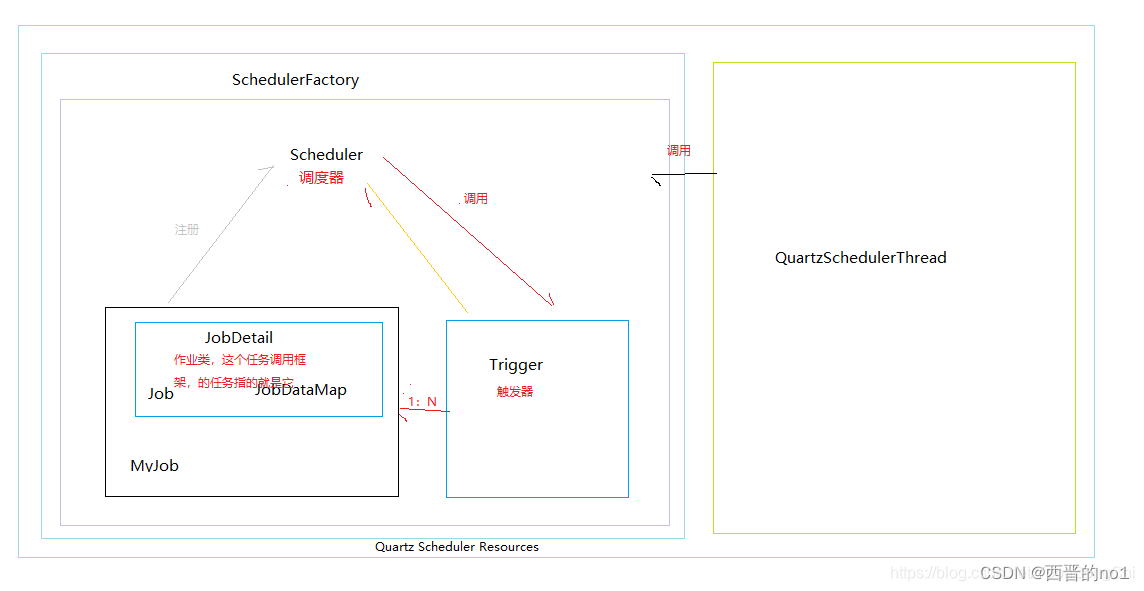
Quartz任务调度框架介绍和使用
一、Quartz介绍 Quartz [kwɔːts] 是OpenSymphony开源组织在Job scheduling领域又一个开源项目,完全由Java开发,可以用来执行定时任务,类似于java.util.Timer。但是相较于Timer, Quartz增加了很多功能: 1.持久性作业 …...
drools8尝试
drools7升级到drools8有很大很大的变更.几乎不能说是一个项目了. 或者说就是名字相同的不同项目, 初看下来变化是这样 两个最关键的东西都retired了 https://docs.drools.org/8.42.0.Final/drools-docs/drools/migration-guide/index.html business central变成了一个VS code…...
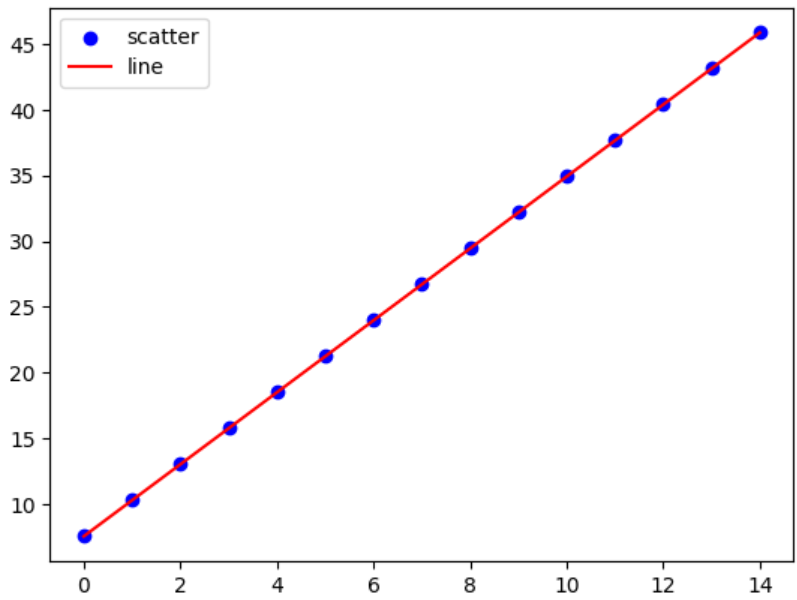
【机器学习】python基础实现线性回归
手写梯度下降的实现ykxb的线性回归 算法步骤: (1)构造数据,y3*x5; (2)随机初始化和,任意数值,例如9,10; (3)计算,,并计算 (4&…...
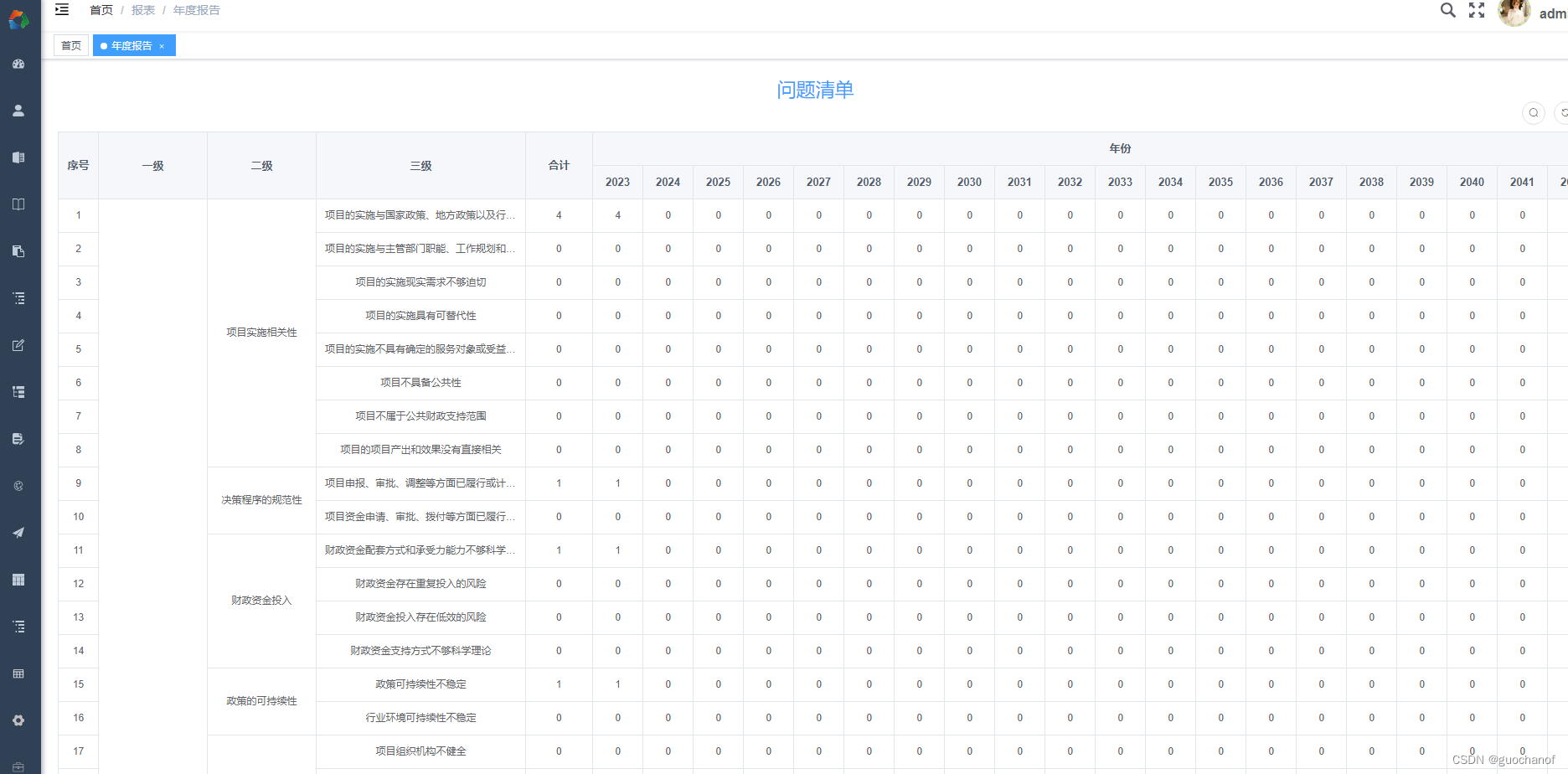
vue table合并行 动态列名
需求: 1.合并行,相同数据合并 2,根据后端返回数据动态显示列名, 我这个业务需求是,每年增加一列,也就是列名不是固定的,后端返回数据每年会多一条数据,根据返回数据显示列名 实现: html <el-table v-loading"loading" :data"dataList" :span-metho…...
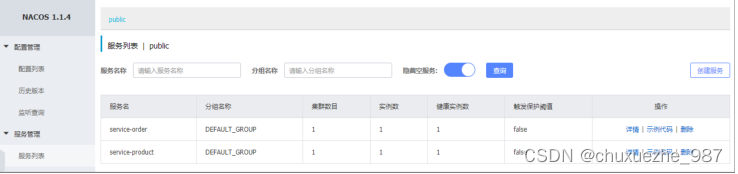
Spring Cloud Alibaba-Nacos Discovery--服务治理
1 服务治理介绍 先来思考一个问题 通过上一章的操作,我们已经可以实现微服务之间的调用。但是我们把服务提供者的网络地址 (ip,端口)等硬编码到了代码中,这种做法存在许多问题: 一旦服务提供者地址变化&am…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
