go生成文件md5、sha1摘要简单示例
备注
go官方文档 https://pkg.go.dev/crypto/md5 已经给出如何使用该package生成文件或者字节数组的摘要值, 参照即可。 摘要值不是对文内容的加密,它主要用来进行checksum,就是验证两个文件内容是否一致,是否被篡改或者变化了。
简介
“crypto/sha256”
“crypto/md5”
“crypto/sha1”
根据文档介绍, 可直接通过如下方式对字节数据或者文件流进行摘要获取
对字节数据获取摘要
s := "Foo"md5 := md5.Sum([]byte(s))
sha1 := sha1.Sum([]byte(s))
sha256 := sha256.Sum256([]byte(s))fmt.Printf("%x\n", md5)
fmt.Printf("%x\n", sha1)
fmt.Printf("%x\n", sha256)
对文件取摘要值示例。 将如下示例代码中的sha256.New() 替换为h := sha1.New(), 即可获取sha1值, 通过fmt.Printf(“%x\n”, sum)获取摘要值的字符串, 也可以通过hex.EncodeToString(md5Byte) 将摘要值encode为可以打印的字符串。
func main() {f, err := os.Open("file.txt")if err != nil {log.Fatal(err)}defer f.Close()h := sha256.New()if _, err := io.Copy(h, f); err != nil {log.Fatal(err)}fmt.Printf("%x", h.Sum(nil))
}
示例代码
package mainimport ("crypto/md5""encoding/hex""fmt""io""os"
)func calcFileMD5(filePath string) (string, error) {file, err := os.Open(filePath)if err != nil {return "", err}md5Handle := md5.New()_, _ = io.Copy(md5Handle, file)md5Byte := md5Handle.Sum(nil) //计算 MD5 值,返回 []bytemd5str := fmt.Sprintf("%x", md5Byte) //将 []byte 转为 stringfmt.Printf("md5Byte:%v, md5str:%v\n", md5Byte, md5str)return hex.EncodeToString(md5Byte), nil
}func main() {dir, err := os.Getwd()if err != nil {fmt.Println("Error getting current directory: ", err)return}fmt.Println("Current dir: ", dir)var fileName = "file1.txt"md5Val, err := calcFileMD5(fileName)if err != nil {fmt.Printf("fail to calc md5 for file %v, errMsg:%v\n", fileName, err)} else {fmt.Printf("md5 for file %v is %v\n", fileName, md5Val)}fmt.Println("字符串的md5值demo")str := "要取摘要的字符串abc"md5Handle := md5.New()_, err = io.WriteString(md5Handle, str)if err != nil {fmt.Printf("fail to calc md5 for string %v is errMsg:%v\n", str, err)return}md5ValByte := md5Handle.Sum(nil)// 输出16进制格式的MD5字符串fmt.Printf("%x\n", md5ValByte)md5str := hex.EncodeToString(md5ValByte)fmt.Printf("md5 for string %v is %v. lenght:%d\n", str, md5str, len(md5ValByte))fmt.Println("byte 数组的md5值demo")dataByte := []byte("要取摘要的数据") // 将字符串转换为byte数组md5Val16Byte := md5.Sum(dataByte) // 对data进行MD5哈希计算// 输出16进制格式的MD5字符串fmt.Printf("%x\n", md5Val16Byte)sliceFrom16ByteArray := md5Val16Byte[:]md5str = hex.EncodeToString(sliceFrom16ByteArray)fmt.Printf("md5 for byte[] %v is %v. lenght:%d\n", dataByte, md5str, len(md5Val16Byte))
}相关文章:

go生成文件md5、sha1摘要简单示例
备注 go官方文档 https://pkg.go.dev/crypto/md5 已经给出如何使用该package生成文件或者字节数组的摘要值, 参照即可。 摘要值不是对文内容的加密,它主要用来进行checksum,就是验证两个文件内容是否一致,是否被篡改或者变化了。…...
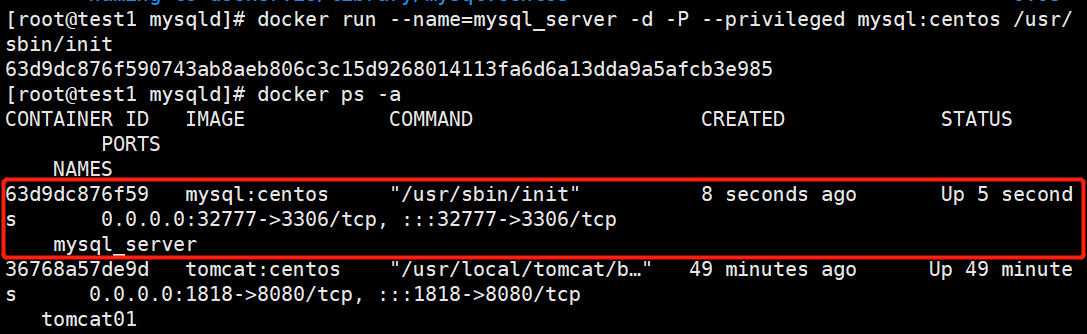
Docker容器:docker数据管理、镜像的创建及dockerfile案例
文章目录 一、docker数据管理1.为何需要docker数据管理2.数据管理类型3.数据卷4.数据卷容器5.容器的互联 二.docker镜像的三种创建方法1.基于现有镜像创建1.1 启动镜像1.2 生成新镜像 2.基于本地模板创建2.1 OPENVZ 下载模板2.2 导入容器生成镜像 3.基于dockerfile创建3.1 dock…...

Ajax fetch Axios 的区别
AJAX:一种创建交互式网页应用的网页执行交互技术 通过在后台与服务器进行少量数据交换,Ajax可以使网页实现异步更新。意味着:在不重新加载整个网页 的情况下,对网页某部分进行更新。 缺点: 针对MVC编程,…...
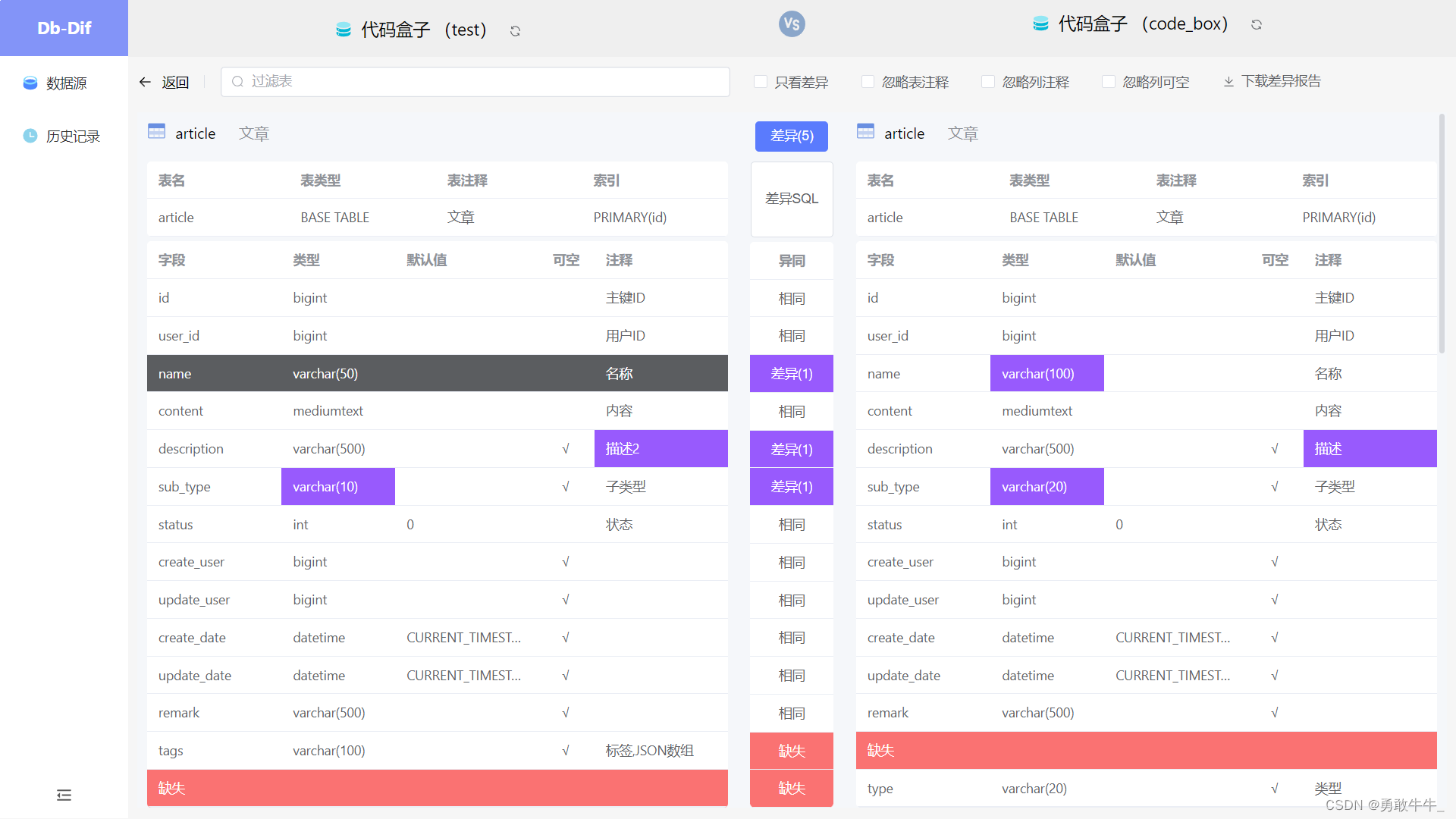
数据库结构差异对比工具
简介 前几年写了一个数据库对比工具,但是由于实现方式的原因,数据库支持有限,所以重新设计了一下,便于支持多种数据库,并且更新了UI。 新版地址:https://gitee.com/xgpxg/db-diff 旧版地址:h…...

Shell编程学习之breakcontinuereturn的应用
Shell编程中的break关键字:break关键字:退出最近的循环,后续循环不再执行;break关键字用法: break #结束本层循环 break 数字n #结束n层循环测试代码1: #!/bin/bashfor((i1;i<6;i)) dofor((…...
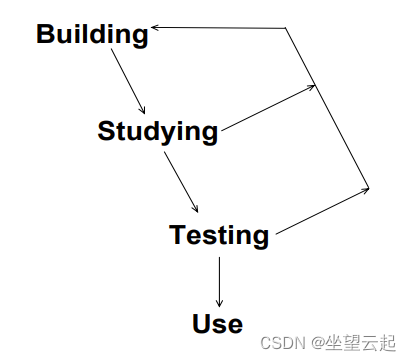
有趣的数学 数学建模入门二 一些理论基础
一、什么是数学建模? 现实世界中混乱的问题可以用数学来解决,从而产生一系列可能的解决方案来帮助指导决策。大多数人对数学建模的概念感到不舒服,因为它是如此开放。如此多的未知信息似乎令人望而却步。哪些因素最相关?但正是现实世界问题的…...
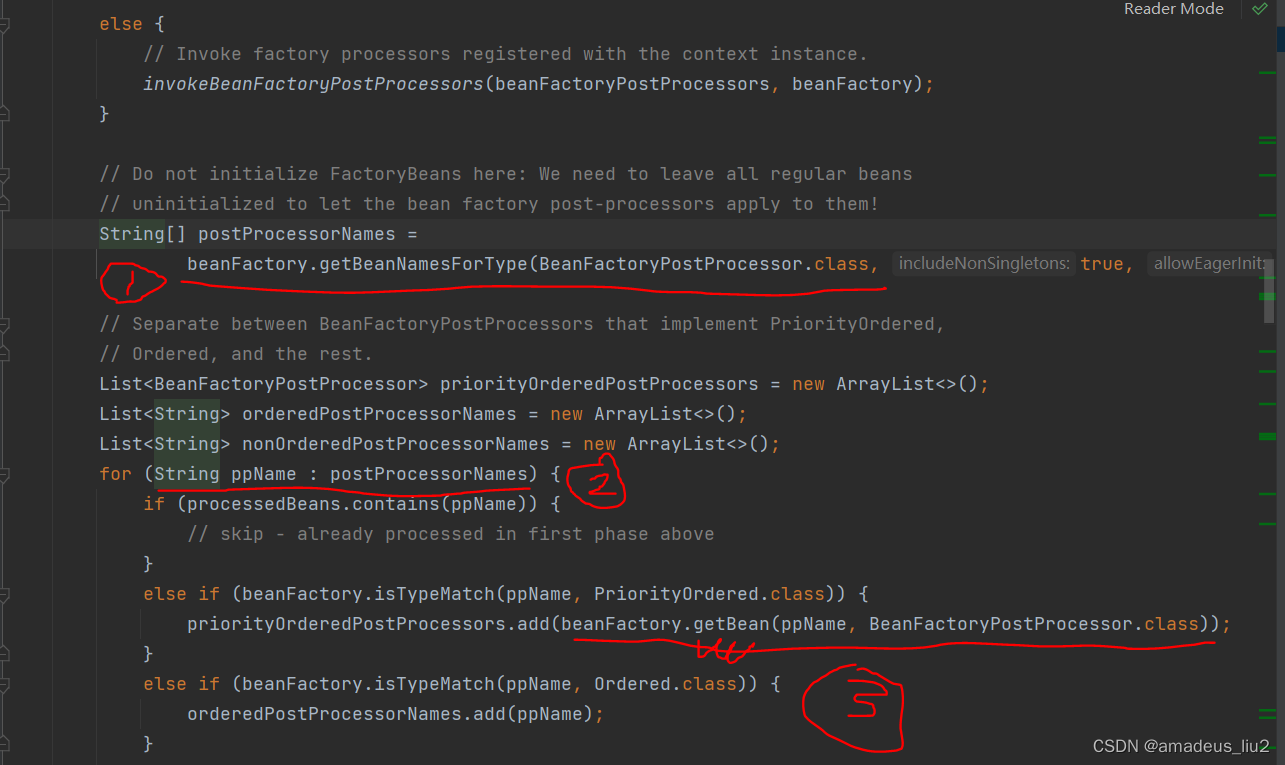
Spring复习:(55)ApplicationContext中BeanFactoryPostProcessor是怎么添加到容器的?
容器创建时会调用AbstractApplicationContext的refresh方法,其中会调用invokeBeanFactoryPostProcessor方法,如下图 invokeBeanFactoryPostProcessors代码如下: 其中调用的PostProcessorRegistrationDelegate的invokeBeanFactoryPostProcess…...

给wordpress添加关键词与描述
Wordpress网站的关键字及网页描述关系网站对搜索引擎的友好程度,如果自己手动加显然太折腾了,那如何让WordPress博客自动为每篇文章自动关键字及网页描述。每篇文章的内容不同,我们该如何让wordpress自动添加文章描述和关键词呢?下…...
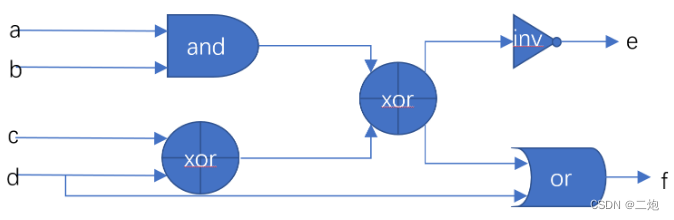
Verilog 入门
Verilog 入门 本内容来自 牛客网Verilog入门特别版 1、一个没有输入和一个输出常数1的输出的电路,输出信号为one module top_module(one);output wire one;assign one 1b1; endmodule2、创建一个具有一个输入和一个输出的模块,其行为类似于电路上的连…...

shell 简单且常用的几种
目录 一、配置环境的shell脚本 二、系统资源脚本 一、要求 二、脚本内容 三、脚本解析 四、赋权并验证 三、查看当前内存的总大小、实际使用大小、剩余大小、显示使用率百分比的脚本 一、第一种方法 二、验证 三、第二种方法 四、验证 四、查看网卡实时流量脚本 一…...
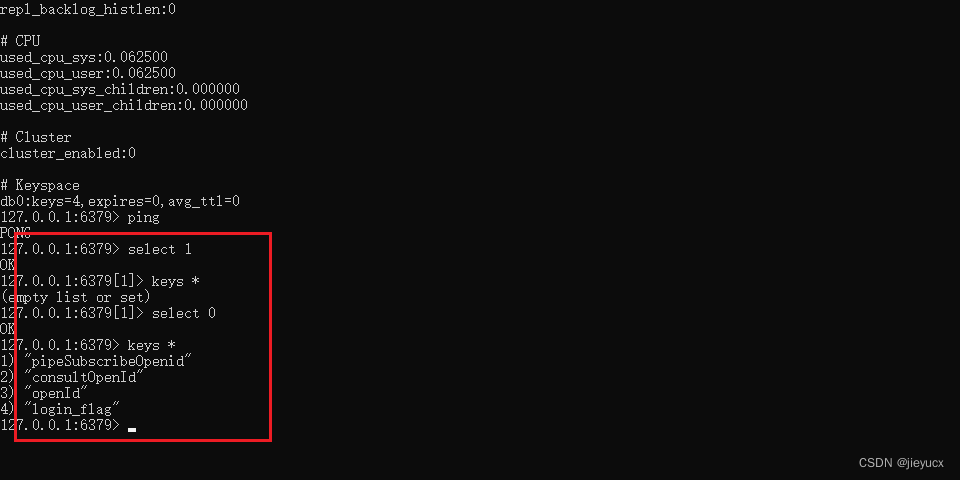
redis基本介绍以及在node中使用
文章目录 引言一、什么是redis1. redis简介2. redis的特点3. redis的应用场景 二、redis在windows下安装1. 下载安装2.验证是否安装成功3. 配置环境变量 三、redis-cli常用命令介绍1. redis-cli2. keys *3. set key value4. get key5. exists key6. del key7. info8. flushdb9.…...

React Native 文本输入基础知识
在 React Native 中提供了一个文本输入组件TextInput。此组件主要是监听键盘输入事件,并把对应的输入值显示在组件中,此组件还提供了很多功能配置参数,例如自动更正、自动大写、占位符文本和不同的键盘类型(例如数字键盘ÿ…...

qt显示图片并转换成灰度图及伪彩图
写了个程序,可在途图片,并切换成灰度图及伪彩图显示,主要代码如下: #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainW…...

oj在线编程输入输出
练习地址:校招笔试真题_C工程师、golang工程师_牛客网 1.读取多行内容 输入描述: 输入包括两个正整数a,b(1 < a, b < 1000),输入数据包括多组。 输出描述: 输出ab的结果输入例子: 1 5 10 20 输出例子: 6 30imp…...

【LeetCode 算法】Add Two Integers 两整数相加-位运算
文章目录 Add Two Integers 两整数相加问题描述:分析代码递归 Tag Add Two Integers 两整数相加 问题描述: 给你两个整数 num1 和 num2,返回这两个整数的和。 − 100 < n u m 1 , n u m 2 < 100 -100 < num1, num2 < 100 −1…...
企业网络日志安全与 EventLog Analyzer
企业的网络日志安全是一项至关重要的任务。随着信息技术的迅猛发展,网络攻击和数据泄露的威胁也与日俱增。为了应对这些威胁,企业需要强大的工具来监控、分析和保护其网络日志。而ManageEngine的EventLog Analyzer正是这样一款卓越的解决方案。 网络日志…...

清风数学建模——拟合算法
拟合算法 文章目录 拟合算法概念 确定拟合曲线最小二乘法的几何解释求解最小二乘法matlab求解最小二乘法如何评价拟合的好坏计算拟合优度的代码 概念 在前面的篇幅中提到可以使用插值算法,通过给定的样本点推算出一定的曲线从而推算出一些想要的值。但存在一些问题…...

单片机 (一) 让LED灯 亮
一:硬件电路图 二:软件代码 #include "reg52.h"#define LED_PORT P2void main() {LED_PORT 0x01; // 0000 0001 D1 是灭的 } #include "reg52.h" 这个头文件的作用:包含52 系列单片机内部所有的功能寄存器 三&#…...

c++——单例模式
c单例模式 1、概念: 单例模式确保一个类只有一个实例,并提供一个全局访问点以获取该实例。这通常通过让类的构造函数为私有,以防止外部直接实例化,然后提供一个静态方法来获取实例。 2、实现方法: 实现单例模式的主…...
——FileStream、BinaryReader、MemorySream、SreamReader等之间的关系)
C# 流Stream详解(2)——FileStream、BinaryReader、MemorySream、SreamReader等之间的关系
【文件流】 电脑上的文件有很多,文本文件、音频文件、视频文件、图片文件等,这些文件会被持久化存储在磁盘上,其本质都是一堆二进制数据。 FileStream用于读取二进制文件。电脑上的所有文件,不管是文本、音频、视频还是其他任意…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
