关于欧拉角你需要知道几个点
基础理解,参照:https://www.cnblogs.com/Estranged-Tech/p/16903025.html
欧拉角、万向节死锁(锁死)理解
一、欧拉角理解
举例讲解
欧拉角用三次独立的绕确定的轴旋转角度来表示姿态。如下图所示

经过三次旋转,旋转角度分别为𝛼、𝛽和 𝛾,由初始的𝑥𝑦𝑧坐标系得到了最终的𝑥‴𝑦‴𝑧‴
坐标系。这就是欧拉角来表示姿态的方法。
如图所示为航空航天中常用的欧拉角,图中的𝜓、𝜃和𝜙
对应于上图中的𝛼、𝛽和 𝛾。

顺规、内旋与外旋
上面所举的例子中,旋转的顺序是按照 𝑧−𝑦−𝑥 的顺序来进行旋转的,并且每一次旋转都是绕自身轴(运动轴)进行的, 这只是欧拉角的一种表示方式。欧拉角共有12种表示方式。
- 顺规
顺规即欧拉角三次转动的顺序规定,欧拉角一共有12种顺规
三个轴只用两个的:Proper Euler angles (z−x−z, x−y−x, y−z−y, z−y−z, x−z−x, y−x−y)
三个轴全都用的:Tait-Bryan angles (x−y−z, y−z−x, z−x−y, x−z−y, z−y−x, y−x−z)
上文举例所用的 𝑧−𝑦−𝑥是三个轴都用的一种顺规,即 先绕𝑧轴旋转,再绕𝑦轴旋转,最后绕𝑥轴旋转。、
- 内旋与外旋
根据绕旋转轴的不同,可以分为内旋和外旋。
内旋 Intrinsic rotations:绕运动轴
外旋 Extrinsic rotations:绕固定轴
上文所举的例子每次旋转都是绕上一次旋转所新产生的坐标轴旋转的(这句话有点绕),比如第二次旋转绕的是𝑦″而不是固定的坐标轴𝑦。所以是绕运动轴,即内旋。
如下图所示,每一次旋转都是绕蓝色的固定轴旋转


如下图所示,每一次旋转都是绕红色(第一张图)、绿色(第二张图)、紫色(第三张图)的运动轴旋转:


在绕轴旋转的时候,顺规有12种,内外旋有2种,但是一般情况下,欧拉角都是说的绕自身轴(运动轴)旋转,即 内旋 。所以欧拉角共有 1×12=12种表示方式。
小结
-
首先说一个很有意思却很不直观的结论:三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同。
-
一般情况下,每一个领域有自己默认的欧拉角定义,也就是24种的其中之一。比如经典力学中使用𝑧𝑥𝑧,量子力学使用的是𝑧𝑦𝑧,航空航天使用𝑧𝑦𝑥或𝑧𝑥𝑦。所以在跨行业或者跨模块协作的时候,一定要问清楚对方是哪一种欧拉角。
二、数学公式

三、万向节死锁理解
- 说明
欧拉角表示姿态的时候,会出现万向节死锁的情况,当我使用传感器(维特智能WT901c-485)读取角度的时候,在𝑍𝑌𝑋的顺规下,当pitch角度为90或-90的时候,roll和yaw角度会乱飘,这就是遇到了万向节的死锁。不同的顺规死锁的情况不一样,本文仅以𝑍𝑌𝑋说明死锁的情况。 - 形象表示
我们以手机为例,说明一下万向节死锁的情况
注意,欧拉角表示姿态时,只能旋转三次,这是理解死锁的前提!
首先这是一个手机,我们对其建立坐标系,平行于手机长边是 𝑋轴,平行于手机短边是 𝑌轴,垂直于桌面是 𝑍轴。我们按照 𝑍-𝑌-𝑋的顺规,对手机进行旋转:

1.首先,先绕 𝑍轴旋转得到 𝑋′𝑌′𝑍′坐标系,如图中绿色所示:

2.然后对 𝑋′𝑌′𝑍′ 绕 𝑌′轴旋转-90°,得到 𝑋″𝑌″𝑍″ ,如图中蓝色所示(此时旋转后的 𝑋″ 轴轴与旋转之前的 𝑍′轴重合)

3.最后将 𝑋″𝑌″𝑍″ 绕 𝑋″轴旋转得到 𝑋‴𝑌‴𝑍‴ 坐标系,如图中黄色所示。

- 这时候重点来了!!!
我们发现,这样旋转过后,手机的长边是与桌面(地面)垂直的,手机的短边是与桌面(地面)平行的。并且,无论第一步转 𝑍轴转了多少度,第三步转 𝑋 轴转了多少度,手机长边与短边都是这个状态。
这就是欧拉角表示角度时的“万向节死锁”现象,按理说欧拉角可以表示三个自由度,即三个方向的旋转。但是在这种情况下,只要𝛽=±90°,无论 𝛼与𝛾怎么取值,手机最终的长边都会与地面垂直,这就好像少了一个自由度,只有2个自由度,所以称之为“万向节死锁”。

- 那么为什么会出现这种情况呢?
一种感性的理解是这样:我们在第二步旋转的时候,将旋转后的 𝑋″ 轴与旋转之前的 𝑍′ 轴重合(这个我在上面旋转演示的时候加粗说明了)。而第一步旋转是绕 𝑍′ 轴旋转的,第三步旋转是绕 𝑋″轴旋转的,所以两轴重合意味着两次旋转绕的是同一个轴,所以说,三个自由度变为了两个自由度。
- 数学解释:

欧拉角与旋转矩阵转换中的相关问题:
- 先出结论:
# ea(人为给定的)转rotmat 再转ea后两个ea的值存在不一致,且含义不一致(主要出现在y角度在一定范围时时),但两个不同的ea可以得到相同的旋转矩阵。
# rotmat转ea再转rotmat(前后rotmat一致)再转ea 前后ea含义是一致的,说明相同的rotmat可以获得一致的ea
# rotmat转ea再转rotmat 前后rotmat是一致的,# 以上说明rotmat到ea是多射,但使用函数进行rotmat转换ea时可以获得一致的ea结果;ea到rotmat是单射。以上说明虽存在多设情况但不影响我们场景的使用。(再验证下)
import torch
import mathdef euler_to_rotation_matrix(euler_angles):"""将欧拉角转为旋转矩阵。欧拉角采用 Z-Y-X顺序 的内旋旋转(与X-Y-Z 的外旋一致)参数:euler_angles:欧拉角,形状为 (batch_size, 3)返回:rotation_matrix:旋转矩阵,形状为 (batch_size, 3, 3)"""# 将欧拉角转为弧度x, y, z = euler_angles[:, 0], euler_angles[:, 1], euler_angles[:, 2]x, y, z = x * torch.pi / 180, y * torch.pi / 180, z * torch.pi / 180# 计算旋转矩阵c_x, s_x = torch.cos(x), torch.sin(x)c_y, s_y = torch.cos(y), torch.sin(y)c_z, s_z = torch.cos(z), torch.sin(z)rotation_matrix_x = torch.stack([torch.ones_like(c_x), torch.zeros_like(c_x), torch.zeros_like(c_x),torch.zeros_like(c_x), c_x, -s_x,torch.zeros_like(c_x), s_x, c_x], dim=1).reshape(-1, 3, 3)rotation_matrix_y = torch.stack([c_y, torch.zeros_like(c_y), s_y,torch.zeros_like(c_y), torch.ones_like(c_y), torch.zeros_like(c_y),-s_y, torch.zeros_like(c_y), c_y], dim=1).reshape(-1, 3, 3)rotation_matrix_z = torch.stack([c_z, -s_z, torch.zeros_like(c_z),s_z, c_z, torch.zeros_like(c_z),torch.zeros_like(c_z), torch.zeros_like(c_z), torch.ones_like(c_z)], dim=1).reshape(-1, 3, 3)rotation_matrix = rotation_matrix_z @ rotation_matrix_y @ rotation_matrix_xreturn rotation_matrixdef rotation_matrix_to_euler(rotation_matrix):"""将旋转矩阵转为欧拉角, 欧拉角采用 Z-Y-X顺序 的内旋旋转(与X-Y-Z 的外旋一致)参数:rotation_matrix:旋转矩阵,形状为 (batch_size, 3, 3)返回:euler_angles:欧拉角,形状为 (batch_size, 3)"""# 计算欧拉角sy = torch.sqrt(rotation_matrix[:, 0, 0] ** 2 + rotation_matrix[:, 1, 0] ** 2)x = torch.atan2(rotation_matrix[:, 2, 1], rotation_matrix[:, 2, 2])y = torch.atan2(-rotation_matrix[:, 2, 0], sy)z = torch.atan2(rotation_matrix[:, 1, 0], rotation_matrix[:, 0, 0])# 将弧度转为角度x, y, z = x * 180 / torch.pi, y * 180 / torch.pi, z * 180 / torch.pi# 组合ea = torch.stack((x, y, z), dim=1)return eaea1=torch.tensor([[ 0., 75., 90.],[ 0., 78., 90.],[ 0., 105., 90.],[ 0., 102., 90.],[ 0., -75., 90.],[ 0., -105., 90.],[ 0., -65., 90.],[ 0., -125., 90.]])
rm1=euler_to_rotation_matrix(ea1)ea2=rotation_matrix_to_euler(rm1)print("有false")
print(ea1==ea2) # 有falserm2=euler_to_rotation_matrix(ea2)
print("全true")
print(rm1-rm2 <0.0001) # q全true相关文章:

关于欧拉角你需要知道几个点
基础理解,参照:https://www.cnblogs.com/Estranged-Tech/p/16903025.html 欧拉角、万向节死锁(锁死)理解 一、欧拉角理解 举例讲解 欧拉角用三次独立的绕确定的轴旋转角度来表示姿态。如下图所示 经过三次旋转,旋…...
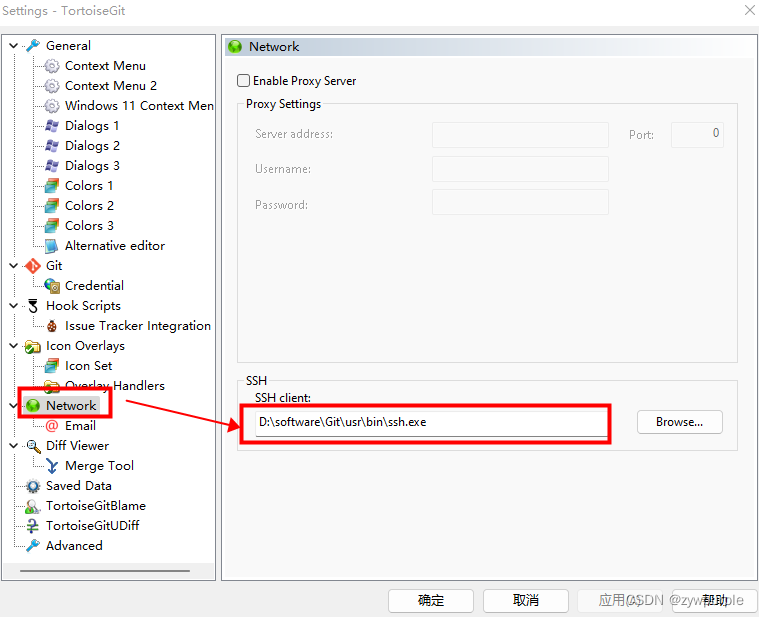
git ssh配置
ssh配置 执行以下命令进行配置 git config --global user.name “这里换上你的用户名” git config --global user.email “这里换上你的邮箱” 执行以下命令生成秘钥: ssh-keygen -t rsa -C “这里换上你的邮箱” 执行命令后需要进行3次或4次确认。直接全部回车就…...
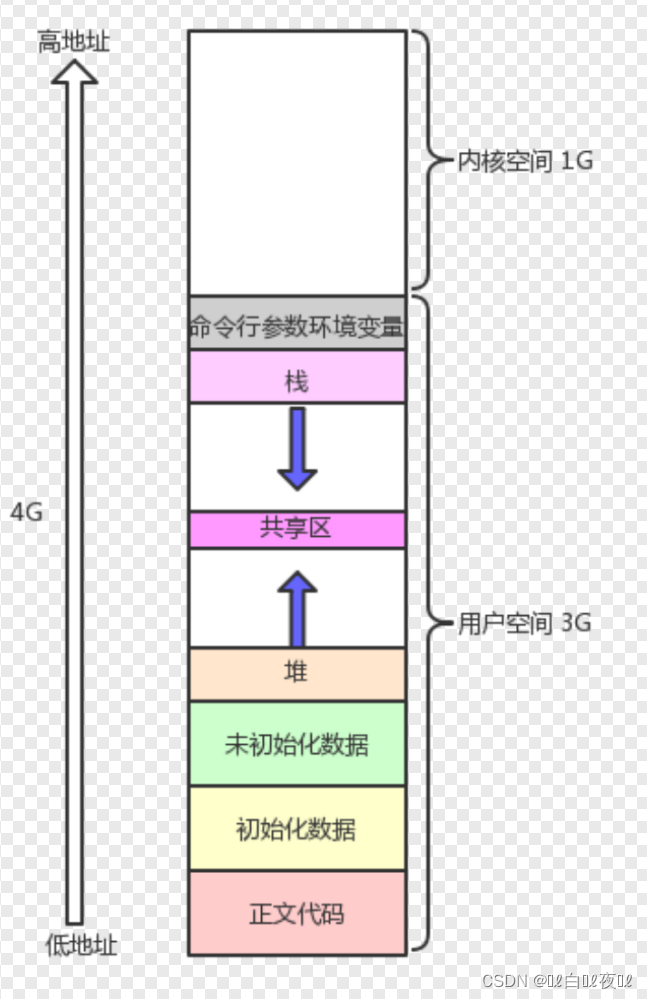
Linux进程概念(三)
环境变量与进程地址空间环境变量什么是环境变量常见环境变量环境变量相关命令环境变量的全局属性PWDmain函数的三个参数进程地址空间什么是进程地址空间进程地址空间,页表,内存的关系为什么存在进程地址空间环境变量 什么是环境变量 我们所有写的程序都…...

新手福利——x64逆向基础
一、x64程序的内存和通用寄存器 随着游戏行业的发展,x32位的程序已经很难满足一些新兴游戏的需求了,因为32位内存的最大值为0xFFFFFFFF,这个值看似足够,但是当游戏对资源需求非常大,那么真正可以分配的内存就显得捉襟…...
)
虚幻c++中的细节之枚举类型(enum)
文章目录前言一、原生c的枚举类型关键字classint8 - 枚举的基础类型(underlying type)二、枚举类型的灵活运用位运算枚举循环遍历三、虚幻风格的枚举类型UENUMUMETATEnumAsByte总结前言 虚幻引擎中的代码部分实现了一套反射机制,为c代码带了…...

判断某个字符串在另一个字符串中的个数
/** * 用于判断字符串中字符的个数 * * param str1 原字符串 * param str2 需要判断的字符 * return 返回有几个 */ private int getCount(String str1, String str2) { //获取两个字符串的长度 int oneLength str1.length(); int toLength str2.length(); //定义两个整数&am…...

测试人员如何运用好OKR
在软件测试工作中是不是还不知道OKR是什么?又或者每次都很害怕写OKR?或者总觉得很迷茫,不知道目标是什么? OKR 与 KPI 的区别 去年公司从KPI换OKR之后,我也有一段抓瞎的过程,然后自己找了两本书看,一本是《OKR工作法》…...

CentOS7 Hive2.3.9 安装部署(mysql 8.0)
一、CentOS7安装MySQL数据库 查询载mariadb rpm -qa | grep mariadb卸载mariadb rpm -e --nodeps [查询出来的内容]安装wget为下载mysql准备 yum -y install wget在tools目录下执行以下命令,下载MySQL的repo源: wget -P /tools/ https://dev.mysql.…...
)
【PTA Advanced】1142 Maximal Clique(C++)
目录 题目 Input Specification: Output Specification: Sample Input: Sample Output: 思路 代码 题目 A clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. A maximal clique is a clique …...

1. MySQL在金融互联网行业的企业级安装部署
这里写目录标题 1. 版本介绍示例2.安装MySQL规范(建议二进制)2.1 安装方式2.2 安装用户2.3 目录规范3.二进制安装3.1 操作系统配置3.2 MySQL 5.7.33 安装部署2.3 MySQL8.0.27安装2.4 源码安装(了解 )3.多实例部署及注意事项3.1 多实例概念3.2 多实例安装3.3 多实例第二种方式…...

【C++修炼之路】19.AVL树
每一个不曾起舞的日子都是对生命的辜负 AVL树前言:一.AVL树的概念二.AVL树的结构2.1 AVL树节点的定义2.2 AVL树的结构2.3 AVL树的插入2.4 AVL树的验证2.5 AVL树的删除(了解)三.AVL树的旋转(重要)3.1 左单旋3.2 右单旋3.3 左右双旋3.4 右左双旋…...
项目管理工具dhtmlxGantt甘特图入门教程(十):服务器端数据集成(下)
这篇文章给大家讲解如何利用dhtmlxGantt在服务器端集成数据。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表,可满足应用程序的所有需求,是完善的甘特图图表库 DhtmlxGantt正版试用下载(qun 764149912)http…...
LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * ... * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k,找出返回能满足 f(x) …...
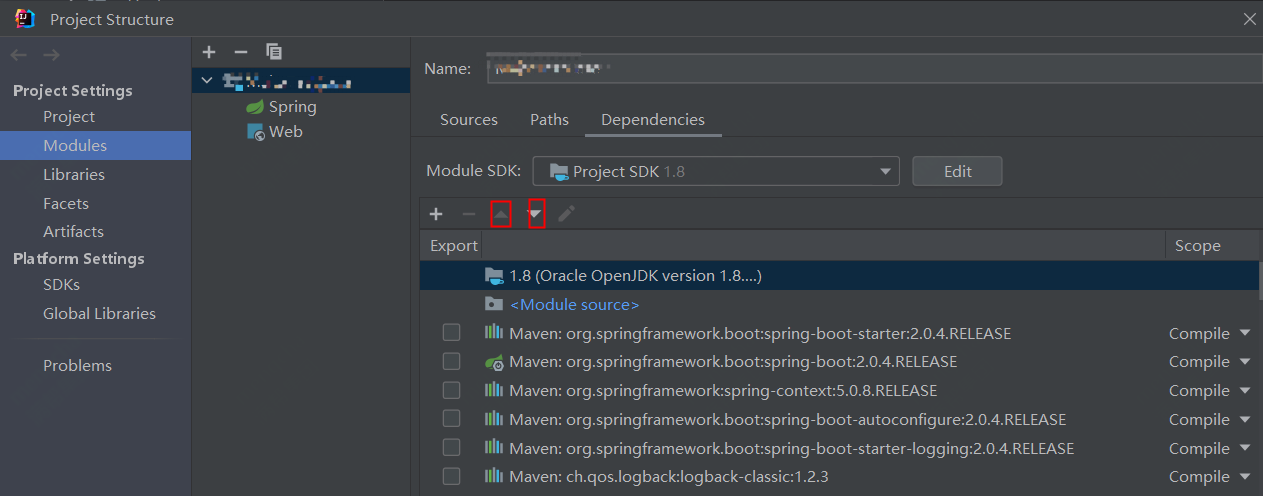
maven打包顺序与jvm类加载顺序
背景:一次dev测试过程中,发现代码中关于jsr303的校验失效,校验类如下,会报一个莫名其妙的运行时错误;遂进行排查。import javax.validation.constraints.NotBlank;Data Accessors(chain true) public class Demo {Not…...

④ 链表
24. 两两交换链表中的节点 题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/ 注意点: 遍历链表的时候什么时候截止(避免空指针异常或无限死循环的问题)? 节点数量为偶数或链表为空时,cur.ne…...
小孩扁桃体肿大3度能自愈吗?6岁小孩扁桃体肥大怎么治效果好?
12月7日,四川眉山市民唐先生说,他刚出生的儿子在妇产医院分娩中心住了20天后感染了败血症。据唐先生介绍,哈子出院时各项指标正常。他在分娩中心住了半个月左右,孩子喝牛奶很生气,第二天就开始发烧了。同一天ÿ…...
【C++提高编程】C++全栈体系(二十二)
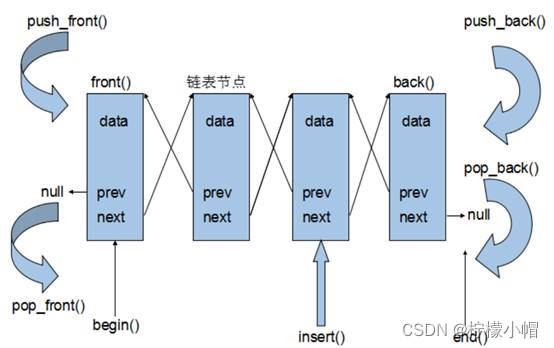
C提高编程 第三章 STL - 常用容器 五、stack容器 1. stack 基本概念 概念:stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口 栈中只有顶端的元素才可以被外界使用,因此栈不允许有遍历行为 栈中进入数据称为 — 入…...
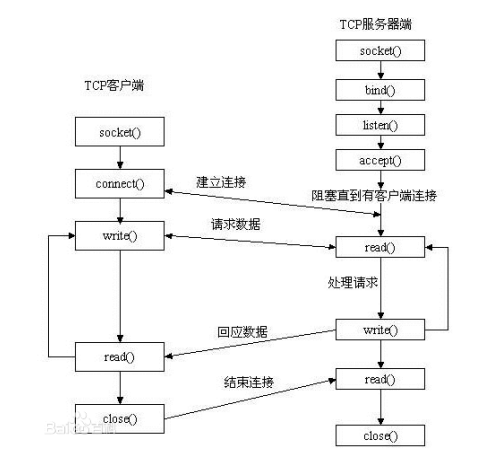
linux系统编程2--网络编程socket知识
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
、join()、yield()和append()函数)
Python-__repr__、__hash__和__eq__方法,split()、join()、yield()和append()函数
1.__repr__方法程序1class Python:passa Python() print(a) print(a.__repr__())结果<__main__.Python object at 0x0000023B82185FD0> <__main__.Python object at 0x0000023B82185FD0>默认情况下,我们得到的信息只会是“类名object at内存地址”程序…...
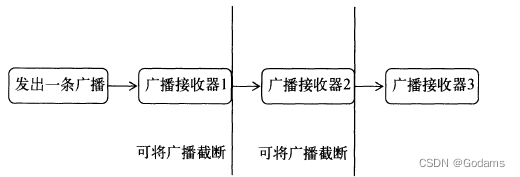
【安卓开发】安卓广播机制
读书笔记系列(第一行代码) 5.1 广播机制简介 标准广播:完全异步执行,广播发出后,所有广播接收器几乎都同一时刻收到这条广播(无法被截断)有序广播:同步执行,广播发出后…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
