【PTA Advanced】1142 Maximal Clique(C++)
目录
题目
Input Specification:
Output Specification:
Sample Input:
Sample Output:
思路
代码
题目
A clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. A maximal clique is a clique that cannot be extended by including one more adjacent vertex. (Quoted from https://en.wikipedia.org/wiki/Clique_(graph_theory))
Now it is your job to judge if a given subset of vertices can form a maximal clique.
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers Nv (≤ 200), the number of vertices in the graph, and Ne, the number of undirected edges. Then Ne lines follow, each gives a pair of vertices of an edge. The vertices are numbered from 1 to Nv.
After the graph, there is another positive integer M (≤ 100). Then M lines of query follow, each first gives a positive number K (≤ Nv), then followed by a sequence of K distinct vertices. All the numbers in a line are separated by a space.
Output Specification:
For each of the M queries, print in a line Yes if the given subset of vertices can form a maximal clique; or if it is a clique but not a maximal clique, print Not Maximal; or if it is not a clique at all, print Not a Clique.
Sample Input:
8 10
5 6
7 8
6 4
3 6
4 5
2 3
8 2
2 7
5 3
3 4
6
4 5 4 3 6
3 2 8 7
2 2 3
1 1
3 4 3 6
3 3 2 1
Sample Output:
Yes
Yes
Yes
Yes
Not Maximal
Not a Clique思路
难度评级:⭐️
代码
#include <iostream>
#include <vector>
#include <set>using namespace std;int matrix[201][201]={0};// 邻接矩阵 int main(int argc, char** argv) {int nv,ne;cin>>nv>>ne;for(int i=0;i<ne;i++) {int a,b;cin>>a>>b;matrix[a][b]=matrix[b][a]=1;}int m;cin>>m;for(int i=0;i<m;i++) {int k;cin>>k;// 输入clique set<int> cliqueSet;vector<int> cliqueVec;for(int j=0;j<k;j++) {int v;cin>>v;cliqueVec.push_back(v);cliqueSet.insert(v);}// 判断clique内的每个顶点之间是否相邻bool isClique=true; for(int j=0;j<k-1;j++) {for(int m=j+1;m<k;m++) {if(matrix[cliqueVec[j]][cliqueVec[m]]==0) {isClique=false;break; }}if(!isClique) break;} if(!isClique) {cout<<"Not a Clique"<<endl;continue;}// 判断是否还可以添加另外的顶点bool isMax=true;for(int j=1;j<=nv;j++) {if(cliqueSet.count(j)==0) {int m;for(m=0;m<k;m++) {if(matrix[j][cliqueVec[m]]==0) break;}if(m>=k) {isMax=false;break;}}} if(!isMax) cout<<"Not Maximal"<<endl;else cout<<"Yes"<<endl;} return 0;
}相关文章:
)
【PTA Advanced】1142 Maximal Clique(C++)
目录 题目 Input Specification: Output Specification: Sample Input: Sample Output: 思路 代码 题目 A clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. A maximal clique is a clique …...

1. MySQL在金融互联网行业的企业级安装部署
这里写目录标题 1. 版本介绍示例2.安装MySQL规范(建议二进制)2.1 安装方式2.2 安装用户2.3 目录规范3.二进制安装3.1 操作系统配置3.2 MySQL 5.7.33 安装部署2.3 MySQL8.0.27安装2.4 源码安装(了解 )3.多实例部署及注意事项3.1 多实例概念3.2 多实例安装3.3 多实例第二种方式…...

【C++修炼之路】19.AVL树
每一个不曾起舞的日子都是对生命的辜负 AVL树前言:一.AVL树的概念二.AVL树的结构2.1 AVL树节点的定义2.2 AVL树的结构2.3 AVL树的插入2.4 AVL树的验证2.5 AVL树的删除(了解)三.AVL树的旋转(重要)3.1 左单旋3.2 右单旋3.3 左右双旋3.4 右左双旋…...
项目管理工具dhtmlxGantt甘特图入门教程(十):服务器端数据集成(下)
这篇文章给大家讲解如何利用dhtmlxGantt在服务器端集成数据。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表,可满足应用程序的所有需求,是完善的甘特图图表库 DhtmlxGantt正版试用下载(qun 764149912)http…...
LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * ... * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k,找出返回能满足 f(x) …...
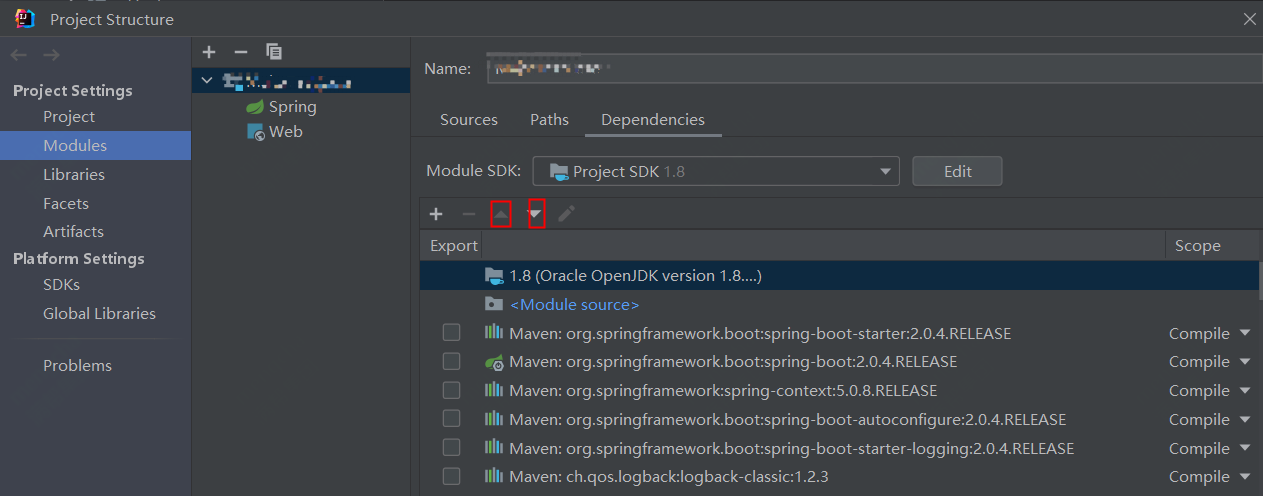
maven打包顺序与jvm类加载顺序
背景:一次dev测试过程中,发现代码中关于jsr303的校验失效,校验类如下,会报一个莫名其妙的运行时错误;遂进行排查。import javax.validation.constraints.NotBlank;Data Accessors(chain true) public class Demo {Not…...

④ 链表
24. 两两交换链表中的节点 题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/ 注意点: 遍历链表的时候什么时候截止(避免空指针异常或无限死循环的问题)? 节点数量为偶数或链表为空时,cur.ne…...
小孩扁桃体肿大3度能自愈吗?6岁小孩扁桃体肥大怎么治效果好?
12月7日,四川眉山市民唐先生说,他刚出生的儿子在妇产医院分娩中心住了20天后感染了败血症。据唐先生介绍,哈子出院时各项指标正常。他在分娩中心住了半个月左右,孩子喝牛奶很生气,第二天就开始发烧了。同一天ÿ…...
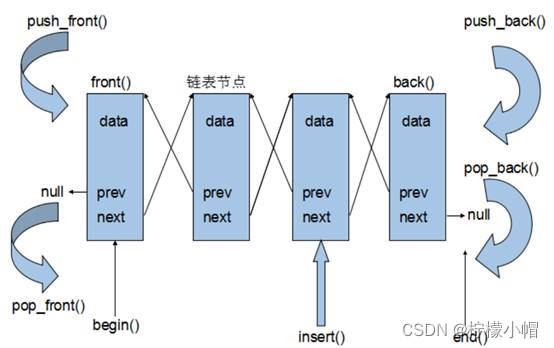
【C++提高编程】C++全栈体系(二十二)
C提高编程 第三章 STL - 常用容器 五、stack容器 1. stack 基本概念 概念:stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口 栈中只有顶端的元素才可以被外界使用,因此栈不允许有遍历行为 栈中进入数据称为 — 入…...
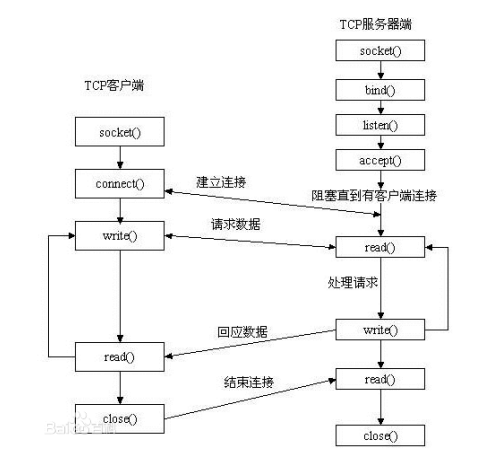
linux系统编程2--网络编程socket知识
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
、join()、yield()和append()函数)
Python-__repr__、__hash__和__eq__方法,split()、join()、yield()和append()函数
1.__repr__方法程序1class Python:passa Python() print(a) print(a.__repr__())结果<__main__.Python object at 0x0000023B82185FD0> <__main__.Python object at 0x0000023B82185FD0>默认情况下,我们得到的信息只会是“类名object at内存地址”程序…...
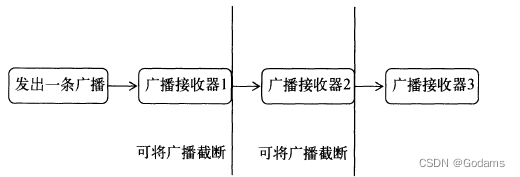
【安卓开发】安卓广播机制
读书笔记系列(第一行代码) 5.1 广播机制简介 标准广播:完全异步执行,广播发出后,所有广播接收器几乎都同一时刻收到这条广播(无法被截断)有序广播:同步执行,广播发出后…...
移动WEB开发四、rem布局
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...
和request.getURI() 以及通过request获得路径相关大全)
request.getURL()和request.getURI() 以及通过request获得路径相关大全
request.getURL()和request.getURI() 如果我的请求是:http://localhost:8080/ServletTest/servlet/Hello request.getRequestURI() 返回值类似:/ServletTest/servlet/Hello request.getRequestURL() 返回值类似:http://localhost:8080/Servle…...
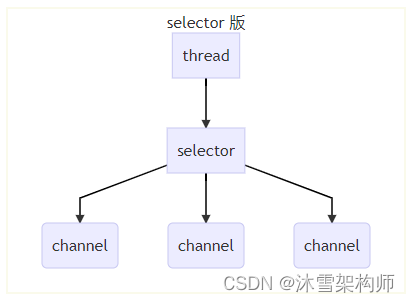
java网络编程-nio学习:阻塞和非阻塞
一、阻塞 阻塞模式下,相关方法都会导致线程暂停 ServerSocketChannel.accept 会在没有连接建立时让线程暂停 SocketChannel.read 会在没有数据可读时让线程暂停 阻塞的表现其实就是线程暂停了,暂停期间不会占用 cpu,但线程相当于闲置 单线…...
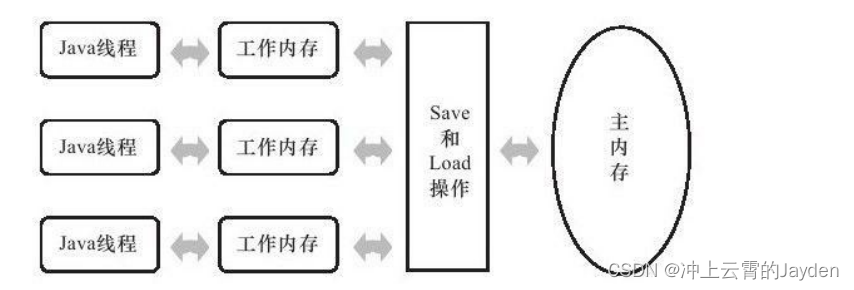
JVM-JMM内存模型(happens-before、volatile)
前言 由于计算机的存储设备与处理器的运算速度有几个数量级的差距所以现代计算机系统都不得不加入一层读写速度尽可能接近处理器运算速度的高速缓存(Cache)来作为内存与处理器之间的缓冲。 将运算需要使用到的数据复制到缓存中,让运算能快速进行,当运算…...

算法leetcode|37. 解数独(rust重拳出击)
文章目录37. 解数独:样例 1:提示:分析:题解:rustgoccpythonjava37. 解数独: 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现…...
SpringBoot整合Dubbo
目录1、dubbo简介2、dubbo解决了什么问题3、环境准备4、项目搭建5、总结springboot整合feign可参考我另外一篇文章SpringBoot集成Feign 1、dubbo简介 Apache Dubbo 最初在 2008 年由 Alibaba 捐献开源,很快成为了国内开源服务框架选型的事实标准框架 ,…...
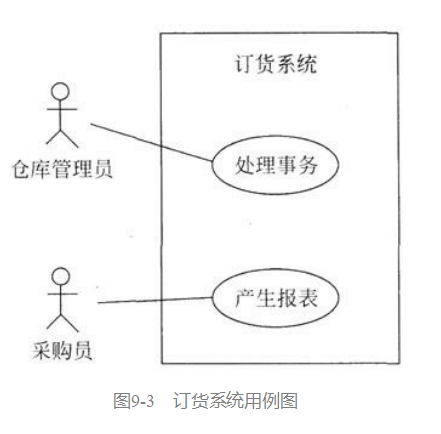
[软件工程导论(第六版)]第9章 面向对象方法学引论(课后习题详解)
文章目录1. 什么是面向对象方法学?它有哪些优点?2. 什么是“对象”?它与传统的数据有何异同?3. 什么是“类”?4. 什么是“继承”?5. 什么是模型?开发软件为何要建模?6. 什么是对象模…...

光学分辨率光声显微镜中基于深度学习的运动校正算法
在这项研究中,我们提出了一种基于深度学习的方法来校正光学分辨率光声显微镜 (OR-PAM) 中的运动伪影。该方法是一种卷积神经网络,它从具有运动伪影的输入原始数据建立端到端映射,以输出校正后的图像。首先,我们进行了仿真研究&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
