【C++修炼之路】19.AVL树
每一个不曾起舞的日子都是对生命的辜负
AVL树
- 前言:
- 一.AVL树的概念
- 二.AVL树的结构
- 2.1 AVL树节点的定义
- 2.2 AVL树的结构
- 2.3 AVL树的插入
- 2.4 AVL树的验证
- 2.5 AVL树的删除(了解)
- 三.AVL树的旋转(重要)
- 3.1 左单旋
- 3.2 右单旋
- 3.3 左右双旋
- 3.4 右左双旋
- 四.AVL树完整代码
- AVLTree.h
- Test.c
- 五. AVL树的性能
前言:
前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N),因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
平衡树有AVL树、红黑树,本篇就来了解一下AVL树。
一.AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:(可以调整是因为相同数据的二叉搜索树不止一种形状)
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
平衡因子 = right - left
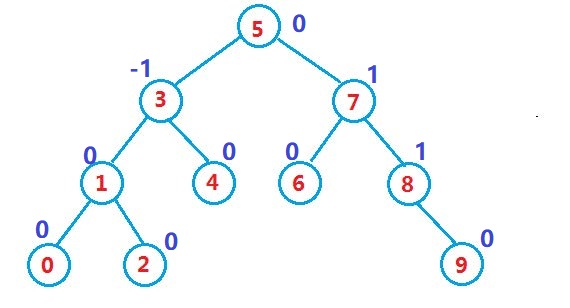
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2n)O(log_2 n)O(log2n),搜索时间复杂度O(log2nlog_2 nlog2n)。
二.AVL树的结构
2.1 AVL树节点的定义
对于AVL树,相比普通的二叉搜索树,最主要的就是多了一个平衡因子保持AVL高度平衡的结构。而为了能够更加便捷的操作平衡因子,除了左右节点的指针,还要新增一个父亲节点指针,即三叉链的结构,因为左右子树的增加节点就会导致父亲节点平衡因子的变化:
template<class K, class V>
struct AVLTreeNode//三叉链
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factor (平衡因子)AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
2.2 AVL树的结构
#pragma once
template<class K, class V>
struct AVLTreeNode//三叉链
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factor (平衡因子)AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K, class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;
public://一系列的成员函数……// 1.插入// 2.
private:Node* _root;
};
2.3 AVL树的插入
对于AVL树的插入来说,本质上还是二叉搜索树,因此大致的插入逻辑还是像普通的搜索树一样,即:比根小向左遍历,比根大向右遍历,如果遇到相同节点,就插入失败,返回false,如果没遇到,遇到空的地方就直接插入。
但与普通二叉搜索树不同的是,我们在插入节点的过程中要时时刻刻注意AVL树的结构,即通过我们新增的成员:平衡因子_bf,而为了便于访问这个平衡因子相比较普通的搜索树也就增加了指向父亲节点的指针,即三叉链的结构。但需要注意的是,如果插入了新节点,这样不仅会导致父亲节点平衡因子的变化,同样也有可能父亲的父亲节点也会跟着变化,下面试着举2个例子:
例1: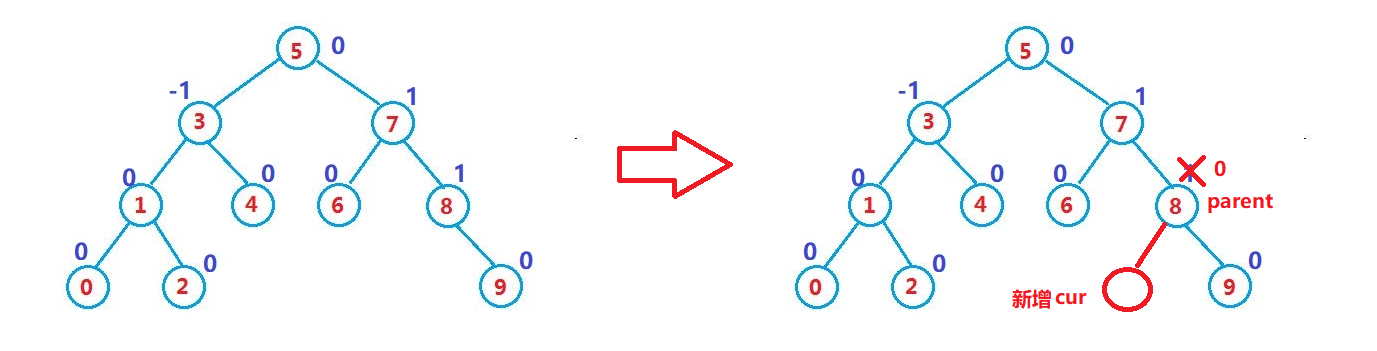
对于这种情况来说,新增了一个cur节点,恰好能够使parent的平衡因子变成0,我们知道平衡因子=右子树的高度-左子树的高度,我们可以看出,parent的值从-1或者1变成0,整颗树没有任何一个子树的高度发生了变化,因此插入一个节点不影响任何子树的高度,即parent的平衡因子变成0,就不需要继续向上遍历检索上面父亲节点的平衡因子了。
例2:
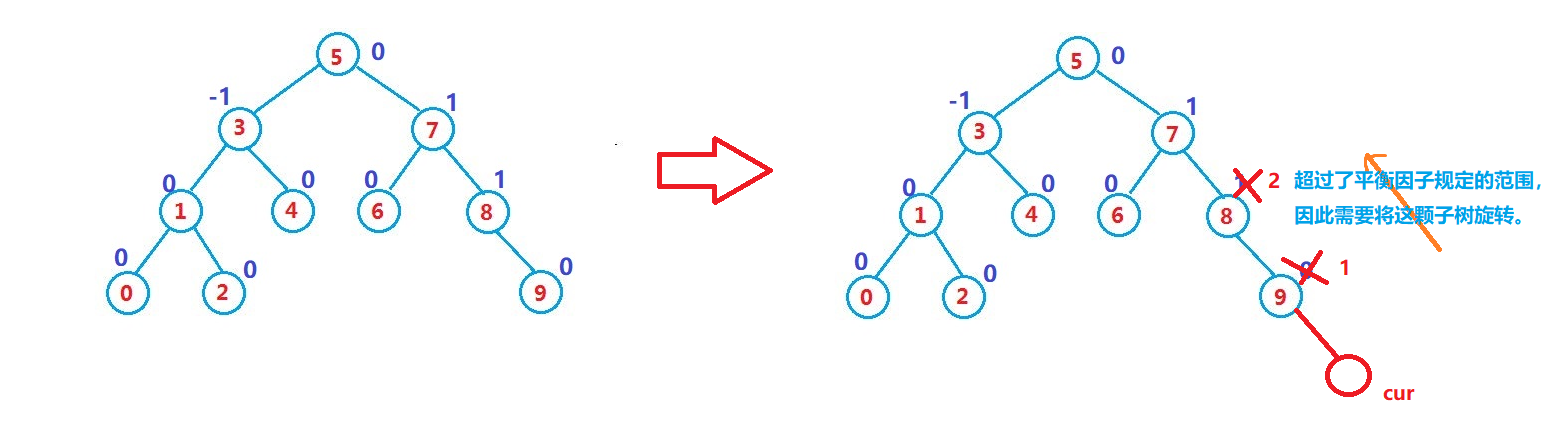
新增插入节点时,都必须去检索。对于这种情况,向上遍历的平衡因子并且根据变化的结构去修改平衡因子,如果平衡因子变成了不属于[-1, 1]的范围,那就说明这颗子树的结构出现了问题,此时就需要将这颗子树进行旋转,使其结构满足所有平衡因子都属于[-1, 1]的范畴。如何旋转?由于旋转过于复杂,后面会单独展示。
+++
那再缕清一下插入的思路:
第一步:寻找插入点
- 此步骤与普通的二叉搜索树的规则几乎相同,唯一区别是由于多了一个parent指针,parent初始化为nullptr,因此在搜索的时候parent也需要不断变化。
第二步:更新平衡因子
- parent的平衡因子会随着插入节点而发生变化,parent一旦变化,那parent的parent也会发生变化,因此需要一个循环使平衡因子顺着自己的parent指针不断遍历,并且判断是否需要更改。
第三步:判断平衡因子的范围
- 平衡因子如果变成0,说明之前的
parent->_bf是1或-1,说明之前parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新,可以跳出循环。 - 平衡因子如果变成1或者-1,说明插入之前
parent->_bf= 0,两遍一样高,现在插入后一边更高了,parent所在子树高度变了,需要继续往上更新 - 平衡因子如果变成 2或者-2,说明之前
parent->_bf是1或-1,现在插入后严重不平衡,违反了左右高度差不超过1的规则,就需要就地处理,即旋转这颗子树,旋转需要注意:- 让这颗子树旋转之后的高度差不超过1。
- 旋转过程中需要保持仍是搜索树。
- 更新调整孩子节点的平衡因子。
- 让这颗子树的高度和插入前保持一致。
Insert代码:
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent){//新增在右:parent->_bf++//新增在左:parent->_bf--if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//判断平衡因子的范围if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要旋转这个子树:代码和情况过多,在三.AVL树的旋转中展示:}else{assert(false);}}return true;}
看完这部分代码直接看下一个一级标题:AVL树的旋转。看完旋转之后再回来按照顺序依次看。
2.4 AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
- 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
- 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
代码如下:
int Height(Node* root)
{if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;
}bool IsBalance()
{return IsBalance(_root);
}bool IsBalance(Node* root)
{if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf)//这一步可以进一步验证平衡因子是否准确,不写也无所谓{cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);
}
2.5 AVL树的删除(了解)
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。可以想象成插入的反向思考,具体实现可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
删除太难了,别学了。
三.AVL树的旋转(重要)
旋转就是降低高度。
在2.3的插入中,我们说到了一旦平衡因子超出了指定的范围就会导致子树左右高度差发生变化,导致结构不再是高度平衡的状态,此时这个子树就需要旋转,旋转到没插入前的高度。对于旋转,有很多种情况,因此我把他单独拿出来作为一个大标题的形式来描述。
先不进行分类,随便举个例子看看: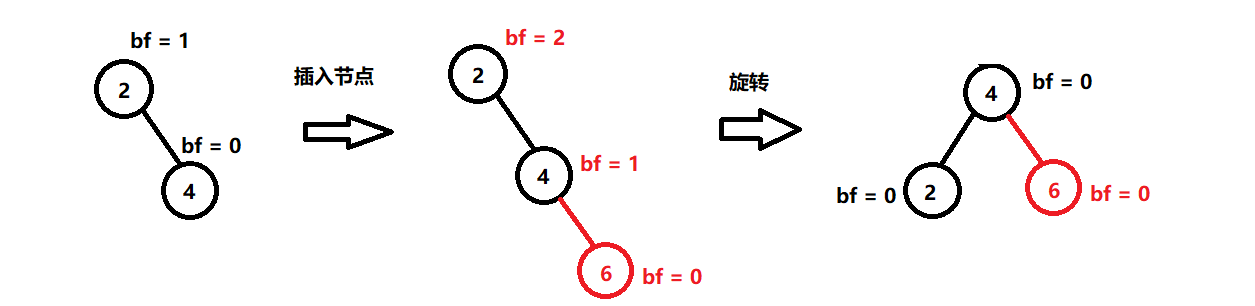
可以看出,旋转后的特征:
- 让这颗子树旋转之后的高度差不超过1。
- 旋转过程中需要保持仍是搜索树。
- 更新调整孩子节点的平衡因子。
- 让这颗子树的高度和插入前保持一致。
但实际上,我们的AVL树可能会非常的复杂,因此并不像上面的例子那么简单。
因此,如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转根据不同的插入情况分为四种:左单旋、右单旋、先左单旋再右单旋、先右单旋再左单旋。上面的例子就属于左单旋。
- 注:插入的节点名字为cur。
3.1 左单旋
- 新节点插入较高右子树的右侧—右右:左单旋
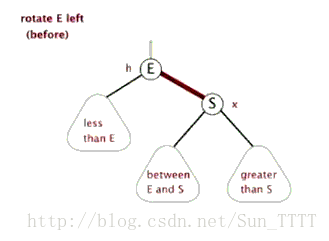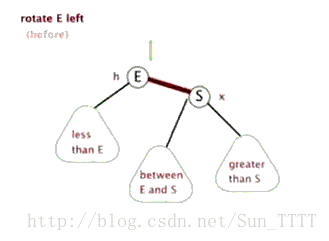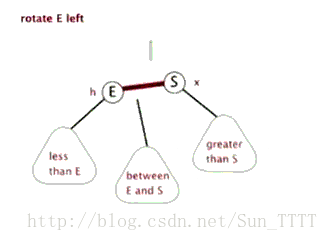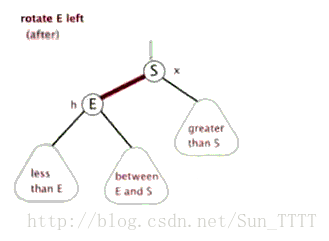
a, b, c都为AVL树,且高度为h.
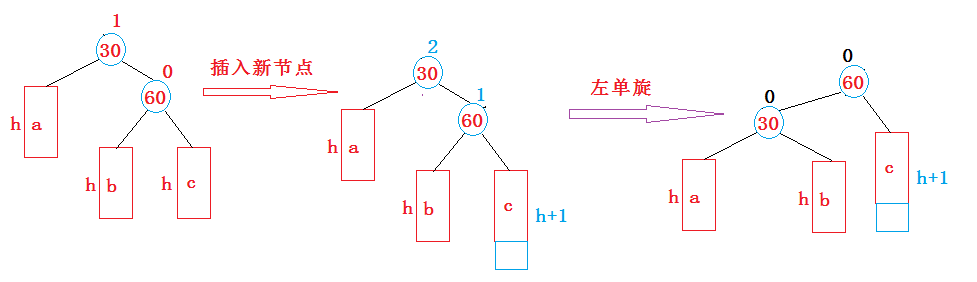
对于此图,实际上是一个抽象图,即a,b,c的高度都不是一个确切的数字。但从图中我们可以看出,在c插入节点,导致高度变化为h+1,这个时候30的平衡因子就变成了2。那为什么会左旋,从抽象的角度来看,对于高度平衡的AVL树,右边过高,我们就需要考虑不让右面高,从绳子的角度来说,右边过长,那就将中间节点再往右移动,对于这个模型也一样,我们考虑根节点往右移动,即将60作为根节点,此时左子树就会往下,可以看出,这是一个将左子树往下压的过程,通过这种角度的思考,就不难对这种树进行旋转。
既然有了抽象的左旋,从学习的角度同样要将这种AVL树的旋转具象化:
-
如果h=0,那情况就正如我们一开始随便举的例子一样,如果是根节点的1平衡因子不符合条件,那就将右孩子通过旋转变成根节点,右孩子的左孩子给到原来根节点的右孩子节点,这样就完成了旋转,同时满足了条件。
-
如果h=1,唯一与上面的情况不同的是,平衡因子首先不满足条件的节点可能不会是根节点,因此这种情况,我们只需将这个不满足条件的节点作为需要旋转的子树的根,就和上面的步骤一样。最后这个子树的新根的parent指针再连接回去。需要注意的细节问题是节点的parent指针。
-
如果h=2,那么情况就会变的很复杂,因此上述抽象的结构我们提前将c确定形状,在这我们具体实例化一下:
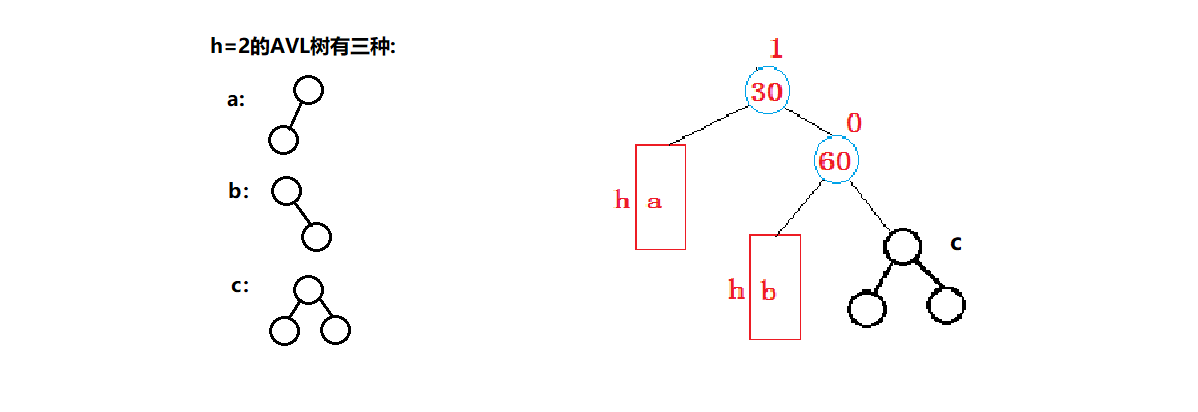
对于红色的a, b来说,都有三种的选择,因此当h=2时插入之前的组合情况就会有
3*3=9种的结果,在这种情况之下,在c的任何一个子树下插入都会引发30这个节点的旋转,而c的孩子节点有四个位置可以插入,那一共就是9*4=36种情况。h继续增加只会更多,因此也没必要将这么多种情况都画出来,因为这些情况都属于上面抽象图的衍生,都可以调用左旋转。
+++
左单旋平衡因子的条件:
if (parent->_bf == 2 && cur->_bf == 1)
{RotateL(parent);//左单旋
}
知道旋转的方法之后,我们还需要将这种情况的具体步骤给总结出来: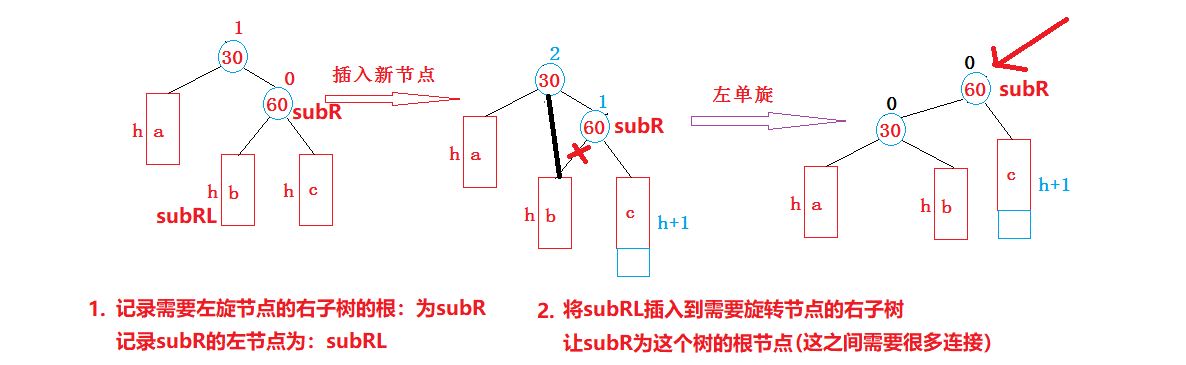
左单旋代码:
void RotateL(Node* parent)//左单旋
{//1.记录subR, subRLNode* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)//subRL不为空则需要连接到parent{subRL->_parent = parent;}subR->_left = parent;Node* ppNode = parent->_parent;//记录保存parent->_parent = subR;if (ppNode == nullptr)//说明根节点变化{_root = subR;_root->_parent = nullptr;}else//如果是局部子树{//判断ppNode之前是左连接还是右连接if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}//最后更新平衡因子:一定都为0parent->_bf = subR->_bf = 0;
}
3.2 右单旋
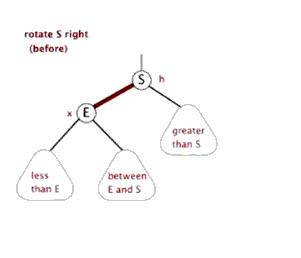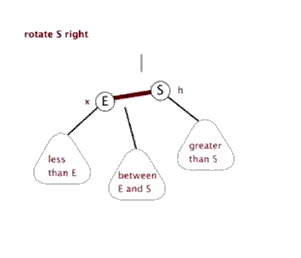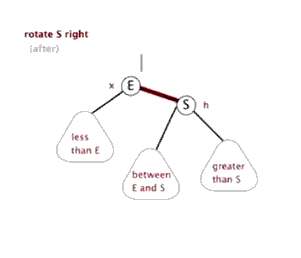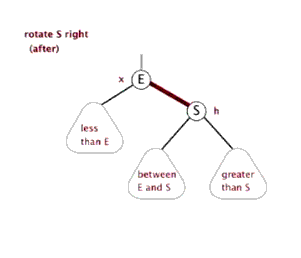
- 新节点插入较高左子树的左侧—左左:右单旋
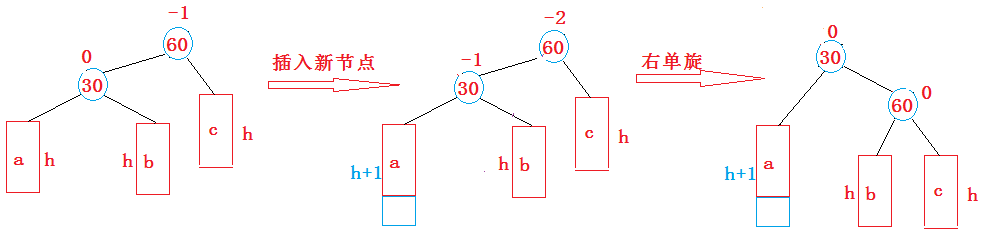
右单旋平衡因子的条件:
if (parent->_bf == -2 && cur->_bf == -1)
{RotateR(parent);//右单旋
}
和左单旋的思想是一样的,只不过是将赋值的左右反过来。这里就直接上代码了:
void RotateR(Node* parent)//右单旋
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent == nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right == subL;}subL->_parent = ppNode;}//最后更新平衡因子subL->_bf = parent->_bf = 0;
}
可以看出,左单旋和右单旋是非常类似的,都是类似于这样: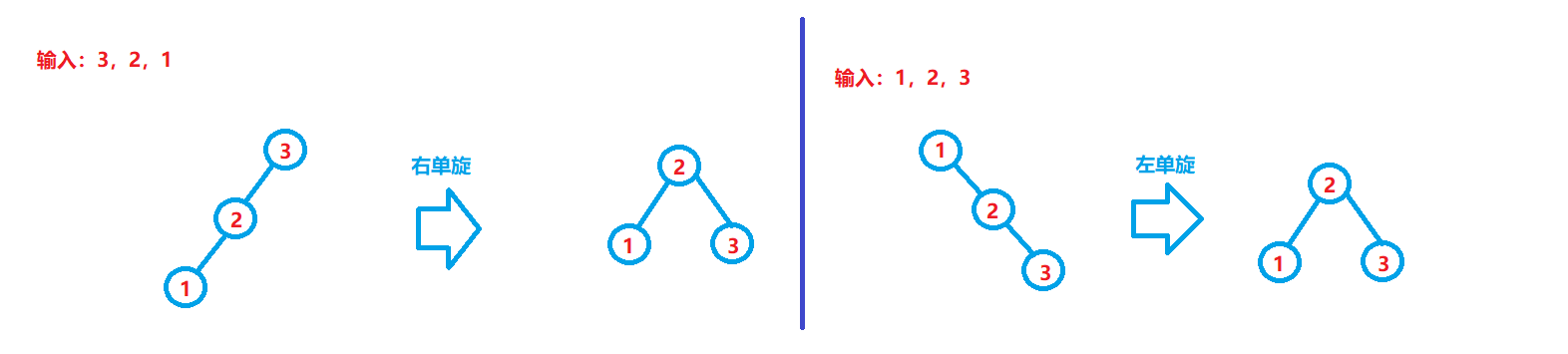
那如果不是按照上面的样子插入,即有拐点呢?
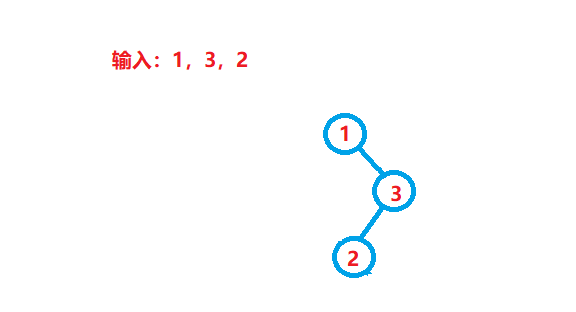
这种折线似的结构似乎更加常见,但如果仍用山上面的左旋或者右旋,只会让其左右转一下,并不能减少其任意子树的高度。这样就无法用到上面任何一个单旋了,因此下面还有两种旋转处理的情况。
3.3 左右双旋
- 新节点插入较高左子树的右侧—左右:先左单旋再右单旋
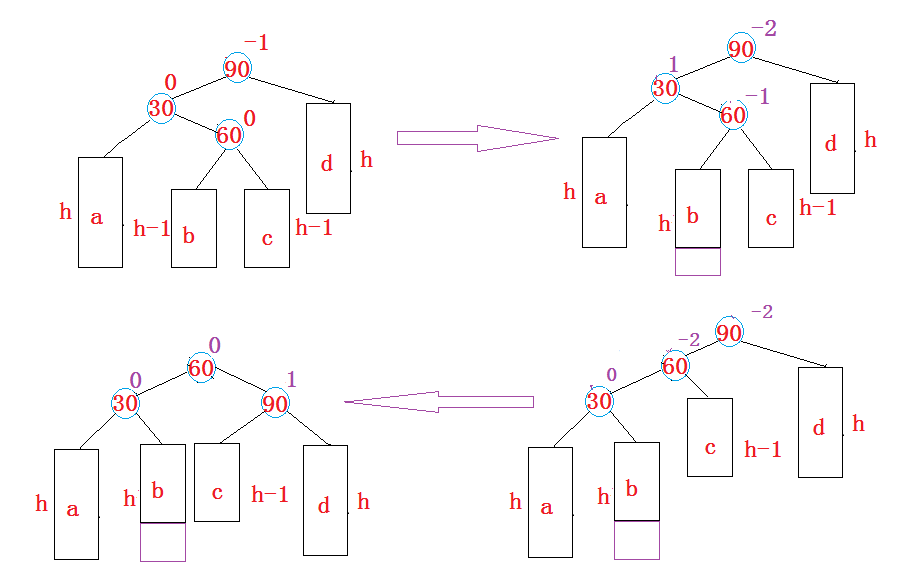
就如上面的抽象图,我们仍然需要对其有所见解才能进一步分析并写出代码,通过观察发现对具象的三个节点,原本是折线,通过左旋变成直线后,发现就可以通过右旋从而实现AVL树的结构了。当然,这么说还是过于敷衍,下面将h具象化看看例子:
- 如果h=0,则h-1的部分为-1,但我们可以同样的认为他是不存在节点的:

- 如果h=1,和上面的情况几乎相似,同3.1左单旋叙述的一样,只是子树部分旋转,需要注意parent指针,这种情况是最普遍的。
- 如果h=2,情况就如左单旋的h=2的情况一样,有非常多的情况出现,因此,这里只需明白抽象的具体树的旋转规则,就可以了。
+++
左右双旋平衡因子的条件:
if (parent->_bf == -2 && cur->_bf == 1)
{RotateLR(parent);
}
下面来看看左右双旋的具体步骤:
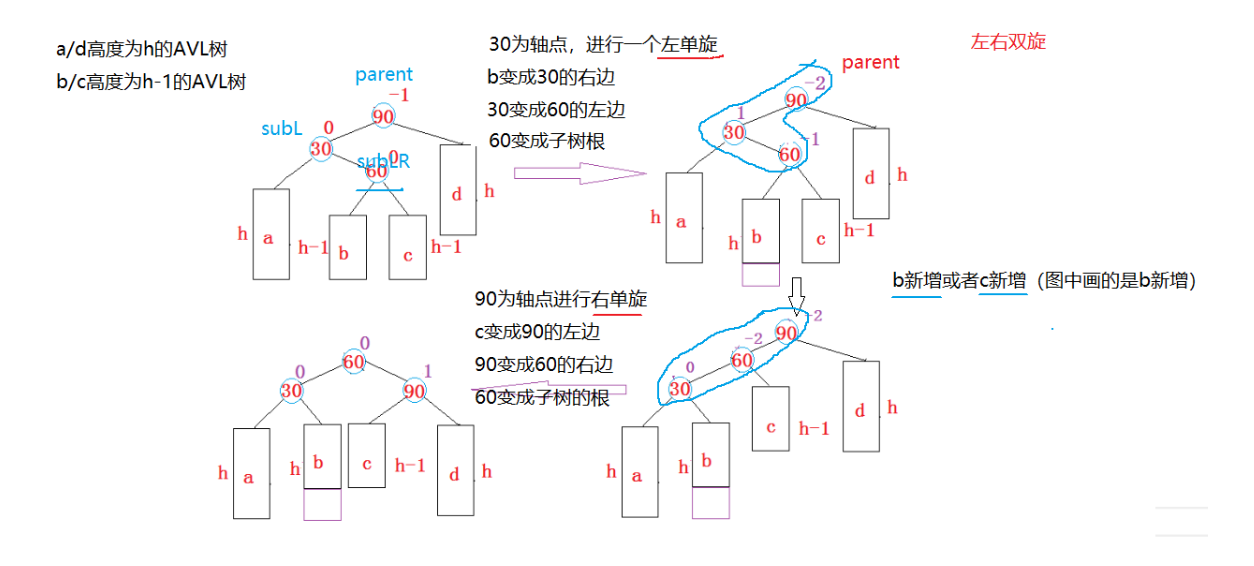
-
对于左右双旋,上面的步骤不难看出,先左旋parent的左孩子,之后再右单旋旋转parent,复用前面的左单旋和右单旋的代码即可。
-
但是关键还要修改旋转节点对应的平衡因子,由于左单旋和右单旋改变了原有的平衡因子,因此我们需要在左右单旋之前将需要改变的节点及对应的平衡因子的值给保留起来,保留的目的是需要根据原有的平衡因子的值将旋转后对应的值进行改变。
-
如果插入后
subLR->_bf == -1,即subLR的左子树插入,上图就是这样,旋转后的parent->_bf = 1,subL->_bf = 0,subLR->_bf = 0 -
如果插入后
subLR->_bf == 1,即subLR的右子树插入,那么旋转后的parent->_bf = 0,subL->_bf = -1,subLR->_bf = 0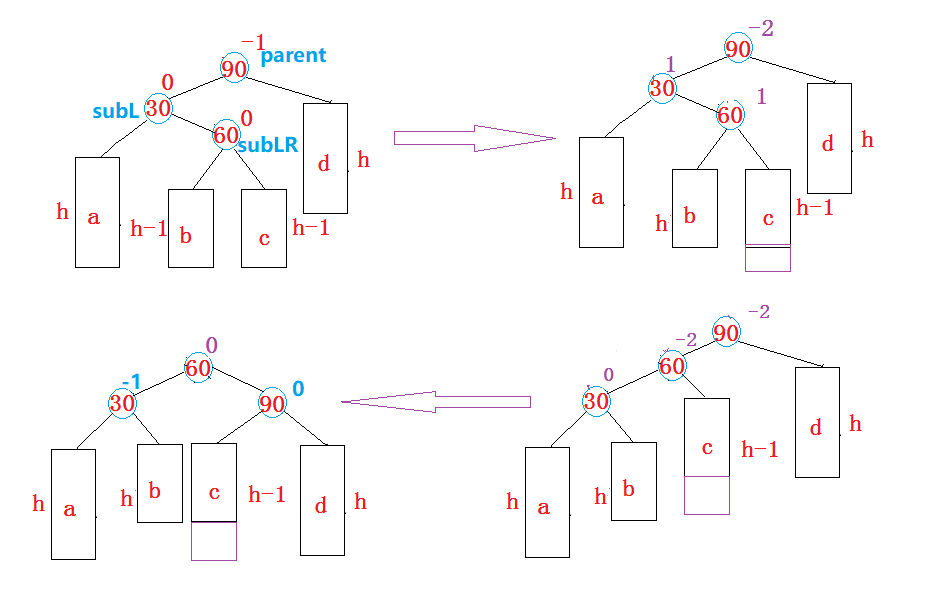
-
如果插入后的
subLR->_bf == 0,说明subLR本身就是新增节点,则这三个平衡因子都为0。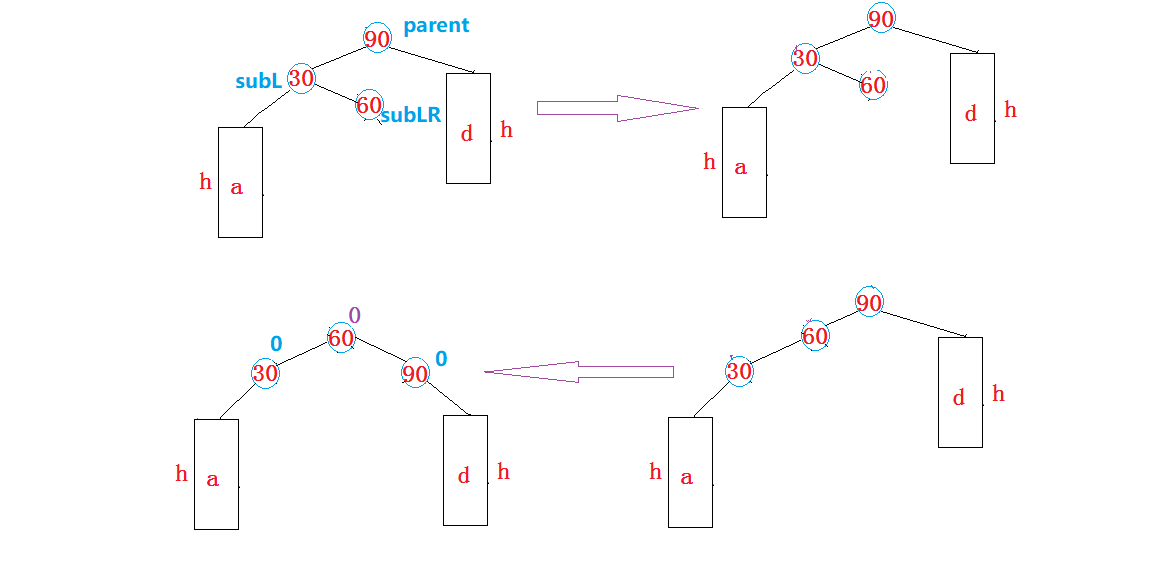
-
代码:
void RotateLR(Node* parent)//左右双旋
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);//左节点左旋RotateR(parent);//右旋//改变平衡因子if (bf == 1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == -1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 0)//自己新增{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}
可以看出,左右双旋的平衡因子的更新才是关键。
3.4 右左双旋
- 新节点插入较高右子树的左侧—右左:先右单旋再左单旋
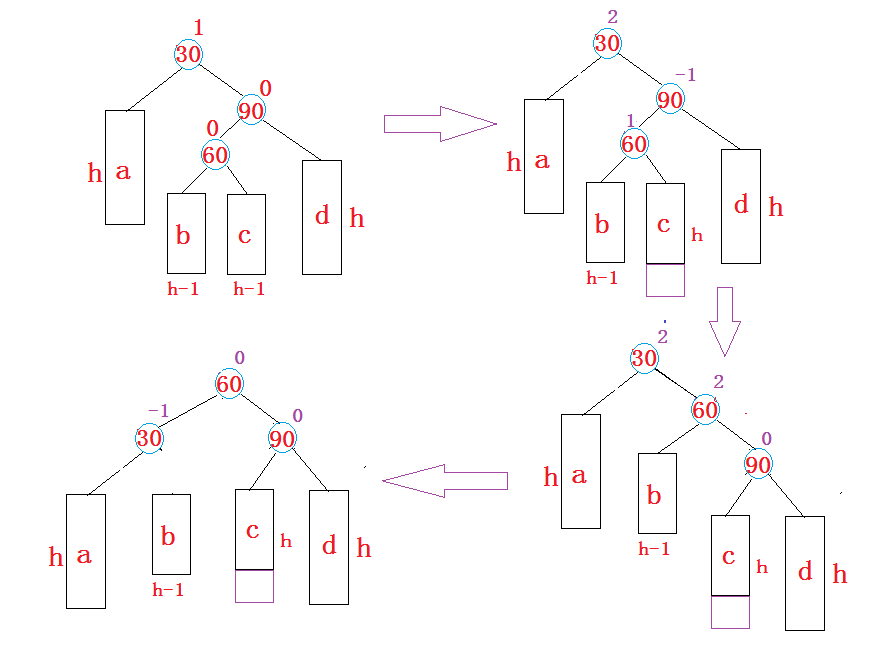
正如右单旋按照左单旋的思路,右左双旋就按照左右双旋的思路。
按照不同的情况画图就能准确的判断平衡因子的变化。
void RotateRL(Node* parent)//右左双旋
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);//右节点右旋RotateL(parent);//左旋//改变平衡因子if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}
四.AVL树完整代码
AVLTree.h
#pragma oncetemplate<class K, class V>
struct AVLTreeNode//三叉链
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factor (平衡因子)AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K, class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent){//新增在右:parent->_bf++//新增在左:parent->_bf--if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//判断平衡因子的范围if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要旋转这个子树if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);//左旋}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);//右旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{cout << parent->_kv.first << ":" << parent->_bf << ":" << cur->_bf << endl;assert(false);}break;}else{assert(false);}}return true;}void RotateL(Node* parent)//左单旋{//1.记录subR, subRLNode* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)//subRL不为空则需要连接到parent{subRL->_parent = parent;}Node* ppNode = parent->_parent;//记录保存subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr)//说明根节点变化{_root = subR;_root->_parent = nullptr;}else//如果是局部子树{//判断ppNode之前是左连接还是右连接if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}//最后更新平衡因子:一定都为0parent->_bf = subR->_bf = 0;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//最后更新平衡因子subL->_bf = parent->_bf = 0;}void RotateLR(Node* parent)//左右双旋{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);//左节点左旋RotateR(parent);//右旋//改变平衡因子if (bf == 1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == -1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent)//右左双旋{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);//右节点右旋RotateL(parent);//左旋//改变平衡因子if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;//改正subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}void Inorder(){_Inorder(_root);}int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}private:void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}Node* _root = nullptr;
};void TestAVLTree()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.Inorder();}
Test.c
#include<iostream>
#include<map>
#include<string>
#include<assert.h>
using namespace std;
#include"AVLTree.h"int main()
{TestAVLTree();return 0;
}

五. AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log2(N)log_2 (N)log2(N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

【C++修炼之路】19.AVL树
每一个不曾起舞的日子都是对生命的辜负 AVL树前言:一.AVL树的概念二.AVL树的结构2.1 AVL树节点的定义2.2 AVL树的结构2.3 AVL树的插入2.4 AVL树的验证2.5 AVL树的删除(了解)三.AVL树的旋转(重要)3.1 左单旋3.2 右单旋3.3 左右双旋3.4 右左双旋…...
项目管理工具dhtmlxGantt甘特图入门教程(十):服务器端数据集成(下)
这篇文章给大家讲解如何利用dhtmlxGantt在服务器端集成数据。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表,可满足应用程序的所有需求,是完善的甘特图图表库 DhtmlxGantt正版试用下载(qun 764149912)http…...
LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * ... * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k,找出返回能满足 f(x) …...
maven打包顺序与jvm类加载顺序
背景:一次dev测试过程中,发现代码中关于jsr303的校验失效,校验类如下,会报一个莫名其妙的运行时错误;遂进行排查。import javax.validation.constraints.NotBlank;Data Accessors(chain true) public class Demo {Not…...

④ 链表
24. 两两交换链表中的节点 题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/ 注意点: 遍历链表的时候什么时候截止(避免空指针异常或无限死循环的问题)? 节点数量为偶数或链表为空时,cur.ne…...
小孩扁桃体肿大3度能自愈吗?6岁小孩扁桃体肥大怎么治效果好?
12月7日,四川眉山市民唐先生说,他刚出生的儿子在妇产医院分娩中心住了20天后感染了败血症。据唐先生介绍,哈子出院时各项指标正常。他在分娩中心住了半个月左右,孩子喝牛奶很生气,第二天就开始发烧了。同一天ÿ…...
【C++提高编程】C++全栈体系(二十二)
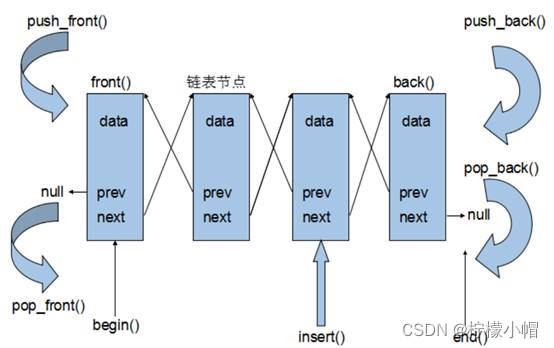
C提高编程 第三章 STL - 常用容器 五、stack容器 1. stack 基本概念 概念:stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口 栈中只有顶端的元素才可以被外界使用,因此栈不允许有遍历行为 栈中进入数据称为 — 入…...
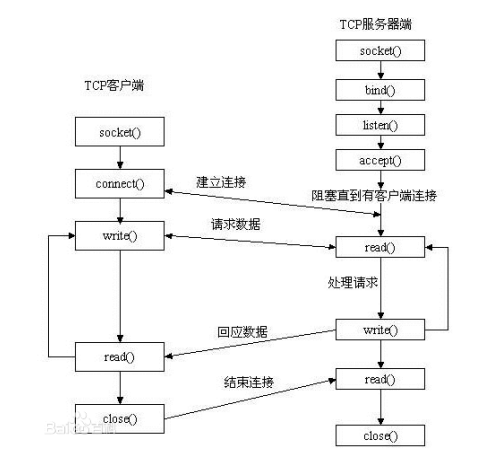
linux系统编程2--网络编程socket知识
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
、join()、yield()和append()函数)
Python-__repr__、__hash__和__eq__方法,split()、join()、yield()和append()函数
1.__repr__方法程序1class Python:passa Python() print(a) print(a.__repr__())结果<__main__.Python object at 0x0000023B82185FD0> <__main__.Python object at 0x0000023B82185FD0>默认情况下,我们得到的信息只会是“类名object at内存地址”程序…...
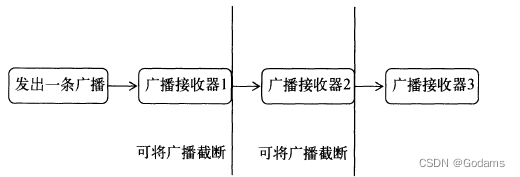
【安卓开发】安卓广播机制
读书笔记系列(第一行代码) 5.1 广播机制简介 标准广播:完全异步执行,广播发出后,所有广播接收器几乎都同一时刻收到这条广播(无法被截断)有序广播:同步执行,广播发出后…...
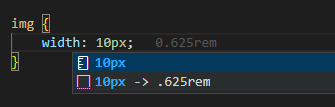
移动WEB开发四、rem布局
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...
和request.getURI() 以及通过request获得路径相关大全)
request.getURL()和request.getURI() 以及通过request获得路径相关大全
request.getURL()和request.getURI() 如果我的请求是:http://localhost:8080/ServletTest/servlet/Hello request.getRequestURI() 返回值类似:/ServletTest/servlet/Hello request.getRequestURL() 返回值类似:http://localhost:8080/Servle…...
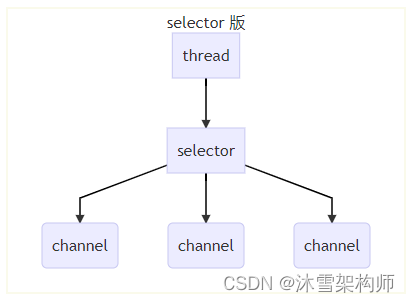
java网络编程-nio学习:阻塞和非阻塞
一、阻塞 阻塞模式下,相关方法都会导致线程暂停 ServerSocketChannel.accept 会在没有连接建立时让线程暂停 SocketChannel.read 会在没有数据可读时让线程暂停 阻塞的表现其实就是线程暂停了,暂停期间不会占用 cpu,但线程相当于闲置 单线…...
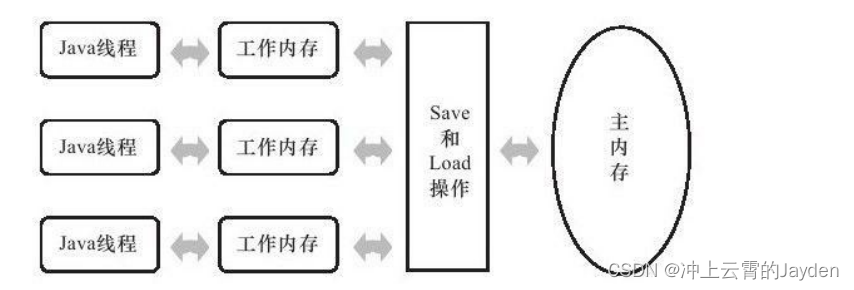
JVM-JMM内存模型(happens-before、volatile)
前言 由于计算机的存储设备与处理器的运算速度有几个数量级的差距所以现代计算机系统都不得不加入一层读写速度尽可能接近处理器运算速度的高速缓存(Cache)来作为内存与处理器之间的缓冲。 将运算需要使用到的数据复制到缓存中,让运算能快速进行,当运算…...

算法leetcode|37. 解数独(rust重拳出击)
文章目录37. 解数独:样例 1:提示:分析:题解:rustgoccpythonjava37. 解数独: 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现…...
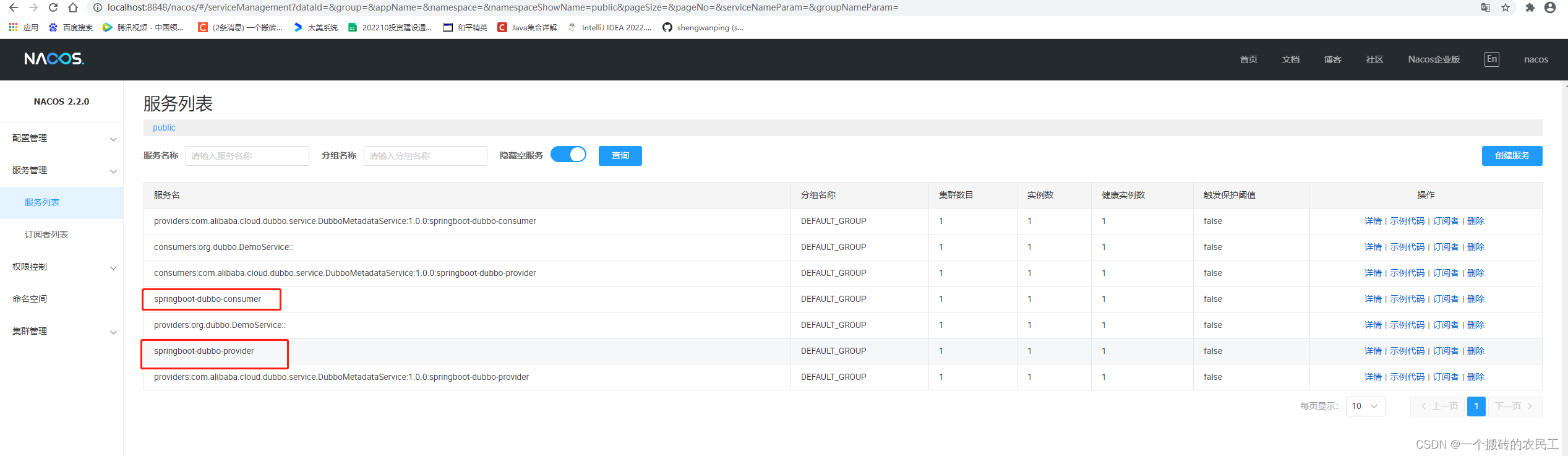
SpringBoot整合Dubbo
目录1、dubbo简介2、dubbo解决了什么问题3、环境准备4、项目搭建5、总结springboot整合feign可参考我另外一篇文章SpringBoot集成Feign 1、dubbo简介 Apache Dubbo 最初在 2008 年由 Alibaba 捐献开源,很快成为了国内开源服务框架选型的事实标准框架 ,…...
[软件工程导论(第六版)]第9章 面向对象方法学引论(课后习题详解)
文章目录1. 什么是面向对象方法学?它有哪些优点?2. 什么是“对象”?它与传统的数据有何异同?3. 什么是“类”?4. 什么是“继承”?5. 什么是模型?开发软件为何要建模?6. 什么是对象模…...

光学分辨率光声显微镜中基于深度学习的运动校正算法
在这项研究中,我们提出了一种基于深度学习的方法来校正光学分辨率光声显微镜 (OR-PAM) 中的运动伪影。该方法是一种卷积神经网络,它从具有运动伪影的输入原始数据建立端到端映射,以输出校正后的图像。首先,我们进行了仿真研究&…...

浅谈UG二次开发中使用的FindObject
一般我们在业务逻辑里想查找一个Object的时候,会调用FindObject、GetObject、NxObjectManager.Get,不管是上述哪种实现,都是在内存中找东西,找到了就返回对象,否则返回null,但不会触发加载。 这里我分别从建…...

贪心原理及刷题
更新中 概念 使用贪心需要满足,上一步的局部最优解能推出这一步的局部最优解,直到得到全局最优解 而dp这一步的局部最优,不一定来源上一步的局部最优,而可能与更早的解有关,同时dp转移方程的推导也比较复杂 122. 买卖股票的最佳时机 II - 力扣(LeetCode) 这道题是典…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

