LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! = 1 * 2 * 3 * ... * x,且 0! = 1 。
例如, f(3) = 0 ,因为 3! = 6 的末尾没有 0 ;而 f(11) = 2 ,因为 11!= 39916800 末端有 2 个 0 。
给定 k,找出返回能满足 f(x) = k 的非负整数 x 的数量。
示例 1:
输入:k = 0
输出:5
解释:0!, 1!, 2!, 3!, 和 4! 均符合 k = 0 的条件。
示例 2:
输入:k = 5
输出:0
解释:没有匹配到这样的 x!,符合 k = 5 的条件。
示例 3:
输入: k = 3
输出: 5
提示:
0 <= k <= 10^9
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/preimage-size-of-factorial-zeroes-function
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这个题简单的一匹。。
主要就是要想清楚如何统计的末尾0个数
因为:
而末尾的0显然由2*5得到,而一个阶乘运算中,2要比5多得多,所以只需要统计这个n的阶乘能提供多少个5就可以了
最后注意,像25是能提供两个5的,因为25=5*5,这也是为什么题目中会有0解的存在
而对于非0解,那答案就是5,因为至少要5个数之后才会在遇到一个带因子5的数,末尾0个数才会改变。
最后,我们先写一个函数计算末尾0个数,然后二分查找一下有没有f(x)刚好是k,如果没有就返0,有就返回5
class Solution
{private long zeroCount(long n){long zero=0;while(n>0){zero=zero+n/5;n=n/5;}return zero;}public int preimageSizeFZF(int k){long left=0,right=(long)5*k,mid;while(left<=right){mid=(left+right)/2;long c=this.zeroCount(mid);if(c>k)right=mid-1;else if(c<k)left=mid+1;elsereturn 5;}return 0;}
}相关文章:
LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * ... * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k,找出返回能满足 f(x) …...
maven打包顺序与jvm类加载顺序
背景:一次dev测试过程中,发现代码中关于jsr303的校验失效,校验类如下,会报一个莫名其妙的运行时错误;遂进行排查。import javax.validation.constraints.NotBlank;Data Accessors(chain true) public class Demo {Not…...

④ 链表
24. 两两交换链表中的节点 题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/ 注意点: 遍历链表的时候什么时候截止(避免空指针异常或无限死循环的问题)? 节点数量为偶数或链表为空时,cur.ne…...
小孩扁桃体肿大3度能自愈吗?6岁小孩扁桃体肥大怎么治效果好?
12月7日,四川眉山市民唐先生说,他刚出生的儿子在妇产医院分娩中心住了20天后感染了败血症。据唐先生介绍,哈子出院时各项指标正常。他在分娩中心住了半个月左右,孩子喝牛奶很生气,第二天就开始发烧了。同一天ÿ…...
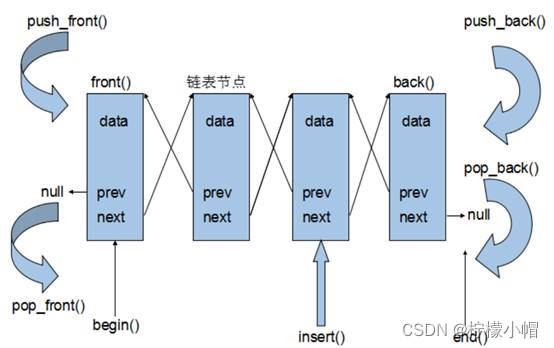
【C++提高编程】C++全栈体系(二十二)
C提高编程 第三章 STL - 常用容器 五、stack容器 1. stack 基本概念 概念:stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口 栈中只有顶端的元素才可以被外界使用,因此栈不允许有遍历行为 栈中进入数据称为 — 入…...
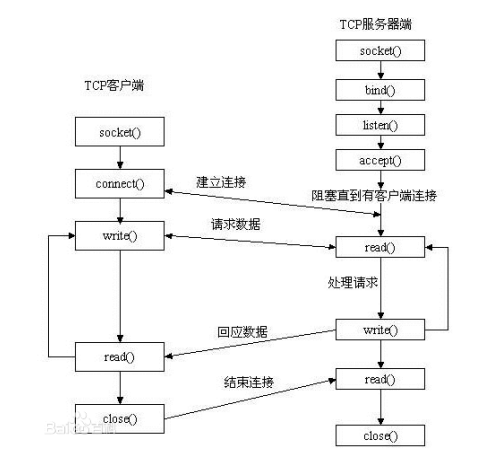
linux系统编程2--网络编程socket知识
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...
、join()、yield()和append()函数)
Python-__repr__、__hash__和__eq__方法,split()、join()、yield()和append()函数
1.__repr__方法程序1class Python:passa Python() print(a) print(a.__repr__())结果<__main__.Python object at 0x0000023B82185FD0> <__main__.Python object at 0x0000023B82185FD0>默认情况下,我们得到的信息只会是“类名object at内存地址”程序…...
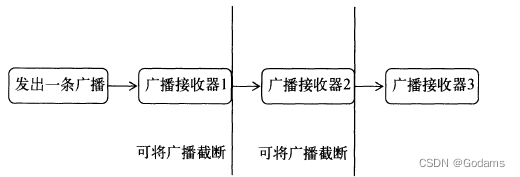
【安卓开发】安卓广播机制
读书笔记系列(第一行代码) 5.1 广播机制简介 标准广播:完全异步执行,广播发出后,所有广播接收器几乎都同一时刻收到这条广播(无法被截断)有序广播:同步执行,广播发出后…...
移动WEB开发四、rem布局
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...
和request.getURI() 以及通过request获得路径相关大全)
request.getURL()和request.getURI() 以及通过request获得路径相关大全
request.getURL()和request.getURI() 如果我的请求是:http://localhost:8080/ServletTest/servlet/Hello request.getRequestURI() 返回值类似:/ServletTest/servlet/Hello request.getRequestURL() 返回值类似:http://localhost:8080/Servle…...
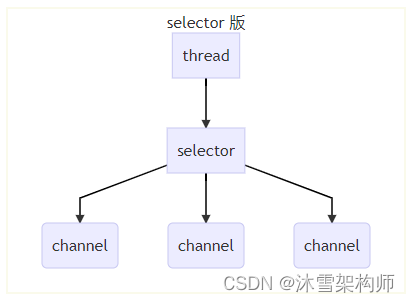
java网络编程-nio学习:阻塞和非阻塞
一、阻塞 阻塞模式下,相关方法都会导致线程暂停 ServerSocketChannel.accept 会在没有连接建立时让线程暂停 SocketChannel.read 会在没有数据可读时让线程暂停 阻塞的表现其实就是线程暂停了,暂停期间不会占用 cpu,但线程相当于闲置 单线…...
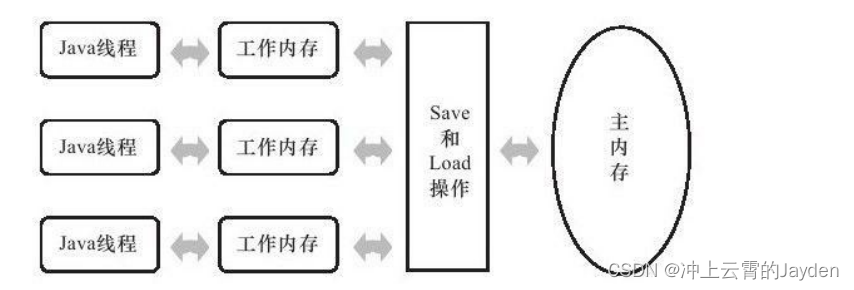
JVM-JMM内存模型(happens-before、volatile)
前言 由于计算机的存储设备与处理器的运算速度有几个数量级的差距所以现代计算机系统都不得不加入一层读写速度尽可能接近处理器运算速度的高速缓存(Cache)来作为内存与处理器之间的缓冲。 将运算需要使用到的数据复制到缓存中,让运算能快速进行,当运算…...

算法leetcode|37. 解数独(rust重拳出击)
文章目录37. 解数独:样例 1:提示:分析:题解:rustgoccpythonjava37. 解数独: 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现…...
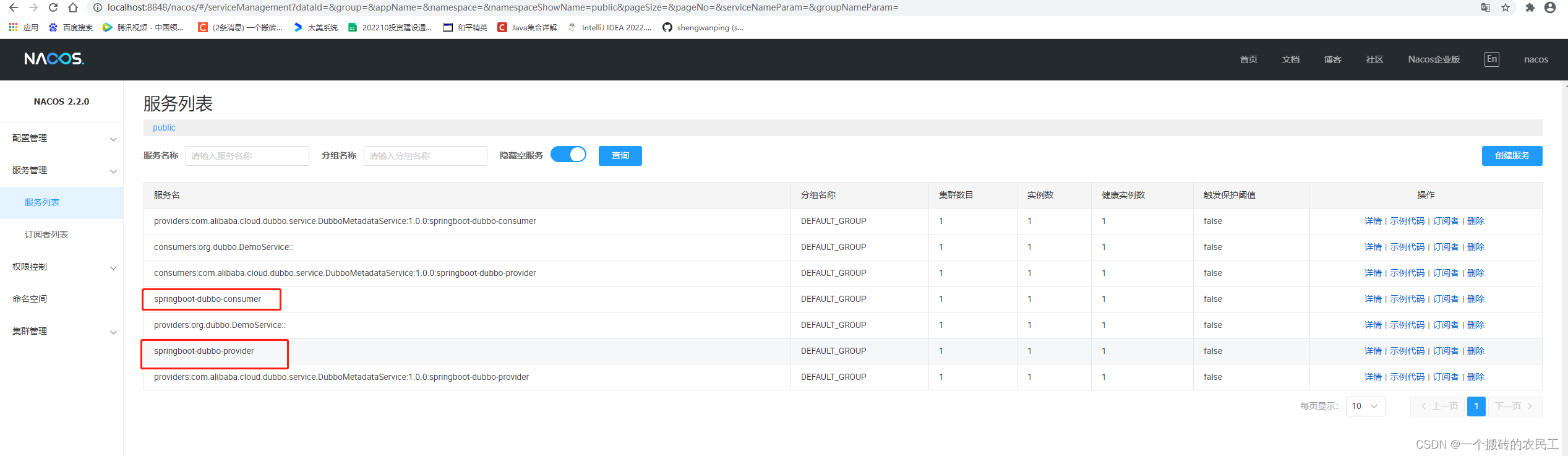
SpringBoot整合Dubbo
目录1、dubbo简介2、dubbo解决了什么问题3、环境准备4、项目搭建5、总结springboot整合feign可参考我另外一篇文章SpringBoot集成Feign 1、dubbo简介 Apache Dubbo 最初在 2008 年由 Alibaba 捐献开源,很快成为了国内开源服务框架选型的事实标准框架 ,…...
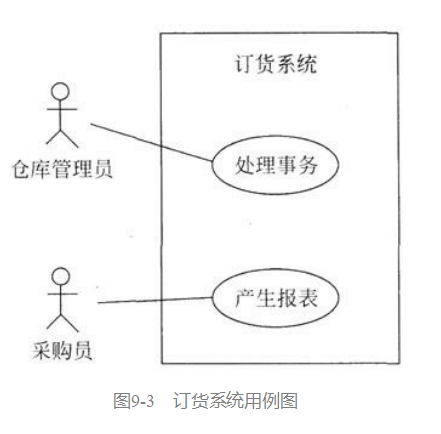
[软件工程导论(第六版)]第9章 面向对象方法学引论(课后习题详解)
文章目录1. 什么是面向对象方法学?它有哪些优点?2. 什么是“对象”?它与传统的数据有何异同?3. 什么是“类”?4. 什么是“继承”?5. 什么是模型?开发软件为何要建模?6. 什么是对象模…...

光学分辨率光声显微镜中基于深度学习的运动校正算法
在这项研究中,我们提出了一种基于深度学习的方法来校正光学分辨率光声显微镜 (OR-PAM) 中的运动伪影。该方法是一种卷积神经网络,它从具有运动伪影的输入原始数据建立端到端映射,以输出校正后的图像。首先,我们进行了仿真研究&…...

浅谈UG二次开发中使用的FindObject
一般我们在业务逻辑里想查找一个Object的时候,会调用FindObject、GetObject、NxObjectManager.Get,不管是上述哪种实现,都是在内存中找东西,找到了就返回对象,否则返回null,但不会触发加载。 这里我分别从建…...

贪心原理及刷题
更新中 概念 使用贪心需要满足,上一步的局部最优解能推出这一步的局部最优解,直到得到全局最优解 而dp这一步的局部最优,不一定来源上一步的局部最优,而可能与更早的解有关,同时dp转移方程的推导也比较复杂 122. 买卖股票的最佳时机 II - 力扣(LeetCode) 这道题是典…...
2023赏金计划:Coremail SRC漏洞征集与样本奖励火热进行中
赏金活动一:Coremail SRC漏洞奖励计划 01 活动背景 2023年1月,Coremail安全应急响应中心(Coremail SRC)正式上线启用,面向公众收集安全漏洞信息与安全情报。Coremail SRC旨在联合众多安全专家、白帽子研究员共同发现…...
简记:清理指定后缀名文件的 powerhsell 小脚本
清理指定后缀名文件的 powerhsell 小脚本jcLee95:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/129121074 1.介绍 相关工具代码 2.目…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
